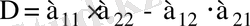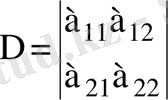Матрицалар теориясы және сызықты теңдеулерді шешу әдістері


Кіріспе
Математика - нақты өмірдегі сандық қатынастар мен кеңістіктік формалар туралы ғылым. Математикада математикалық модельдер зерттеледі. Ол нақты құбылыстардың тура математикалық модельдері болуымен қатар осы модельдерді зерттеуге арналған (структуралар) объект болуы мүмкін. Бір математикалық модель тура мазмұны жағынан бір-бірінен қашық жатқан нақты құбылыстардың қасиеттерін көрсетуі мүмкін. Мысалы, бір дифференциалдық теңдеу халықтың өсу процессін де жəне макроэкономикалық динамикасын да көрсетеді. Математика үшін қарастырылып отырған объектілердің табиғи мəні емес, олардың арасындағы қатынастардың маңызы зор. Математика жаратылыс ғылымдарында, инженер-техникалық жəне гуманитарлық зерттеулерде маңызды роль атқарады. Ол көптеген білім бөлімдерінде тек қана сандық есептеу жасау үшін ғана емес, сонымен қатар дəлірек зерттеудің тəсілі жəне ұғымдар мен проблемалардың шекті тура тұжырымдарын беру құралы болады. Адам өміріндегі əртүрлі салалардағы прогресс жетілдірілген логикалық жəне есептеу аппараты бар қазіргі замандағы математикасыз мүмкін емес. Математика қолданбалы есептерді шешуге арналған күшті құрал жəне ғылымның əмбебап тілі ғана емес, сонымен қатар ол негізгі мəдениеттің элементі де болып есептеледі. Сондықтанда математикалық білім осы заманға экономистерді фундаментальды дайындау жүйесіндегі маңызды бөлім болады.
1. Матрица
Математикада кез келген жиынның элементтерінен құрылған және m жол мен n бағаннан тұратын тік төртбұрышты А кестесі. Матрицаны түзетін нысандар оның элементтері деп аталады. Матрицаның элементтері оның жолдары немесе бағаналарының бойымен орналасады. Матрицаның элементтері а іj түрінде қос индекспен өрнектеледі, мұндағы бірінші индекс і - Матрицаның аіj элементі орналасқан жолының нөмірін, екінші индекс j - оның аіj элементі орналасқан бағананың нөмірінкөрсетеді. Матрица символдық түрде не дөңгелек жақша, не қос тік сызық арқылы өрнектеледі. Мұндай матрицаны (m n) өлшемді тікбұрышты матрица деп, ал егер m=n болса, квадрат матрица деп, n санын оның реті деп атайды.
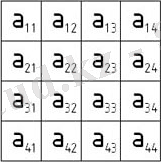
(1-сурет) Матрица
Матрицаны қысқаша былай белгілейді: (а іj ) . Жолдарының саны мен бағаналары санының бірі немесе екеуі де шексіз болатын матрицаны шексіз матрица деп түсінеміз. Бір ғана жолдан немесе бір ғана бағанадан тұратын матрицалар да болады. аіі диагональ элементтері ғана нөлден өзгеше болатын квадрат матрицаны диагональ М. деп аталып, dіag(а 1 … а n ) таңбасымен белгіленеді. Диагональ матрицаның барлық элементтері (а і =1) болса, бірлік матрица деп аталады. Егер барлық (а і =а) болса, онда скаляр матрица шығады. Барлық элементтері нөлге тең М. нөлдік М. деп аталады. Жолдары мен бағаналарын ауыстыру арқылы алынған матрица транспозицияланған матрица деп аталып, А немесе АТ арқылы белгіленеді. Егер матрицаның элементтерін комплекс түйіндеске ауыстырсақ, онда комплекс түйіндес матрицасы шығады. Егер А транспозицияланған матрица элементтерін комплекс түйіндеске ауыстырсақ, онда А матрицамен түйіндес болатын А* матрицасышығады. Квадрат матрицаның анықтауышы A немесе det A деп белгіленеді.

(2-сурет) Ұзындықтары бірдей
 жолдан тұратын сандардың тік бұрышты кестесін матрица деп атайды.
жолдан тұратын сандардың тік бұрышты кестесін матрица деп атайды.
2. Матрицаларға қолданылатын амалдар
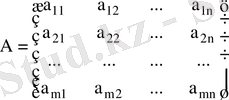
1) Матрицаларды қосу : Тең ретті
 және
және
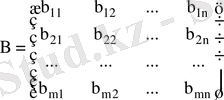
матрицалары берілген. Қысқаша, бұл матрицаларды
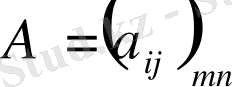 ,
,
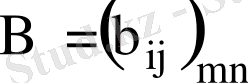 деп белгілейміз. Мұндағы
деп белгілейміз. Мұндағы
 -матрицаның жатық,
-матрицаның жатық,
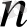 -тік жолдарының саны.
-тік жолдарының саны.
А және В матрицаларының қосындысы деп, элементтері
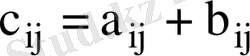 ,
,
 формулалары бойынша есептелетін
формулалары бойынша есептелетін
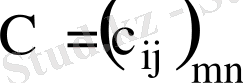 матрицаны айтамыз. Сонымен,
матрицаны айтамыз. Сонымен,

2) Матрицаларды санға көбейту
:
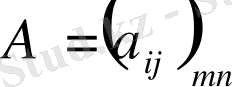 матрицасының
матрицасының
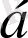 санына көбейтіндісі деп, элементтері
санына көбейтіндісі деп, элементтері
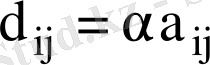 ,
,

формулалары арқылы анықталатын
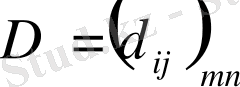 матрицасын айтамыз. Сонымен,
матрицасын айтамыз. Сонымен,
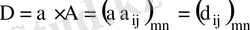 .
.
3) Матрицаны матрицаға көбейту:
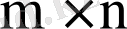 ретті
ретті
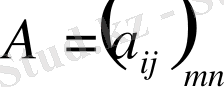 және
және
 ретті
ретті
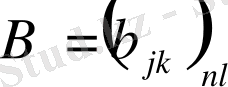 матрицалары берілсін. А матрицасының В матрицасына көбейтіндісі деп элементтері
матрицалары берілсін. А матрицасының В матрицасына көбейтіндісі деп элементтері
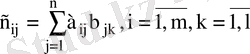
формулалары бойынша анықталатын,
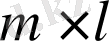 ретті
ретті
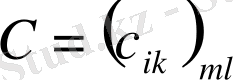 матрицасын айтамыз. Сонымен,
матрицасын айтамыз. Сонымен,
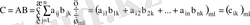 .
.
4) Матрицаны транспонирлеу: Матрицаның жатық жолдарын, орналасу ретін сақтап, тік жолдарымен алмастыру матрицаны транспонирлеу деп аталады. Егер

болса, онда

транспонирленген матрица болады.
Матрицаны элементар түрлендіру
Мынандай түрлендірулер матрицаны элементар түрлендіру болып табылады.
Матрицаның кез келген екі жолының (бағанының) орнын ауыстыру
Матрицаның кез келген жолын (бағанын) нольден өзгеше санға көбейту (бөлу)
Матрицаның кез келген жолының (бағанының) элементтерін бір санға көбейтіп (бөліп) басқа бір жолдың (бағанның) сәйкес элементтеріне қосуға болады.
Егер В матрицасы А матрицасын элементар түрлендіру арқылы алынса, онда оларды эквивалентті матрицалар деп атап,
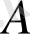 ~
~
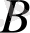 түрінде белгілейді.
түрінде белгілейді.
Элементар түрлендірулер арқылы кез келген матрицаны бас диагоналінің қатарынан бірнеше элементі бір, қалған элементтері ноль болатын матрицаға келтіруге болады. Мұндай матрицаны канондық матрица деп атайды.
2. 1. Кері матрица
Квадратты матрица
.
Жатық жолдар саны тік жолдар санына тең
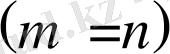 матрица квадратты деп аталады.
матрица квадратты деп аталады.
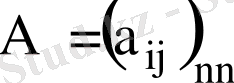 квадратты матрицасы берілген.
квадратты матрицасы берілген.
Егер
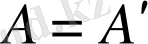 , демек
, демек
 болса, онда А симметриялы матрица деп аталады.
болса, онда А симметриялы матрица деп аталады.
Квадратты А матрицаның анықтауышын
 деп белгілейміз. Әлбетте,
деп белгілейміз. Әлбетте,
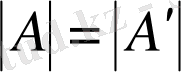 . Анықтауышы нөлге тең матрица ерекше деп аталады.
. Анықтауышы нөлге тең матрица ерекше деп аталады.
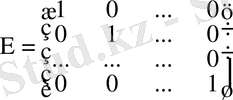
бірлік матрица деп аталады.
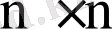 ретті
А
және
В
матрицалары берілсін. Егер В матрицасы үшін
ретті
А
және
В
матрицалары берілсін. Егер В матрицасы үшін
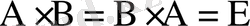 (4)
(4)
теңдігі орындалса, онда В матрицасы А-ға кері матрица деп аталады да
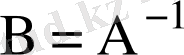 деп белгіленеді. Осы белгі арқылы (4) теңдігі
деп белгіленеді. Осы белгі арқылы (4) теңдігі
 түрінде жазылады.
түрінде жазылады.
Егер А ерекше матрица болмаса, демек
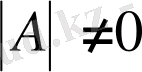 болса, онда А-ға кері бірден-бір матрица бар болады және кері матрица
болса, онда А-ға кері бірден-бір матрица бар болады және кері матрица
 (5)
(5)
формуласы бойынша анықталады.
Матрицаның рангісі:
Анықтама 6.
 жатық және
жатық және
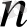 тік жолдардан тұратын
тік жолдардан тұратын

кестесі
 ретті матрица деп аталады. Әдетте, матрица бір бас әріппен белгіленеді, мысалы М деп.
ретті матрица деп аталады. Әдетте, матрица бір бас әріппен белгіленеді, мысалы М деп.
Осы матрицаның кез келген
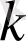 жатық және
жатық және
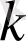 тік жолдарын белгілеп алып, осы жолдардың қиылысуындағы элементтерден, олардың берілген матрицадағы орналасу ретін сақтап құрылған
тік жолдарын белгілеп алып, осы жолдардың қиылысуындағы элементтерден, олардың берілген матрицадағы орналасу ретін сақтап құрылған
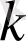 - ретті анықтауыш
- ретті анықтауыш
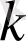 -
ретті минор деп аталады (
-
ретті минор деп аталады (
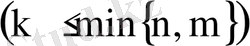 .
.
Егер М матрицасында нөлге тең емес
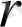 ретті минор бар болса, ал реттері
ретті минор бар болса, ал реттері
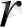 -ден жоғары барлық минорлар нөлге тең болса, онда
-ден жоғары барлық минорлар нөлге тең болса, онда
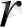 саны осы матрицаның рангі деп аталады және
саны осы матрицаның рангі деп аталады және
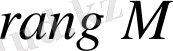 деп белгіленеді:
деп белгіленеді:
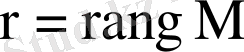 .
.
Барлық элементтері нөлге тең матрица нөлдік матрица деп аталады. Келісім бойынша, нөлдік матрицаның рангі нөлге тең.
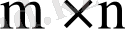 ретті, сәйкес элементтері өзара тең екі матрица тең матрицалар деп аталады.
ретті, сәйкес элементтері өзара тең екі матрица тең матрицалар деп аталады.
Рангті есептеу әдістері: 1) Көмкерген минорлар әдісі. Берілген матрицаның
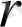 -ретті минорының көмкеруі деп осы минор енетін кез келген
-ретті минорының көмкеруі деп осы минор енетін кез келген
 ретті минорын айтады.
ретті минорын айтады.
Теорема 1 Егер берілген М матрицасының нөлге тең емес
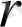 -ретті миноры бар болса және осы минорды көмкеретін барлық
-ретті миноры бар болса және осы минорды көмкеретін барлық
 ретті минорлар нөлге тең болса, онда бұл матрицаның рангі
ретті минорлар нөлге тең болса, онда бұл матрицаның рангі
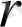 -ге тең:
-ге тең:
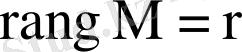 .
.
2) Рангті берілген матрицаның элементтерін түрлендіру арқылы есептеу. Бұл әдіс төмендегі теоремаларға негізделген.
1) Жатық жолдардың орнын алмастыру;
2) Кез келген жатық жолын нөлге тең емес санға көбейту;
3) Кез келген жатық жолына осы матрицаның басқа жатық жолын бір санға көбейтіп қосу;
4) Бірыңғай нөлден тұратын жолын алып тастау, матрицаның рангін өзгертпейді.
Бас диагоналы астындағы элементтері нөлге тең матрица сатылы деп аталады. Квадратты матрицаның сатылы түрі үшбұрышты деп аталады.
Теорема 3 Сатылы түрге келтірілген матрицаның рангі оның бас диагонолындағы нөлге тең емес элементтерінің санына тең.
Сызықты теңдеулер жүйесі
белгісізі бар
теңдеулер жүйесі мына түрде беріледі:
(6)
Мұндағы
- белгісіз шамалар,
-
нөмерлі теңдеудегі
нөмерлі белгісіздің коэффициенті,
-
нөмерлі теңдеудің бос мүшесі,
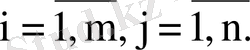
(6) теңдеулер жүйесінің коэффициентерінен құрылған мына матрица

(7)
негізгі матрица деп аталады, ал мына матрица
(8)
осы жүйенің кеңейтілген матрицасы делінеді.
Егер (6) теңдеулер жүйесінің барлық бос мүшелері нөлге тең болса, онда бұл жүйе біртекті деп аталады.
1. 2 пунктініњ 2-ші және 3-ші анықтамаларда аталған теңдеулер жүйесінің шешімі үйлесімді, үйлесімсіз, анықталған және анықталмаған теңдеулер жүйесі туралы ұғымдар өздерінің мағыналарын толық сақтайды.
(6) теңдеулер жүйесінің белгісіздері мен бос мүшелерінен
және
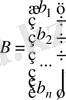
матрицаларын құрып осы жүйені мына матрицалық теңдеу түрінде жазамыз:
. (9)
белгісізі бар
теңдеулер жүйесін шешу әдістері
1) Крамер әдісі: Біртекті емес
белгісізді
теңдеулер жүйесі берілсін:
(10)
Осы жүйенің негізгі матрицасының анықтауышы

нөлге тең болмасын.
Осы анықтауыштың
нөмерлі тік жолының элементтерін (10) жүйесінің сәйкес бос мүшелерімен алмастырғанда шыққан анықтауышты
деп белгілеік:
,
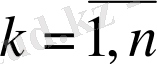
Осы анықтауыштар бойынша (10) теңдеулер жүйесінің шешімі Крамер формулалары арқылы анықталады:
.
2) Гаусс әдісі Гаусс әдісі матрицаның рангін өзгертпейтін элементар түрлендірулерге негізделген. Бұл түрлендірулер теңдеулер жүйелерінің эквиваленттігін сақтайды. Шешімдері бірдей немесе екеуі де үйлесімсіз болатын теңдеулер жүйелері эквивалентті деп аталады.
Гаусс әдісінің сұлбасы: Алдымен (10) теңдеулер жүйесінің кеңейтілген матрицасы құралады:

Элементар түрлендірулер арқылы бұл матрица үшбұрышты түрге келтіріледі:
(11)
Элементар түрлендірулердің қасиеті бойынша, (11) теңдеулер жүйесі (10) жүйесіне эквивалентті. (11) жүйесінің ең соңғы теңдеуінен
-ді, бір қадам жоғары көтеріліп, келесі теңдеуден
-ді табамыз. Осылай табылған
белгісіздерінің мәндері (10) жүйесінің шешімі болады.
Ескерту: (10) теңдеулер жүйесіне қойылған негізгі шарт осы жүйенің анықталғандығы, демек жүйенің анықтауышы
болуы. Сондықтан,
. Бұл шарт матрицалар әдісінде де сақталады.
3) Матрица әдісі. (10) теңдеулер жүйесін матрицалық түрде жазамыз
. (9 теңдеуі)
(5) формуласы бойынша А матрицасына кері
матрицасын табамыз. Енді (9) теңдеуін сол жағынан
-ге көбейтіп және
екенін ескеріп,
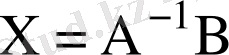
түрінде (9) теңдеуінің шешімін табамыз.
белгісізі бар
теңдеулер жүйесін зерттеу және үйлесімді болған жағдайда шешімін табу әдісі
Кронекер-Капелли теоремасы. Біртекті емес (6) сызықты теңдеулер жүйесі үйлесімді болу үшін осы жүйенің негізгі матрицасының рангі оның кеңейтілген матрицасының рангіне тең болуы:
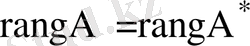
қажетті және жеткілікті.Бұл теорема арқылы жүйенің үйлесімді немесе үйлесімсіз болатыны шешіледі.
Жүйе үйлесімді болған жағдайда төмендегі екі жағдай қарастырылады:
1)
,
- белгісіздер саны,
. Бұл жағдайда теңдеулер жүйесі үйлесімді және анықталған. Сондықтан жүйенің шешімі жоғарыда аталған үш әдістің біреуі арқылы анықталады.
2)
,
- белгісіздер саны,
. Бұл жағдайда теңдеулер жүйесі үйлесімді және анықталмаған. А матрицасының кез келген
-ретті нөлге тең емес минорын негізгі деп жариялап, осы минордың элементтері коэффициенттері болатын
белгісізді негізгі белгісіздер деп аламыз. Мысалы, негізгі минор:

болса, негізгі белгісіздер
болады. Қалған
белгісіздер еркін параметрлер рөлін атқарып, теңдеулер жүйесі мына түрде жазылады:
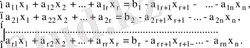
Бұл жүйеден Крамер, Гаусс, матрица әдістерінің біреуін қолданып
белгісіздерін табамыз. Белгісіздердің мәні
еркін параметрлерден тәуелді болады.
Әдістемелік нұсқау.
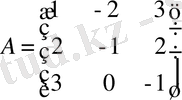 Табу керек
Табу керек
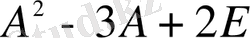
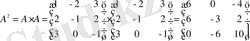
3
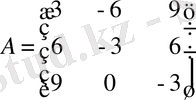 ;
;
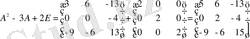
3. Анықтауыштар
Екінші ретті анықтауыш деп
санын айтамыз. Бұл сан екі тік және екі жатық жолдардан тұратын
кестесі түрінде белгіленеді және бұл кесте де анықтауыш деп аталады.
Мұндағы
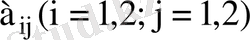 - анықтауыштың элементтері.
- анықтауыштың элементтері.
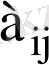 элементінің бірінші і индексі анықтауыштың жатық жолының, ал екінші j индексі тік жолының нөмері. Мысалы
элементінің бірінші і индексі анықтауыштың жатық жолының, ал екінші j индексі тік жолының нөмері. Мысалы
 - 1-жатық 2 - тік жолының қиылысуындағы элемент. Кестенің
- 1-жатық 2 - тік жолының қиылысуындағы элемент. Кестенің
 және
және
 элементтері арқылы өтетін «түзу» анықтауыштың негізгі диагоналы, ал
элементтері арқылы өтетін «түзу» анықтауыштың негізгі диагоналы, ал
 және
және
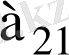 элементтері арқылы өтетін «түзу» қосалқы диагоналы деп аталады.
элементтері арқылы өтетін «түзу» қосалқы диагоналы деп аталады.
Анықтама бойынша, екінші ретті анықтауыш өзін белгілейтін кестенің негізгі диагоналындағы элементтерінің көбейтіндісі мен қосалқы диагоналындағы элементтері көбейтіндісінің айырымына тең. Демек,
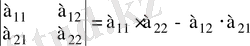
Анықтама: Үшінші ретті анықтауыш деп
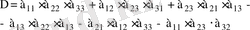
санын айтамыз. Бұл сан үш тік және үш жатық жолдардан тұратын
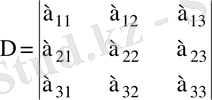
кестесі ретінде белгіленеді және бұл кесте де анықтауыш деп аталады. Мұндағы
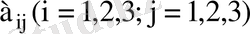 - анықтауыштың элементтері,
і -
жатық, ал
j
- тік жолдарының нөмірі.
- анықтауыштың элементтері,
і -
жатық, ал
j
- тік жолдарының нөмірі.
Үшінші ретті анықтауыш өзін белгілейтін кесте элементтерінен үшбұрыш немесе Саррюс ережесі бойынша есептеледі. Бұл ереже бойынша плюс таңбасымен алынған үш қосылғыш төменде келтірілген «+» сұлба, ал минус таңбасымен алынған үш қосылғыш «-» сұлба бойынша есептеледі:
«+» сұлба «-» сұлба
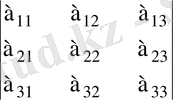
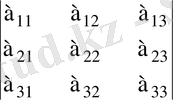
2. n-ретті анықтауыштар және оның қасиеттері
1-ден
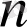 -
ге дейінгі натурал сандардың кез келген орналасуы алмастыру деп аталады.
-
ге дейінгі натурал сандардың кез келген орналасуы алмастыру деп аталады.
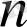 натурал саннан
натурал саннан
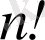 алмастыру қуруға болады. Егер алмастыруда үлкен сан кіші санның алдында тұрса, онда бұл сандар инверсия (ретсіздік) құрайды.
алмастыру қуруға болады. Егер алмастыруда үлкен сан кіші санның алдында тұрса, онда бұл сандар инверсия (ретсіздік) құрайды.
Егер
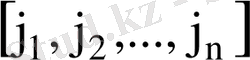 алмастыру болса, онда осы алмастырудағы инверсия саны
алмастыру болса, онда осы алмастырудағы инверсия саны
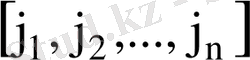 деп белгіленеді. Егер инверсия саны жұп болса алмастыру жұп, ал тақ болса тақ деп аталады.
деп белгіленеді. Егер инверсия саны жұп болса алмастыру жұп, ал тақ болса тақ деп аталады.
Анықтама 3.
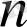 - ретті анықтауыш деп
- ретті анықтауыш деп
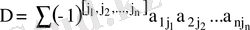
қосындыны айтамыз және оны былай белгілейміз
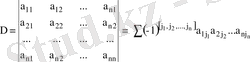 (1)
(1)
Мұндағы қосу белгісі 1, 2, 3, . . . ,
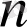 сандарынан құралған барлық
сандарынан құралған барлық
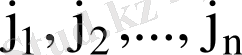 алмастырулары бойынша алынады, демек анықтауышта
алмастырулары бойынша алынады, демек анықтауышта
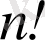 қосылғыш бар, олардың жартысы «+», жартысы «-» таңбасымен алынады.
қосылғыш бар, олардың жартысы «+», жартысы «-» таңбасымен алынады.
Анықтауышты белгілейтін кесте де анықтауыш деп аталады. Бұл кесте
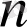 тік және
тік және
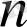 жатық жолдардан тұрады. Кестенің
жатық жолдардан тұрады. Кестенің
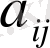 элементінің бірінші
элементінің бірінші
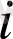 индексі -жатық, ал екінші
индексі -жатық, ал екінші
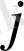 индексі тік жолының номері,
индексі тік жолының номері,
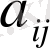 - осы жолдардың қиылысуындағы элемент.
- осы жолдардың қиылысуындағы элемент.
Егер анықтауыштың екі жатық (тік) жолының сәйкес элементтері өзара тең болса бұл жолдар тең деп аталады.
Егер анықтауыштың екі жатық (тік) жолдары өзара пропорционал элементтерден тұрса, демек
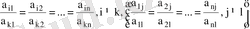
теңдігі орындалса, бұл жолдар пропорционал деп аталады.
Жатық (тік) жолдың
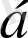 санына көбейтіндісі деп барлық элементтері
санына көбейтіндісі деп барлық элементтері
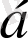 санына көбейтілген осы жолды айтамыз.
санына көбейтілген осы жолды айтамыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz