Сызықты жүйенің моделі

Кіріспе

Басқару тапсырмасында әрқашанда екі нысан болады - басқарылатын және басқаратын. Басқарылатын нысанды әдетте басқарудың нысаны немесе жай ғана нысан, ал басқаратын нысан - реттегіш деп аталады. Әдетте, реттегіш басқару нысанына тура емес, басқару сигналын күшейте немесе түрлендіре алатын атқарушы механизмдер ( жетектер ) арқылы әсер етеді. Реттегіш нысанмен не болып жатқанын «көре алу» үшін датчиктер қажет. Датчиктердің көмегімен көбінесе нысанның басқарылуы қажет сипаттамалары өлшенеді. Сонымен қатар, басқару сапасын жақсартуға болады, егер қосымша ақпарат алынса - нысанның ішкі қасиеттерін өлшеу.

Осылайша, басқарудың әдеттегі жүйесіне нысан, реттегіш, жетек және датчиктер жатады. Алайда, бұл элементтердің жинағы жүйе болып табылмайды. Жүйеге айналдыру үшін байланыс каналдары қажет, олар арқылы элементтер арасында ақпаратпен алмасу жүреді. Ақпараттарды жіберу үшін электр тоғы, ауа (пневматикалық жүйелер), сұйықтық(гидравликалық жүйелер), компьютерлік желілер қолданылуы мүмкін. Өзара байланысты элементтер - бұл, жеке элементтерде және олардың кез келген комбинацияларында жоқ ерекше қасиеттерге ие (байланыстың арқасында) жүйе.

Реттегішке қойылған мақсатты орындауға «кедергі» келтіретін, нысанға қоршаған ортаның - сыртқы әсерлер әрекет ететінін ескеру керек. Көптеген әсерлер алдын ала болжанбаған, яғни кездейсоқ сипаттамаға ие. Сонымен қатар, датчиктер параметрлерді аз болса да қандай да бір қателікпен тура есептемейді. Бұндай жағдайда «өлшеу шулары» жайлы айтылады.

Басқару жүйесінің міндеттері

Автоматические системы управления применяются для решения трех типов задач:

1. Тұрақтандыру, яғни ұзақ уақыт бойы өзгермейтін берілген уақыт режимін қамтамасыз етуто(мысалға, турбинаның айналу жиілігін реттеу жүйелерісистемы) .
2. Бағдарламалық басқару- алдын ала белгілі бағдарлама бойынша басқару (мысалға, пештегі қыздыру температурасының өзгеру бағдарламасы) .
3. Белгісіз берілген сигналдыбақылау(сигналдарды күшейту және түрлендіру үшін қажет, жетектеде және байланыс желілері арқылы командаларды жіберу кезінде қолданылады) .

№1 Зертханалық жұмыс
Сызықты динамикалық модельдерді зерттеу

Жұмыстың мақсаты

Автоматты басқару жүйелерінің (АБЖ) динамикалық және жиіліктік сипаттамаларымен танысу және сызықты динамикалық модельдерді зерттеу дағдысын алу.

Есептің берілуі

Зерттеу объектісі ретінде бір кірісті және бір шығысты сызықты динамикалық стационар басқару жүйелері алынады. Бір өлшемді АБЖ моделі полиномдардың қатынасы ретінде жазылған комплексті беріліс функциясы түрінде беріледі.

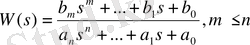(3. 1)

Жұмыстың реті:

1. tf функциясы көмегімен lti-объектқұру.
2. () .
3. Логарифмді және сызықты амплитудалы және фазалы жиіліктік сипаттамаларын құру.
4. Амплитудалы-фазалық сипаттамасын құру.
5. Жүйенің сатылы және импульстік кіріс сигналына әсерін анықтау және сәйкесінше өтпелі үрдістердің графигін салу.

Кесте 1.

Тапсырманың нұсқалары

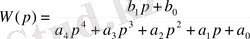
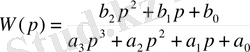
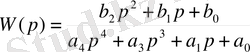
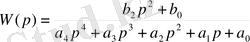
Жұмыстың есеп беруі

Есеп беру ЖОО-дағы жұмыстарды жасауға қойылатын талаптарға сәйкес орындалады, және келесідегідей мазмұны болу керек:

1. Негізгі бет

2. Жұмыстың атауы және мақсаты.

3. Жұмысты орындаудағы нәтижелері.

4. Нәтижелерді талдау және қорытынды.

Бақылау сұрақтары

1. Беріліс функциясы дегеніміз не?
2. tf функциясы көмегімен lti-объектті қалай құрамыз.
3. Функцияның полюстері мен нөлдеріне анықтама беру.
4. Амплитудалы және фазалық жиіліктік сипаттама деп нені айтамыз.
5. Амплитудалы-фазалық жиіліктік сипаттама дегеніміз не.
6. Өтпелі және импульстік өтпелі функция дегеніміз не? Сәйкесінше өтпелі үрдістердің графиктерін қалай құрамыз.

№2 зертханалық жұмыс.

Типтік динамикалық буындардың қасиеттерін зерттеу

Жұмыстың мақсаты: автоматты басқару жүйесінде қолданылатын типтік динамикалық буындардың динамикалық және жиіліктік сипаттамаларын есептеу.

Есептің берілуі: Зерттеу нысаны ретінде 2-ші кестедегі буындар алынады.

Кесте 2.

Типтік динамикалық буындар

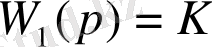
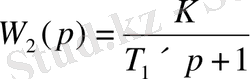
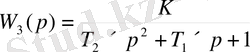
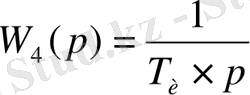
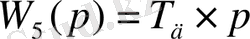
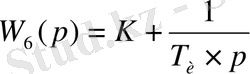
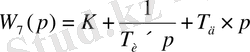
Жұмыстың есеп беруі:

1. Берілген буындардың логарифмдік және сызықты амплитудалық, фазалық және амплитуда-фазалық жиіліктік сипаттамаларын құру.
2. Жүйенің кіріске бірлік секіріс сигнал бергендегі әрекетін есептеу және сәйкес өтпелі үрдістердің графигін құру.

Кесте 3.

Тапсырма нұсқалары

Бақылау сұрақтары

1. Буындардың логарифмдік және сызықтық амплитудалық және фазалық жиіліктік сипаттамаларын қалай құрамыз.
2. Буынның амплитуда-фазалық сипаттамасын қалай құрамыз.
3. Берілген буындардың жиіліктік сипаттамаларын талдау.
4. Буындардың өтпелі сипаттамаларын талдау.

№3-4 Зертханалық жұмыс

Тұйықталған сызықты жүйені зерттеу

Сызықты жүйенің моделі

Сызықты жүйені сипаттаудың бірнеше жолдары бар:

• Дифференциалдық теңдеулер
• Кеңістік күйіндегі модель
• қосымша функция
• «нөлдер-полюстер» түріндегі модель

Алғашқы екі жолы уақытша деп аталады. Олар уақыт облысындағы жүйені сипаттайды және сигналдардың ішкі байланыстарын көрсетеді. Беріліс функциясы және «нөлдер-полюстер» модель түрі жиіліктік сипаттамаларға жатады. Себебі, олар жиіліктік сипаттамалар жүйесімен байланысты және тек сигналдардың кіріс-шығысын көрсетеді. Яғни динамикасын толық сипаттамайды.

Жиіліктік амалдар анализ бен синтезге алгебралық амалдарды қолдануға мүмкіндік береді, бұл есептеулерді оңайлатады. Басқа жағынан, автоматикалық есептеулерге кеңістіктік жағдайдағы модельдер одан да қолайлы. Себебі, олар сызықтық алгебрадағы тұрақты алгоритмді есептеулерді қолданады.

Физика заңының арқасында құрылатын динамика объектінің берілген есептеулері сызықты емес дифференциалдық есептеулер түрінде беріледі. Анализ бен синтезді тездету үшін орнатылған режимнің жан-жағына олардың линеаризациясын жүргізеді де, сызықты дифференциалды теңдеулерге ие болады.

Мына сызықтық теңдеуді 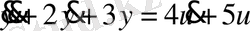мынадай операторлық формада жазуға болады

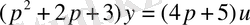немесе

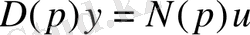
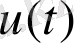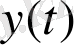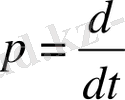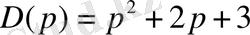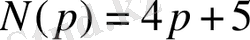Мұндағы - кіріс сигнал, - шығыс сигнал, - дифференциалау операторы, и - оператор полиномы.

Сызықтық стационарлы жүйенің беріліс функциясы 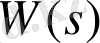коиплекстік ауыспалы 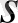қайта жаңару карым катынасы Лаплас кірісі мен Лаплас шығысының нөльдік бастапқы шарттарында анықталады

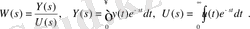
Жоғарыда келтірілген есептеулермен анықталатын звено беріліс функциясы мынаған тең

,

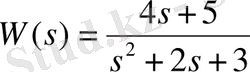Яғни, полиномның операторлық қатынасымен сәйкес келеді 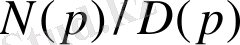, 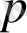-ның 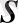-қа ауысуынан кейін.

Matlab ортасының беріліс функциясы s комплексті ауыспалының арқасында екі полиномның қатынасы ретінде енгізіледі. Полиномдар коэффициент массивы сияқты сақталынады. Мысалы, беріліс функциясы

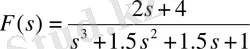
Келесідей енгізіледі

>> n = [2 4]

n =

2 4

>> d = [1 1. 5 1. 5 1]

d =

1. 1. 5000 1. 5000 1.

>> f = tf ( n, d )

Transfer function:

2 s + 4

s^3 + 1. 5 s^2 + 1. 5 s + 1

немесе сан мен ауыстырғышты құрмай ақ бірден енгізсе болады:

>> f = tf ( [2 4], [1 1. 5 1. 5 1] ) ;

Есінде беріліс функциясын анықтайтын tf класс объектісі құрылады . Команданың соңындағы үтір-нүкте оны экранға шығарады.

Беріліс функциясының көмегімен «нөлдер-полюстер» формасындағы моделді оңай құруға болады

>> f_zpk = zpk(f)

Zero/pole/gain:

2 (s+2)

(s+1) (s^2 + 0. 5s + 1)

Нөлдер деп сандардың түбірлерін атайды, полюстер - түбірдің орнын басушы. Бұл функция 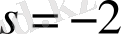нүктесінде бір нөл және 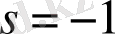нүктесінде үш полюсі бар

.

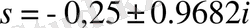Бұл полюстер комплексіне квадраттық үшмүше сәйкес келеді.

Кеңістік күйіндегі модель стандартты түрдегі Коши дифференциалдық есептеулерімен тығыз байланысты:

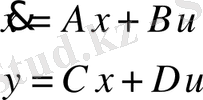
Бұл жерде ­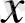- ауыспалы күйде өлшемі 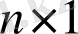болатын вектор, - кіріс сигналдар векторы (басқару векторы) 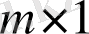өлшемді және де 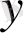-шығыс сигналдар векторы өлшемі 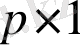. Сонымен қатар, 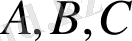және 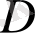- күнделікті матрица. Матрицалық есептеулерге байланысты, А матрицасы квадраттық өлшемде болуы керек, 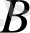матрицасының өлшемі ,

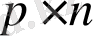матрицасы - өлшемді и 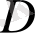матрицасы - өлшемді. Бір кірісі және бір шығысы бар матрица 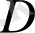- скаляр өлшемді болып табылады.

>> f_ss = ss ( f )

a =

x1 x2 x3

x1 -1. 5 -0. 1875 -0. 03125

x2 8 0 0

x3 0 4 0

b =

u1

x1 0. 5

x2 0

x3 0

c =

x1 x2 x3

y1 0 0. 5 0. 25

d =

u1

y1 0

Модель матрицасы мынадай түрде болады

, , , .

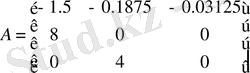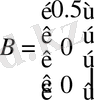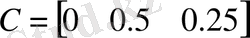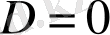Кеңістік күйдегі модельді барлық беріліс функциясы үшін емес тек ауыстыру өлшемі сандық өлшемнен улкенірек болатын дұрыс функция үшін қолданылады.

Мысалы, беріліс функциясы

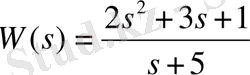
- дұрыс емес, ол кеңістік күйінде өзгеруі мүмкін емес.

Сонымен қатар қатаң дұрыс функцияны қолданады. Олардың сандық мәні ауыстырғыш мәнінен алдеқайда кіші болады.

Орнатылған режимдегі күшейткіш коэффициенті

Сызықтық жүйенің бірден-бір маңызды сипаттамаларының бірі ­- орнатылған режимдегі күшейткіш коэффициенті немесе статикалық күшейткіш коэффициенті ( static gain, DC-gain ) . Оны күнделікті шығыс сигналының мағынасы кіріс сигналда бірге тең болған кезде анықтауға болады. Бұның өлшемі кіріс және шығыс сигналдар өлшемімен тең.

Мына дифференциалды амалды қарастырайық

.

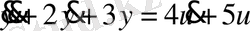Орнатылған режимде барлығы нөлге тең екенін ескере отырып мынадай амал аламыз

.

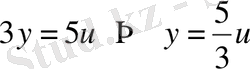Статикалық күшейткіш коэффициенті 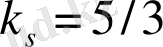тең.

Егер беріліс функциясы берілген болса, 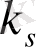-ні табу үшін оған 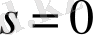қосып жазамыз, себебі ауыспалы 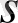дифференциалды операторға сәйкес келеді. Жоғарыда қарастырған есептеулерден мынадай беріліс функциясын аламыз

.

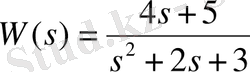Сонда

.

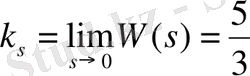Егер жүйеде интегралдайтын звено болған жағдайда, оның шегі шексіздікке тең болады, яғни күнделікті сигналда сигнал шығысы шексіз үлкейеді орнатылған режимге жете алмайды.

Дәл сондай шешімді кеңістік күйдегі эквивалентті моделден де алуға болады. Matlab ортасының көмегімен

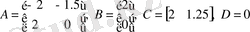табамыз .

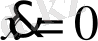біле отырып, орнатылған режимдегі моделді аламыз

,

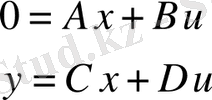
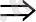
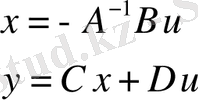
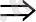
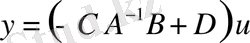Содан

.

f моделдің статикалық күшейту коэффициентін табу үшін Matlab ортасында келесі команда қолданылады

>> k = dcgain ( f )

Импульстік сипаттама

Импульстік сипаттама деп 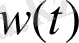жүйенің бірлік шектік импульсына рекциясын атаймыз, бастапқы нөлдік шарттарда. Дельта-функция 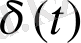мына теңдіктің көмегімен орындалады.

, .

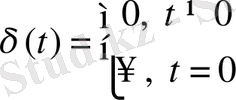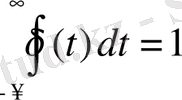Бұл біріктірілген функция - идеалды сигналды қарастыратын математикалық объект. Дельта-функцияны үшбұрыштық импульстің шектік мәні ретінде қарастыруға болады.

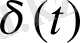
Екінші аты - салмақ функциясы - кіріс сигналы 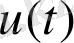вых шығыс сигналына 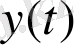айналуы

.

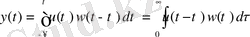Импульсттік сипаттамалар тек кіріс-шығыс қатынасының бастапқы нөлдік шарттардағы динамика жүйесін толық сипаттап береді.

Импульсттік сипаттама ұғымы тек қатаң дұрыс функциялар үшін қолданылады. Егер беріліс функциясы дұрыс болса, бірақ катаң дұрыс емес болса, кірістен шығысқа тікелей жіберу коэффициенті нөлге тең емес, сондықтан шексіз импульс кірісіндегі 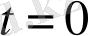моменті шығысқа жіберіледі. Мұндай импульстік сипаттамаларды салып тұрғызу мүмкін емес. Matlab жүйесі импульсттік сипаттамаларды өте қатаң есептерде қолданады, 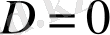-ді ала отырып. Бұл компьютердің дұрыс шешім бермейтін кездер.

Егер жүйеде интеграторлар болмаса, импулсттік сипаттама нөлге ұмтылады:

,

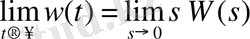Бұл жерде 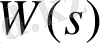- Жүйенің беріліс функциясы, Лапласа теңдеуінің 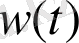үшін түрленуі болып табылады.

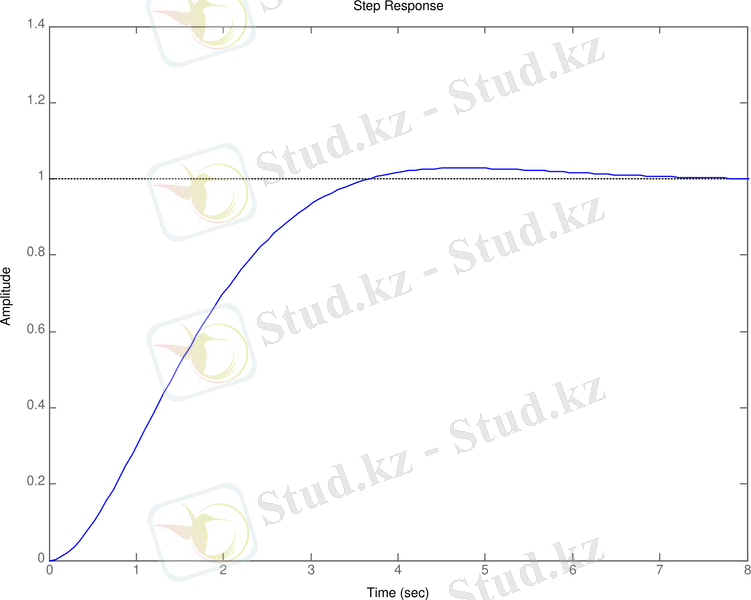
Беріліс сипаттамалары

Беріліс функциясы бұл жүйе реакциясы болып табылады.

.

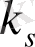
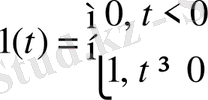Импульстттік және берілістік функциялар бір-бірімен осылайша байланысады

, .

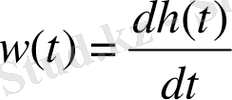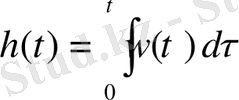Интеграторсыз жүйелерге беріліс функциясы күнделікті мағынасына ауысады. Дефференциалды звеносы бар беріліс коэффициентінің сипаттамасы нөлге ұмтылады. Егер де жүйе интегралдық звеносы болған жағдайда, беріліс функциясы асимптотикалық сипаттамамен тік беріледі немесе парабола және тағы басқалары, интегратордың санына байланысты.

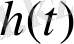
Анықтама бойынша беріліс функциясы болған жағдайда статикалық күшейткіш коэффициенті қолданылады:

.

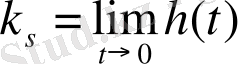Бұл өлшем тек тұрақты жүйелерге мағынасы бар болып табылады.

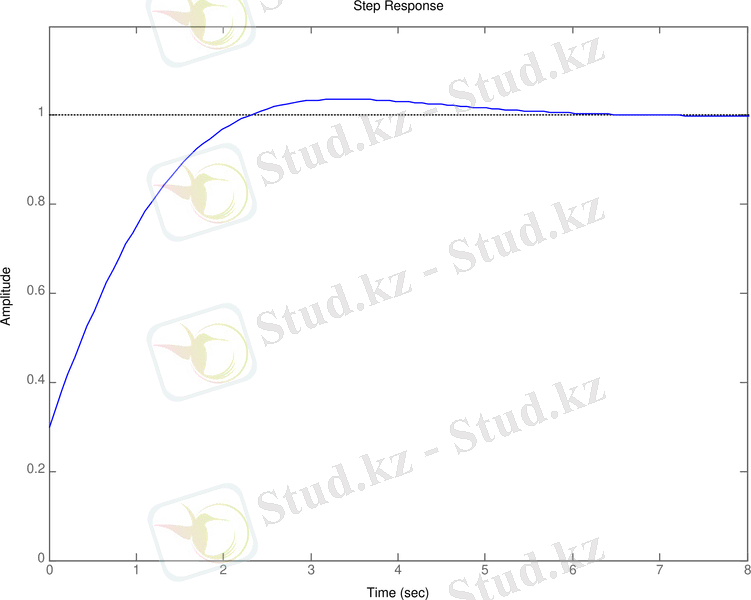Егер беріліс функциясы дұрыс болса, бирақ катаң дұрыс емес болса, модель матрицасы нөлге тең емес дегенді білдіреді. Интеграторсыз жүйелерге беріліс функциясы күнделікті мағынасына ауысады. Дефференциалды звеносы бар беріліс коэффициентінің сипаттамасы нөлге ұмтылады.

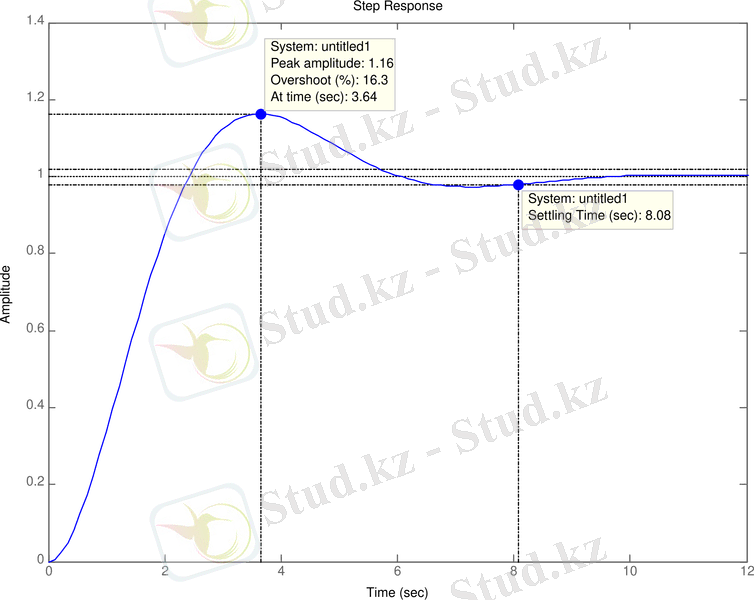Беріліс сипаттамаларына байланысты ең маңызды жүйе бағасының көрсеткішін табуға болады - қайта жасау ( overshoot ) және беріліс процесінің уақыты ( settling time ) .

Қайта жасау былай анықталады

,

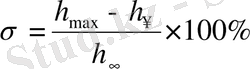Мұнда 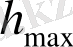- 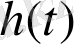функциясының максималды мағынасы, ал 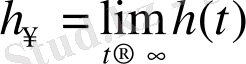- шығысының орнықтылған мәні.

Жиіліктік сипаттама

Сызықты жүйенің кірісіне гармоникалық сигналды жіберген кезде

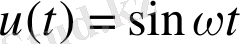
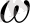жиілігімен шығысында да дәл сондай гармоникалық сигнал сондай жиілікпен боладыбірақ амплитудасы мен фазасы әр түрлі болады

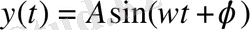
Мұндағы 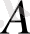- амплитуда және 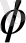- фазалар ауысуы.

Жиіліктік сипаттама жүйенің реакциясы ретінде қарастырылады, бұл жердегі экспоненциалды сигнал

.

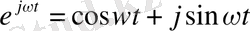Оны құру үшін мынадай құрылымды қарастырамыз 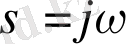, ал беріліс функциясында 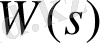. 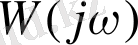деп жиіліктік беріліс функциясын атаймыз немесе амплитудалық-фазалық жүйенің жиіліктік сипаттамасы.

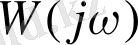модулі жиілікке байланысты болады. Ол амплитудалық-жиіліктік сипаттама деп аталады:

.

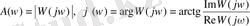АЧХ сигнал амплитудасыныңның жүйеден өткеннен кейін қаншалықты күшейетінін көрсетеді, ал ФЧХ фазалар ауысуының сигналын сипаттайды.

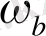
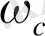
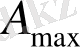
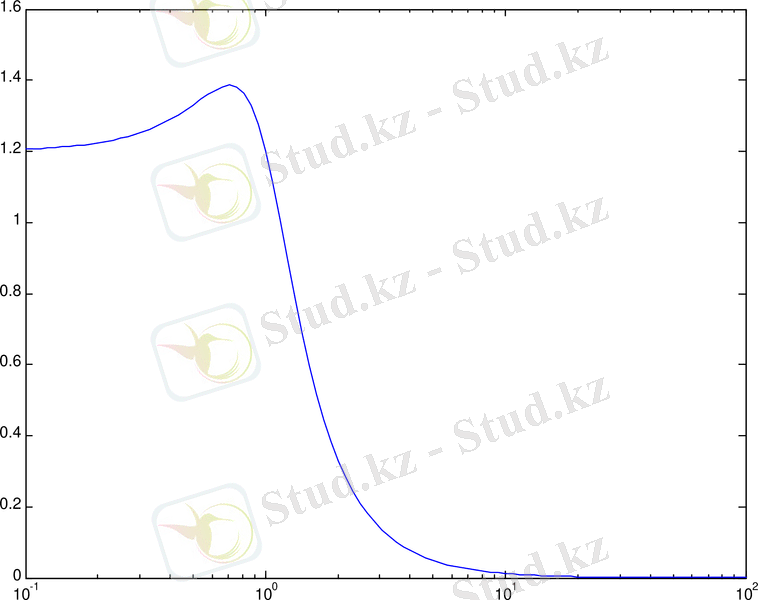
АЧХ -нің мағынасы 0дБ-ге дейін түскен кезде жиілік 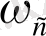жүйесінде сигналы бөліну жиілігі деп аталады. Ал АЧХ мағынасы -3дБ-ге дейін түсетін жиілік 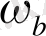жүйесінде Жіберу сызығы деп аталады. Оны есептеу үшін мынадай есептеуді қолданады

>> b = bandwidth ( f )

Одан кейінгі теңдеу

.

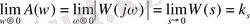Интегралданған звеносы бар жиіліктік сипаттамадағы жүйелер шексіздікке ұмтылады 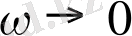. Бұл дегеніміз кіріс сигналында оның шығысы шексіз үлкейе береді.

Matlab ортасында жиіліктік сипаттамаларды құру үшін, Бірінші мезетте жиілік массивтерін керек диапазонда құрып алу керек. Бұл үшін linspace функциясын қолдануға болады және logspace командасы

>> w = linspace (0, 10, 100) ;

Массивті интервалы 0ден 10ға дейінгі 100нүктеден бірдей ретпен құру керек, командасы

>>w = logspace (-1, 2, 100) ;

- массив интервалы 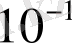до 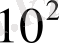болатын 100нүктеден тұратын бірдей ретпен.

Жиіліктік сипаттама сеткада w сызықты модель f үшінfreqresp функциясының көмегімен есептеледі :

>> r = freqresp(f, w) ;

Бір кірісі және бір шығысы бар жүйеге үшөлшемді массив құру оңайырақ бірдей командамен

>> r = r(:) ;

Matlab ортасында АЧХ графигін шығару үшін

>> plot ( w, abs(r) ) ;

>>semilogx ( w, abs(r) ) ;

>> loglog ( w, abs(r) ) ;

Бірінші жағдайда екі координаттың да сапасы-сызықты, екінші жағдайда логарифмдік масштаб абсцисса осімен, соңғы жағдайда екі осьтегі логарифмдік масштаб қолданылады. Фазаны есептеу үшін мына команда орындалады

>> phi = angle(r) *180/pi;

Одан кйін ФЧХ графигін салса болады, мысалы:

>> semilogx ( w, phi ) ;

Полюстер мен нөлдер

Жүйенің көптеген динамикалық сипаттамалары беріліс функциясының полюстерімен анықталады. Беріліс функциясын Бірінші және екінші реттегі беріліс функциясының звено ретімен жазуға болады. Бұл жол арқылы, Беріліс функциясының көптеген полюстері тұрақты жүйеде апериодты және тербелісті екі звено құрайды.

Апериодты звено беріліс функциясы мына күйде болған жағдайда 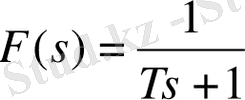бірден-бір сипаттамасы - тұрақты уақыты . Мынадай жиілікте бастаса 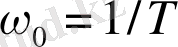, бұл звенодағы АЧХ нөлге ұмтылып төмен түседі.

Тербелмелі звено беріліс функциясы мына күйде болған жағдайда 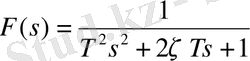, мұндағы - тұрақты уақыт және 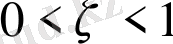. Жиілігі 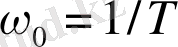жеке жиілік ( natural frequency ) деп аталады, ал мына параметр 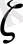- өшу параметрі немеседемпфирлау коэффициенті ( damping factor ) . Мына параметр төмендеген сайын 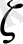импульстік және беріліс функциялары анық көрінеді, және 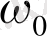жиілігінде АЧХ пайда болады.

Беріліс функциясының f полюстерін табу үшін мына функцияны қолдануға болады

>> p = pole ( f )

Функцияны шақыру

>> [w0, zeta, p] = damp ( f )

Бұл тек полюстерді p табу үшін ғана емес , сонымен қатар оған сәйкес жиілікті w0 және демпфирлау коэффициентін zeta массив түрінде табуға көмектеседі.

Беріліс функциясының f нөлдері былай есептеледі

>> z = zero ( f ) ;

Жүйенің тұрақтылығы нөлдердің орналасуына байланысты болады, және беріліс сипаттамаларына әсер етеді, мұндағы команда

>> pzmap ( f ) ;

Нөлдердің дұрыс орналасу картасын құрады.

Беріліс функциясын бірінші және екінші реттегі элементарлық звенолардың түрінде жазуға болады. Бұл жол арқылы, беріліс функциясының көптеген полюстері тұрақты жүйеде апериодты және тербелісті екі звено құрайды.

№ 3-4 Зертханалық жұмыс

Тұйықталған сызықты жүйені зерттеу

Жұмыстың мақсаты

• Matlab ортасының көмегімен біртекті сызықты үзіліссіз жүйені анализ шарттарын оқып-үйрену

Жұмыстың барысы

• беріліс функция түріндегі жүйенің моделін шығару
• кеңістік күйінде эквивалент моделін құру және және «нөлдер-полюстер» формасында
• орнатылған режимде күшейткіш коэффициентін
• импульстік және беріліс сипаттамаларын, нөлдер және полюстер картасын, жиіліктік сипаттамасын құрып үйрену
• әр түрлі сипаттамаларды құруда LTIViewer терезесін қолданып үйрену
• Сызықтық жүйенің шығысында процестер құру

Есеп беру

Бұл жұмыстың есеп беруі арнайы программа Microsoft Word-та орындалады. (шрифт Times New Roman , 12 пункт) . Оның ішінде

• Сабақтың аты, жұмыстың нөмірі мен аты
• Жазған адамның тегі мен аты, топ нөмірі
• Мұғалімнің аты тегі
• Нұсқа нөмірі
• Қысқаша сипаттама

Жұмысты орындау реті

Негізгі жұмысы Matlab ортасында жүзеге асады:

... жалғасы

Динамикалық хаос радиотехникалық генераторлардың негізінде нейрондық торды құру

Ақпараты толық емес техникалық жүйенің басқару заңын синтездеу

Математикалық модельдеудің кезеңдері

Математикалық модельдеу бойынша дәрістер

Автотербелмелі жүйелер кластерінің сигнал өндіру режимдері және оларға шуыл мен флуктуациялардың әсерін тәжірибе жүзінде зерттеу

Автоматты басқару теориясы

Дөңгелеу үйкеліс күші

Спиндік жүйелердің теориясы

Математикалық модельдерге қойылатын талаптар

Урбандалу процестерін моделдеудің ақпараттық жүйесін құру

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс