Көп электронды атомдар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 29 бет
Таңдаулыға:

Дәрістердің қысқаша конспектілері.

1 Дәріс. Электромагниттік сәуленің (жарықтың) кванттық (корпускалық) қасиеттері

Жылулық немесе температуралық сәуле шығару: қыздыру, яғни жылу беру салдарынан дененің сәуле шығаруы. Осылай шығарылған сәуле басқаша шығарылған барлық басқа сәуле түрлері арасында ерекше орын алады. Мұның басқаларынан айырмашылығы - бұл сәуле денелермен термодинамикалық тепе-теңдікте бола алатын сәуленің жалғыз түрі. Сондықтан да белгілі температурадағы денелермен тепе-теңдікте тұратын сәулені тепе-теңдіктегі сәуле шығару немесе қара сәуле шығару (черное излучение) деп атайды.

Тепе-теңдіктегі сәуле шығарудың ерекшелігі ол температураға ғана тәуелді болады. Сондықтан сәуленің өзінің температурасы жайында айтуға болады. Сонда сәуленің температурасы сәуле жылулық тепе-теңдікте тұрған денелердің температурасына тең деп есептеледі. Тепе-теңдіктегі сәуле біртекті, изотропты және поляризацияланбаған болады.

Кирхгоф заңы: кезкелген дененің 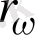сәуле шығарғыштық қабілетінің 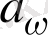сәуле жұтқыштық қабілетіне қатынасы жиілік пен температураның әмбебап функциясы болады:

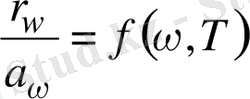(1. 1)

Кезкелген температура жағдайында кезкелген жиіліктегі барлық түсетін сәулені талғамай жұтуға қабілетті денені қара дене деп атайды. Қара дене үшін 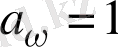. Сонда 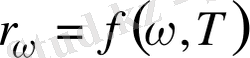. Демек, Кирхгофтың 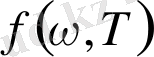әмбебап функциясы, физикалық мағынасы бойынша, ол қара дененің сәуле шығарғыштық қабілеті болады.

Қыздырылған дененің жылулық сәулесінің негізгі сипаттамасы:-дененің сәуле шығарғыштық қабілеті - дененің бірлік беті бірлік уақытта жиіліктердің бірлік аралығында шығаратын энергия мөлшері [Дж/м2] .
Тепе-теңдіктегі жылулық сәуленің негізгі сипаттамасы:

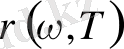-сәуленің спектрлік тығыздығы-бірлік көлемдегі жиіліктердің бірлік аралығына келетін сәуле энергиясы [Дж/м ³ ] .

Қара дененіңсәуле шығарғыштық қабілеті тепе-теңдіктегі жылулық сәуле шығару энергиясыныңспектрлік тығыздығымен мына қатынаспен байланысқан:

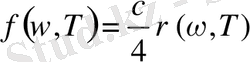(1. 2)

Жылулық сәуле шығару теориясының негізгі проблемасы осыфункцияны табуға тіреледі.

Осы проблеманы классикалық көріністер көмегімен шешуге істелген әрекеттердің бәрі сәтсіздікке ұшырады. Сәуле шығарушы дененің қарапайым мысалы - сызықтық гармоникалық осциллятормен жылулық сәуленің тепе-теңдікте болуы жайындағы есеп тантық нәтижеге алып келді. Жылулық сәуле шығару проблемасы осылай тұйыққа тірелді.

1900ж. Планк жылулық сәуленің спектрлік тығыздығы үшін эксперимент деректерімен жақсы үйлесетін формуланы тапты.

Қара дененің сәуле шығарғыштық қабілеті үшін Планк формуласы

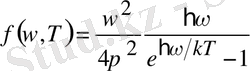. (1. 3)

Бірақта бұл үшін оған классикалық физика көріністеріне түбірінен қайшы жорамал енгізуіне тура келді. Планк осциллятор энергиясы кезкелген мән емес, тек қайсыбір элементар үлеске - 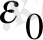энергия квантына пропорционал болатын белгілі дискретті 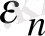мәндер қабылдай алады деген ұйғарым жасады. Осыған байланысты осциллятордың (заттың) электромагниттік сәулені шығаруы және жұтуы үздіксіз емес, шамасы сәуле шығару жиілігіне пропорционал жеке кванттар түрінде, дискретті іске асырылады; мұндағы -Планк тұрақтысы.

Планк тұрақтысы - әмбебап тұрақты, кванттық теорияда ол, салыстырмалылық теориясындағы жарық жылдамдығы сияқты, іргелі роль атқарады. Планк тұрақтысының және онымен байланысқан квантталу идеясының ашылуы жаңа, кванттық теорияның тууына бастау болды.

Сонымен, Планк жылулық сәуле шығару энергиясының спектрлік тығыздығы үшін формуланы, егер классикалық көріністерге қайшы келетін, энергия квантталады деп жорығанда ғана алуға болатынын дәлелдеді.

Жарық кванттары . Планктың кванттық гипотезасына сүйеніп жылулық сәуле шығарудан басқа да құбылыстарды түсіндіруге болатындығы анықталды.

1905ж. Эйнштейн жарық кванттары жайында жорамал ұсынды. Ол дискреттік қасиет жарықтың шығарылуы мен жұтылуы процестеріне ғана емес, жарықтың өзіне де тән деген ұйғарым жасады. Жарықтың корпускулалық қасиеттері жайындағы жорамал классикалық электромагниттік теория тұрғысынан тіпті түсініксіз болған фотоэффект бойынша тәжірибе нәтижелерін түсіндіруге мүмкіндік берді.

Осы жорамалға сәйкес түсетін монохроматты сәуле жарық кванттарының - фотондардың ағыны ретінде қарастырылады, бұлардың 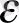энергиясы 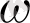жиілікпен мына қатынаспен байланысқан: 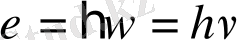. Фотон жұтылған кезде оның энергиясы бір электронға түгелдей беріледі. Сонымен осы жағдайда электрон кинетикалық энергияны біртіндеп емес, лезде қабылдайды. Электрон қабылдаған энергия ішінара оның металдан босап шығуына жұмсалады. Ал қалған бөлігі металдан ұшып шыққан фотоэлектронның кинетикалық энергиясына айналады. Электронды металдан босату үшін қажетті ең аз энергия, яғни потенциалдық тосқауылдан өтуі үшін қажетті энергия, А шығу жұмысы деп аталады. Демек, кинетикалық энергиясы ең үлкен К _max фотоэлектрондар үшін фотонның жұтылуының элементар актысындағы энергияның сақталу заңын былай жазуға болады (Фотоэффект үшін Эйнштейн теңдеуі) :

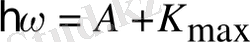(1. 4)

Тежеуілік рентген сәулесі . Егер квант энергиясы А шығу жұмысынан едәуір басым болса, онда (1. 4) Эйнштейн теңдеуі мына түрге келеді:

(1. 5)

Осы формуланы басқаша мағыналауға да болады: жарық кванты энергиясының электронның кинетикалық энергиясына айналуы ретінде емес, керісінше, U потенциалдар айырымымен үдетілген электрондардың кинетикалық энергиясының электрондардың металда шұғыл тежелуі кезінде пайда болатын кванттар энергиясына ауысуы ретінде қарастыру. Сонда

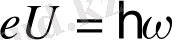(1. 6)

Дәл осындай процесс рентген түтікшесінде өтеді. Ол токпен қыздырылатын катоды (термоэлектрондар көзі) және оған қарама-қарсы орналастырылған аноды (антикатод деп аталатын) бар вакуумдық баллон. Электрондардың үдетілуі катод пен антикатод арасына түсірілетін U жоғары кернеумен іске асырылады.

U кернеудің әсерінен электрондар eU энергияға дейін үтетіледі. Металл антикатодқа түсіп, электрондар шұғыл тежеледі, осының салдарынан тежеулік рентген сәулесі деп аталатын сәуле пайда болады.

Толқын ұзындық бойынша жіктелгенде осы сәуленің спектрі, көрінетін ақ жарықтың спектрі сияқты, тұтас болып шығады. Және осы спектрдің қысқа толқынды шекарасы болатындығы тағайындалған (1. 1-сурет) . Классикалық элек-тромагниттік теория тұрғысы-нан қысқа толқындық шекара жалпы болмауы тиіс. Ал корпускулалық тұрғыдан қысқа толқындық шекараның болуы өте оңай түсіндіріледі. Шынында да, егер сәуле электрон тежелгенде оның жоғалтатын энергиясы есебі-нен пайда болатын болса, онда квант шамасы электронның eU энергиясынан үлкен болуы мүмкін емес. Осыдан сәуленің 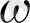жиілігі 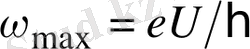мәнінен үлкен бола алмайды. Демек, шығарылған сәуленің толқын ұзындығы

1. 1-сурет

(1. 7)

мәнінен кіші бола алмайды (мұнда U, кВ, ал 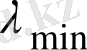, нм) .

Қысқа толқынды шекараның болуы рентген сәулесінің кванттық қасиеттерінің ең бір айқын білінуі болып табылады.

Комптон эффекті. Комптон фотонға энергия және импульс тән екендігін бақылауға болатын құбылыс ашты (1923) . Осы тәжірибенің нәтижелері - электромагниттік сәуленің өзінің кванттық табиғаты жайындағы Эйнштейн жорамалының тағы бір сенімді расталуы болды.

Комптон қатаң рентген сәулесінің жеңіл атомдардан тұратын графит, парафин сияқты және т. б. зат үлгілерінен шашырауын зерттеді.

Комптон шашыраған сәуле спектрінің құрамында толқын ұзындығы 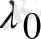бастапқы сызықтан басқа, толқын ұзындығы 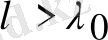, ығысқан сызық пайда болатынын байқады. Бұл комптондық ығысу деп, ал құбылысының өзі Комптон эффекті деп аталады.

Тәжірибе бақыланатын 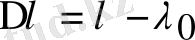комптондық ығысудың - шашыратушы зат үлгісінің материалына (затына) және түсетін сәуленің 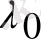толқын ұзындығына тәуелді болмайтындығын, тек шашыраған және бастапқы түсетін сәулелердің бағыттары арасындағы 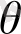бұрышпен анықталатындығын көрсетті:

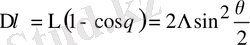, (1. 8)

мұндағы 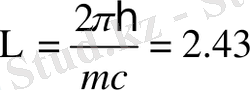пм - электронның комптондық толқын ұзындығы, т- электрон массасы.

Классикалық толқындық теория комптондық шашыраудың заңдылықтарын және ең алдымен ығысқан құраушының қалай пайда болатынын түсіндіруге жарамсыз болды. Теорияға сәйкес шашырау механизмі түсетін толқынның электромагниттік өрісінің электрондарды «тербеліске» түсіруімен түсіндіріледі. Осы жағдайда шашыраған сәуленің жиілігі түсетін сәуленің жиілігімен дәл келуі тиіс, яғни толқын ұзындығы өзгермеуі тиіс. Бұлар тек кванттық теория негізінде түсіндірілді.

Комптон рентген квантының толқын ұзындығы өзгеріп шашырауын оның электронмен жеке соқтығысу актысының нәтижесі ретінде қарастыру керек деп ұйғарды. Сонда Комптон эффекті тыныштықта тұрған еркін электронда фотонның серпімді шашырауы ретінде қарастырылады. Фотон электронмен соқтығысып, оған өзінің энергиясы мен импульсының бір бөлігін береді және қозғалыс бағытын өзгертеді (шашырайды) . Фотон энергиясының кемуі шашыраған сәуленің толқын ұзындығының өскендігін білдіреді.

Тәжірибеде қолданылған жеңіл заттарда электронның атоммен байланыс энергиясы рентген квантының (фотонның) электронмен соқтығысқанда оған электронға беретін энергиясымен салыстырғанда кіші болады. Бұл шашырау бұрышы неғұрлым үлкен болса, соғұрлым жақсы орындалады. Жеңіл атомдарда электронның байланыс энергиясын атом ішінде барлық шашырау бұрыштарында ескермеуге, яғни барлық электрондарды еркін деп санауға болады. Сонда 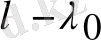комптондық ығысудың барлық заттар үшін бірдей болатындығы бірден түсінікті болады. Шынында да басынан бастап шашыратушы зат тек еркін электрондардан тұрады деп алынған болатын, яғни заттың жеке ерекшеліктері тіпті ескерілмеді. Бірақ бұл жеңіл атомдар үшін ғана дұрыс. Ауыр атомдардың ішкі электрондары үшін осындай көрініс жарамайды, мұны тәжірибе растайды.

Фотонның еркін электронмен соқтығысуын қарастырайық. Сонда энергияның және импульстың сақталу заңдары орындалуы тиіс екендігін ескереміз. Соқтығысу нәтижесінде электрон релятивті болып шығуы мүмкін. Сондықтан осы процесс релятивтік динамика негізінде қарастырылады.

1. 2 - сурет

Алғашында тыныштықта тұрған тыныштық энергиясы 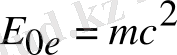еркін электронға энергиясы 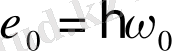және импульсы 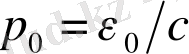фотон келіп соқтығысатын болсын. Соқтығысқаннан кейін фотонның энергиясы 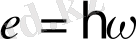, ал серпілген электронның энергиясы мен импульсы 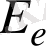және 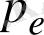болады. Фотон-электрон жүйесінің энергиясы мен импульсының сақталу заңдарына сәйкес соқтығысқанға дейін және соқтығысқаннан кейін мына теңдіктерді жазамыз:

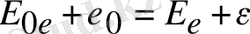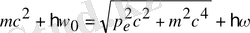; , (1. 9)

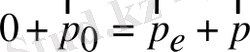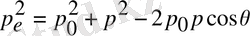; (1. 10)

Энергияның сақталу ( 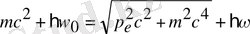) және импульстың сақталу

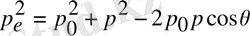( ) заңдарынан (косинустар теоремасын пайдаланып, 1. 2-суретті қара) 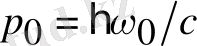; ; 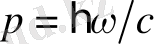; ; 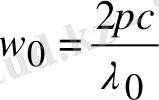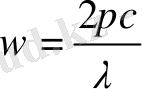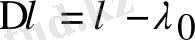формулалары ескерілгенде комптондық ығысу үшін (1. 8) формула алынады.

Шашыраған сәуледе ығыспаған сызықтың пайда болуына шашыратушы зат атомдарының ішкі электрондары себепші болады. Осы электрондардың байланыс знергиясы, әсіресе ауыр атомдағы, рентген фотондарының энергияларымен шамалас, демек, мұндай электрондарды енді еркін деп санауға болмайды. Осы жағдайда рентген фотоны атомның өзімен соқтығысып, онымен энергия және импульсымен алмасады. Ал атом массасы электрон массасынан өте үлкен болатындықтан, атомнан шашырағанда атомға фотон энергиясының болмашы аз бөлігі ғана беріледі. Сондықтан осы жағдайда шашыраған сәуленің λ толқын ұзындығы іс жүзінде түсетін сәуленің λ0толқын ұзындығымен бірдей болады.

2 Дәріс. Микробөлшектердің толқындық қасиеттері

Луи де Бройль (1924ж. ) фотондар ғана емес, электрондар да және материяның басқа бөлшектері де корпускулалық қасиеттермен қатар толқындық қасиеттерге де ие деген жорамал ұсынды. Яғни де Бройль корпускулалық-толқындық дуализм әмбебап сипатқа ие деген жорамал ұсынды. Әрбір микробөлшекпен бір жағынан, корпускулалық қасиеттер Е энергия және p импульс, ал екінші жағынан, толқындық қасиеттержиіліктолқын ұзындық, байланыстырылады.
Бөлшектердің корпускулалық және толқындық қасиеттерін сипаттайтын шамаларды байланыстыратын математикалық өрнектер дәл фотондардікі сияқты, яғни

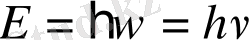және 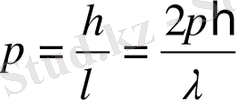(1. 14)

мұндағы Е-қозғалыстағы бөлшектің энергиясы; 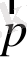- бөлшектің импульсы; 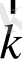-толқындық вектор; 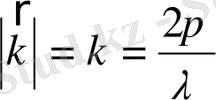; -Планк тұрақтысы.

Импульсыбөлшектің де бройлдық толқын ұзындығы

а) релятивтік емес жағдай

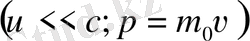
, (1. 15а)

б) релятивтік жағдай

[ , (1. 16а)

] (1. 16б)

(1. 15б)

Де Бройль толқын ұзындығының бөлшектің К кинетикалық энергиясымен байланысы:

а) релятивтік емес жағдай 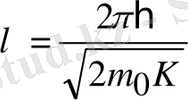; (1. 15в)

б) релятивтік жағдай 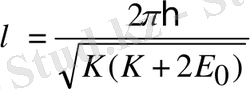; (1. 15г)

мұндағы Е ₀ -бөлшектің тыныштық энергиясы .

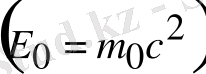Де Бройль жорамалы Дэвиссон және Джермер тәжірибелерінде расталды (1927) . Бұлардың тәжірибелерінің идеясы: егер электрондар шоғының толқындық қасиеттері болса, онда бұлардың кристалдан шағылуы, рентген сәулелерінікі сияқты, интерференциялық сипатта болуы тиіс, яғни осы жағдайда рентген сәулелерінің кристалдан шағылуына ұқсас интерференциялық шағылу максимумдары байқалуы тиіс. Кристалдың әр түрлі жазықтықтарынан, түскен сәуленің атомдардан дифракциялануы нәтижесінде, осы жазықтықтардан айналық шағылған сияқты болып, толқындар шығады. Осы толқындар интерферен-цияланғанда, егер Брэгг-Вульф шарты

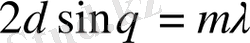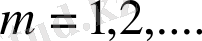, (1. 17)

орындалатын болса, онда бұлар бірін-бірі күшейтеді, мұндағы 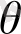-сырғу бұрышы, d-кристалдық жазықтықтардың арақашықтығы, Дебройлдық толқындардың кристалда сынуы ескерілгенде (1. 17) Брэг-Вульф формуласы мына түрге келеді:

(1. 17а)

Де Бройль толқындарының n сыну көрсеткіші

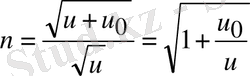(1. 17б)

мұндағы 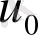-кристалдың ішкі потенциалы, -үдеткіш кернеу.

Анықталмағандықтар қатынастары:

а) координат пен импульс үшін , (1. 18а)

мұндағы - бөлшек координатының анықталмағандығы; 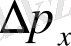- бөлшек импульсының тиісті координат осіне проекциясының анықталмағандығы;

б) энергия мен уақыт үшін 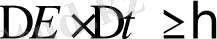, (1. 18б)

мұндағы -бөлшектің қайсыбір күйдегі энергиясының анықталмағандығы, 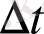- осы күйде болу уақыты.

3 Дәріс. Атомның ядролық моделі.

Атом оң зарядталған ядродан және оны қоршаған теріс зарядталған электрондардан (электрондық қабық) тұратындығы тағайындалған. Ядроның сызықтық мөлшері 10 ^-15 -10 ^-14 м шамасында. Атомның электрондық қабығымен анықталатын өзінің мөлшері бұдан 10 ⁵ еседей үлкен. Бірақ атомның түгелге дерлік массасы (99, 95 %) ядрода шоғырланған.

Атомның осы моделін α-бөлшектердің өте жұқа алтын фольгадан (қабыршақтан) шашырауы бойынша тәжірибе нәтижелеріне сүйеніп, Резерфорд (1911) ұсынған. Сондықтан ол Резерфорд моделі деп аталады.

Қозғалмайтын ядроның кулондық өрісінен зарядталған бөлшектің (α-бөлшек) шашырайтын θ-бұрышы

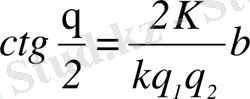немесе 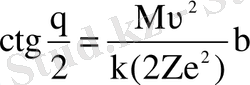(1. 1. 1)

формуласымен анықталады.

Мұндағы 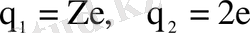- әсерлесетін бөлшектердің (ядро және α-бөлшек) зарядтары, 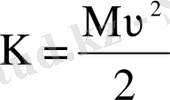- түсетін бөлшектің кинетикалық энергиясы, М - α-бөлшектің массасы, υ - оның ядродан алыстағы жылдамдығы, 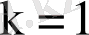(СГС), 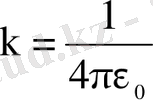(СИ) .

Атомдық құбылыстар аймағында тәжрибеде (1. 1. 1) формуланың өзін емес, осы формуланың статистикалық салдарын тексеруге болады. Осы жағдайда α-бөлшектің dΩ денелік бұрышқа шашырауы үшін ядроның дифференциалдық тиімді қимасы, шашыраудың толық қимасы ұғымдары енгізіледі.

- шашыраудың дифференциальдық тиімді қимасы деп атомнан (ядродан) уақыт бірлігінде dΩ денелік бұрышқа шашырағанбөлшектер санының түсетін бөлшектер ағынының І тығыздығына (І интенсивтігіне) қатынасын айтады; І - ағынға перпендикуляр бірлік аудан арқылы бірлік уақыт ішінде өтетін шоқтағы α-бөлшек саны.

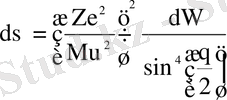, (1. 1. 2)

Мұндағы, 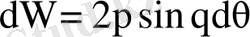- денелік бұрыш элементі. (1. 1. 2) формуламен Резерфордтың атомның ядролық моделін ұсынуына негіз болған эксперименттік деректер түсіндіріледі. (1. 1. 2) формула α-бөлшектердің бір ядродан шашырауын бейнелейді. Егер шашыратқыш фольгада ядроның тығыздығы n болса, онда олардың жалпы саны nV болады, мұнда, V - фольганың көлемі. Сонымен, шашыраған α-бөлшектер саны:

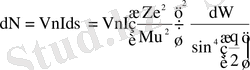(1. 1. 3)

формуламен анықталады.

Бөлшектердің бастапқы қозғалыс бағытына θ бұрышпен dΩ элементар денелік бұрышқа шашыраған бөлшектердің салыстырмалы саны үшін Резерфорд формуласы:

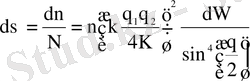, (1. 1. 4)

мұндағы n - фольга бетінің бірлік ауданына келетін ядро саны, К - фольгаға түсетін бөлшектердің (α-бөлшектер) кинетикалық энергиясы, 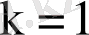(СГС) немесе 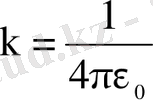(СИ), 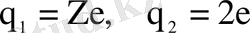- әсерлесетін бөлшектердің зарядтары.

Бальмердің жалпыланған формуласы

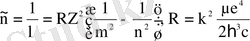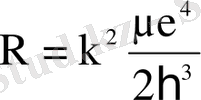(м ^-1 ), (с ^-1 ) (1. 1. 5)

қарапайым атом-сутегі атомының (z=1) және сутегі тәрізді иондар (z>1, He ⁺ , Li ⁺⁺ , …) спектрлеріндегі серияларды бейнелейді; 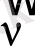- спектрдегі спектрлік сызықтардың толқындық саны; R - Ридберг тұрақтысы; m-серияны анықтайды (m=1, 2, …) ; n - тиісті серияның жеке сызықтарын анықтайды (n=m+1, m+2, …) .

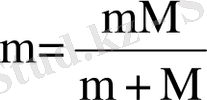жүйенің келтірілген массасы (m<<M болғанда μ≈m), z - ядро заряды.

R=3, 29⋅10 ¹⁵ c ^-1 , R=109677, 581 см ^-1 ; 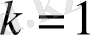(СГС) , 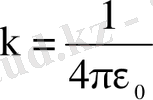(СИ) .

4 Дәріс. Сутегі атомының Бор ұсынған теориясы (1913) .

Н. Бор сутегі атомының бүкіл спектрін өте жақсы түсіндіретін және де атом құрылысының физикалық моделі негізіне алынған теория ұсынды. Бор моделіне сәйкес атомдағы электрондар ядроны орнықты (стационарлық) дөңгелек орбиталар бойынша айналып жүреді. Осы орбиталарға электронның белгілі энергиялары сәйкес келеді. Бір орбитадан екінші басқа орбитаға секіріп, электрондар энергияны қабылдап немесе жоғалта алады.

Бор теориясындасызықтық спектрлердің эмпирикалық заңдылықтары, Резерфордтың ядролық моделі және жарықтың шығарылуы және жұтылуының кванттық сипаты біртұтас біріктірілді.
Бордың бірінші постулаты. Атомда энергияның белгілі дискреттік мәндерімен сипатталатын стационарлық (уақыт бойынша өзгермейтін) күйлер болады, осы күйлерде ол энергия шығармайды.

Атомның стационарлық күйлеріне стационарлық орбиталар сәйкес келеді, осы орбиталар бойынша электрондар қозғалады. Стационар орбиталар бойынша электрондардың қозғалысы кезінде электромагниттік сәуле шығарылмайды. Атомның стационарлық күйінде, электрон дөңгелек орбита бойымен қозғалып,

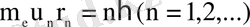(1. 1. 6)

шартын қанағаттандыратын, импульс моментінің дискретті квантталған мәндеріне ие болуы тиіс.

Бордың екінші постулаты. Электрон бір орбитадан басқасына ауысқанда энергиясы тиісті стационар күйлердің энергиялары айырымына тең

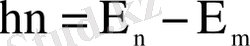(1. 1. 7)

бір энергия кванты - фотон шығарылады (жұтылады) .

Кванттық ауысулардың дискретті жиіліктерінің мүмкін болатын жиыны

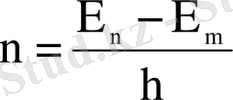(1. 1. 7 а)

атомның сызықтық спектрін анықтайды.

ni- стационарлық орбита радиусы:

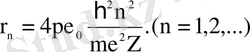. (1. 1. 8)

Бірінші Бор радиусы:

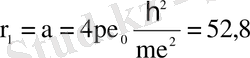пм. (1. 1. 8 а)

Сутегі тәрізді жүйедегі электронның толық знергиясы:

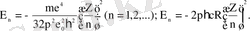(1. 1. 9)

Мұнда ядро (протон) массасы электрон массасынан ∞ ауыр (m<<M) деп алғанда Ридберг тұрақтысы

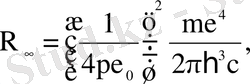м ^-1 (1. 1. 10)

былай өрнектеледі.

Ал М ядро массасының (протон) шектеулігі ескерілгенде m электрон массасын 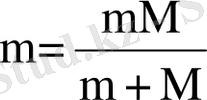келтірілген массаға ауыстыру керек. Сонда Ридберг тұрақтысы ядро массасына тәуелді болады:

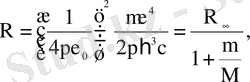м ^-1 . (1. 1. 11)

R Ридберг тұрақтысының ядро массасына тәуелділігі спектрлік сызықтардың изотоптық ығысуында білінеді:

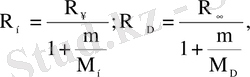(1. 1. 12)

Мұндағы, R _∞ =109737, 3534 см ^-1 , R _н =109677, 581 см ^-1 ,

R _D =109707, 419 см ^-1 .

Дейтерий сызықтары толқын ұзындықтарының сутегі сызықтары толқын ұзындықтарына салыстырғанда изотопты ығысуы

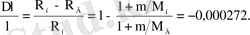
Мысалы, дейтерийдің D _α бальмер сызығы сутегінің Н _α сызығына қатысты қысқа толқынды аймаққа қарай 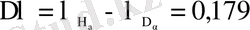нм аз шамаға ығысады. Бірақ осы ауытқу тәжрибеде айқын байқалады.

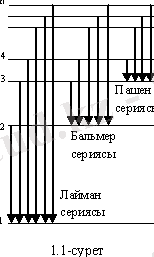
Сутегі атомы және сутегі тәрізді иондардың негізгі серияларының пайда болу (шығарылу) сызбасы (1. 1-сурет) .

5 Дәріс.

6 Дәріс. Бір электронды атомдық жүйелер

Бірэлектронды атомдық жүйеге ең алдымен өзара байланысқан протон мен электроннан тұратын-сутегі атомы жатады. Заряды +Ze ядродан және бір электроннан тұратын барлық иондар да: Не+(Z=2), Li++(Z=3), Be+++(Z=3) және т. т. бірэлектронды жүйелер болып табылады. Бейтарап сутегі атомы және сутегі тәрізді иондар - бір электроны бар ионданған атомдарбір электронды атомдардеп аталады. Бұлар изоэлектрондық қатар-электрон саны бірдей атомдар қатарын құрайды.
Бірэлектронды атом үшін Шредингер теңдеуін шешу. Бірэлектронды атом ядросымен координаттар басын сәйкестендіреміз. Ядроның кулондық өрісі координаттар басына қатысты сфералық симметриялы болатындықтан электронның қозғалысы жайындағы есепті шешу үшін,, сфералық координаттар жүйесі қолайлы болады. Электронның заряды Ze ядромен потенциалдық кулондық әсерлесу энергиясы мынаған тең:

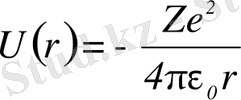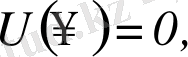, (1. 2. 1)

Мұндағы, r - электрон мен ядроның арақашықтығы.

Осы жағдайда электрон күйін бейнелейтін 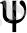-функцияны стационарлық күйлер үшін Шредингер теңдеуін

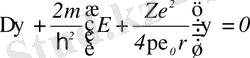(1. 2. 2)

шешу арқылы табуға болады, мұндағы, m - электрон массасы, Е - атомдағы электронның толық энергиясы, мұны 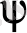-толқындық функция барлық қарастырылатын аймақта шектеулі, үздіксіз және бір мәнді болатын жағдайда табу керек. 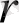, , координаттарында Лаплас операторы

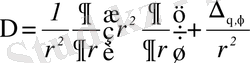, (1. 2. 3а)

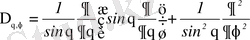(1. 2. 3б)

болып өрнектеледі.

(1. 2. 2) Шредингер теңдеуі

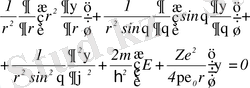(1. 2. 2а)

түріне келеді.

(1. 2. 2а) теңдеуі айнымалыларды бөлектеу әдісімен, ізделіп отырған 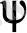-функция

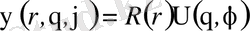(1. 2. 4)

деп ұйғарылып (яғни 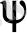-функция тек r -ге тәуелді R(r) радиалдық функция және тек θ мен φ -ге тәуелді Υ(θ, φ) бұрыштық (сфералық) функцияның көбейтісіндісі түрінде алынып) шешіледі.

Сонымен есеп (1. 2. 2а) теңдеуді шешуге саяды. (1. 2. 4) -ті (1. 2. 2а) -ға қойып алып және топтастырып, теңдіктің сол жағына радиалдық, ал оң жағына бұрыштық бөліктерін шығарып жазамыз:

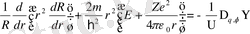
Осы теңдіктің сол және оң бөліктері әртүрлі тәуелсіз айнымалыларға тәуелді болатындықтан осы бөліктер жеке-жеке алғанда бір λ тұрақтыға тең болуы тиіс, сонда теңдік орындалады.

Сонымен R радиалдық функция үшін және Υ(θ, φ) сфералық функция үшін

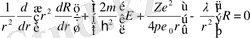
; (1. 2. 5)

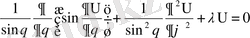
(1. 2. 6)

теңдеулерін аламыз.

(1. 2. 5) теңдеуі U(r) потенциалдық энергия түріне тәуелді. Сондықтан радиалдық функциялардың түрі және энергияның меншікті мәндері электрон қозғалатын өрістің нақты түрімен анықталады. (1. 2. 6) теңдеуі сфералық - симметриялық өріс түріне тәуелді емес. Осы теңдеудің шешімі барлық сфералық-симметриялық өрістер үшін бірдей болады. (1. 2. 6) теңдеуінің шешімінен λ айнымалыларды бөлектеу тұрақтысы λ = l(l+1) болатындығы келіп шығады. Дәл осылай бұрыштық бөліктің өзін екіге: тек θ полярлық бұрышқа тәуелді және тек φ азимуттық бұрышқа тәуелді бөліктерге ажыратамыз. Тағы да әрбір бөлік бір $m_{e}^{2}$ тұрақтыға теңестіріледі.