Симметриялық вибратордың кіріс кедергісі мен сәулелену сипаттамаларын инженерлік есептеу


М. О. Әуезов атындағы Оңтүстік Қазақстан Мемлекеттік Университеті
Кафедрасы АТ және Б
Реферат
Тақырыбы: Симметриялы вибратордың кіріс кедергісі
Орындаған : Досалы. Ж
Тобы: ИП15-7К1
Қабылдаған: Арыстанбаев. Қ
Шымкент, 2018
ЖоспарКіріспе3
Негізгі бөлім4
1. Симметриялық вибратордың кіріс кедергісі. Кіріс кедергінің инженерлі есептеу әдісі4
2. Симметриялық вибратордың сәулелену қуаты, сәулелену кедергісі және бағытталған әрекет коэффициенті7
Қорытынды10
Пайдаланылған әдебиеттер11
КіріспеАнтеннаның сәуле шығару қабілеті RS сәуле шығару кедергісі деп аталады. Бұл РS толық сәулелену қуатының антеннадағы ток квадратына қатынасы болып табылады. Егер де бұл сигналдың қуаты аз болса, онда ол сигналдың қуаты аз болса, онда сигналдың қуаты аз болса, онда ол сигналдың қуаты аз болса, онда сигналдың қуаты аз болады. Жақсы сәуле шығару қабілеті бар Антенна сол қуатты, бірақ нашар сәуле шығару қабілеті бар антеннаға қарағанда аз ток мәндерінде сәуле шығаруы мүмкін. Симметриялы вибраторға арналған RS есептеу формуласы күрделі және инженерлік есептеулер үшін аз жарамды. Бұл сфералық бет бойынша Пойнтинг векторының интегралдау күрделілігімен байланысты, бағыттылық диаграммасының квадратына пропорционалды Ішкі функция болған жағдайда да, салыстырмалы түрде қарапайым. Сондықтан іс жүзінде дайын есептеу нәтижесін пайдаланады. Симметриялы вибратордың кіріс кедергісі антенна кірісінде кернеу мен ток арқылы анықталады. Біз токтың таралу заңы мен кернеуді жоғалтумен ұзын сызықтардың теориясынан белгілі деп есептейміз, онда кіріс кедергісін есептеу үшін біз сол теорияны қолдануымыз керек. Жағдайда, симметриялық вибратордың белсенді жоғалту анықталады кедергісі сәулелену, ол тек қана ұзындығынан дірілдеткіштің және бос кеңістікте емес өзгертілуі мүмкін, егер электр ұзындығы антенна фиксирована және аз өзгереді. Сондықтан эквивалентті контурдың мейірімділігі тек сипаттамалық кедергі есебінен, яғни реактивті элементтер есебінен өзгертілуі мүмкін. Соңғы тікелей байланысты болса, толқындық кедергісі WВ және, демек, диаметрі сым вибраторлы. Қашан пайдалану қажет симметриялық butt, кең жиіліктер белдеуінде және қажет жатық, мүмкіндігінше аз өзгерту ZВХ (кіші беріктік), вибраторға жүгінеді айтарлықтай көлденең қимасы сым. Бұл ретте вибратор сымы дөңгелек және тұтас болуы міндетті емес, оны қуыс құбырдан немесе жазық таспадан немесе ұқсас торлы металл беттен орындауға болады.
Негізгі бөлім 1. Симметриялық вибратордың кіріс кедергісі. Кіріс кедергінің инженерлі есептеу әдісіГенератордан симметриялық вибраторға келген қуаттың бір бөлігі сәулеленеді. Ал қалған бөлігі вибратордың өзінде жоғалады, яғни оқшаулағышта (изолятор) және вибратордың айналасындағы заттарда. Сәулеленген қуат сәулеленудің активті кедергісіне сәйкес келеді. Қуат жоғалысы активті кедергі жоғалысына сәйкес келеді. Сәулеленгеннен басқа, антеннаның маңында тербелмелі, сонымен бірге реактивті қуатқа сәйкес келетін электрмагнитті өріс те бар. Бұл қуат кейде жақындағы өріске өтіп кетіп, генераторға беріледі, кейде кері өзіне қайтады. Көп жағдайда реактивті қуат антеннаның реактивті кедергісіне сәйкес келеді. Олай болса, антеннаға қосылған генератор антеннаның кіру кедергісі деп аталады. Кешенді (комплексный) кедергіге жүктелген және вибратордың қысқышындағы (зажим) кернеудің қоректендіру (питание) нүктесіндегі токқа қатынасына тең
. (1)
Кіру кедергісінің шамасы мен сипаттамасы антеннаға қосылған генератордың жұмыс режимін анықтайды. Көбінесе симметриялық вибраторда жоғалыс (потерь) аз, сондықтан деп шамалаймыз, мұндағы - қоректену нүктеде токқа жатқызылған вибратордың сәулелену кедергісі. Кіру кедергіні дәл анықтау үшін вибратордың бойындағы токтың таралу заңын білу қажет. Инженерлік мақсатта жеткілікті жиі жағдайда кіру кедергісі вибратор бойынша токтың таралу заңына жақын есептеледі. Кіру кедергісінің есептеу әдісіне жақынын қарастырайық. Вибратордың бойындағы ток синус заңы бойынша таралған деп, симметриялық вибратордың l/λ=0, 5 кіру кедергісін табамыз (сурет 1) .
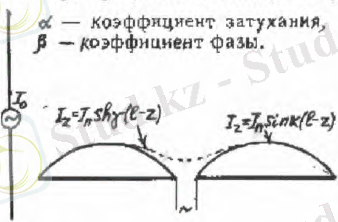
Сурет 1. «Қысқа» және «Ұзын» вибратор бойынша
токтың таралу
Бұл жағдайда қоректену нүктесіндегі ток нөлге тең болып шығады және екені анық. Шыныда да қоректену нүктесінде ток ешқашан нөлге тең болмайды және симметриялық вибратордың кіру нүктесі ешқашан шексіз үлкен болмайды. Бұл физикалық түрде әбден анық. Синус заңы желіде жоғалыс болмаған жағдайда ғана әділ ғой. Вибратор да сәулелену жоғалысы бар жүйе болып табылады. Кіру кедергісін есептегенде симметриялық вибратор мен ашық желінің соңындағы жоғалыс арасындағы ұқсастықты жүргізген жөн. Мұндай желідегі ток гиперболалық синус заңы бойынша таралғаны белгілі (сурет 1) .
, (2)
мұндағы: таралу коэффициенті; α - әлсіздену коэффициенті; β - фаза коэффициенті.
1-суретте көрініп тұрғандай ток таралуының айналым және гиперболалық синус заңдары бойынша тек салстырмалы ток буынынан (узел) жақын арақашықтықта елеулі айырмашылық аламыз. Сондықтан «қысқа» вибратордың (l/λ) ≤0, 35 . . . 0, 4; (0, 6 . . . 0, 65) ≤l/λ≤(0, 85 . . . 0, 9) кіру нүктесін есептегенде, яғни токтың буыны вибратордың қоректену нүктесіне (0, 1 . . . 0, 15) λ арақашықтықтан жақын емес орналасса, токтың синусоидальді таралуына шығып кетеді. «Ұзын» вибратордың (0, 35≤l/λ≤0, 65) кіру кедергісін есептегенде токтың гиперболалық синус заңы бойынша таралуынан шыққан жөн. «Қысқа» вибратордың активті және реактивті құрастырылған кіру кедергісін есептейтін формула табайық. Вибратормен сәулеленген қуатты шоғырдағы токтың амплитудасы ( ) арқылы білдіреміз және қоректену нүктесінде ( ) келесі формуланы аламыз:
және (3)
Формуланың сол жақ бөлігі өзара тең болғандықтан, болады. қатысты теңдікті шеше оытрып, аламыз.
орнына мәнін қоя отырып құрастырылған кіру кедергісін есептеуге арналған формуланы аламыз (вибратордағы жоғалысты есептемегенде) .
(4)
Вибратор үшін берілген ұзындықта шамасын кестеден немесе грфиктен табу оңай. Қысқа симметриялық вибратордың реактиті құрастырылған кіру кедергісін есептегенде жоғалыссыз екі өткізгіш желінің соңында алшақ тұрған кіру кедергісінің формуласы қолданылады және онда желінің толқындық кедергісі антеннаның толқындық кедергісімен ауыстырылады.
(5)
Олай болса, қысқа вибратордың толық кіру кедергісін келесі формулада анықтауға болады:
(6)
Вибратордың көлденең қимасының өлшемі кішірейген кезде (7) формула бойынша есептеу дәлдігі жоғарылайды. Ұзын вибратор жағдайында кіру кедергісі жоғалысқа ие желінің соңында алшақ тұрған екі өткізгіштің кіру кедергісіне ұқсас есептелінеді.
(7)
мұндағы: -вибратордың толқындық кедергісі; l-вибратор иілісінің ұзындығы; α-бәсеңдеу коэффициенті; β-вибратордағы фаза коэффициенті.
Вибратор өткізгішінде жоғалысты есептемегенде, ұзын желімен ұқсастығы бойынша бәсеңдеу коэффициентін мына формула бойынша есептеуге болады, мұндағы - вибратор ұзындығы бірлігіне елетін сәулеленудің активті кедергісі. Вибратордың барлық ұзындығы бойынша сәулелену біркелкі таралған деп, есептеу үшін келесі формуланы аламыз . Бұл формула сәулелену кедергісінің ток шоғырына (пучок) қатысты екенін біле тұра, сәулеленудің таралған кедергісін анықтауға мүмкіндік берді.
(8)
(8) формулада фаза коэффициенті β желідегі фазалық жылдамдық жоғалыспен және вибратордағы жарық жылдамдығынан біршама аз болғандықтан, бос кеістіктегі k фаза коэффициентімен біршама ерекшеленеді.
2. Симметриялық вибратордың сәулелену қуаты, сәулелену кедергісі және бағытталған әрекет коэффициентіСимметриялық вибратормен сәулеленетін электрмагнитті толқын қуатын элементар вибратор сияқты Пойтинг векторы әдісімен анықтауға болады. Осы әдіске сәйкес симметриялық вибратор сферамен қоршауға алынады. Оның радиусы r»λ, сол себепті сфераның беттік қабаты вибратор өрісінің ұзақ зонасында орналасқан. Вибратордың центрі сфераның центріне тура келеді, вибратордың осі тікбұрышты жүйедегі координат z осінде жатр. Сфераның беттік қабатында шексіз кішкентай элемент dS бөлініп шғады, ол - аудан координаттың сфералық жүйесінде . Осы элементтің беттік қабатына келетін сәулеленген қуат:
(9)
мұндағы: Е - dS элементінің кез келген нүктедегі электр өрісінің кернеулік амплитудасы (модуль), келесі мәнде анықталады:
(10)
Жалпы түрде бұл мән сәулелену кедергісі үшін келесідей болады:
(11)
.
шамасы ұзақ зонадағы электрмагнитті өрістің таралу сипаттамасымен анықталад, яғни қаралып жатқан антеннаның бағттылық диаграммасымен анықталады. Интегралдау 1924ж алғаш рет Баллантайн алған келесі формуланы береді.
. (12)
мұндағы: τ=0, 5772 . . . - Эйлер тұрақтысы; - интегральді синус; - интегральді косинус.
(12) Формулада көрініп тұрғандай, симметриялық вибратордың сәулелену кедергісі l/λ қатынасының шамасына тәуелді. (12) формула вибратор бойынша токтың синусоидальді таралуынаншыққан қорытындыға жақын болып табылады және тек жіңішке вибратор үшін әділ. Алайда (12) формула бойынша есептің нәтижесі экспериментпен тура келеді.
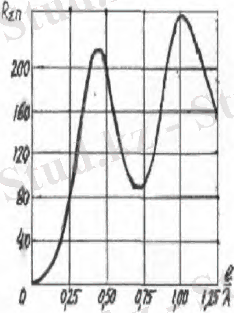
Сурет 2. - l/λ шамасынан тәуелділігі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz