Цилиндрлік координат жүйесіндегі dl тоқ элементінің магниттік моменті

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Жоспар

Кіріспе
Негізгі бөлім

2, 1 Диамагнетизмнің классикалық теориясы

2, 2 Диамагнетизмнің кванттық теориясы

2, 3 Заттардың магниттік қасиеттері. Парамагнетизм

Қорытынды
Пайдаланылған әдебиеттер

Кіріпсе

ҚАТТЫ ДЕНЕ - заттың агрегаттық күйі; пішінінің орнықтылығымен және атомдарының жылулық қозғалыс әсерінен тепе-теңдік қалпының маңында мардымсыз аз тербелістер жасайтындығымен сипатталады. Атомдарының орналасу сипатына қарай Қ. д-лер кристалдар және аморф денелерге бөлінеді. Кристалдар атомдары кеңістікте белгілі бір тәртіппен орналасады. Сондықтан оның қасиеттерінде кеңістіктік периодтылық байқалады. Аморфтық денелерде атомдар бей-берекет орналасқан нүктелердің төңірегінде тербеліп тұрады. Қ. д-лердің орнықты күйі (минималь ішкі энергиясы бар) кристалдық күй болып табылады. Ал аморф денелер, термодинамика тұрғысынан, әрқашан белгілі бір метастабильді күйде (уақытша тепе-тең) тұрады. Ол уақыт өткен сайын кристалдана бастайды. Табиғаттағы барлық заттар (сұйық гелийден басқасы) атмосф. қысым кезінде Т>0 К темп-рада қатаяды. Қ. д-лердің құрылымы қатаю процесінің өту ерекшелігіне, балқыманың құрылымы мен табиғатына байланысты анықталады. Қ. д. қасиеттерінің табиғатын кванттық теория негізінде ғана толық түсінуге болады. Кристалдардың кванттық теориясы аморф денелердің кванттық теориясына қарағанда толығырақ зерттелген. Қ. д. қасиеттерін оның атомдық-молек. құрылысы, атомдық (атомдар, иондар, молекулалар) және субатомдық (электрондар, атомдық ядролар) бөлшектерінің қозғалыс заңдары арқылы түсіндіруге болады. Қ. д-лердің (металдардың, минералдардың, т. б. ) макроскопиялық қасиеттері туралы деректерді жинақтау мен жүйелеу 17 ғ-да басталды. Қ. д-лерге әсер ететін мех. күштерді, жарықты, электр және магнит өрістерін, т. б. сипаттайтын бірнеше эмпирикалық заңдар (Гук заңы (1660), Дюлонг және Пти заңы (1819), Ом заңы (1826), Видеман-Франц заңы (1853), т. б. ) ашылды.

Қатты денедегі атомдар . Атом аралық байланыстар . Атомдар, молекулалар немесе иондар Қ. д-нің құрылымдық бірліктері қызметін атқарады. Қ. д-нің кристалдық құрылымы атомдық бөлшектер арасындағы әсер етуші күштерге тәуелді. Сыртқы қысым көмегімен атомдар аралығындағы ара қашықтықты өзгерте отырып, Қ. д-нің кристалдық құрылымы мен қасиеттерін айтарлықтай өзгертуге болады. Сонымен қатар Қ. д-нің құрылымы мен қасиеттері темп-раның өзгерісіне, магнит өрісінің әсеріне, басқа да сыртқы әсерлерге байланысты өзгереді. Байланыстарының түрі бойынша Қ. д. 5 класқа бөлі-

неді (иондық, атомдық, металдық, молекулалық, сутектік) . Иондық кристалдарда (NaCl, KСl, т. б. ) электрондар бір атомнан екінші атомға өтіп, иондар түзеді. Иондар арасындағы негізгі өзара әрекеттесу күші - электрстатик. тартылыс күштері болып табылады. Ковалентті байланыстағы кристалдарда (алмаз, Ge, Sі) көршілес атомдардың валенттік электрондары ортақтастырылып, нәтижесінде электрондық тығыздығы жоғарылайды және оның белгілі бір бағыты болады. Мыс., алмаздың құрылымы осы байланысқа жатады. Мұндағы кристалл аса ірі молекуланы елестетеді. Металдық кристалдарда (Cu, Al, Na) еркін өткізгіштік электрондар байланыс энергиясын тудырады: металды электрондық сұйыққа батырылған оң иондардан тұратын тор деп қарастыруға болады. Барлық металл кристалдары негізінен металдық байланыстың нәтижесінде пайда болады. Осымен қатар кейбір металдар үшін (вольфрам, темір, қалайы, марганец, т. б. ) коваленттік байланыста маңызды болып табылады. Молекулалық кристалдарда молекулалардың динамик. поляризациялануы салдарынан молекулалар әлсіз электрстатик. күштермен (Ван-дер-Ваальс күштерімен) байланысады (қ. Молекула аралық өзара әсер) . Сутектік байланысты кристалдарда [H2O (мұз), HF] сутегінің әрбір атомы тартылыс күші әсерінен бір мезгілде басқа екі атоммен байланысады. Бұл байланыс су молекулаларының арасындағы өзара әрекеттесудің маңызды түрі. Ол су молекулаларының дипольдық моменттерінің электрстатик. тартылысымен бірге су мен мұздың қасиеттерін қалыптастырады. Қ. д-ні байланыстар бойынша классификациялау шартты нәрсе, себебі көптеген заттарда байланыстың бірнеше түрлі комбинациялары байқалады (қ. Кристаллохимия) . Қ. д-дегі атомдық бөлшектердің арасындағы әсер етуші күштер әр түрлі болғанымен, олардың негізгі көзі электрстатик. тартылыс және тебіліс күштері болып табылады. Өзара әсерлесу күштері туралы білім Қ. д-нің күй теңдеуін алуға мүмкіндік береді. Барлық Қ. д-лер жоғары темп-рада балқиды немесе кебеді (қатты гелийден басқасы; қатты гелий қысымның күшімен темп-ра төмендегенде балқиды) . Балқу процесінде денеге берілетін жылу атомдар арасындағы байланысты үзуге жұмсалады. Қ. д-нің балқу темп-расы (Тб) табиғатына байланысты әр түрлі болады (молекулалық сутек үшін -259, 1°С, вольфрам үшін -3410±20°С, графит үшін 4000°С-ден жоғары) .

Диамагнитизмнің классикалық теориясы

Магнит өрісінде қатты денелерлегі магниттік момент векторы u сыртқы магнит өрісінің кернеулігіне қарсы бағытталады

$\mu = x_{d}*H$

Бұл жердегі z <0-заттың димагниттік бейімделгіштігі теріс шама. Біраз металдар: мыс, күміс, алтын, $берилий$ , цинк, кадмий, сынап, қорғасын, висьмут, т. б. қатты денелер жəне инертті газдар диамагниттік болады.

Сыртқы магнит өрісінде қозғалған электронға оның жылдамдығына перпендикуляр бағытталған Лоренц күші əсер етеді. Лоренц күші жылдамдықтың шамасын өзгертпей, тек бағытын өзгертеді. Нəтижесінде электрон шеңбер бойымен қозғалып, атом кішкене магнетикке айналады. Атомдардың магниттік моменттері қосылып, зат магниттеледі.

Айналмалы қозғалыстағы электронның бұрыштық жылдамдығы Лармор теоремасы бойынша анықталады.

$\omega_{L} = - \frac{e}{2mc}H$

Электронның заряды теріс e <0 болғандықтан w $\uparrow$ Сондықтан электронның шеңбер бойындағы жылдамдығы v мен H векторы оң бұранда жүйе құрайды. Ал дөңгелек тоқтың бағыты электронның жылдамдығына қарсы болғандықтан, j жəне H векторлары сол бұрындалы жүйе болады. Олай болса магнит өрісі əсерінен индукцияланған дөңгелек тоқтың магниттік моменті $\mu$ сыртқы магнит өрісіне қарсы бағытталады.

Ортаның магниттелуін анықтау үшін электронның механикалық моменті мен магниттік моменті арасындағы байланысты пайдаланамыз

$\mu = \frac{e}{2mc}L = \frac{e}{2mc}\lbrack r. mv\rbrack = \frac{e}{2c}\lbrack r. v\rbrack = \frac{r}{2c}\left\lbrack r. \lbrack\omega. r\rbrack \right\rbrack = \frac{{er}^{2}}{2c}\omega$

Бұрыштық жылдамдықты (8. 2) бойынша алмастырамыз.

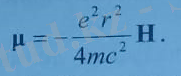
Координат жүйесінің z өсін H векторымен бағытттайық. Сонда (8. 4) тегі $r^{2} = x^{2} + y^{3}$ болады.

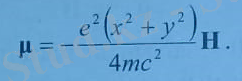
Z электрон бар атомның магниттік моменті былай анықталады:

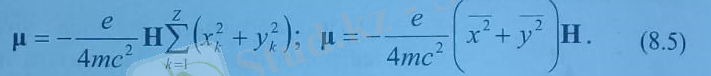
Бұл жердегі $\overline{x^{2}} + \overline{y^{2}} -$ электронның атомның центрінен орташа квадраттық ауытқуы. Егер атомдағы электрондар сфералық симметриялы орналасқан болса, $\overline{x^{2}} = \overline{y^{2}} = \overline{z^{2}} = \frac{1}{3}a^{2}$ бұндағы а элктронның атом центрінен орташа квадраттық ауытқуы. Сонда (8. 5) бойынша атомның магниттік моменті

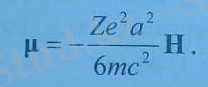
Заттың бір көлем бірлігінің магниттік моментін -магниттелу векторы деп атайды жəне М арқылы белгіленеді. Бір көлем бірлігіндегі атомдар саны N болса, (8. 6) бойынша

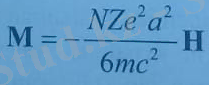
Бұдан заттың диамагниттік бейімделгіштігін анықтайтын Лан -жевен формуласын жазамыз.

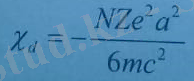
Заттың мольдік диамагниттік бейімделгіштігін енгізуге болады. Ол үшін соңғы формулаға N Авогадро санын қойып, e, m жəне с тұрақтылардың сан мəндерін қойып, мына түоде жазуға болады.

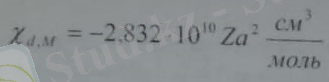
Диамагнетизмнің кванттық теориясы

Кванттық механикада атомдағы электронның импульс моменті L векторының z өсіндегі проекциясы $L_{z} = mh$ (бұл жердегі m- магниттік кванттық сан) болатын стационар жағдайда магниттік моменті де болатыны көрсетіледі. Атомның магниттік моменті оның механикалық моментіне пропорционал болады.

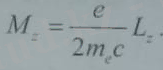
Пропорционалдық коэффициент табиғаттың іргелі тұрақтылары арқылы өрнектелген.

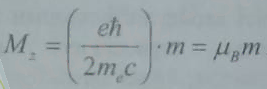
Бұл жердегі пропорционалдық коэффициент- Бор магнетоны деп аталады.

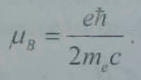
Бор магнетоны кванттық механикадағы ең аз элементар магниттік момент болып табылады.

Кванттық механика бойынша магнит өрісіндегі тоқ тығыздығы

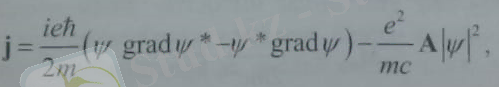
Бұндағы А- магнит өрісінің вектор -потенциалы. Радиусы r дөңгелек токтың элементі dI= $j_{\varphi}\sigma dl = j_{\varphi}dV, \sigma -$ тоқ трубкасының көлденең қимасының ауданы, dl=rd $\varphi$ -тоқ сызығы бойындағы кішкене доғаның ұзындығы. Цилиндрлік координат жүйесіндегі dl тоқ элементінің магниттік моменті

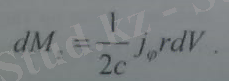
Тоқ тығыздығы үшін (8. 12) формуласын қоямыз жəне тоқтың көлемі бойынша интегралдап, толық магниттік моментті анықтаймыз.

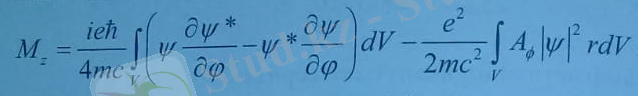
Бірінші интеграл, магнит өрісі жоқ кездегі сутегі типтес атомның магниттік моменті, (8. 10) бойынша жазылған магниттік моментке тең.

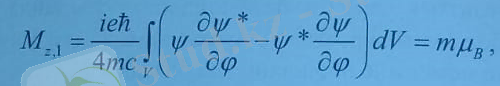
(8. 14) -тегі екінші интеграл магниттік моментті сыртқы магнит өрісіне байланысты бөлігі.

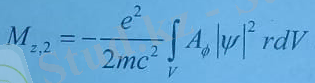
Біртекті магнит өрісі кернеулік векторын z өсімен бағыттасақ, цилиндрлік координат жүйесіндегі вектор -потенциалдың құраушылары :

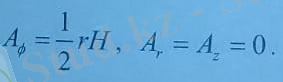
Сонда (8. 16) формуласы былай жазылады:

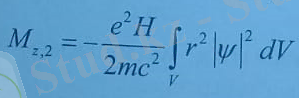
Бұл жердегі интеграл $r^{2}$ - тың орта мəні. Сонда

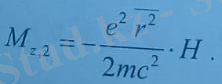
Бұл формула сутегі атомы үшін (8. 4) формуласымен бірдей жəне атомдардың диамагниттік қасиетін көрсетеді.

Заттардың магниттік қасиеттері. Парамагнетизм

Затты сыртқы магнит өрісіне орналастырған кезде оның dV көлемінің магниттік моменті магнит өрісі кернеулігіне байланысты 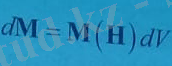болады. Заттың бір көлем бірлігінің магниттік моменті М- магниттелу векторы деп аталады жəне оның шамасы мен бағыты сыртқы магнит өрісінің Н векторына тəуелді болады. Изотропты ортада М векторы Н векторына параллель болады. М (Н ) функциясын Н -тың дəрежелері бойынша бірінші ретті аз шамаға дейін қатарға жіктесек,

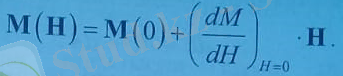
Бірінші қосылғыш нөлге тең, ал екінші қосылғыштағы

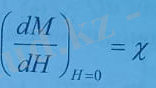
Заттың магниттік бейімделгіштігі деп аталады. Сонда

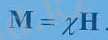
X-дің шамасы мен таңбасына қарай, магнетик заттарды үш топқа бөлуге болады:

1. Х>0 болғанда М векторы Н-пен бағыттас. Ондай заттарды парамагнетиктер деп атайды. Мысалы, оттегі газы, сілтілі металдар парамагнетиктер болады.

2. Х <0 болғанда М векторы Н векторына қарама-қарсы бағытталады жəне ондай заттарды диамагнетиктер деп атайтынын жоғарыда келтірдік. Инертті газдар диамагнетиктер болады.

3. Феррлмагнетик заттардың магниттелу векторының сыртқы магнит өрісіне тəуелділігі өте күрделі. Кейбір заттарда сыртқы магнит өрісін өшіріп қойғанда да нөлден өзгеше магниттелу векторы сақталып қалады.

Магнетиктер үшін кейбір термодинамикалық қатынастарды келтірейік. Магниттік моменті М' болатын денеден R қашықтықта орналасқан екінші дене берілсін. Денелердің өлшемдері олардың ара қашықтығына қарағанда əлдеқайда аз болсын. Бірінші дене, екінші дене орналасқан нүктеде Н магнит өрісін туғызады.

Бұл өрісі екінші денені магниттейді, яғни ол М магниттік моментке ие болады. Екі магнетиктің арасында 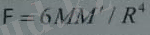тарту күші пайда болады. Егер денелердің арасын dR-не арттырсақ, соңғы формулалар бойынша жүйеге қарсы 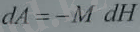жұмыс істеледі. Магнетиктің бір көлем бірлігінің ішкі энергиясының өзгерісі термодинамиканың бірінші заңы бойынша

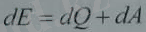
Бұндағы dQ- жүйеге қайтымды жолмен берілген жылу. Қайтымды процесс үшін $dQ = TdS$ (dS-процесс кезіндегі энтропия өзгерісі) , сонда термодинамиканың негізгі теңдеуі былай жазылады

Жүйенің бос энергиясы F=E-TS өрнегін дифференциалдаймыз

Бұдан 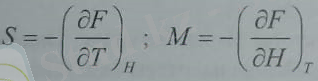(8. 20) бойынша, соңғы формуладан Н бойынша туынды алып, заттың магниттік бейімделгіштігін бос энергия арқылы анықтаймыз:

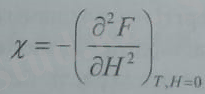
Тұрақты магниттік моменттері бар бос бөлшектер ( атомдар жүйесі берілген. Сыртқы магнит өрісіне орналасқан ондай бөлшектердің $\mu_{a}$ магниттік моменттері бір бағытқа бұрылып, реттеліп орналасады, ал олардың жылулық қозғалысы реттілікті бұзуға тырысады. $\mu_{a}$ магниттік моменті бар атомның Н магнит өрісіндегі потенциялдық энергиясы $- \left( \mu_{a}H \right) = - \mu_{a}H\cos\theta$ бұл жердегі $\theta - \mu_{a}$ жəне Н векторлары арасындағы бұрыш. Екі вектордың арасындағы бұрыштың $(\theta, \theta + d\theta)$ аралығында жату ықтималдылығы

Бұл жердегі $2\pi\sin\theta d\theta = d\Omega$ - берілген $d\theta$ бұрышына сәйкес денелік бұрыш, А- нормалау шартынан анықталатын тұрақты. $x = \cos\theta$ және $\ \alpha = \mu_{a}H \slash \kappa T$ белгілеулерр енгізіп, барлық бұрыш бойынша интеграл аламыз.

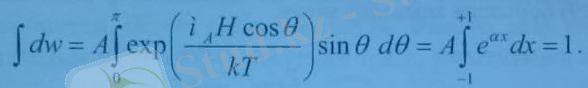
Бұдан нормалау тұрақтысын тауып, (8, 25) -ке қойып ықтималдылықтың үлестіру заңын аламыз. Сонда атомның орташа магниттік моменті былай анықталады:

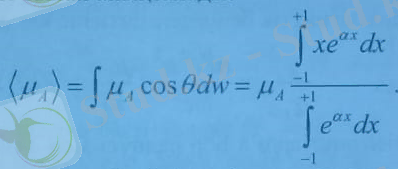
Алымындағы интеграл бөліміндегі интегралдың $\alpha$ бойынша туындысына тең, ал бөліміндегі интеграл оңай есептеледі. Сонда

Бұл жердегі L(a) - Ланжевен функциясы былай анықталады:

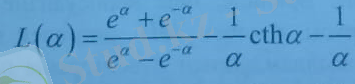
Сыртқы магнит өрісі әлсіз $\mu_{A}H \ll \kappa T$ . Яғни $a \ll 1$ болған жағдайда (8, 27) функциясын қатарға жіктеп, $L(a) \approx a \slash 3$ деуге болады. Бұл кезде магниттелу векторы

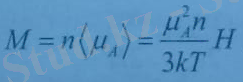
Бұдан магниттік бейімделгіштік коэффициентін былай жазамыз:

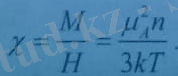
Парамагнетиктердің магниттік бейімделгіштік коэффициенті температураға кері пропоционалдығын білдіретін-Кюри заңын аламыз.

Қорытынды

Магнетизм - 1) электр токтарының, токтар мен магниттік моменті бар денелердің (магниттердің) және магниттердің араларындағы өзара әсерлесудің ерекше түрі; 2) физиканың осы өзара әсерлесуді және осындай қасиеттер білінетін заттарды (магнетиктерді) зерттейтін бөлімі. Жалпы түрде магнетизмді қозғалыстағы электрлік зарядталған бөлшектердің арасындағы материалдық өзара әсерлесудің ерекше формасы түрінде анықтауға болады. Кеңістікпен бөлінген денелердің арасында магниттік өзара әсерлесуді қамтамасыз ететін, оны бір денеден екіншісіне жеткізетін - магнит өрісі. Ол электр өрісімен қатар, материя қозғалысының электрмагниттік формасы білінуінің бірі болып табылады. Электр өрісінің көздері электр зарядтары болып табылса, ал магнит өрісі үшін ондай көздер табиғатта әзірше анықталмаған. Магнит өрісінің көзі - қозғалыстағы электрлік заряд, яғни электр тогы. Сыртқы магнит өрісінің заттарға тигізетін негізгі екі түрлі эффектісі (әсері) белгілі: 1) Фарадейдің электрмагниттік индукция заңы бойынша, сыртқы магнит өрісі затта әрқашанда индукциялық ток тудырады және бұл токтың магнит өрісінің бағыты бастапқы магнит өрісіне қарсы бағытталады (Ленц ережесі) . Сондықтан, заттың сыртқы өріс тудырған магниттік моменті сыртқы өріске қарама-қарсы бағытталады; 2) егер атомның магниттік моменті 0-ден өзгеше болса (спиндік, орбиталдық немесе спин-орбиталдық), онда сыртқы өріс оны өз бағыты бойынша бағдарлауға ұмтылады. Нәтижесінде, магнит өрісіне параллель магниттік момент пайда болады, ол парамагниттік деп аталады. Атомдық магниттік моменттері бір-біріне параллель бағдарланған заттар ферромагнетиктер (ферромагниттер), ал осыған сәйкес іргелес атомдық моменттері антипараллель орналасқан заттар - антиферромагнетиктер (антиферромагниттер) деп аталады. Заттардың магниттік қасиеттерін қарастырғанда “магнетик” деп аталатын жалпылама термин пайдаланылады. Заттардың магниттік қасиеттері оларды құрайтын бөлшектердің магнетизмімен анықталады. Магнит өрісі - қозғалыстағы электр зарядтары мен магниттік моменті бар денелерге (олардың қозғалыстағы күйіне тәуелсіз) әсер ететін күштік өріс. Магнит өрісі магниттік индукция векторымен (В) сипатталады. В-ның мәні магниттік моменті бар қозғалыстағы электр зарядына және денелерге өрістің берілген нүктесінде әсер етуші күшті анықтайды. “Магнит өрісі” терминін 1845 ж. ағылшын физигі Майкл Фарадей енгізген. Макроскопиялық магнит өрісінің көздері - магниттелген денелер, тогы бар өткізгіштер және қозғалыстағы зарядталған денелер. Айнымалы магнит өрісі - электр өрісінің, ал электр өрісі магнит өрісінің уақыт бойынша өзгерісі нәтижесінде пайда болады. Электр және магнит өрістері, олардың бір-бірімен өзара әсерлері Максвелл теңдеуімен толық сипатталады. Магнит өрісінің кернеулігі (Н) мен магнит индукциясы (В) - өрістің күштік сипаттамасы. Кернеулік векторы өріс пайда болған орта қасиетіне тәуелсіз шама болса, индукция векторы қарастырылатын денедегі қорытқы өрісті сипаттайды. Сондай-ақ, индукция векторы магнит өрісінде қозғалған зарядқа әсер ететін күшті, магниттік моменті бар денеге магнит өрісінің тигізетін әсерін, өріс тарапынан байқалатын басқа да әсерлерді анықтайды. Табиғатта магнит өрісінің сан алуан түрі кездеседі. Техникада магниттік дефектоскопия мен бақылаудың магниттік әдістері кең қолданылыс тапты. Магниттік материалдар генератор, трансформатор, реле, сондай-ақ магниттік күшейткіштердің, магниттік жады (есте сақтау) элементтерінің магниттік сымдарын (өткізгіштерін), компас тілдерін, т. б. магниттік жазу таспаларын жасауда қолданылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.