y = kx + l сызықтық функциясының анықтамасы, графигі және ерекше жағдайлары

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 2 бет
Таңдаулыға:

Сызықтық функция

y = kx + l (мұндағы x - тәуелсіз айнымалы, k мен l - нақты сандар) түріндегі формуламен берілетін фуннкцияны сызықтық функция деп атайды.

у = kx + l функциясының анықталу аймағы барлық нақты сандар жиыны.

Егер у = kx + l сызықтық функциясындағы l = 0 болса, онда у = kx түрінде жазылады. у = kx функциясы тура пропорционалдық деп аталады.

Егер у = kx + l формуласындағы k = 0 болса , у = 0x+l , онда у = l; у = l функциясы тұрақты функция деп аталады. у = l тұрақты функциясы сызықтық функцияның дербес жағдайы.

Сызықтық функцияның графигі

У = 1, 5x - 2 сызықтық функциясының графигін сызайық.

Ол үшін x пен y-тің сәйкес мәндерінің кестесін құрастыру керек.

-3

-2

-1

х: у

-3: -6, 5

-2: -5

-1: -3, 5

0: -2

1: -0, 5

2: 1

3: 2, 5

Координаталық жазықтықта координаталары кестеде көрсетілген нүктелерді белгілейік.

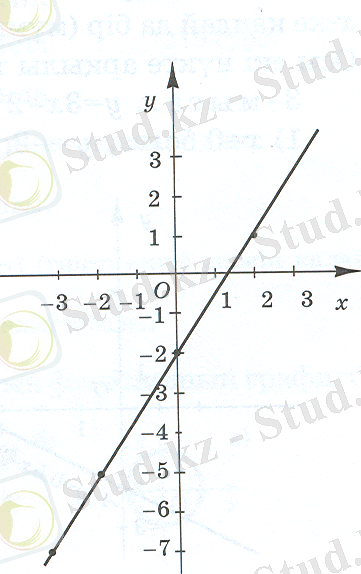Белгіленген нүктелерді қоссақ, түзу сызылады. Осы түзу у = 1, 5x - 2 сызықтық функциясының графигі болады. y = kx + l функциясының графигі түзу сызық.

Жазықтықтағы екі нүкте арқылы бір ғана түзу жүргізілетіндіктен, түзуді жүргізу үшін, оның екі нүктесінің координаталарын білу жеткілікті.

Y = kx + l сызықтық функциясының графигі болатын тузу ординаталар (Оу) осін (0; l) нүктесінде, ал абциссалар (Ох) осін ( 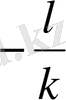; 0) нүктесінде қияды.

Сызықтық функцияның дербес жағдайлардағы графигі

l=0 және k 0 болғанда у=kx тура пропорционалдығының графигін қарастырайық.

у=kx функциясының формуласынндағы х =0 болғанда у =0. Сондықтан оның графигі координаталар басы арқылы өтеді.

у=kx (мұндағы k 0) функциясының графигі координаталар басы арқылы өтетін түзу.

у=kx тура пропорционалдығының графигін салу үшін ізделінді нүктелердің бірі ретінде О(0; 0) нүктесін алу керек.

Ізделінді екінші нүктенің координаталарын табу үшін x-тің нөлден өзгеше қандай да бір (мүмкін) мәнін қойып, оған сәйкес у- тін мәнін табу керек.

Мысалы, у=2х функциясы үшін, х=2 болғанда у=4. А(2; 4) нүктесін алу керек. Табылған О(0; 0) және А(2; 4) нүктелері арқылы жүргізілген түзу у=2х функциясының графигі.

у=kx функциясы графигінің координаталық жазықтықтағы орналасуы к коэфицентіне тәуелді. у=kx функциясында, егер х=1 болса у=k.

у=kx функциясының графигі -О(0; 0) және (1; к) нүктелері арқылы өтетін түзу.

Егер к 0 болса, у=kx функциясының графигі I және IIIкоординаталық ширектерде, ал k 0 болса, II және IV координаталық ширектерде орналасады.

у=kx функциясының графигі мен у=kx+l функциясының графигі k- ның бірдей мәнінде өзара параллель түзулер. х-тің кез келген мәні үшін у = kx+ l функциясының мәні у=kx функциясының мәнінен l-ге артық.

у = kx+l функциясындағы к=0 болса, функция у=l формуласы-мен жазылады. у=l формуласының графигі абциссалар осіне параллель, абциссасы 0; ординаталары l болатын түзу.

Алдамұратова Т. А. Математика. 6-сыныпқа арналған оқулық. -Алматы Атамұра, 2002.

Н. Нұрмақов атындағы

№ 2 мектеп-интернаты

Орындаған:

Тексерген: Уатаев Н. С.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.