Уақыттық қатарларды талдау

Реферат

Математика пәнінен

Тақырыбы: Уақыттық қатарларды талдау

Уақыт қатары - идеалды жағдайда «нақты анықталған сан (көлем) ретті, тең уақыт аралығындағы нүктелерде бір кезең барысында жазылып отыратын» мәліметтер жиынтығы, атап айтқанда, бөлшектік баға индексі. Мәліметтер осы қатаң критерийлерді қанағаттандырмайтын (мысалы, қатынастардағы дұрыс емес стандартталған айнымалылар немесе аралықтар) және жазылатын интервалдар бірдей емес болатын жерде, егер мәліметтер уақыт аралықтарына сәйкес келсе, уақыт қатары туралы айтуға болады. Уақыт қатары мәліметтерінің негізгі көзі халық санағы болып табылады.

Уақыттық қатарлар - уақыттың бірнеше жалғасқан кезеңдері бойынша бір объект, процесс жөніндегі деректер, яғни зерттеліп отырған объект, процесстің даму динамикасы сипатталады. Мысалы: инфляция немесе орташа жалақы не ұлттық табыс бойынша тоқсан сайынғы( ай сайынғы, жылдық, т. б. ) деректер; валютаның күнделікті бағамы; биржада мемлекеттік қысқа мерзімді облигацияларға баға белгілеу және т. с. с.

Тәжірибеде нәтижелік факторға көп себепші факторлар әсер етеді, олардың кейбіреуі сандық өлшенбесе, ал кейбіреулерін бақылау мүмкін емес. Сондықтан, барлық факторлардың әсер етуі туралы ақпараттың қайнар көзі болып, ізделініп отырған нәтижелі фактордың уақыт периодындағы мәндерінің динамикасы. Уақытқа сәйкес әр түрлі құбылыстардың өзгеруі - динамикалық қатардың негізгі мәселесі болып табылады. Динамикалық қатар уақыт периодындағы айқын статистикалық көрсеткіштегі, яғни хронологиялық ретте орналасқан сандық мәндерді білдіреді. Экономикалық көрсеткіштің динамикалық қатарын құратын сандық мәліметтерді қатар деңгейі деп атайды және оны У(у ₁ , у ₂ , … у _п ) түрінде көрсетеді. Қатардың бірінші мүшесін у ₁ бастапқы деңгейі, ал соңғы мүшені у _п ақырғы деп атайды. Уақыт периоды t арқылы бейнеленіп, есептеу 1-ден бастап, яғни 1, 2, 3 . . . деп жалғасады. Динамикалық қатар кесте немесе графикалық түрде бейнелеуге болады. Графикалық түрде болғанда, абцисса осінде уақыт шкаласы t, ал ординатада - У қатары.

Динамикалық қатар абсолютті, салыстырмалы және орташа шамалармен өрнектелуі мүмкін. Салыстырмалы мөлшердегі қатар қандайда бір көрсеткіштің өзгеру қарқынын көрсетеді. Мысалы, жыл сайынғы фермерлік шаруашылықтардың саны абсолюттік өлшеммен алынған. Соңғы онжылдықта ай сайын орташа өндірілген мұнай көлемі. Мұнда берілген периодқа сәйкес орташа мәндері есептеліп алынған. Практикада қатарлар интервалды және моментті болып бөлінеді. Динамикалық қатар деңгейі қандай да бір уақыт моментіне немесе периодқа байланысты болуы мүмкін. Моментті қатар - қандай да бір нақты уақытқа сәйкес көрсеткішті бейнелейтін деңгей. Интервалды қатар деп - белгіленген периодқа есептелген көрсеткішті бейнелейтін деңгейді айтамыз. Бұл деңгейлерді ұсақтап және ірілендіруге болады. Мұнайды айына қанша мөлшерде алатындығын білсек, біз оның жылдық немесе кварталдық көлемін біле аламыз. Мысалы, жолды жөндеу күніне километрлеп беріледі. Осы арқылы айына немесе он күнде жөнделген жолдың көлемін біле аламыз.

Деңгейлердің салыстырмалылығы және динамикалық қатарлардың сәйкестігі. Динамикалық қатарларға қойылатын талаптардың бірі- салыстырмалылық:

- есеп пен есепке алу әдісінің сәйкестігі. Мысалы, өнімділіктің жиналған ауданнан немесе себілгеннен егістікке сәйкес есептелуі, өнеркәсіпте бір жұмысшының немесе бір қызметкердің еңбек өнімділігі қарастырылады.

- есептеу уақытының өзгеруі. Мал саны 1 қаңтарға немесе қазанға есепке алынған.

- бірліктердің сәйкестігі: өн бойы метрлер және шаршы метрлер, бағалар.

- периодтардың әр түрлі ұзақтылығы.

Динамикалық қатар деңгейлерінің өзгеру көрсеткіштері. Уақытқа сай даму жылдамдығын статистикалық көрсеткіштер көмегімен деңгейлерді өзара салыстыру арқылы сипаттаймыз. Оларға: абсолютті өсу, өсу қарқыны және өсімше қарқыны.

Абсолютті өсімше ( У) екі қатар деңгейінің арасындағы айырмашылық есептелінеді және тізбектік немесе базистік болады.

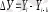
егер к=1 болса, онда Yі - деңгейі берілген қатар үшін кейінгі, ал Y _i-1 алдынғы қатар деңгейі болады да, абсолютті өсімше қатар деңгейінің тізбектік өзгеруін көрсетеді.

Өсу қарқыны - салыстырмалы көрсеткіш, екі қатар деңгейінің қатынасы. Өсу коэффициенті берілген қатар деңгейінің базистік деңгейден қанша есе үлкен немесе кіші екендігін көрсетеді. Базистік деңгей ретінде зерттеу мақсатына байланысты бәріне тұрақты қандай да бір деңгейдің барлық деңгейге қатынасын айтамыз.

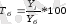және

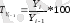
Өсу қарқыны - берілген деңгейдің салыстыру базасы ретінде қабылданып отырған деңгейден қанша есе көбірек екендігін көрсететін салыстырмалы көрсеткіш. Екі түрлі есептеуге болады.

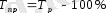немесе

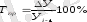
Төмендегі 15 кестеде 2003-2008жылғы мәліметтер бойынша жоғарыдағы формулалар бойынша динамикалық қатардың деңгейлерінің өзгеруіне сипаттама беру үшін олардың көрсеткіштерін есептейміз.

Уақыт қатарының автокорреляциялық деңгейі

Уақыт қатарының деңгейінің арасындағы корреляциялық тәуелділігін қатардың автокорреляциялық деңгейі деп аталады.

Оны сандық жағынан сызықты корреляция коэффициенті арқылы табуға болады.

Корреляция коэфицентінің есептелу формуласы :

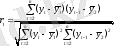
мұндағы

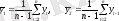
осы шаманы 1 ші ретті қатар деңгейінің автокорреляция коэффициенті деп атайды. Бұл шама көршілес t және . екі қатар деңгейінің тәуелділігін өлшейді

Осылайша, автокорреляция коэффициентінің 2 не одан да үлкен ретін табуға болады. 2 ші ретті авторкорреляция коэффициенті және деңгейлері арасындағы тығыздықты анықтайды және мына формуламен анықтадалы:

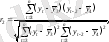
мұндағы

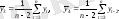
автокорреляция коэффициенті есептелетін жиілік саны лаг деп аталады. Жұп мәндердің санының лагы өссе, онда коэффициент кемиді Максималді лаг . Автокорреляцияның екі негізгі қасиеттерін атап өтейік: біріншіден, ол сызықтық корреляция коэффициентінің негізінде құрылады және тек сызықтық байланыстың осы және өткен қатар деңгейлерінің тығыздығын сипаттайды. Екіншіден, автокорреляцияның коэффициентінің таңбасы бойынша қатар деңгейлеріне өсу және кему тенденциясы туралы қорытынды жасауға болмайды.

Бірінші, екінші т. б. авторкорреляция коэффициентінің тізбегін уақыт қатарының автокорреляциялық функциясы деп атайды.

Функцияның мәндерінің және лагтарының арасындағы тәуелділіктің графигі коррелограмма деп аталады.

1. Динамика қатарындағы негізгі тенденцияны зерттеу әдісі

Кез келген қатардың деңгейі - бұл әр түрлі факторлардың өзара байланысы, олар зерттеліп отырған көрсеткішке ұзақ уақыт бойынша және әр түрлі бағытта әсер ете алады. Бұл факторлардың зерттеу кезінде әр түрлі үйлесімділікте қатар деңгейінің тәуелділігі әр түрлі формаларды қабылдай алады. Бір жағдайда факторлар оның көбею немесе кему тенденциясын қалыптастырады, ал басқа жағдайда циклдік ауытқуларға шалдығады.

Кесте 15. Динамикалық қатар көрсеткіштері

Динамикалық қатарларда орта көрсеткіштерді есептеу .

Динамикалық қатар сипаттамасы ретінде қатардың орташа деңгейі У _орт алуға болады. Ол орташа хронологиялық деп аталады. Интервалдық қатарда тұрақты периодты абсолюттік шамалардың орташа деңгейі арифметикалық орта шама болады. Мысалы,

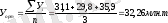
Әр түрлі динамикалық қатарлар үшін орта мәні әр түрлі әдіспен есептеледі. Моменттік қатар үшін аз ғана өзгешелік бар. Бірдей моменттік аралыққа бөлінген п деңгейлі қатар үшін мына формула қолданылады:

Бұл орта шама статистикада моменттік қатарлар үшін хронологиялық орта мән болып есептелінеді.

Егер момент араларындағы уақыт бірлігі әр түрлі болғанда, оны әр момент үшін орташа арифметикалық формуламен есептеуге болады.

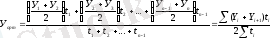
Мысалы, 2015 ж. қоймадағы тауар қалдықтарының мәліметтері келесі кестеде көрсетілген

Кесте 16. Қоймадағы тауарлық қалдықтар туралы мәліметтер

Онда 2005ж. орташа 1 айдағы тауарлық қалдық мынаған тең болды:

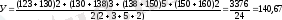
Қатардың орташа абсолюттік өсімшесі жеке тізбектелген өсімше тәріздес арифметикалық орта мән формуласымен есептеледі.

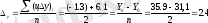
Динамикалық қатарларда орташа өсу қарқынын есептеуге ерекше мән беріледі. Көп жағдайда орташа өсу қарқыны алдыңғысына қатысты әр периодта тізбектелген өсу қарқынынан тұратын орташа геометриялық түрінде есептелінеді.

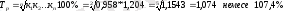
немесе

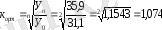
Сонымен қатар, өсу деңгейінің орта коэффициентін есептегенде шеткі деңгейлерге ғана мән бермей, кейде деңгейдің барлық сомасына да мән берген дұрыс. Мысалы, инвестиция енгізу, тұрғын үй аудандарын іске қосу, автомобильдік жолдар құрылысын жасау сияқты мәселеге келгенде, бұл жерде тек шеткі деңгейді ғана емес, анализ жасалған периодтың сомасы шығатын орташа өсу қарқынын анықтаған жөн. Бұдан орта мән параболалық деп аталады және төмендегідей формуламен есептелінеді:

Мысалы, берілген 17 кесте бойынша берілген 2010-2016ж. іске қосылған тұрғын үй аудандарының орташа өсу коэффициентін анықтау керек.

Кесте 17 - Тұрғын үй аудандары көлемі

Алдымен орташа өсу қарқынын анықтаймыз

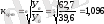
яғни жыл сайын тұрғын үйлерді іске қосу 9, 6% өседі. Жылдық өсу қарқынын есептеу үшін іске қосылған тұрғын үйлердің бүкіл периодтағы сомалар қосындысын есептеп алып формулаға қоямыз.

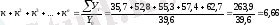
п=5 болғанда 6, 66-ге жақын мәнді аламыз және ол к=1, 095 немесе Т=109, 5% шамаларына сәйкес келеді. Бұл тұрғын үйдің жылдық іске қосылуы орташа мәнмен 9, 5% өсіп отырады дегенді білдіреді.

Уақыт қатарын тегістеу. Даму тенденциясының моделі. Аддитивті моделі.

Көп жағдайда динамикалық мәліметтер тенденция, кезеңдік және кездейсоқ компоненттерден, ал көбінесе барлық 3 компоненттен тұрады. Олардың әр деңгейі кезеңдік ауытқулар және кездейсоқ компоненттер әсерімен қалыптастырылады. Сондықтан көрсеткіштің дұрыс заңдылықпен өзгеруі үшін өзгерістің негізгі және кездейсоқ қысқа уақытта туындаған ауытқулар тенденциясын айыра білу керек. Ол үшін динамика қатарлары қайта өнделеді.

Динамика қатарларын өңдеудің бірнеше әдісі бар, олар: интервалды ірілендіру әдісі, жылжымалы орта әдісі. Өңделген қатар сосын аналитикалық әдіспен математикалық өрнегі табылады. Барлық әдістерде қатарды қайта өңдеу кезінде нақты деңгейдің орнына сол немесе басқа әдіс арқылы кездейсоқ факторлардың әрекеті әлсізденеді және сонымен бірге деңгейдің тербелісі төмендейтін басқа теңдеулер есептеледі. Нәтижесінде бастапқы нақты мәліметтерге қатысты «тегістелген», «өңделген» қатар болады. Қайта өңдеу динамика қатарларын өңдеу немесе тегістеу әдістері деп аталады.

Интервалдарды ірілендіру әдісі. Қатардың деңгейлерін өңдеудің ең қарапайым түрі - зерттеліп отырған көрсеткіштің уақыт интервалдарын ірілендіру. Бұл әдісте уақыт периоды қысқа мерзімдерді көрсеткенде ғана ыңғайлы болады. Мысалы, егер әр күндік немесе әр айлық сауда немесе тауардың өндірілуі туралы мәліметтер болса, қатардағы деңгейлердің тербеліс периоды аз шама болғанына байланысты оларға әсер ететін кездейсоқ факторлардың да көп болуы мүмкін. Мұндай әсердің болуына жол бермес үшін уақыттың аралығын ірілендіру ұсынылады, мысалы, күнделікті мәліметті 5-ке немесе 10 күнге дейін, әр айды тоқсанға және т. с. с.

Мысал 1 . Өнеркәсіптің 2 жылдық әр айдағы өнім өндірілуі туралы мәліметтер бар (кесте 18) . Кестеде екінші графада жиырма төрт айдың динамикалық мәліметтері берілген. Берілген мәліметтердің графигін салсақ (сурет 7), ауытқулардың көп екендігін көреміз. Оның тренд теңдеуінің детерминация коэффициенті R ² =0, 68, өте үлкен емес.

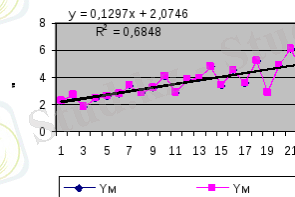
Сурет 7. Айлық мәліметтердің графигі

Жылжымалы орта әдісі. Бұл әдіс уақыт периоды ірілендіруге келмеген жағдайда, немесе мәліметтер саны жеткіліксіз болғанда пайдаланған ыңғайлы. Мұнда нақты деңгейлер қатардың m деңгейлерін топтастырып жылжымалы түрде ірілендірілген интервалдар үшін есептелген орта деңгейлермен алмастырылады. Мысалы, m=3 деп қабылдасақ, онда алғашқы 3 деңгейлердің орта шамасы есептеледі, одан соң бір деңгей жылжып келесі үшеуінің орта шамасы табылады, сөйтіп, жылжый отырып, әр кезді 3 деңгейдің сомасында жаңадан бір деңгей пайда болады (кесте 17, сурет 10) .

Берілген мәліметтерді үштен және төрттен топтастырып бір мәнге жылжу арқылы есептелген мәндердің графигі тегістелгенін байқауға болады. Қаншадан топтастыруды алдын ала анықтау қиын, есептеп графигін салыстыру арқылы шешім қабылдауға болады.

Енді үштен топтастырған мәліметтердің тренді теңдеуі Y=6, 4792+0, 3994t адекватты, R ² =0, 93 (сурет 11 )

Сурет 11- Үштен топтасқан мәліметтердің тренді теңдеуі

Төрттен топтастырып тренді теңдеуін анықтасақ үштен топтастырғанға қарағанда теңдеудңғ адекваттылығы жоғары екенін көреміз (сурет 12 ) .

Сурет 12 - Төрттен топтасқан мәліметтердің тренді теңдеуі

Аналитикалық әдіс. Динамика қатарын қайта өңдеу әдісі қатар деңгейінің мәліметтерін аналитикалық формула бойынша өрнектеу болып табылады. Аналитикалық әдіс мәліметтерді уақыт функциясы ретінде қарастыратын Y _i =f(t) трендінің математикалық моделі. Таңдалған тренд теңдеуі бойынша есептелген Y _i -дің нақты теңдеуін Y _i * теориялықпен алмастырылуында.

Соның өзінде әр нақты деңгей y _i екі қосынды ретінде қарастырылады: 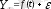, мұндағы 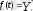- теңдеумен өрнектелген тренді, ал E _i -трендінің аймағындағы қатар деңгейінің тербелісін шақыратын кездейсоқ шама.

Аналитикалық әдіс келесі кезеңге тұрады.

1-кезең . Нақты мәліметтер негізінде зерттеліп отырған көрсеткіштің тенденциясын адекватты түрде көрсететін уақыт функциясының түрін анықтау;

2-кезең . Теңдеу параметрлерін табу.

3 кезең . Қатардың деңгейін теориялық теңдеу бойынша есептеу;

Бірінші кезең ең жауапты. Көбінесе мынадай қарапайым функциялар қолданылады.

- сызықтық функция,

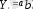- көрсеткіштік функция,

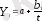- гиперболалық функция,

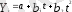- параболалық функция,

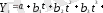- полиномды функция.

- Фурье қатары, к - гармоника саны.

Динамика қатарының деңгейлерін тегістеу үшін функцияны таңдау нақты мәліметтердің графикалық бейнесінде немесе компьютер негізінде іске асырылады. Қандай қисық жақсы нәтиже беретінін білу үшін әдетте R ² салыстырылып қаралады. 1-ге жақынырақ болған функция бастапқы мәліметтерге адекватты болып келеді.

Көп жылдар бойы динамика қатарының деңгейлерін аналитикалық тегістеуге сызықтық функция өз деңгейінде қолданылып келді. Мысалы, мәліметтердің абсолюттік өсімшесі қандайда бір тұрақты болып келгенде түзу сызық бойынша тегістеу барлық уақытта тиімді. Мысалы, екінші ретті парабола қатар деңгейінің ауытқуы үдемелі немесе баяу болуы мүмкін. Егер қатар деңгейі геометриялық прогрессияға сәйкес өзгерсе, онда мұндай тенденцияны көрсеткіштік функциямен көрсетуге болады. Егер, қатар деңгейі 0-ге жақындап, бірақ одан төмендей алмайтын жағдайда болса гиперболамен өрнектеледі.

Егер қатар деңгейі ұзақ периодтармен беріліп, әр кезеңде әр түрлі қайшылық тенденцияда болса және бір функциямен сипаттау қиын болса, онда зерттеліп отырған периодты жеке бөліктерге бөлу керек және содан соң әр бір бөлікке сәйкес қисық таңдаған дұрыс. Кей кездері дәл сол эмпирикалық қатарды әр түрлі аналитикалық формула бойынша теңестіруге болады, соның нәтижесінде едәуір адекватты нәтиже алуға болады. Қандай функцияны қолданған ең жақсы нәтиже береді деген сұраққа жауап беру үшін, әдетте, әр түрлі функция бойынша шығарылған эмпирикалық деңгейдің квадрат сомасы мен әр түрлі функциямен есептелген теоретикалық мәнімен салыстырады. Ауытқулардың квадрат сомасы қайсысында кішірек болса, сол функция таңдалады.

Мысалы, алдыңғы мысал бойынша тренд теңдеуін сызықтық функция ретінде өрнектеп, теңдеудің адекваттылығын тексеріп болжамға пайдалануды қарастырдық.

Маусымдық және циклдік тербелістер. Болжаудың аддитивті және мултипликативті әдістері.

Динамика қатары әр түрлі өзара әсер ететін факторлар әсерінен құрастырылады, біреуі даму тенденциясын анықтаса, екіншісі ауытқуды анықтайды. Бұл кезде ауытқу қандай шамаға қатысты зерттеліп отырғанын ескеру керек. Мысалы, абцисса осіне паралель өтетін У _орт қатар деңгейінің орта мәнінен ауытқуын зерттеуге болады. Сонымен қатар, деңгей ауытқуларын тренд сызығына қатысты зерттеуге болады. Деңгейлері айлық немесе тоқсанға сәйкес жинақталған динамика қатарында кездейсоқ ауытқулармен қатар жыл сайын жеке айларда немесе кварталдарда деңгейлердің жоғарылауы мен төмендеуі қайталанып отырады, немесе маусымдық ауытқулар байқалады. Маусымдық ауытқулар өлшенеді. Барлық өлшемдер әр айдың нақты деңгейлерін орта деңгейлермен салыстыруға негізделеді. Маусымдық ауытқуды өлшеу үшін нақты деңгейдің орта деңгейден абсолютті айырымы, не айлық деңгейлердің жылдық орташа айлық деңгеймен қатынасы есептелуі мүмкін.

Фурье қатары

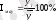
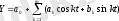к- гармоник саны

Егер қатарда деңгейдің периодты бір қалыпты өзгерісі байқалса, онда ол Фурье қатарымен зерттеуге болады. Динамикалық қатардың деңгей тербелісі синусоидалық тербеліс түрінде көрсетуге болады. К- гармоникалары реті деп аталады. Егер к=1 болса, онда Фурье қатары былай жазылады

У=а ₀ +а ₁ cost+b ₁ sint.

к=2 болғанда

У=а ₀ +а ₁ cost+b ₁ sint+ а ₂ cos2t+b ₂ sin2t

және тағы сол сияқты.

Параметрлер келесі формула бойынша есептелінеді

, ,

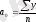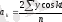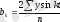
п-қатардың деңгей саны, t период өлшемі, әдетте 0-ден басталып 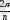тең болатын периодпен өсіп отырады. Мысалы, n=12 болғанда t уақыт периоды мына мәндерге тең

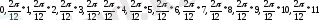
Мысалы, егер 12 айдағы қысқы киімнің сату көлемі белгілі болса, онда келесі айларға болжам жасау (20-кестеде) керек.

20-Кесте. Сату көлемі бойынша айлық мәліметтер

к=1 болғанда, 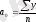=46, 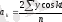=-11, 04, 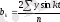=5, 74

онда Y=46-11. 04cost+5. 74sint

к=2 болғанда, 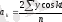= 2, 9, 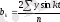= - 1, 3, онда екінші гармоника теңдеуі Y= 46-11. 04cost+5. 74sint +2, 9cos2t-1. 3sin2t

21-Кесте. Есептеу кестесі

Бастапқы теңдеулерге cost, sint, cos2t, sin2t мәндерін қоя отырып, У _т теоретикалық мәнін аламыз. Бұл теңдеудің адекваттылығын айырманың квадраттарының қосындысы арқылы тексеріледі 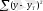, қаншалық аз болса, соншалық ол жақсы.

Мұнда к=1 болғанда, 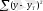=286, 88, к=2 болғанда 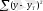=232, 22. 3. Гармоникалар 3 және 4 болғанда да осылай есептеліп, ең аз мәндеріне сәйкес теңдеуді таңдаймыз.

Уақыт қатарының модельдерімен болжам жасау. Болжамның сенімділік интервалы. Әлеуметтік- экономикалық үрдістерді болжау.

Мысалы, 2015 жылдың ай сайынғы мәліметтері бойынша ауытқудың өлшемдерін есептейік. Есептеулерді 22 кестеде көрсетеміз.

22-Кесте. Есептеу кестесі. ... жалғасы

Динамикалық қатарлар

Байланыс торабын ұйымдастыруда сигналдардың коммутациясы

Динамикалық қатарлардың ұғымы және түрлері

Банктік ісінің дамуын болжамдаудың түрлері мен модельдері

Күн белсінділігін рекурренттік талдау әдісімен зерттеу нәтижелері

Экономика дәрістер кешені

Нарық конъюнктурасын зерттеу мақсаттары

Кездейсоқ сигналдар

Сандық ақпаратты тізбектей енгізу құрылғысы

Ляпунов көрсеткіштері

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс