Дербес туындылы сызықтық дифференциалдық теңдеулерді зерттеу

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 52 бет
Таңдаулыға:

Дербес туындылы сызықтық дифференциалдық теңдеулерді зерттеу

ДИПЛОМДЫҚ ЖҰМЫСЫ

Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . ... ... ... 3
1 Дербес туындылы сызықтық дифференциалдық теңдеулер туралы 5
түсінік ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
... ... ... ... ... ... ... ... .. ... ... ... ...
1.1 Бірінші ретті дербес туындылы сызықтық дифференциалдық теңдеулер5
және оларды
шешу ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ..
...
1.2 Екінші ретті дербес туындылы сызықтық дифференциалдық теңдеулер 10
және оларды шешу ... ... ... ... ... ... ... ... ... ... ... ... ...
1.3Эллипстік типті теңдеулер ... ... ... ... ... ... ... ... ... ... ... ... ... . 14
2 Сызықтық интегралдық теңдеулер ... ... ... ... ... ... ... ... ... ... ... ... 29
2.1 Сызықтық интегралдық теңдеулерді кластарға бөлу ... ... ... ... ... 29
2.2Қысып бейнелеу әдісі және оны қолдану ... ... ... ... ... ... ... ... ... 33
2.3Фредгольм теориясы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 47
2.4Бірінші текті сызықтық интегралдық теңдеу ... ... ... ... ... ... ... .. 53
3 Практикалық 60
бөлім ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ..
... ... ... ... ... ..
Қорытынды ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... .66
... ... ... ... ... ... ... ... .. ... ... ..
Қолданылған әдебиеттер тізімі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 68

Кіріспе

Берілген жұмыста негізінен дербес туындылы дифференциалдық теңдеулер үшін
қойылған нақты есептер қарастырылады, дербес жағдайда теңдеулерді сызықтық
әдіспен баяндау үшін дербес туындылы сызықтық теңдеулердің жалпылама
шешімін табу қолданылады. Жалпы дербес теңдеулердің дифференциалдық
теңдеулер теориясының қалыптасуы ХІХ ғасырдың аяғында басталған. Бұл
теорияның негізін салушылары В.Вольтер (1896 ж.), Фредгольм (1903 ж.),
Гильберт (1912 ж.) және Э.Шмидт (1907 ж.) болып табылады. Бұл ғалымдардың
зерттеуіне дейін интегралдық теңдеулердің шешімінің құрылымы үшін біртіндеп
жуықтау әдісі ұсынылған. Бұл әдіс ең алғашында Вольтера түріндегі сызықтық
емес интегралдық теңдеулер шешімі үшін қолданылған. Теңдеуді шешудің көп
әдісі бар, бірақ олардың ішінде кейбіреулері соншалық универсалды және
Фредгольмнің бірінші, екінші текті, Вольтерраның бірінші және екінші текті
сызықтық теңдеулерінің шешімі үшін қолданылады.
Өзектілігі. Көптеген жаратылыстану, техника, механика және басқа ғылыми
білімдердің салаларының есептері формула түріндегі математикалық модельдеу
процесстеріне келтіріледі, яғни функционалды қажеттілік түрінде болады.
Мысалыға алсақ, радиотехникадағы көшу процесстері, космостық объектілердің
қозғалысы, экономикалық дамудың моделі дербес туындылы дифференциалдық
теңдеулер көмегімен зерттеледі.
Осының бәрі жұмыстың тақырыбын таңдаудың басты себебі болды.
Берілген зерттеудің объектісі дифференциалдық теңдеулер болып табылады,
ал дербес туындылы дифференциалдық теңдеулер көмегімен шешілетін
жаратылыстанудың көбінесе белгілі есептері берілген жұмыстың субъектісі
болып табылады.
Дипломдық жұмыстың мақсаты дербес туындылы сызықтық дифференциалдық
теңдеулерді зерттеу, соның ішінде біртекті сызықты, біртексіз сызықты,
сызықтық емес, екі тәуелсіз айнымалысы бар дифференциалдық теңдеулердің
негізгі теориялық мәліметтерін зерттеу және жүйелеу, сондай-ақ
жаратылыстану-ғылыми пәндер циклы бойынша берілген дербес туындылы сызықтық
дифференциалдық теңдеулерді шешу және ол әдістерді сызықтық интегралдық
теңдеулер теориясын зерттеу үшін қолдану мүмкіндігін қарастыру.
Қойылған мақсатқа жету дербес есептердің шешімімен байланысты: бірінші
және екінші ретті дербес туындылы сызықтық дифференциалдық теңдеулердің
негізгі теориясын бейнелеу және математикалық физика теңдеулері мен
сызықтық интегралдық теңдеулер есебін шешудің кейбір амалдарын қарастыру.
Зерттеудің әдістері функционалдық, салыстырмалылық және
сәйкестендіргіштік принциптерінің математикалық құбылыстарды зерттеулеріне
сүйенеді.
Практикалық маңыздылығы: жұмыс теориялық сипатта болып табылады.
Қарастырылған әдістер математикалық физика теңдеулерінің көптеген есептерін
шешу барысында қолданылуы мүмкін.
Жұмыстың жаңалығы дербес туындылы сызықтық дифференциалдық теңдеулердің
кейбір мысалдарымен шешілетін жеткілікті мөлшердегі күрделі материалды
зерттеу болып табылады.
Жұмыста материалдың келесідей орналасу схемасы қабылданған.
Берілген зерттеудің құрылымы кіріспеден, екі негізгі теориялық, үшінші
-практикалық бөлімнен, қорытындыдан және қолданылған әдебиеттер тізімінен
тұрады.
- Бірінші бөлімінде бірінші ретті және екінші ретті дербес туындылы
сызықтық дифференциалдық теңдеулердің түрлері мен классификациясы
қарастырылады, сондай-ақ элипстік типті теңдеулердің негізі
теориясы беріледі.
- Екінші бөлімінде сызықтық интегралдық теңдеулер теориясының
элементтерінен тұрады, оның ішінде қысып бейнелеу әдісі және оның
қолданылуы, Фредгольм теориясы және бірінші текті сызықтық
интегралдық теңдеулер қарастырылады.
- Үшінші бөлімінде бірінші ретті және екінші ретті дербес туындылы
сызықтық дифференциалдық теңдеулер көмегімен шешілетін есептер
қарастырылады.

Қорытындыда жүргізілген зерттеу жұмысының нәтижелерінің қорытындысы
келтіріледі.
Қолданылған әдебиеттер тізімінің саны - 20.

1 Дербес туындылы сызықтық дифференциалдық теңдеулер
туралы түсінік
1.1 Бірінші ретті дербес туындылы сызықтық дифференциалдық
теңдеулер және оларды шешу

І. Біртекті сызықтық теңдеу
Егер бірінші ретті дербес туындылы теңдеулерде
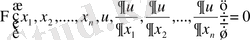(1)
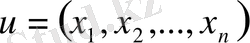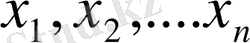- айнымалыларынан тәуелді ізделінді функцияның дербес
туындылары сызықты болып кірсе, онда мұндай теңдеу сызықты деп аталады және
мына түрде жазылады:
(2)
Егер теңдеудің оң жағындағы нөлге теңбе тең, ал
коэффициенттері (яғни ізделінді функциядан) анымалысынан тәуелсіз
болған жағдайда, онда (2) сызықтық теңдеу келесі түрге ие болады
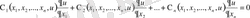(3)
және біртекті деп аталады. Кері жағдайда оны біртексіз деп атайды. Сонымен,
келесі теңдеулерді
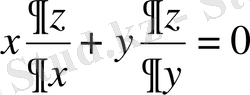(4)
біртекті, ал
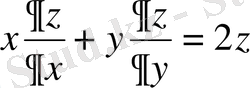(5)
және
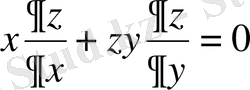(6)
теңдеулерін біртексіз деп атаймыз, мұндағы .
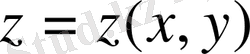Біртекті (3) теңдеуді қарастырайық. 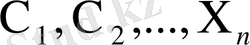өзінің дербес туындыларымен
бірге 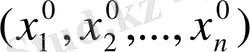бастапқы нүктелерінің кейбір аумақтарының барлық аргументтері
бойынша анықталған және үзіліссіз және де осы нүктеде бір мезгілде нөлге
айналмайды деп болжайық. Мысалға, алсақ,
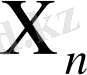
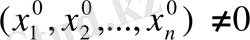. (7)
Біз (3) теңдеуінің шешімін табу туралы сұрақты қарастырамыз, көрсетілген
нүктенің кейбір аумақтарында , яғни (3) теңдеуін теңбе-теңдіке айналдыратын
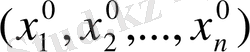, нүктесінің аумағында анықталған және үзіліссіз дифференциалданған
функцияларды іздейміз.
Ең алдымен айтып кететініміз, (3) біртекті теңдеу келесі түрдегі шешімге
ие болады:
(8)
мұндағы . Мұндай шешімдерді айқындалған деп атайды. (3) теңдеудің
коэффициенттеріне қатысты жасалған болжамдардан ол шексіз көп айқындалмаған
шешімдері бар екенін көреміз.
2. Симметриялық формадағы қарапайым дифференциалдық теңдеулер жүйесін
қарастырайық
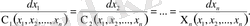(9)
Бұл жүйе (3) дербес туындылы біртекті сызықтық теңдеуге сәйкес,
симметриялық түрдегі қарапайым дифференциалдық теңдеулер жүйесі деп
аталады.
Теорема. 1) Егер 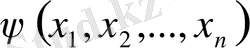функциясы (9) теңдеулер жүйесінің үзіліссіз
дифференциалданатын интегралы болса, онда 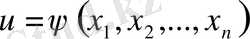(3) теңдеудің шешімі болып
табылады;
2) Егер (3) теңдеудің шешімі болса, онда 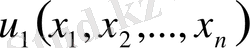(9) жүйенің интегралы
болады.
3. Жасалынған болжамдар бойынша (9) жүйе тура тәуелсіз
интегралдарға ие
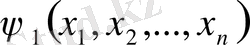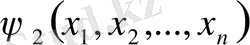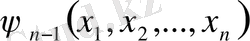, ,...,, (10)
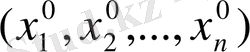бастапқы нүктесінің кейбір аумақтарында үзіліссіз дифференциалданады
және анықталған, себебі бұл болжамдарда (9) жүйе нормальді жүйесінің
теңдеуіне теңбе-тең
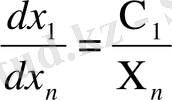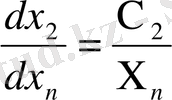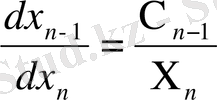, ,..., (11)
(10) интегралдан кез келген үзіліссіз дифференциалданатын функция
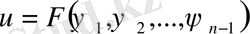(12)
сондай-ақ (9) жүйенің де интегралы болатынын және сәйкесінше, (3)
теңдеуінің шешімі болатынын көреміз.
Екі тәуелсіз айнымалының жағдайын да (3) теңдеуді келесі түрде
қарастырамыз:
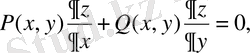(13)
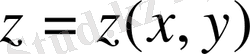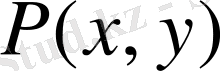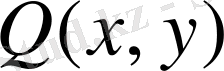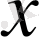мұндағы белгісіз функция, ал және - және 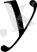-тен
берілген функциялар.
Қарастырылып отырған жағдайда (9) жүйе бір теңдеуге бейнеленеді
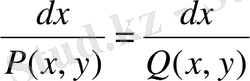. (14)
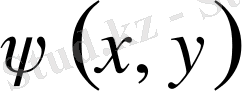- осы теңдеудің интегралы болса, онда (10) теңдеудің жалпы шешімі
келесі түрде болады
, (15)

мұндағы 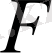- кез келген үзіліссіз дифференциалданатын функция.
ІІ. Біртексіз сызықтық теңдеу
4. Біртексіз сызықтық теңдеуді қарастырайық
(16)
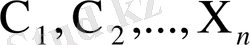коэффициенттері және оң жағы 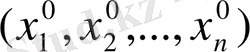бастапқы нүктесінің
кейбір аумақтарында тербес туындысымен бірге анықталған және үзіліссіз деп
болжайық, және де
(17)
(16) теңдеуінің шешімін айқын емес түрде іздейміз
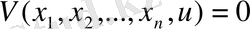, (18)
мұндағы - кейбір өзінің аргументтерінен үзіліссіз дифференциалданатын
функция
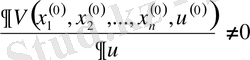. (19)
(4) теңдеуімен анықталатын, функциясын 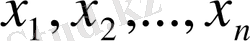тәуелді деп есептеп,
(18) қатынасын қатысты дифференциалдасақ
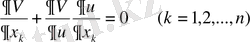, (20)
табамыз, осыдан
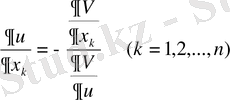. (21)
(21)-ді (16)-ға қоя отырып, 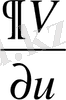-ға көбейтіп және барлық мүшелерін сол
жаққа көшіретін болсақ, келесіні аламыз
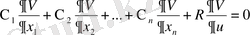(22)
(22) теңдеуі 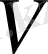ізделінді функциясы бар біртекті сызықтық теңдеу. Оған
сәйкес жүйе симметриялық формада
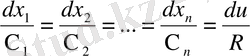(23)
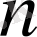тәуелсіз интегралдарға ие
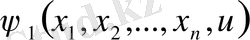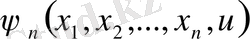,..., (24)
Сол себепті
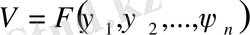(25)
(22) теңдеудің жалпы шешімі болады.
(25)-ті (18)-ге қоя отырып, (16) теңдеуінің ізделінді шешімін келесі түрде
аламыз
(26)
Бұл қатынасты, мұндағы 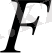-кез келген үзіліссіз дифференциалданатын
функция, (1) теңдеуінің жалпы шешімі деп атаймыз. Егер (26) теңдеуін -
ға қатысты фактілі түрде шеше алсақ, онда жалпы шешімді айқын түрде аламыз
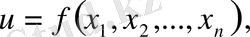(27)
мұндағы - кез келген үзіліссіз дифференциалданатын функция.
Екі айнымалысы бар жағдайда келесі теңдеуді аламыз
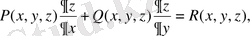(28)
мұндағы . (23) жүйесі келесідей түрде болады
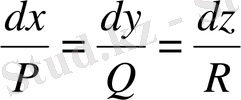. (29)
Егер 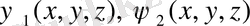- осы жүйенің тәуелсіз интегралдары болса, онда (28) теңдеуінің
жалпы шешімі келесідей түрде болады
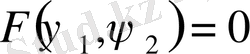. (30)
ІІІ. Сызықтық емес теңдеулер
5. Екі тәуелсіз айнымалысы бар жағдайдағы дербес туындылы бірінші текті
сызықтық емес теңдеуді қарастырамыз
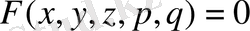, (31)
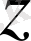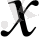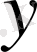мұндағы - және тәуелді ізделінді функция; 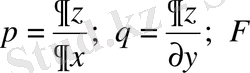- және
тәуелді сызықты емес, 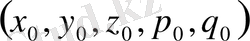бастапқы нүктелерінің кейбір аумағында
өзінің аргументтерінде берілген үзіліссіз дифференциалданатын функция.
Айтып өтетін жайт, (31) түріндегі бір теңдеуді интегралдау есебі, осындай
түрдегі сәйкес екі теңдеулер жүйесін интегралдаудан қиынырақ болады, яғни
алынғаншешім, екі теңдеу жүйесіне де ортақ шешім болады.
Мына жүйені қарастырайық:
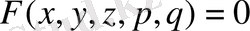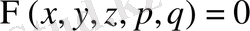; . (32)
Осы жүйені және -ға қатысты оны шешкенде келесіні алуға болады:
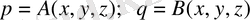, (33)
мұндағы 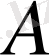және 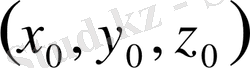бастапқы нүктелерінің кейбір аумақтарында
үзіліссіз дифференциалданады.
(33) жүйесінің қажетті сәйкестік шартын табамыз. 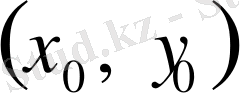бастапқы нүктесінің
кейбір аумақтарында осы жүйенің әрбір теңдеуін қанағаттандыратын және
үзіліссіз дербес туындылары 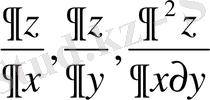бар болады, 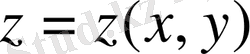функциясы бар деп
болжайық. 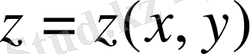деп ойлап, және бойынша (33) теңдеуін
дифференциалдасақ, келесіні аламыз
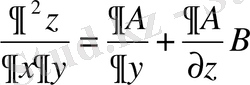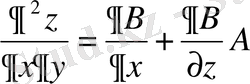; . (34)
Осыдан алатынымыз,
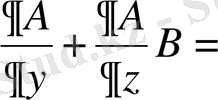
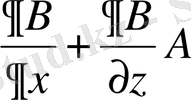
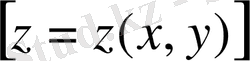(35)
(5) шарты (3) жүйесінің қажетті сәйкестік шарты болып табылады.
(3) жүйесі тек сәйкестік қана болмауы үшін, ең болмағанда кез келген
тұрақтыдан тәуелді,бірақ шешімдер үйірі де бар болуы керек, шарт қажетті
түрде
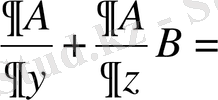
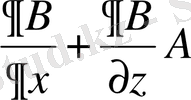(36)
қарастырылып отырылған облысыта 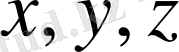қатысты теңбе-теңдік орындалуы керек.
Егер (36) шарт 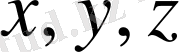-ке қатысты теңбе-теңдік орындалса, онда ол (33)
жүйенің толық интегралдық шарты деп аталады.
6. Пфафф теңдеуі деп келесі түрдегі теңдеу аталады
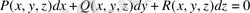. (34)
Бұл теңдеуге барлық 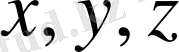айнымалылары симметриялы түрде кіреді, және
олардың әрқайсысын ізделінді функция деп ойлауға болады. 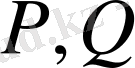және
коэффициенттері өзінің дербес туындыларымен бірге 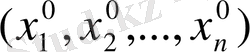бастапқы
нүктелерінің кейбір аумақтарының барлық аргументтері бойынша анықталған
және үзіліссіз және де осы нүктеде бір мезгілде нөлге айналмайды деп
болжайық. Мысалы, былай деп алайық,
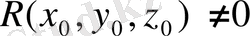. (35)
Онда (34) теңдеуді келесі түрде жазуға болады
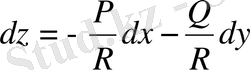. (36)
Кез келген бір тұрақтыдан тәуелді, Пфафф теңдеуінің шешімдері үйірі бар
болатын, шартты табайық. Себебі 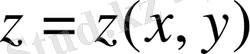кез келген интегралдық бетте негізі
қатынас орындалуы қажет
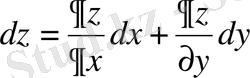(37)
онда интегралдық беттер үшін алатынымыз
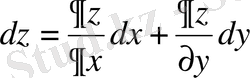
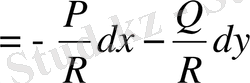, (38)
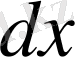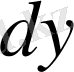және тәуелсіздігінін нәтижесінде алатынымыз, ізделінді
интегралдық беттер теңдеулер жүйесін қанағаттандыруы қажет
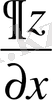
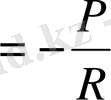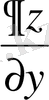
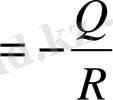; (39)
(34) Пфафф теңдеуі (39) жүйесіне теңгерілген. Нәтижесінде (39) жүйені толық
интегралданатын шарттарын табуға әкеп соғады.
Жүйе үшін
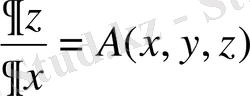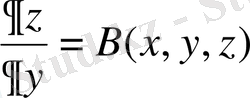; (40)
толық интегралдық шарт келесідей түрге ие
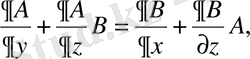(41)
және ол қарастырылып отырған облыста теңбе-тең орындалуы керек. (39)
жүйесіне (41) шартын жаза отырып, алатынымыз
(42)
Екі жағын да 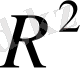көбейтеміз және және мүшелерін жинаймыз
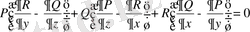. (43)
(43) шартын ыңғайлық үшін келесі түрдегі теңдік түрінде жазуға болады
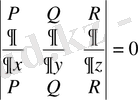. (44)
Егер (43) шарты теңбе-тең орындалса, онда ол Пфафф теңдеуінің толық
интегралданатын шарты деп аталады. (43) шарты орындалғанда Пфафф теңдеуі
(39) жүйесінің интегралдануына келтіріледі. Сонымен қатар бір кез келген
тұрақтысы бар болатын, шешімдер үйірі табылады.

1.2 Екінші ретті дербес туындылы сызықтық дифференциалдық
теңдеулер және оларды шешу

І. Екі тәуелсіз айнымалысы бар дифференциалдық теңдеулер.
Қажетті анықтамаларды берейік.
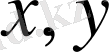екі тәуелсіз айнымалысы бар 2-ретті дербес туындылы теңдеу деп
белгісіз функциясының арақатынасымен және оның 2-ретті дербес
туындыларын қоса алғанда берілетін теңдеуді атаймыз,
.
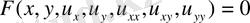мұндағы
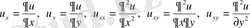
Теңдеу жоғарғы туындыларына қатысты сызықты деп аталады, егер ол келесідей
түрге ие болса
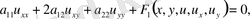(45)
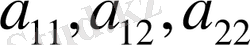
мұндағы және функциясы болып табылады.
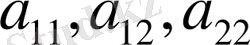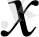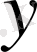Егер коэффициенттері тек қана және тәуелді емес болса, ал
ұқсас болып келсе, функциялары 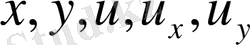, онда мұдай теңдеуді
квазисызықты деп атайды.
Теңдеу сызықты деп аталады, егер ол 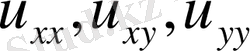жоғарғы туындыларына қатысты
сызықты, дәл солай функциясына және оның бірінші туындылары
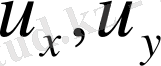қатысты болса:
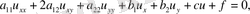(46)
мұндағы 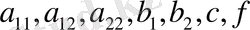- тек және функциялары. Егер (46) теңдеуінің
коэффициенттері және тәуелді емес болса, онда ол тұрақты
коэффициентті сызықты теңдеу болады. Теңдеу біртекті деп аталады, егер
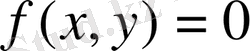болса.
Айнымалыларды түрлендіру көмегімен

кері түрлендіруді болдыратын, біз берілгенге эквивалентті, жаңа теңдеу
аламыз. Сәйкесінше келесі сұрақты қоя аламыз: және
айнымалыларындағы теңдеулер мейлінше қарапайым формада болу үшін оны қалай
аламыз?
Бұл пунктте біз біз теңдеу үшін қойылған сұраққа жауап береміз, және
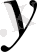екі тәуелсіз айнымалысы бар (45) түрінің сызықты жоғарғы туындыларына
қатысты

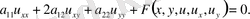
Туындыларды жаңа айнымалыларға түрлендіре отырып, алатынымыз:
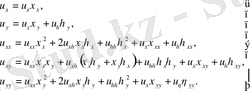(47)
(47) теңдеуінен (45) теңдеуіне туындылардың мәндерін қоя отырып, келесіні
аламыз:
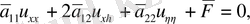(48)
мұндағы

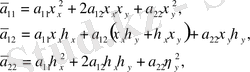
ал функциясы екінші туындыларынан тәуелді емес. Ескере кететіні, егер
де берілген теңдеу сызықты болса,яғни

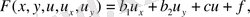
онда келесі түрге ие

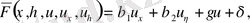
яғни теңдеу сызықты болып қалады.
және айнымалыларын 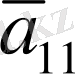коэффициенті нөлге тең болатындай етіп
таңдап аламыз. 1-ретті дербес туындылы теңдеуді қарастырамыз
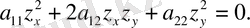(49)
осы теңдеудің қандай-да бір дербес шешімі болсын. Егер деп
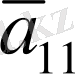ойласақ, онда коэффициенті сәйкесінше нөлге тең болады. Осылайша,
жоғарыда атап өтілген жаңа тәуелсіз айнымалыларды таңдау туралы есеп (49)
теңдеуінің шешімімен байланысты.
Келесі леммаларды қарастырайық.
1. Егер 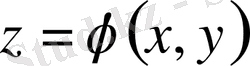келесі теңдеудің дербес шешімі болса

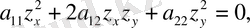
онда 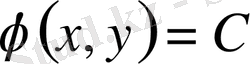қатынасы қарапайым дифференциалдық теңдеудің жалпы интегралы
болып табылады
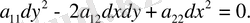(50)
2. Егер 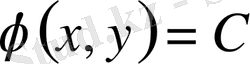қарапайым дифференциалдық теңдеудің жалпы интегралы болып
табылса

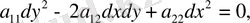
онда 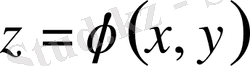функциясы (49) теңдеуін қанағаттандырады.
(50) теңдеуі (45) теңдеуі үшін характеристикалық деп аталады, ал оның
интегралдары-характеристикалар деп аталады.
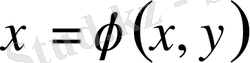деп ойлап, мұндағы 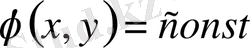(50) теңдеуінің жалпы интегралы, біз
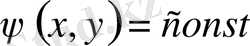
бойынша коэффициентті нөлге айналдырамыз. Егер 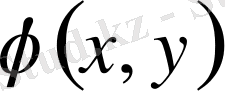тәуелсіз (50)
теңдеуінің басқа жалпы интегралы болып табылса, онда 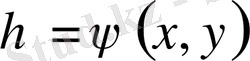деп ойлап, біз
бойынша коэффициентті де нөлге айналдырамыз.
(50) теңдеуі екі теңдеуге бөлінеді:

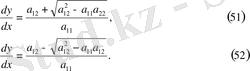
Түбір астындағы берілу белгісі теңдеудің типін анықтайды
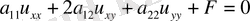. (45)
Бұл теңдеуді біз нүктесіндегі теңдеу деп атаймыз
гиперболалық тип, егер нүктесінде ,
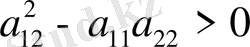эллипстік тип, егер нүктесінде ,
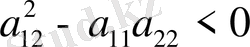параболалық тип, егер нүктесінде .
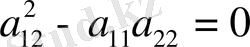ІІ. Көп тәуелсіз айнымалысы бар 2-ретті теңдеудің классификациясы. Нақты
коэффициенттері бар сызықты теңдеуді қарастырайық
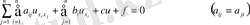, (53)
мұндағы функциясы болып табылады. Жаңа тәуелсіз айнымалы
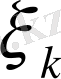енгіземіз,

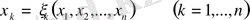
деп ойлаймыз.
Онда

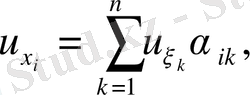
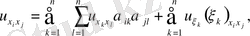
мұндағы
.
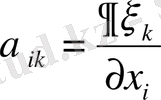Берілген теңдеудің туындыларына өрнекті қоя отырып, алатынымыз:

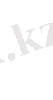
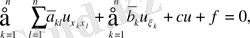
мұндағы

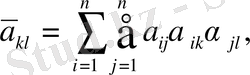
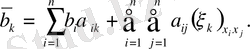
Квадраттық форманы қарастырайық
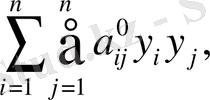(54)
оның коэффициенттері берілген теңдеудің кейбір 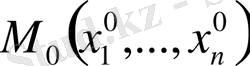нүктелеріндегі
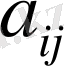коэффициенттеріне тең. 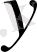айнымалыларына сызықты түрлендіру жасай отырып
,
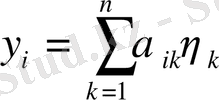квадраттық форма үшін жаңа өрнек аламыз
,
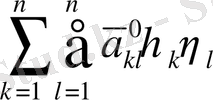мұндағы
.
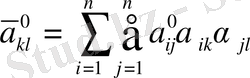Осылайша, теңдеудің негізгі бөлігінің коэффициенттері сәйкес сызықтық
түрлендірудегі квадраттық форманың коэффициенттеріне өзгереді.
ІІІ. Тұрақты коэффициенттері бар сызықтық теңдеудің канондық формасы.
Екі тәуелсіз айнымалысы бар жағдайда тұрақты коэффициенттері бар 2-ретті
сызықтық теңдеу келесі түрге ие болады
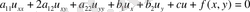. (55)
Оған тұрақты коэффициентті характеристикалық теңдеу сәйкес келеді. Сол
себепті характеристикалар түзу сызықты болады
, .
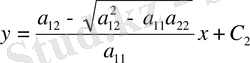Сәйкесінше айнымалыларды түрлендіру көмегімен (55) теңдеу қарапайым бір
формаға келтіріледі:
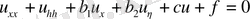(эллипстік тип), (56)

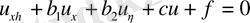
немесе
(гиперболалық тип), (57)

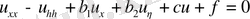
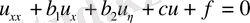(параболалық тип).
(58)
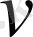Келешекте жеңілдету үшін орнына жаңа функция енгіземіз:
,
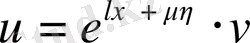мұндағы 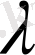және 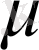- әлі анықталмаған тұрақтылар. Онда

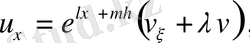
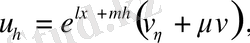
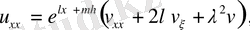
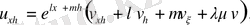
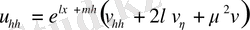
(56) теңдеуінің туындыларына өрнеті қоя отырып және содан кейін
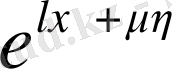қысқарта отырып, алатынымыз:
.
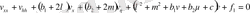және параметрлерін, екі коэффициент, мысалы бірінші
туындыларда, нөлге айналатындай 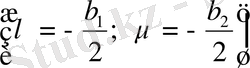етіп таңдап аламыз. Нәтижесінде
алатынымыз:

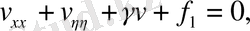
мұндағы 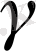- 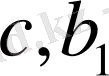және 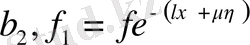арқылы өрнектелетін тұрақты. (57) және (58)
жағдайларына да сәйкес операцияларды жүргізе отырып, келесі тұрақты
коэффициенттері бар канондық формаларға келтіреміз:
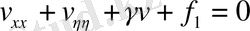(эллипстік тип),
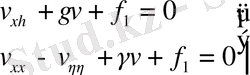(гиперболалық тип),
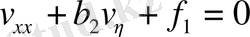(параболалық тип).

1.3 Эллипстік типті теңдеулер

І Гармониялық функциялар және оның қасиеттері
Эллипстік типті теңдеулердің ішіндегі ең қарапайымы Лаплас теңдеуі. Бұл
теңдеу стационарлы құбылыстарды (уақытқа байланыссыз) зерттеуге
қолданылады. Жазықтық үшін Лаплас теңдеуі :
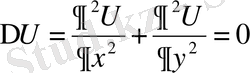(60)
Кеңістікте:
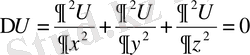(61)
Жазықтықтағы U(x,y), кеңістіктегі U(x,y,z) функциялары үзіліссіз бірінші
және екінші ретті дербес туындыларға ие болып, сәйкесінше (60) және (61)
Лаплас теңдеулерін қанағаттандырса, онда бұл функцияларды гармониялық
функциялар деп аталады Гармониялық функциялардың ең қарапайымы жазықтықтағы
U=ax+by+c, кеңістіктегі U=ax+by+cz+d сызықтық функциялар болып табылады.
(60) және (61) Лаплас теңдеуінің, әсіресе, полярлы, сфералы және цилиндрлік
координаталармен берілген түрі өте жиі қолданылады.
Лемма: U= функциясы, мұндағы r=PP0 - қашықтық P0 нүктесінен
басқа
нүктелердің бәрі де гармониялық функция болады.
Дәлелдеуі:
Берілген функцияның бірінші және екінші ретті дербес туындыларын тауып,
Лаплас теңдеуіне қойып, функцияның гармониялық болатындығына көз
жеткізуге болады.
y

. P P(x,y)
P0(x,-y)
x
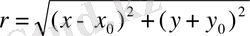
0

.
P0

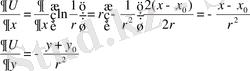
U= 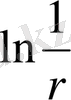функциясы Лаплас теңдеуінің фундаменталды шешімі деп аталады.
Қасиеттері:
10. Орта мән туралы теорема.
Теорема : 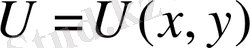функциясы центрі 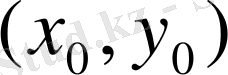нүктесі радиусы R болатын
кейбір D дөңгелегінде гармониялық функуция және D тұйық облыста
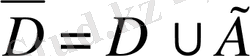
үзіліссіз болсын. Сонда U функциясының дөңгелек центрдегі мәні келесі
формула арқылы анықталады:
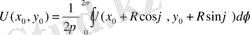(60)
Орта мән туралы теоремада басқа түрде жазуға болады. Ол үшін (60) формуланы
кез келген 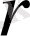радиусты (0≤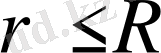) дөңгелек үшін жазайық:
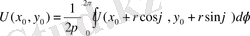(61)
Алынған (61) – формуланың екі жағын да -ге көбейтіп, бойынша
(0,R) аралықта интегралдайық:

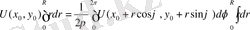
немесе 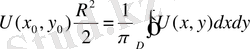, D – радиусы R-ге тең дөңгелек.
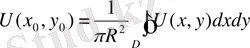(62)
(62) формуланың оң жағы 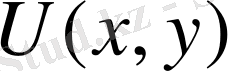гармониялық функцияның радиусы R болатын
дөңгелектегі орта мән.
2.0 Харнак теңсіздігі.
Центрі 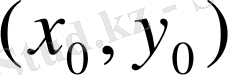нүктесі радиусы R болатын кез келген дөңгелекке 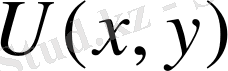≥0
гармониялық функция оң және D тұйық облыста үзіліссіз болсын. Сонда 0≤ ρ≤R
теңсіздігін қанағаттандыратын ρ үшін келесі теңсіздік орындалады:
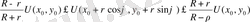(63)
(63) – теңсіздігі Харнак теңсіздігі деп аталады. Харнак теңсіздігінен
Лиувиль теоремасы шығады.
Теорема : Барлық жазықтықта гармониялық функция U тұрақты болмаса,
онда ол жоғарғыдан да, төменнен де шектелген бола алмайды.
Дәлелдеуі: Егер функциясы жоғарыдан шектелген болса, онда
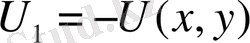функциясы төменнен шектелген болады. Әрі гармониялық функция
болады. Сондықтан да функцияның төменнен шектелгендігін қарастырсақ, сол
жеткілікті
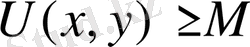
Шынында да 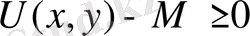оң, әрі гармониялық. Сонымен барлық жазықтықта
гармониялық және оң функциялар әр уақытта тұрақты болады. (63) түрдегі
теңсіздікті пайдаланып, келесі теңсіздікті аламыз:

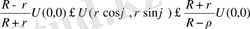
Жазықтықтағы гармониялық функция U үшін ρ тұрақтысын тағайындап және
үлкен R-ді шексіз үлкейтіп, келесі теңсіздікке келеміз:

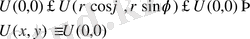
30. Максимум принципы.
Егер 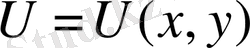функциясы шектелген D облысында гармониялық және облысында
үзіліссіз болса, онда келесі түрдегі теңсіздік орындалады:
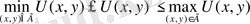(64)
ІІ Грин формулалары
Үлкен D үш өлшемді кеңістігіндегі бағыты анықталған S бетімен шектелген
ақырлы облыс болсын. Сонымен қатар 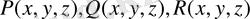функциялары D облысының ішінде
үзіліссіз және шектелген. Сонымен қатар бірінші ретті дербес туындылары бар
болсын. Сонда математикалық анализ курсынан белгілі Остроградский формуласы
орындалады
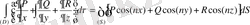(65)
мұндағы n – S бетіне бағыттылған сыртқы нормаль.
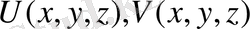функциялары және олардың бірінші ретті дербес туындалары D облысынан S
бетіне дейін үзіліссіз болсын. Ал екінші ретті дербес туындылары D
облысының ішінде үзіліссіз және шектелген болсын.
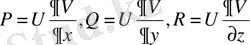деп алып, (65) түрдегі Остроградский формуласын пайдаланып,
келесі формулаға келеміз:
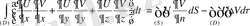(66)
алынған (66) формуланы Гриннің бірінші формуласы деп аталады.
(66) формулада U және V функцияларының орындарын ауыстырып келесі формулаға
келеміз:
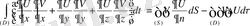(67)
(66)-(67):

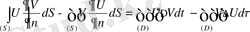
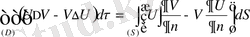(68)
(68) формуланы Гриннің екінші формуласы деп аталады.
ІІІ Лаплас теңдеуі үшін негізгі есептердің қойылымы
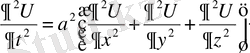(69)

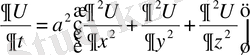(70)
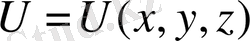функциясы үшін 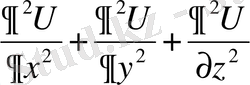=0 орындалады.
Бұл теңдеу бізге белгілі Лаплас теңдеуі немесе
ΔU=0 (71)
деп жазуға болады. Бұл теңдеу уақытқа байланыссыз құбылыстардың күйін
зерттейді.
Егер (71) теңдеуі
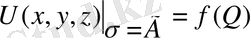(72)
шартын қанағаттандырса, онда мұндай түрде берілген есепті Лаплас теңдеуі
үшін қойылған Дирихле есебі деп аталады.
Ал егер (71) теңдеуі
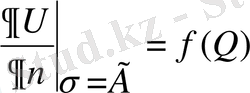(72′)
шартын қанағаттандырса, онда мұндай түрдегі есепті Лаплас теңдеуі үшін
қойылған Нейман есебі деп аталады.
Егер (71) теңдеуі
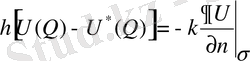(72′′)
шартын қанағаттандырса, онда мұндай түрдегі есепті Лаплас теңдеуі үшін
қойылған үшінші шектік есеп деп аталады.
(72′′) шарттағы h және k тұрақтылары сәйкесінше жылу өткізгіштің ішкі және
сыртқы коэффициенттері болып табылады.
ІҮ Дирихле есебі және оның шешімі
D облысында (71) теңдеуінің (72) түрдегі шартын қанағаттандыратын шешімін
табу.
Теорема: (Дирихле есебі шешімінің жалғыздығы туралы) Лаплас теңдеуі
үшін қойылған Дирихле есебінің шешімі шектелген облыста жалғыз (егер ол бар
болса).
Дәлелдеуі: Кері жоримыз: Дирихле есебінің шешімі
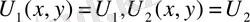
функциялары болсын. Онда 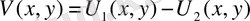функциясы да шектелген D
облысында үзіліссіз және гармониялық функция болып осы облысының
шекарасында нөлге айналады. Ендеше, максимум принципі бойынша келесі
теңдсіздікке келеміз:

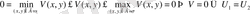
шығады.
Теорема: (Дирихле есебі шешімінің шекаралық шарттан үзіліссіз
тәуелділігі)
U1 және U2 функциялары D облыста гармониялық болсын. Бұл функциялардың
облыс шекарасындағы мәні сәйкесінше f1(Q) және f2(Q) болсын:

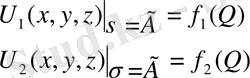
Егер 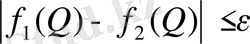теңсіздігі кейбір 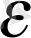үшін орындалса, онда қарастырылып
отырған D облысының барлық жерінде 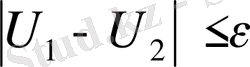орындалады.
Дәлелдеуі: осы функция үшін шарт былай жазылады:

Ендеше, шектелген D облысы үшін
Ү Грин функциясы
Лаплас теңдеуінің жазықтықтағы (кеңістіктегі) түрін қарастырайық:
(71′)
жазықтықтағы нүктелер болсын.

Анықтама: функциясы D облысы үшін Дирихле есебінің Грин
функциясы деп аталады, егер:
1) бұл функция тұйықталған облыста үзіліссіз және D облысының
шекарасында ;
2) бұл функция Р0 нүктесінен басқа нүктелердің бәрінде де
гармониялық;
3) айрым Р0 нүктесінде де гармониялық
шарттарды қанағаттандырса.
Грин функциясын басқаша функцияның көзі деп те атайды. Центрі координата
басы болатын радиусы R –ге тең дөңгелек үшін Грин функциясын қалай құруға
болатынын қарастырайық.
ΔOKP*, ΔOKP0
ΔOKP*~ΔOKP0
(72)
;
, мұндағы r және r1 шамаларын арқылы өрнектейік:

(72) белгілеуді пайдаланып:

Бұл формулаларда r және r1 шамаларының арқылы өрнектелетіндігін
көруге болады. Сонымен
(73)
формуласы дөңгелек үшін Грин функциясы болып табылады. Құрылған (73)
функция үшін анықтамадығы үш шарттың орындалатындығын көрсетуге болады.
Дәл осы сияқты Грин функциясын радиусы R болатын центрі координата басы
болатын шар үшін де құруға болады. (73) түріндегі функциясы шар үшін былай
жазылады:
(73′)

Грин функциясын тек шектелген облыстар үшін емес, шектелмеген облыстар үшін
де құруға болады.
Жарты жазықтық үшін Грин функциясын құрайық.
(73´´)

(73′) функциясы айтылған анықтамадағы үш шартты y0 жарты жазықтығында
қанағаттандырады. Ал y=0 түзуінде . функциясының y0 жарты
жазықтығы гармониялық функция екендігі дербес туындыларды табу арқылы
тікелей дәлелденеді. Шынында да:
- ның гармониялық екенін көреміз. функциясы да
гармониялық болады. Сонымен жарты жазықтық үшін (73″) фукнциясы Грин
функциясы болып табылады екен. Дәл осы сияқты Грин функциясы z0
кеңістігіндегі жарты жазықтық үшін де құруға болады:
(73′′′)
Қорыта айтқанда, Лаплас теңдеуі үшін қойылған негізгі есептерді шешу
барысында ең алдымен бұл есептердің шешімінің жалғыз екендігін, содан кейін
есептердің шешімін табуға міндетті түрде Грин функциясын құру керек. Ал біз
көргендей Грин функциясын құру оңай емес.
ҮІ Дирихле есебін Грин функциясы арқылы шешудің әдістері
Дирихле есебінің шешімін Грин функциясы әдісі арқылы табу бізге белгілі
Грин формулаларына негізделеді. Бұл формула жазықтықта келесі түрде
анықталады:
Егер U және V функциялары өздерінің бірінші ретті дербес
туындыларымен қоса шектелген D облысында үзіліссіз болса, онда
(74)
орындалады. Мұндағы , - Г қисығына жүргізілген сыртқы нормаль
бойынша туынды. (74) формуласы жазықтықтағы Гринннің екінші формуласы болып
табылады. (74) формуласын біле отырып, осы формуладан Гринннің жалпыланған
формуласын шығарып алуға болады:
(75)
мұндағы С- Г қисығының ішінде орналасқан тұйық қисық, D - Г мен С
қисықтарының арасындағы облыс, - С қисығына жүргізілген сыртқы нормаль

Дирихле шартын қанағаттандыратын гармониялық U(x,y) функциясы және
V=G(P,P0) Грин функциясы үшін (75) түріндегі формуланы былай жазуға болады:
(76)
мұндағы С- центрі Р0 нүктесінде орналасқан радиусы - ге тең шеңбер.
(75) формуласында қалған қосындылар нөлге тең, себебі Грин функциясы Г
қисығы үшін . (76) формуласындағы екінші интегралды есептелік. Ол үшін
полярлы координатаға көшеміз.
, ,

Грин функциясының анықтамасынан :

шығады.
Мұндағы D облысының барлық жерінде гармониялық функция. Бұдан
функцияның және оның n1 сыртқы нормаль бойынша алынған туындысының
шектелген болатындығын көреміз. Басқаша айтқанда

Бұдан басқа U және бұл функцияның n1 сыртқы нормаль бойынша туындысы да D
облысында шектелген. Олай болса,
(77)
Бұл формуладағы шектелген өте аз шексіз шамалар.
(77) формуланы екі жағынан да шекке көшіп, Дирихле шартын пайдаланып,
келесі формулаға келеміз:
(78)
Пуасонның интегралдық формуласы.
(78) формула жазықтық үшін Грин формуласы белгілі болғандағы Дирихле
есебінің шешімін табатын формула. (78) арқылы Дирихле есебінің дөңгелек
үшін, дөңгелектің сырты үшін және жарты жазықтық үшін шешімін табуға
болады.
ҮІІ Дөңгелек үшін Дирихле есебі
Есеп: Жазықтықтағы Лаплас теңдеуінің
(79)
келесі шекаралық шартты:
(80)
қанағаттандыратын шешімін тап.
Бұл есебін шешу үшін Лаплас теңдеуін полярлы координаталар арқылы келесі
түрге келтіреді:

Лаплас теңдеуі полярлы координатада:
(81)
(81) теңдеуінің шешімін Фурье әдісі бойынша белгісіз екі функцияның
көбейтіндісі түрінде іздейміз:
(82)
(81)→(82):

,

болғанда (83)

(85)
(84)

(86)
болғанда (83)
(87)
(84)

(88)
функциясы айнымалысына байланысты периодты функция болғандықтан
(85) формуладан В тұрақтысының 0-ге тең екендігі шығады. Ал (87) формулада
k параметрі 1,2,3,... мәндердің біреуін қабылдайды. (86) және (88)
формулалардан функциясының r=0 нүктесінде үзілісті функция
болатындығын көруге болады. Олай болса, центрі координата басында жататын,
радиусы R дөңгелегінде гармониялық бола алмайды. Осыдан
(81)теңдеуінің дөңгелекте шексіз көп дербес шешімі бар болатындығын және ол
шешім келесі түрде:

алынады. Лаплас теңдеуінің сызықтығынан және біртектілігінен шығатын
(89)
(89) түрдегі құрылған функция да осы теңдеудің шешімі болып табылады. (89)
түрде табылған функцияға берілген шектік шарттың орындалатындығын
көрсетейік.

Ал бұл формула функцияның аралығында Фурье қатарына жіктелісін
береді. Мұндағы
, ,
(90)
формулалар арқылы анықталады. Сонымен

Тік жақша ішіндегі өрнекті ықшамдайық:

(91)
(91) формула дөңгелек үшін Дирихле есебінің шешімі болып табылады. Бұл
формуланың оң жағындағы интегралды Пуассон интегралы деп атайды.
функциясын дөңгелек үшін Пуассонның ядросы деп атайды.
Ядро Пуассонының қасиеттері:
1. ρR үшін ядро Пуассоны оң, r=R болғанда нөлге тең.
2. Егер нүктесі дөңгелек ішіндегі айнымалы нүкте болса, онда ядро
Пуассоны гармониялық функция болады.
3. Пуассон ядросы үшін ρR болғанда,

ҮІІІ Дөңгелектің сырты мен жарты жазықтық үшін Дирихле есебі
Центрі координата басында жататын, радиусы R-ге тең дөңгелек
үшін Дирихле есебі былай қойылады:
Жазықтықтағы Лаплас теңдеуінің шекаралық шартты қанағаттандыратын
шешімін табу. Бұл дөңгелектің іші үшін қойылған есебі:
.
Дөңгелектің сырты D1=DUГ үшін Дирихле есебі былай қойылады:
функциясының келесі түрдегі шарттарды қанағаттандыратын шешімін табу
: 1) D1 шектеусіз облыста ;
2) функциясы D1 облысының барлық нүктелерінде үзіліссіз;
3) фукнцмясының дөңгелек шекарасындағы мәні

4) функциясы шексіздікте басқаша айтқанда, D1 облысында шектелген
функция, яғни

D1 облысы үшін Дирихле есебі осылай қойылады.

Теорема: D1 облысы үшін қойылған Дирихле есебінің шешімі жалғыз және
ол шешім шекаралық шарттағы f1(Q) функциясы қалай берілгеніне тәуелді.
D1 облысы үшін қойылған Дирихле есебінің шешімі Пуассонның интегралдық
формуласы арқылы табылады. Бірақ, бұл формулада r және R шамаларының
орындары ауыстырылған.
(91′)
(91′) формуладағы Пуассонның ядросы (91) формуладағы сияқты қасиеттерімен
бірдей.
Жарты жазықтық үшін Дирихле есебі былай қойылады:
Жазықтықтағы
(92)
Лаплас теңдеуінің
(93)
шекаралық шартын қанағаттандыратын шешімін табу.
Жарты жазықтық үшін құрылған Грин функциясын біле отырып, осы жазықтықтағы
функциясын табатын Пуассонның интегралдық формуласын қорытып шығару
қиын емес. Ол үшін Грин формуласының нормаль бойынша туындысын табайық:

,
мұндағы

Егер y=0, онда

(94)
(94) формула жарты жазықтық үшін Дирихле есебінің шешімін табатын формула.

2 Сызықтық интегралдық теңдеулер
2.1 Сызықтық интегралдық теңдеулерді кластарға бөлу

Белгісіз функциялар ингералдардың астында кездесетін теңдеулер
интегралдық теңдеулер деп аталады. Егер белгісіз функция интегралдық
теңдеуге сызықтық түрде қатынасса, онда теңдеуді сызықтық деп атайды.
(95)
түріндегі теңдеу Фредгольмнің 2-текті сызықтық интегралдық теңдеуі деп
аталады. Мұндағы -нақты айнымалы аргументіне тәуелді белгісіз
функция, функциясы кесіндісінде, функциясы
жиынында анықталған белгілі функциялар: пен сәйкес интегралдық
теңдеудің бос мүшесі мен ядросы деп аталады, ал -параметр.
Интегралдық жоғарғы және төменгі шектері ( а мен b) жалпы жағдайда тұрақты
шамалар; олар шектелген де шектелмеген де болуы мүмкін. Егер болса,
онда жоғарыдағы (95) интегралдық теңдеуі біртекті, ал болған жағдайда-
біртекті емес деп аталады.
Фредгольмнің 1-текті интегралдық теңдеуінде белгісіз функция интегралдық
мүшеде ғана қатынасады, дәлірек айтқанда, ол теңдеу

түрінде жазылады.
Вольтерраның 2-текті теңдеуі деп
(96)
түріндегі, ал 1-текті интегралдық теңдеуі деп

түріндегі теңдеуі аталады.
Егер функциясын интегралдық теңдеуге қойғанда теңдеу тепе-теңдікке
айналса, онда функциясы интегралдық теңдеудің шешімі деп аталады.
Интегралдық теңдеудің шешімі бар және оның жалғыз болуы параметріне
байланысты екенін келешекте көрсетеміз. Мәселен, Фредгольмнің біртекті
интегралдық

теңдеуінің параметрінің кез келген мәндерінде шешімі бар
болады, ол 0-ден ерекше шешімдер әрқашан бола бермейді.
Фредгольмнің біртекті интегралдық теңдеуінің 0-ге тең емес шешімдері бар
болатын параметрінің мәндері меншікті мәндер деп, ал оларға сәйкес 0-
ден ерекше шешімдер меншікті функциялар деп аталады.
Ескерту. Вольтерра теңдеуін Фредгольм теңдеуінің дербес түрі деп қарауға
болады. Себебі (96) теңдеуінің ядросы облысында анықталған, ал
жағдайында деп алсақ, онда біз (95) теңдеуінің ядросын

түрінде анықтаймыз.
Бұл ескерту бойынша Фредгольм теңдеуі үшін дәлелденген қасиеттер
Вольтерра теңдеуі үшін де орындалады. Бірақ Вольтерра теңдеуінің тек өзіне
тән ерекше қасиеттері бар, сондықтан Фредгольм теңдеуімен қатар Вольтерра
теңдеуін де қарастырамыз.
Келешекте (95) және (96) интегралдық теңдеулердегі берілген бос мүше
пен ядро үзіліссіз немесе квадраттарымен интегралданатын функциялар:

яғни , деп ұйғарамыз. Осы шартты қанағаттандырушы
функциясын Фредгольм ядросы деп атайды. Фредгольм ядроларына мысалдар
келтірейік.
1-мысал. ядросындағы айнымалылар болғанда фредгольмдік
ядро болады, ал болса, онда ол фредгольмдік ядро болмайды.
Расында
2-мысал. Егер интегралдық теңдеудің ядросы
(97)
мұндағы -үзіліссіз функция және болса, онда ядро фредгольмдік
болады, ал болса, ол ядро фредгольмдік болмайды.
Егер (97) ядросында болса, онда ол ядро ерекшелігі әлсіз немесе
полярлық ерекшелікті ядро деп, ал теңдеу ерекшелігі әлсіз интегралдық
теңдеу деп аталады. Егер болса, онда интегралданбайтын функция
болады. Бұл функциядан алынған интеграл тек Кошидің бас мәні мағынасында
ғана бар болуы мүмкін. Ядросы түріндегі интегралдық теңдеуді
сингулярлық интегралдық теңдеу, ал басқаларын регулярлық интегралдық
теңдеулер деп атайды. Бір аргументті сингулярлық интегралдық теңдеудің
жалпы түрі:

мұнда -комплекс жазықтықтағы тұйық немесе тұйық емес қарапайым доғалар
жиыны; және функциялар доғасында анықталған, ал .
Біз тек сызықтық регулярлық интегралдық теңдеулерді ғана қарастырамыз.
Интегралдық теңдеулерді бір аргументті функция үшін ғана емес, көп
аргументті функциялар үшін де қарастыруға болады.
Мәселен, Фредгольмнің 2-текті интегралдық теңдеуінде ядро ,
бос мүше , ал .
Фредгольмнің 2-текті сызықтық интегралдық теңдеулер жүйесі

түрінде өрнектеледі. Егер -векторлар, ал ядро элементтері
болатын матрица деп қарасақ, онда жүйені (95) теңдеуі түрінде жазуға
болады.
Дәл осындай екі аргументті функция үшін Вольтерра теңдеуі

түрінде, ал жүйені

түрінде өрнектеуге болады.
Математикалық, физикалық кейбір қолданбалы есептерді шешу сызықтық емес
интегралдық теңдеулерді шешуге алып келеді. Сондықтан кейбір практикалық
және теориялық маңызы бар бірнеше сызықтық емес интегралдық теңдеулерді
зерттеусіз келтірейік.
1) Гаммерштейн теңдеуі

мұндағы -фредгольмдік ядро.
2) Урысон теңдеуі

мұндағы -үзіліссіз функция; , ал -шенелген оң шама.
3) Вольтерраның сызықтық емес теңдеуі

мұндағы -үзіліссіз функция, облысында анықталған.
4) Ляпунов-Лихтенштейн теңдеуі

мұндағы мен үзіліссіз функциялар.
Егер теңдеулерде белгісіз функцияның интегралымен қоса туындылары да бар
болса, ондай теңдеулерді интегро-дифференциалдық теңдеулер дейміз. Мысал
үшін мына ең қарапайым интегро-дифференциалдық теңдеулерді келтірейік:
(98)

(99)
мұнда белгісіз функциялардың бірінші ретті туындылары бар болғандықтан, бұл
теңдеулердің шешімі жалғыз болуы үшін қосымша шарттары берілуі қажет.
Қолданбалы математикада интегро-дифференциалдық сызықтық, сызықтық емес
теңдеулер немесе теңдеулер жүйесі және жоғарғы ретті туындылы (кәдімгі және
дербес туындылы) интегро-дифференциалдық теңдеулер көп кездеседі. Мысалы

Теңдеуінің бастапқы шарттарын немесе шекаралық шарттарын
қанағаттандыратын шешімін табу есебін қарастыруға болады. Егер белгісіз
функция көп аргументті болса, онда интегро-дифференциалдық теңдеулерде
белгісіз функциялардың дербес туындылары мен интегралдары көп өлшемді
болады. Интеграл астындағы өрнекте белгісіз функциялардың туындылары
болатын интегро-дифференциалдық теңдеулер де жиі кездеседі. Кейбір
жағдайларда интеграл астындағы туындының реті жоғары болса, ондай
теңдеулердің шешімдері барлық уақытта бола бермейді және шешімнің бар
екенін дәлелденген күнде оны табу оңай емес. Ал еген интеграл сыртындағы
өрнекте белгісіз функциялардың туындылары жоғарғы ретті болса, көп жағдайда
мұндай интегро-дифференциалдық теңдеулерді жүйелерге дифференциалдық және
интегралдық теңдеулердің жүйелерінің жалпы теориясын пайдаланып шешуге
болады.
3-мысал ретінде (98) мен (99) теңдеулерін сызықтық интегралдық
теңдеулерге келтірейік. Ол үшін

деп белгілесек, онда (98) теңдеуінен І-ретті сызықтық дифференциалдық
теңдеуін аламыз. Оның шешімі

Бұл өрнекке -тің мәнін қойсақ,

Мұнда

Белгілеулер енгізсек, онда біз Вольтерраның 2-текті сызықтық

теңдеуін аламыз. Осы әдіспен (99) теңдеуін Фредгольмнің 2- текті сызықтық
интегралдық теңдеуіне келтіруге болады.

2.2 Қысып бейнелеу әдісі және оны қолдану

Алгебралық, дифференциалдық, интегралдық және функционалдық теңдеулердің
шешімдері бар және олар жалғыз болуын дәлелдеуге біртіндеп жуықтау әдісі,
яғни қысып бейнелеу әдісі қолданылады. Қысып бейнелеу әдісінің мазмұнын
төмендегі тұжырымнан білуге болады.
1-теорема (Банахтікі). Толық метрикалық кеңістігінің кез келген
элементін сол кеңістіктің өзіне бейнелейтін операторы берілсін: яғни
. Оның үстіне элементтері
(100)
теңсіздігін қанағаттандырсын (мұндағы саны пен
элементтеріне тәуелсіз және ). Сонда кеңістігінде жалғыз ғана
элементі табылып, ол
(101)
теңдеуін қанағаттандырады.
(100) теңсіздігін қанағаттандыратын операторын қысу операторы деп, ал
(101) теңдеуін қанағаттандыратын нүктесін операторының
қозғалмайтын нүктесі деп атайды.
Дәлелдеуі. элемент алып, мынадай тізбек құрайық: . Осы
тізбегінің фундаментальдық өзіне жинақты екенін көрсетейік. Алдымен

екенін байқаймыз. Егер үшбұрыштар теңсіздігін пайдалансақ,

Осыдан болғандықтан
(102)
Соңғы теңсіздіктен үшін . Демек, тізбегі фундаментальдық
тізбек. кеңістігінің толықтығынан тізбегінің шегі болады:

Енді екенін көрсетейік. Расында , элементі болғандықтан,
санына сәйкес нөмері табылып, болады. Демек, .
Мұндағы кез келген сан болғандықтан , яғни теңдігі орынды.
Қысу операторының қозғалмайтын нүктесінің жалғыз екенін дәлелдейік. Ондай
нүктелер екеу ( және ), яғни , теңдіктері орындалады
деп ұйғарайық. Ол жағдайда . Егер болса, онда болады. Бұл
теорема шартына қайшы, демек, , яғни .
Ескерту. (102) теңсіздіктен жағдайда -жуық шешімдегі қателік

шартымен анықталады. Бұл теңсіздік екінші жағынан тіізбектің жинақтылық
жылдамдығын көрсетеді.
І. Қысып бейнелеу әдісін Фредгольмнің интегралдық теңдеуіне қолдану
1. Интегралдық теңдеудің ядросы үзіліссіз функция болсын.
Фредгольмнің біртекті емес
(103)
теңдеуінің шешімі бар және шешімнің жалғыз екенін дәлелдеуге қысып бейнелеу
әдісін қолданайық. ядросы облысында үзіліссіз болғандықтан
шенелген, яғни . Ал бос мүше - (103) интегралдық теңдеу шешімін
класынан іздейміз. Операторды

деп белгілейік.
1-лемма. интегралдық операторы толық және кеңістігін сол
кеңістіктің өзіне бейнелейді.
Дәлелдеуі. және деп белгілейік, болсын. Ол кезде
және болғандықтан үшін саны табылып, болғанда
теңсіздіктері орындалады. Егер осы теңсіздіктерді алдыңғы өрнектің оң
жағына пайдалансақ, екенін көреміз, яғни функциясы
кесіндісінің кез келген нүктесінде үзіліссіз. Демек операторы кез
келген функциясын тағыда сол кеңістіктегі үзіліссіз функцияға
бейнелейді екен.
Енді -қысу операторы болатын шартты анықтайық.

Міне бұдан

шарты орындалғанда -қысу операторы болатынын көреміз. Жоғарыда
дәлелденген қысып бейнелеу әдісінен, егер саны осы теңсіздікті
қанағаттандырса, онда (103) теңдеуінің бір ғана үзіліссіз шешімі болады. Ол
шешімге жуықтайтын функциялар тізбегі

рекурентті теңдіктермен анықталады, мұндағы функциясы кесіндіде
анықталған кез ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.