Комплекс сандар мен көпмүшелер: негізгі теоремалар, түбірлер және жіктелу


Мазмұны
Кіріспе 3
1 Комплекс сандар4
1. 1 Комплекс сандардың өрісі4
1. 2 Комплекс санның түйіндесі және модулі. 6
1. 3 Комплекс санның тригонометриялық тұлғасы7
1. 4 Комплекс сандарды тригонометриялық тұлғада көбейту және
дәрежеге шығару9
1. 5 Комплекс санның көрсеткіштік тұлғасы. 10
1. 6 Кез келген комплекс санның түбірлері13
2 Көпмүшелер . . . 15
2. 1 Көпмүшелер сақинасының анықтамасы. 15
2. 2 Көпмүшенің дәрежесі. 18
2. 3 Көпмүшені х - х0 екімүшесіне қалдықпен бөлу. Безу теоремасы…. 18
2. 4 Көпмүшенің түбірлері . . . 21
2. 5 Қалдықпен бөлу туралы теорема. . 23
2. 6 Евклид алгоритмі. 25
2. 7 Өрісте жіктелмейтін көпмүшелер. 28
2. 8 Өрістегі көпмүшені жіктелмейтін көбейткіштерге жіктеу. . 29
3. Көпмүшенің жіктелмейтін еселі көбейткіштері және
еселі түбірлері31
3. 1 Көпмүшені x - c айырымының дәрежелері бойынша жіктеу………. 31
3. 2 Көпмүшенің еселі жіктелмейтін көбейткіштері. . 32
3. 3 Көпмүшенің еселі түбірлері . . . 32
4 Комплекс сандар өрісінің алгебралық тұйықтығы . . . 35
4. 1 Алгебраның негізгі теоремасы. . 35
4. 2 Нақты көпмүшенің жорамал түбірлерінің түйіндестігі. 36
4. 3 Рационал бөлшектер . . . 39
4. 4 Үшінші дәрежелі теңдеулер. . 43
4. 5 Нақты кубтық теңдеулер . . . 46
4. 6 Төртінші дәрежелі теңдеулер . . . 48
Қортынды . . . 50
Қолданылған дебиеттер тізімі . . . 51
Кіріспе
Қысқаша тарихи мәлімет
Комплекс сан үғымы тұңғыш рет XVI ғасырда итальяндықтар Дж. Кардано және Р. Бомбелли қарастырған дискриминанты теріс квадрат теңдеулердің, әсіресе кубтық теңдеулердің, шешімдеріне байланысты шыққан ұғым. 1572 жылы шыққан «Алгебра» атты кітабында Р. Бомбёлли комплекс сандарға арифметикалық операциялар колданған.
Алғашкы кезде комплекс сандардың іс жүзінде нақты түрде түсінігі (ин-терпретациясы), болмағандықтан ондай түбірлерді «мүмкін емес», «жорамал» деп санап, ондай түбірлері бар теңдеулерді «түбірі жоқ» теңдеулер қатарына қосатын болған. Комплекс сандардың жан-жақты қолданылуы тек XVIII ға-сырда басталады. Міне осы кезде комплекс сандардың интегралдық есептеуде механикада және геометрияда қолданулары комплекс аргументті функциялар-ды қарауға әкеп соқты. Осы мәселелер жайындағы зерттеулерде туған жері Швейцария болса да, отыз жылдан аса Петербург академиясында жұмыс істеп, өзін «орыс ғалымымын» деп атап өткен Леонард Эйлер (1707-1783) мен француз математигі және философы Даланбердің (1717-1783) үлесі көп.
Комплекс сандарға жазықтықтағы нүкте не вектор деп геометриялық тү-сінікті 1797 жылы даниялық жер өлшеуші К. Вессель (1745-1818) берген,
бірақ тек атақты неміс математигі Карл Фридрих Гаусстың (1777-1855)
комплекс сандарды арифметикаға, алгебраға, геометрия және математикалық анализге қолданған еңбектерінен кейін ғана көпшілік комплекс сандардың геометриялық мағынасын қолданып, оны толық пайдалана бастайды. Ма-тематикаға «комплекс сан» терминін қіргізген де, жоғарғы алгебраның негізгі теоремасының толық дәлелдеуін тұңғыш рет (1799) ұсынған да К. Гаусс.
XIX ғасырдың аяғында жиындар теориясының дамуына байланысты комплекс сан х+іу екі нақты сан х пен у-тің реттелген. пары (х, у) түрінде қаралуы комплекс сандардың геометриялық кескінінен ешбір кем емес екендігі де кейінгі кезде белгілі болып отыр[10] .
Өзектілігі: Комплекс сандар мен көпмүшелер «Алгебра және сандар теориясы » атты жоғары оқу орнындағы пәнінде өтіледі. Мектепті алсақ, осы тақырып математиканы тереңдетіп оқытатын сыныптарда кездеседі.
Мақсаты: Комплекс сандар, олардың қасиеттері, комплекс сандарға қолданатын амалдарын, комплес сандардың геометриялық тұлғасын, көрсеткіштік тұлғасын, көпмүшелердің бөлінгіштігін, Безу теоремасын, көпмүшенің түбірлерін, көпмүшелердің ең үлкен ортақ бөлгішін, алгебраның негізгі теоремасын, кейбір үшінші және төртінші дәрежелі көпмүшелердің түбірлерін анықтаудың жолдарын қарастыру.
Міндеттері: Қарастырылған тақырып бойынша алған білімдерімді мектеп тәжірибиемде қолдану.
- Комплекс сандарКомплекс сандардың өрісі
Анықтама 1. 1. 1 Комплекс сан деп a + bi түріндегі өрнек аталады, мұндағы a , b - нақты сандар және i - жорамал бірлік деп аталатын арнайы символ. Комплекс сандарды басқаша Гаусс сандары деп те атайды.
Комплекс сандар жиыны C деп белгіленеді:
C = { a + bi a , b ∈ R }
Егер екі z 1 = ( a 1 + b 1 i ), z 2 = ( a 2 + b 2 i ) комплекс санға a 1 = a 2 және b 1 = b 2 болса, онда z 1 , z 2 сандары тең деп есептеледі.
0 + 0⋅ i комплекс саны нөлдік комплекс сан деп аталады және 0 деп белгіленеді, 1 + 0⋅ i саны бірлік комплекс сан деп аталады және 1 деп белгіленеді.
Егер z = a + bi комплекс саны берілсе, онда a саны z санының нақты бөлігі , b жорамал бөлігі деп аталады. Олар сәйкесінше Re z және Im z деп белгіленеді.
Жорамал бөлігі нөл болатын комплекс сан, a + 0⋅ i түріндегі сан, нақты a санымен теңестіріледі, ал нақты бөлігі нөл болатын сан, 0 + bi түріндегі сан, таза жорамал сан деп аталады.
Комплекс санын z = a + bi түріндегі жазуы z санының алгебралық тұлғасы деп аталады.
Комплекс сандардың қосындысы
( a 1 + b 1 i ) + ( a 2 + b 2 i ) = ( a 1 + a 2 ) + ( b 1 + b 2 ) i
және көбейтіндісі
( a 1 + b 1 i ) ( a 2 + b 2 i ) = ( a 1 b 1 - b 1 b 2 ) + ( a 1 b 2 + a 2 b 1 ) i
формулаларымен анықталады.
Көбейту формуласынан i 2 = i ⋅ i = (0 + 1⋅ i ) (0 + 1⋅ i ) = -1 екені шығады. Сөйтіп, i 2 = -1.
Теорема 1. 1. 1 Комплекс сандардың C жиыны анықталған қосу және көбейту операцияларына қатысты өріс құрайды.
Дәлелдеу . Комплекс сандардың C жиыны анықталған қосу және көбейту операцияларына қатысты коммутатив сақина құрайтынын Гаусс сандарға сияқты дәлелдеуге болады.
Нолден өзгеше
z
=
a
+
bi
комплекс саны берілсін. Онда
a
≠ 0 немесе
b
≠ 0, сондықтан
a
2
+
b
2
≠ 0. Енді
z
санын
 =
a
+ (-
b
)
i
санына көбейтейік:
z
⋅
=
a
+ (-
b
)
i
санына көбейтейік:
z
⋅
 =
=
(
a
+
bi
) (
a
-
bi
) =
a
2
+
b
2
. Осыдан
z
-1
=
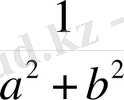 (
a
-
bi
) =
(
a
-
bi
) =
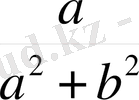 +
+
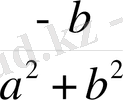 i
. Сөйтіп, кез келген нөлден өзгеше
z
=
a
+
bi
комплекс санына кері комплекс сан табылады. Сондықтан комплекс сандар жиыны өріс құрайды.
i
. Сөйтіп, кез келген нөлден өзгеше
z
=
a
+
bi
комплекс санына кері комплекс сан табылады. Сондықтан комплекс сандар жиыны өріс құрайды.
Анықтама 1. 1. 2 Сандар өрісі деп өзі өріс болатын комплекс сандар өрісінің кез келген і-ші жиыны аталады.
Сан ұғымы қазір былай кеңейтіледі. Әуелі натурал сандар N = {1, 2, …} жиынында қосу және көбейту операциялары беріледі. Одан кейін бүтін сандар Z сақинасы натурал сандар жиынын қамтитын ең кіші сақина деп анықталады. Одан кейін рационал сандардың Q өрісі бүтін сандар сақинасын қамтитын ең кіші өріс деп анықталады. Атап айтқанда, рационал сандар өрісі бүтін сандар сақинасының бөлінділер өрісі болады. Енді нақты сандар рационал сандардан құралған жинақталатын тізбектердің шектері деп анықталады. Ол математикалық анализ курсында қаралады.
1-теоремада нақты сандар өрісі комплекс сандар С өрісіне дейін кеңейтілді. Сөйтіп, сан ұғымының дамуын N ⊆ Z ⊆ Q ⊆ R ⊆ C тібекшемен көрсетуге болады. Ал сан ұғымын одан әрі кеңейтуге бола ма деген сұрақ туады. XIX ғасырда ағылшын математиктері Гамильтон мен Кэли комплекс сандар өрісін екі түрде ғана кеңейтуге болады. Бірінші жол кватерниондар K 4 денесіне дейін, екінші жол Кэли алгебрасына немесе октавалар алгебрасына деп аталатын алгебраға дейін. Кеңейтілсе де, кватерниондарға көбейту коммутатив операция болмайды, ал октаваларға көбейту коммутатив және ассоциатив операция болмайды [1] .
- Комплекс санның түйіндесі және модулі
Анықтама
1. 2. 1 Комплекс
z
=
a
+
bi
саны үшін
 =
a
-
bi
саны
түйіндес сан
деп аталады.
=
a
-
bi
саны
түйіндес сан
деп аталады.
z
пен
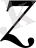 бір-біріне түйіндес екенін көруге болады.
бір-біріне түйіндес екенін көруге болады.
Анықтама
1. 2. 2
z
=
a
+
bi
саны үшін
z
=
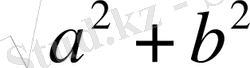 шамасы
z
санының
модулi
деп аталады.
шамасы
z
санының
модулi
деп аталады.
Теорема Кез келген комплекс z , z 1 , z 2 сандары үшін келесі қасиеттер орындалады.
1)
 =
=
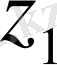 +
+
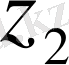 ;
;
2)
 = -
= -
 ;
;
3)
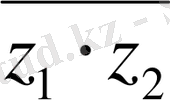 =
=
 ⋅
⋅
 ;
;
4)
z
∈
R
болғанда, сонда ғана
 =
z
болады;
=
z
болады;
5)
z
⋅
 =
z
2
;
=
z
2
;
6) z ≥ 0 және z = 0 болғанда, сонда ғана z = 0;
7)
 =
=
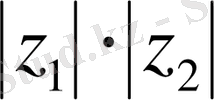 ;
;
8) z 1 + z 2 ≤ z 1 + z 2 (үшбұрыш теңсіздігі) ;
9) z 1 - z 2 ≤ z 1 - z 2 ≤ z 1 + z 2 .
Дәлелдеу . z = a + bi , z 1 = a 1 + b 1 i , z 2 = a 2 + b 2 i болсын.
1.
 =
=
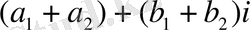 (
a
1
+
a
2
) - (
b
1
+
b
2
)
i
= (
a
1
-
b
1
i
) + (
a
2
-
b
2
i
) =
(
a
1
+
a
2
) - (
b
1
+
b
2
)
i
= (
a
1
-
b
1
i
) + (
a
2
-
b
2
i
) =
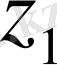 +
+
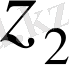 .
.
2. Анықтама бойынша,
 =
a
-
bi
, -
=
a
-
bi
, -
 = (-
a
) +
bi
. Одан әрі -
z
= -(
a
+
bi
) = (-
a
) + (-
b
)
i
. Осыдан
= (-
a
) +
bi
. Одан әрі -
z
= -(
a
+
bi
) = (-
a
) + (-
b
)
i
. Осыдан
 = (-
a
) - (-
b
)
i
= (-
a
) +
bi
. Сондықтан
= (-
a
) - (-
b
)
i
= (-
a
) +
bi
. Сондықтан
 = -
= -
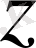 .
.
3. Бір жағынан
 =
=
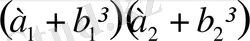 =
=
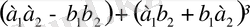 = (
a
1
a
2
-
b
1
b
2
) - (
a
1
b
2
+
b
1
a
2
)
i
. Екінші жағынан
= (
a
1
a
2
-
b
1
b
2
) - (
a
1
b
2
+
b
1
a
2
)
i
. Екінші жағынан
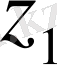 ⋅
⋅
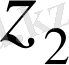 = (
a
1
-
b
1
i
) ⋅ (
a
2
-
b
2
i
) = [
a
1
a
2
- (-
b
1
) (-
b
2
) ] + [
a
1
(-
b
2
) + (-
b
1
)
a
2
]
i
= (
a
1
a
2
-
b
1
b
2
) - (
a
1
b
2
+
b
1
a
2
)
i
. Сондықтан
= (
a
1
-
b
1
i
) ⋅ (
a
2
-
b
2
i
) = [
a
1
a
2
- (-
b
1
) (-
b
2
) ] + [
a
1
(-
b
2
) + (-
b
1
)
a
2
]
i
= (
a
1
a
2
-
b
1
b
2
) - (
a
1
b
2
+
b
1
a
2
)
i
. Сондықтан
 =
=
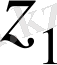 ⋅
⋅
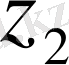 .
.
5.
 = (
a
+
bi
) (
a
-
bi
) =
a
2
- (
bi
)
2
=
a
2
+
b
2
=
= (
a
+
bi
) (
a
-
bi
) =
a
2
- (
bi
)
2
=
a
2
+
b
2
=
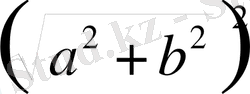 =
z
2
.
=
z
2
.
7.
 = (
a
1
a
2
-
b
1
b
2
) + (
a
1
b
2
+
a
2
b
1
)
i
=
= (
a
1
a
2
-
b
1
b
2
) + (
a
1
b
2
+
a
2
b
1
)
i
=
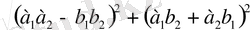 =
=
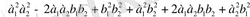 =
=
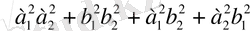 =
=
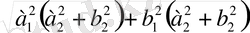 =
=
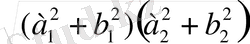 =
=
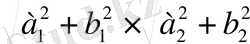 =
=
 .
.
8. Теңсіздікті z 2 = 0 болғанда орындалатынын дәлелдеу керегі де жоқ. Одан әрі z 2 ≠ 0 болсын.
Әуелі z + 1 ≤ z + 1 теңсіздігін дәлелдейік.
5-қасиет бойынша,
z
+ 1
2
= (
z
+ 1) (
 + 1) =
+ 1) =
 2
+
z
+
2
+
z
+
 + 1, ал
z
+
+ 1, ал
z
+
 = 2
a
≤
= 2
a
≤
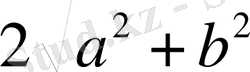 = 2
z
. Сондықтан
z
+ 1
2
≤ (
z
+ 1)
2
. Осыдан
z
+ 1 ≤
z
+ 1.
= 2
z
. Сондықтан
z
+ 1
2
≤ (
z
+ 1)
2
. Осыдан
z
+ 1 ≤
z
+ 1.
Енді z 1 + z 2 = z 2 ( z 1 z 2 -1 + 1) = z 2 z 1 z 2 -1 + 1 . Жаңа ғана дәлелдегеніміз бойынша, z 2 z 1 z 2 -1 + 1 ≤ z 2 ( z 1 z 2 -1 + 1) = z 2 ( z 1 z 2 -1 + 1) = z 1 + z 2 . Сондықтан z 1 + z 2 ≤ z 1 + z 2 .
Комплекс сандардың бөліндісі комплекс сан болады,
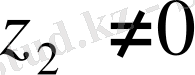
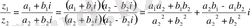
1. 3 Комплекс санның тригонометриялық тұлғасы
Комплекс z = x + yi санының алгебралық тұлғасы деп аталған, мұндағы x , y ∈ R .
Кез келген
z
=
x
+
yi
комплекс саны координаталық жазықтықта
M
(
x
,
y
) нүктесімен немесе
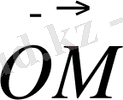 векторымен кескінделеді. Комплекс сандардың және жазықтықтың нүктелері арасындағы сәйкестік өзара бірмәнді болады. Сондықтан комплекс сандарды оларға сәйкес нүктелермен теңестіреді және координаталық жазықтықты
комплекс жазықтық
деп атайды.
векторымен кескінделеді. Комплекс сандардың және жазықтықтың нүктелері арасындағы сәйкестік өзара бірмәнді болады. Сондықтан комплекс сандарды оларға сәйкес нүктелермен теңестіреді және координаталық жазықтықты
комплекс жазықтық
деп атайды.
OX осі нақты ось , OY осі жорамал ось деп аталады.
OM
кесіндінің ұзындығы оған сәйкес
z
санының модуліне тең:
OM
=
z
=
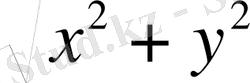 .
.
Енді z = x + yi комплекс саны координаталық жазықтықта M ( x , y ) нүктесімен кескінделсін. Ал ОМ кесіндісі OX осімен жасайтын бұрыш ϕ болсын (оң бағытта, яғни сағат тіліне қарсы бағытта) . Осы ϕ бұрышы z санының аргументі деп аталады және Arg z деп белгіленеді.
Одан әрі
OM
=
z
=
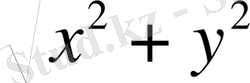 , cos
ϕ
=
, cos
ϕ
=
 , sin
ϕ
=
, sin
ϕ
=
 . Ал cos
ϕ
және sin
ϕ
функциялары периодты және олардың периоды 2
π
болғандықтан Arg
z
=
ϕ
+ 2
πk
,
k
∈
Z
. Әдетте, 0 ≤
ϕ
< 2
π
болса, онда
ϕ
мәні
аргументтің бас мәні
деп аталады және arg
z
деп белгіленеді. Осыдан
z
=
x
+
yi
=
z
cos
ϕ
+
z
sin
ϕ
⋅
i
=
z
(cos
ϕ
+
i
sin
ϕ
) .
. Ал cos
ϕ
және sin
ϕ
функциялары периодты және олардың периоды 2
π
болғандықтан Arg
z
=
ϕ
+ 2
πk
,
k
∈
Z
. Әдетте, 0 ≤
ϕ
< 2
π
болса, онда
ϕ
мәні
аргументтің бас мәні
деп аталады және arg
z
деп белгіленеді. Осыдан
z
=
x
+
yi
=
z
cos
ϕ
+
z
sin
ϕ
⋅
i
=
z
(cos
ϕ
+
i
sin
ϕ
) .
Сөйтіп,
z = z (cos ϕ + i sin ϕ ) . (1)
Бұл z санының тригонометриялық тұлғасы деп аталады. 1- сурет
Түйіндес
z
=
a
+
bi
және
 =
a
-
bi
сандары нақты оське қатысты симметриялық нүктелермен, қарама-қарсы
z
, -
z
нүктелері координаталар басына қатысты симметриялы нүктелермен кескінделеді[2] .
=
a
-
bi
сандары нақты оське қатысты симметриялық нүктелермен, қарама-қарсы
z
, -
z
нүктелері координаталар басына қатысты симметриялы нүктелермен кескінделеді[2] .
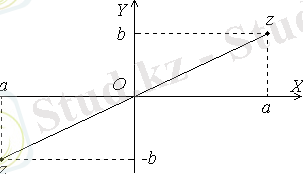
2 - сурет 3 - сурет
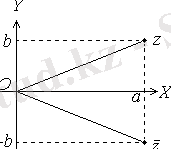
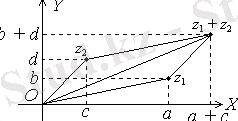
Комплекс
z
1
=
a
+
bi
,
z
2
=
c
+
di
сандары
M
1
(
a
,
b
),
M
2
(
c
,
d
) нүктелерімен кескінделсе, онда
z
1
+
z
2
= (
a
+
c
) + (
b
+
d
)
i
саны
M
3
(
a
+
c
,
b
+
d
) нүктесімен кескінделеді. Бұл
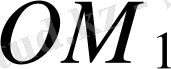 және
және
 векторларын қосқанда,
векторларын қосқанда,
 векторы параллелограмм ережесімен анықталады.
векторы параллелограмм ережесімен анықталады.
4 - сурет
- Комплекс сандарды тригонометриялық тұлғада көбейту және дәрежеге шығару
Теорема Комплекс сандары тригонометриялық тұлғасында берілсін: z = z (cos ϕ + i sin ϕ ), z 1 = z 1 (cos ϕ 1 + i sin ϕ 1 ), z 2 = z 2 (cos ϕ 2 + i sin ϕ 2 ) . Онда
1) z 1 · z 2 = z 1 · z 2 ·[cos ( ϕ 1 + ϕ 2 ) + i sin ( ϕ 1 + ϕ 2 ) ] ;
2)
 =
=
 [cos (
ϕ
1
-
ϕ
2
) +
i
sin (
ϕ
1
-
ϕ
2
) ] ;
[cos (
ϕ
1
-
ϕ
2
) +
i
sin (
ϕ
1
-
ϕ
2
) ] ;
3) z n = z n (cos nϕ + i sin nϕ ), n ∈ N ;
4) (cos ϕ + i sin ϕ ) n = (cos nϕ + i sin nϕ ), n ∈ N (Муавр формуласы) .
Дәлелдеу . 1. z 1 · z 2 = [ z 1 (cos ϕ 1 + i sin ϕ 1 ) ] [ z 2 (cos ϕ 2 + i sin ϕ 2 ) ] = z 1 z 2 (cos ϕ 1 + i sin ϕ 1 ) (cos ϕ 2 + i sin ϕ 2 ) = z 1 z 2 (cos ϕ 1 cos ϕ 2 - sin ϕ 1 sin ϕ 2 ) + i (sin ϕ 1 cos ϕ 2 + cos ϕ 1 sin ϕ 2 ) = z 1 · z 2 ·[cos ( ϕ 1 + ϕ 2 ) + i sin ( ϕ 1 + ϕ 2 ) ] .
2. Енді
z
=
 (cos(-
ϕ
2
) +
i
sin (-
ϕ
2
) ) болсын. Онда 1-формула бойынша,
z
2
·
z
=
z
2
·
(cos(-
ϕ
2
) +
i
sin (-
ϕ
2
) ) болсын. Онда 1-формула бойынша,
z
2
·
z
=
z
2
·
 ·[cos (
ϕ
2
-
ϕ
2
) +
i
sin (
ϕ
2
-
ϕ
2
) ] = 1·(cos 0 +
i
sin 0) = 1. Сондықтан,
z
=
z
2
-1
,
·[cos (
ϕ
2
-
ϕ
2
) +
i
sin (
ϕ
2
-
ϕ
2
) ] = 1·(cos 0 +
i
sin 0) = 1. Сондықтан,
z
=
z
2
-1
,
 =
z
1
·
z
2
-1
= [
z
1
(cos
ϕ
1
+
i
sin
ϕ
1
) ] [
=
z
1
·
z
2
-1
= [
z
1
(cos
ϕ
1
+
i
sin
ϕ
1
) ] [
 (cos(-
ϕ
2
) +
i
sin (-
ϕ
2
) ] . Осыдан 1-формула бойынша,
(cos(-
ϕ
2
) +
i
sin (-
ϕ
2
) ] . Осыдан 1-формула бойынша,
 =
z
1
=
z
1
 [cos (
ϕ
1
-
ϕ
2
) +
i
sin (
ϕ
1
-
ϕ
2
) ] =
[cos (
ϕ
1
-
ϕ
2
) +
i
sin (
ϕ
1
-
ϕ
2
) ] =
 [cos(
ϕ
1
-
ϕ
2
) +
i
sin(
ϕ
1
-
ϕ
2
) ] .
[cos(
ϕ
1
-
ϕ
2
) +
i
sin(
ϕ
1
-
ϕ
2
) ] .
3. n = 1 үшін формула орындалады. Енді формула n ≥ 1 үшін орындалсын. Онда z n +1 = z n · z = [ z n (cos nϕ + i sin nϕ ) ] [ z (cos ϕ + i sin ϕ ) ] . Осыдан 1-формула бойынша, z n +1 = z n z [cos( nϕ + ϕ ) + i sin( nϕ + ϕ ) ] = z n +1 [cos( n + 1) ϕ + i sin( n + 1) ϕ ] .
Математикалық индукция принципі бойынша, кез келген натурал n үшін z n = z n (cos nϕ + i sin nϕ ) .
4. Бұл 3-қасиеттің z = 1 жағдайы.
1. 5 Комплекс санның көрсеткіштік тұлғасы
(cos ϕ + i sin ϕ ) = e iφ Эйлер формуласынан, комплекс санның көрсеткіштік тұлғасы шығады: z = a+bi= z (cos ϕ + i sin ϕ ) =z e iφ
- Бірдің түбірлері
Анықтама 1 . 6. 1 Натурал n саны үшін z n = 1 болатын z комплекс саны бірдің n - дәрежелі түбірі деп аталады.
Бірдің n -дәрежелі түбірлерінің жиыны U n деп белгіленеді.
Теорема 1 . 6. 1. Бірдің n дәрежелі барлық түбірлерінің саны дәл n -ге тең болады және олар
ε
k
= cos
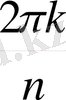 +
i
sin
+
i
sin
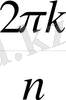 ,
k
= 0, 1, …,
n
- 1, (1)
,
k
= 0, 1, …,
n
- 1, (1)
формуласымен беріледі.
Дәлелдеу
:
ε
k
n
= (cos
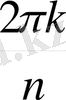 +
i
sin
+
i
sin
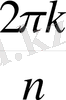 )
n
= cos
)
n
= cos
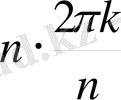 +
i
sin
+
i
sin
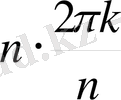 = cos(2
πk
) +
i
sin(2
πk
) = 1, яғни, барлық
ε
k
бірдің түбір болады. Ал
= cos(2
πk
) +
i
sin(2
πk
) = 1, яғни, барлық
ε
k
бірдің түбір болады. Ал
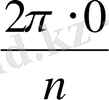 ,
,
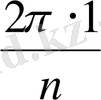 , …,
, …,
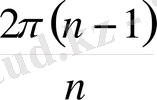 сандары 2π-ден кем теріс емес әр түрлі сандар. Осы бұрыштарға әртүрлі комплекс сандар сәйкес келеді. Сондықтан
i
≠
j
болса,
ε
I
≠
ε
j
. Енді
ε
k
-лардан басқа бірдің түбірі жоқ екенін дәлелдейік.
сандары 2π-ден кем теріс емес әр түрлі сандар. Осы бұрыштарға әртүрлі комплекс сандар сәйкес келеді. Сондықтан
i
≠
j
болса,
ε
I
≠
ε
j
. Енді
ε
k
-лардан басқа бірдің түбірі жоқ екенін дәлелдейік.
Шынында,
z
=
z
(cos
ϕ
+
i
sin
ϕ
) саны бірдің
n
-дәрежелі түбірі болсын:
z
n
=
z
n
(cos
nϕ
+
i
sin
nϕ
) = 1. Осыдан
z
n
(cos
nϕ
+
i
sin
nϕ
) = 1,
z
n
cos
nϕ
= 1,
z
n
sin
nϕ
= 0. Сондықтан
z
= 1,
nϕ
= 2
π
·
m
,
m
∈
Z
. Енді
m
санын
n
ға қалдықпен бөліп,
m
=
nq
+
k
, 0 ≤
k
<
n
, түрінде жазамыз. Осыдан
z
= cos
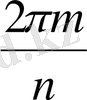 +
i
sin
+
i
sin
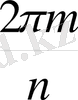 = cos
= cos
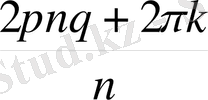 +
i
sin
+
i
sin
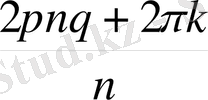 = cos
= cos
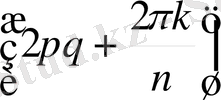 +
i
sin
+
i
sin
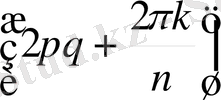 = cos
= cos
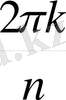 +
i
sin
+
i
sin
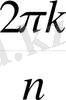 =
ε
k
, 0 ≤
k
<
n
. Сондықтан
z
=
ε
k
.
=
ε
k
, 0 ≤
k
<
n
. Сондықтан
z
=
ε
k
.

5 - сурет
Салдар . Бірдің n -дәрежелі түбірлеріне сәйкес нүктелер комплекс жазықтықта центрі координаталар басында жататын бірлік шеңберге іштей сызылған дұрыс көпбұрыштың төбелерінде жатады.
n = 6 жағдайы жоғарғы суретте көрсетілген.
Теорема 1 . 6. 2. Бірдің n -дәрежелі түбірлерінің U n жиыны көбейту операциясына қатысты коммутативтік топ құрайды.
Дәлелдеу . Егер u және v бірдің n -дәрежелі түбірі болса, онда u n = 1 және v n = 1. Осыдан ( uv ) n = u n v n = 1. Сондықтан бірдің n -дәрежелі түбірлерінің көбейтіндісі де бірдің n -дәрежелі түбірі болады. Ал 1 n = 1. Сондықтан бірдің түбірлер жиынында 1 саны да болады. Ол көбейтуге қатысты бейтарап элемент.
Егер u бірдің түбірі болса, онда u n = 1. Осыдан u · u n -1 = 1. Сондықтан u -ға кері элемент u n -1 саны болады. Ол да бірдің түбірі болады: ( u n -1 ) n = ( u n ) n -1 = 1.
Сөйтіп, бірдің n -дәрежелі түбірлерінің жиыны топ құрайды. Ал өрісте көбейту коммутативтік болады. Сондықтан бірдің n -дәрежелі түбірлерінің U n жиыны коммутативтік топ құрайды.
Анықтама 1 . 6. 2 Егер бірдің n -дәрежелі n -нан кем оң дәрежелі түбір болмаса, онда ол бірдің n -дәрежелі алғашқы түбірі деп аталады.
Басқа сөзбен айтқанда, комплекс z саны n -дәрежелі бірдің алғашқы түбірі болады, егер z n = 1 және кез келген k , 0 < k < n , саны үшін z k ≠ 1 болса.
Теорема 1 . 6. 3 1°. Комплекс z саны бірдің n -дәрежелі алғашқы түбірі болады, сонда тек сонда ғана 1, z , z 2 , …, z n -1 сандары әртүрлі болады.
2°. Егер комплекс z саны бірдің n -дәрежелі алғашқы түбірі болса, онда z k саны бірдің n -дәрежелі алғашқы түбірі болады, сонда тек сонда ғана k мен n сандары өзара жай болады.
3°. Бірдің n -дәрежелі алғашқы түбірлерінің саны ϕ ( n ) болады, мұндағы ϕ ( n ) Эйлер функциясы, яғни n -нан кем және n -мен өзара жай сандардың саны.
Дәлелдеу . Комплекс z саны бірдің n -дәрежелі алғашқы түбірі және z i = z j , n > i ≥ j , болсын. Онда z i - j = 1 және 0 ≤ i - j < n . Сондықтан i - j = 0 немесе i = j , өйткені z санының n -нан кем оң дәрежесі 1-ге тең бола алмайды. Осыдан 1, z , z 2 , …, z n -1 дәрежелері әртүрлі болады.
Егер 1, z , z 2 , …, z n -1 дәрежелері әртүрлі болса, онда z саны бірдің n -нан кем оң дәрежелі түбір болмайды.
2°. Комплекс z саны бірдің n -дәрежелі түбірі, 0 < k < n және d = ( n , k ) болсын. Онда n = n 1 d , k = k 1 d , мұндағы ( n 1 , k 1 ) = 1.
Егер
z
k
саны бірдің
n
-дәрежелі алғашқы түбірі болса, онда
 =
=
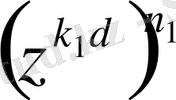 =
=
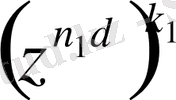 =
=
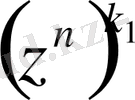 = 1. Сондықтан
z
k
саны бірдің
n
1
-дәрежелі түбірі болады. Ал
z
k
алғашқы түбір, сондықтан
n
1
=
n
. Осыдан
d
= 1 және
n
мен
k
өзара жай болады.
= 1. Сондықтан
z
k
саны бірдің
n
1
-дәрежелі түбірі болады. Ал
z
k
алғашқы түбір, сондықтан
n
1
=
n
. Осыдан
d
= 1 және
n
мен
k
өзара жай болады.
Енді
n
мен
k
өзара жай және (
z
k
)
m
= 1, 0 <
m
≤
n
болсын. Онда
z
km
= 1 болғандықтан,
km
 n
болу керек. Ал
k
мен
n
өзара жай, сондықтан
m
n
болу керек. Ал
k
мен
n
өзара жай, сондықтан
m
 n
. Онда
m
=
n
болу керек, өйткені
m
≤
n
. Сондықтан
z
k
санының 1-ге тең болатын ең кіші оң дәрежесі (
z
k
)
n
болады. Сөйтіп,
z
k
саны бірдің
n
-дәрежелі алғашқы түбірі болады.
n
. Онда
m
=
n
болу керек, өйткені
m
≤
n
. Сондықтан
z
k
санының 1-ге тең болатын ең кіші оң дәрежесі (
z
k
)
n
болады. Сөйтіп,
z
k
саны бірдің
n
-дәрежелі алғашқы түбірі болады.
3°. Бұл 2-қасиеттен және Эйлер функциясының анықтамасынан шығады.
Жоғары табылған бірдің 3-дәрежелі
ε
0
= 1,
ε
1
= -
 +
i
+
i
 ,
ε
2
= -
,
ε
2
= -
 -
i
-
i
 түбірлерінің арасында алғашқы түбір
ε
1
және
ε
2
болады.
түбірлерінің арасында алғашқы түбір
ε
1
және
ε
2
болады.
Бірдің 8-дәрежелі алғашқы түбірлері
ε
1
=
 +
i
+
i
 ,
ε
3
= -
,
ε
3
= -
 +
i
+
i
 ,
ε
5
= -
,
ε
5
= -
 -
i
-
i
 ,
ε
7
=
,
ε
7
=
 -
i
-
i
 сандары болады [3] .
сандары болады [3] .
1. 7 Кез келген комплекс санның түбірлері
Анықтама . Комплекс z саны үшін u n = z болатын u саны z санының n-дәрежелі түбірі деп аталады.
Теорема 1. 7. 1 Нөлден өзге комплекс z санының n -дәрежелі түбірлерінің саны дәл n болады. Егер ол сан z = z (cos ϕ + i sin ϕ ) тригонометриялық тұлғасында болса, онда z санының n -дәрежелі түбірлері келесі формуламен анықталады:
z
k
=
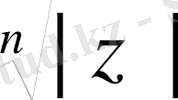 (cos
(cos
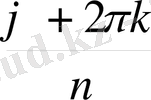 +
i
sin
+
i
sin
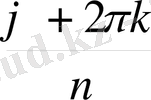 ,
k
= 0, 1, …,
n
- 1. (2)
,
k
= 0, 1, …,
n
- 1. (2)
Дәлелдеу
. 4-Теорема бойынша,
z
k
n
=
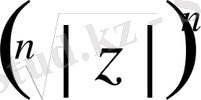 [cos
[cos
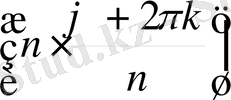 +
i
sin
+
i
sin
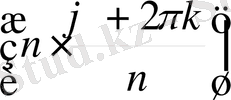 ] =
z
[cos(
ϕ
+ 2
πk
) +
i
sin(
ϕ
+ 2
πk
) ] =
z
. Сондықтан барлық
z
k
сандар
z
санының
n
дәрежелі түбірлері болады және
i
≠
j
болса, онда
z
i
≠
z
j
. Енді осылардан басқа түбір жоқ екенін дәлелдейміз. Айталық,
u
=
u
(cos
ψ
+
i
sin
ψ
) үшін
u
n
=
z
болсын. Онда
u
n
=
u
n
(cos
nψ
+
i
sin
nψ
) =
z
(cos
ϕ
+
i
sin
ϕ
) . Осыдан
u
n
=
z
, яғни
u
=
] =
z
[cos(
ϕ
+ 2
πk
) +
i
sin(
ϕ
+ 2
πk
) ] =
z
. Сондықтан барлық
z
k
сандар
z
санының
n
дәрежелі түбірлері болады және
i
≠
j
болса, онда
z
i
≠
z
j
. Енді осылардан басқа түбір жоқ екенін дәлелдейміз. Айталық,
u
=
u
(cos
ψ
+
i
sin
ψ
) үшін
u
n
=
z
болсын. Онда
u
n
=
u
n
(cos
nψ
+
i
sin
nψ
) =
z
(cos
ϕ
+
i
sin
ϕ
) . Осыдан
u
n
=
z
, яғни
u
=
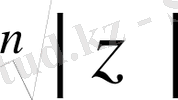 ,
nψ
=
ϕ
+ 2
πm
. Енді
m
санын
n
-ға қалдықпен бөлейік:
m
=
nq
+
k
, 0 ≤
k
<
n
. Осыдан
u
=
,
nψ
=
ϕ
+ 2
πm
. Енді
m
санын
n
-ға қалдықпен бөлейік:
m
=
nq
+
k
, 0 ≤
k
<
n
. Осыдан
u
=
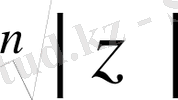 (cos
(cos
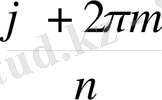 +
i
sin
+
i
sin
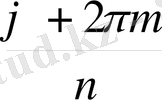 ) =
) =
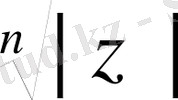 (cos
(cos
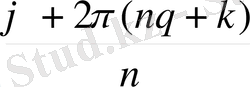 +
i
sin
+
i
sin
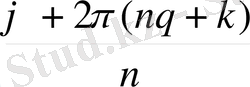 ) =
) =
 (cos
(cos
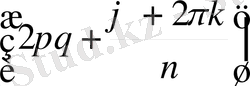 +
i
sin
+
i
sin
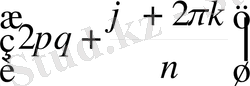 ) =
) =
 (cos
(cos
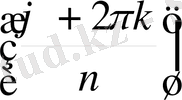 +
i
sin
+
i
sin
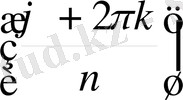 ) =
z
k
. Сөйтіп,
u
=
z
k
.
) =
z
k
. Сөйтіп,
u
=
z
k
.
Теорема 1. 7. 2 Комплекс u саны z санының n -дәрежелі түбірі және ε бірдің n -дәрежелі алғашқы түбірі болсын. Онда z санының барлық n -дәрежелі түбірлері u , uε , uε 2 , . . . , uε n -1 сандары болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz