Модуль белгісімен берілген анықталмаған теңсіздіктер жүйесі

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

Мазмұны

Кіріспе
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ...3

1 Нақты санның модулі және оның қасиеттері
... ... ... ... ... ... ... ... ... ... ... ... ... ... .5

1.1 Нақты санның
модулі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... . 5
1.2 Нақты санның модулінің
қасиеттері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
..6

2 Теңсіздік және теңдік теңдеулерінің түсініктері
... ... ... ... ... ... ... ... ... ... ... ... ...9

3 Модуль белгісімен берілген анықталмаған теңдеулер
... ... ... ... ... ... ... ... ... ...14

4 Модульмен берілген теңдеулер жүйесі
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 18

5 Модуль белгісімен берілген анықталмаған теңсіздіктер жүйесі
... ... ... ... ... ..50

5.1 Модульмен берілген қарапайым теңсіздіктер
... ... ... ... ... ... ... ... ... ... ... ... ..55
5.2 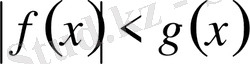түріндегі теңсіздіктер
... ... ... ... ... ... ... ... ... ... ... ... . ... ... ... ... ... .57
5.3 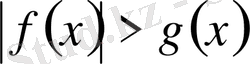түріндегі
теңсіздік
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
58 5.4
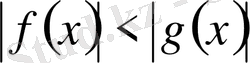түріндегі теңсіздік
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
61

6 Өздігінен шығаруға арналған есептер
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..72

Қорытынды
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... .76

Пайдаланған әдебиеттер тізімі
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... 77

Кіріспе

Модуль түсінігі нақты сандар облысында да, комплексті сандар облысында
да санның маңызды сипаттамаларының бірі болып табылады. Модуль сөзі латын
тілінің modulus- өлшем деген сөзінен шыққан. Бұл терминді алғаш ағылшын
математигі Р. Котес (1682 – 1716), ал модуль белгісін К.Вейерштрасс (1815 –
1897) в1841ж. енгізді [1].
Тақырыптың өзектілігі: Модуль түсінігі мектептегі математика курсының әр
түрлі бөлімдерінде ғана емес ЖОО- нда оқылатын жоғарғы математика курсында,
физикада және техникалық ғылымдарда кеңінен қолданылады. Мысалы: жуықталған
есептеулер теориясында жақындатылған санның абсолютті және қатыстың
қателіктер түсінігі қолданылады. Механика және геометрияда вектор және оның
ұзындығы (вектор модулі) түсініктері оқылады. Математикалық талдауда санның
абсолютті ұзындығы түсінігі шек, шектік функция және т. б. негізгі
түсініктердің анықтамаларының құрамына кіреді. Абсолютті ұзындықпен
байланысты есептер математикалық олимпиадаларда, ҰБТ- да жиі кездеседі.
Практика көрсеткендей, модуль түріндегі тапсырмалар оқушылар мен
талапкерлерге жеткілікті түрде қиын, бұл обективті қиындық мынамен
түсіндіріледі, яғни мектептегі математика курсы оқушылардың берік білім-
білік дағдыларын қалыптастыруға жеткілікті дәрежеде қамтамасыз ете
алмағандығында. Осындай проблемалық жағдайларды ескере отырып берілген
дипломдық жұмыста модуль белгісімен берілген теңдеулер, теңсіздіктер,
теңдеулер мен теңсіздіктер жүйесі түріндегі есептердің аналитикалық,
геометриялық шығару жолдары жүйелеп қарастырылған. Теориялық жағынан
қарастыратын болсақ, модульдің анықтамасы, қасиеттері, сүлбе нұсқалары
көрсетілген. Оқушылар осы материалдарға сүйене отырып, кез келген модульмен
берілген есептерді теориялық және практиктикалық тұрғыда жан жақты
қолдануға мүмкіндікері зор.

Дипломдық жұмыстың мақсаты: Модульдер туралы теориялық білімдерін
жүйелеу және оның қасиеттерін қолдана отырып, есептердің шығару жолдарын
анықтау.

Зерттеу обьектісі: Мектеп үрдісінде модульмен берілген әр түрлі есептер.

Дипломдық жұмыстың міндеттері:

1.Модульдермен берілген есептерге талдау жасау;

2.Модульдермен берілген әр түрлі есептерді шешу әдістерін қарастыру;

3.Берілген тақырыпқа қатысты теңдеулер мен теңсіздіктер жүйесін
қарастыру.

Дипломдық жұмыс алты бөлімнен тұрады:

Бірінші бөлімде модульдің анықтамалары, оның геометриялық
интерпретациясы, абсолютті шама қасиеттері келтірілген. Модульді қолданып,
анықталу облысы бірдей теңдік пен теңсіздіктің кез келген жүйесін бір
салыстыру түрінде алуға болатыны мысал арқылы көрсетілген. Модуль қасиеті,
теңдік немесе абсолютті шаманың белгісіне ие теңдікке мысал ретінде есептеу
келтірілген.

Екінші бөлімде модульмен берілген теңдеулер жүйесін шешу тәсілдері
келтірілген. Онда шығатын жүйені түрлендіріп, оның шешімдерін табамыз.

Үшінші бөлімде модулі белгісіз болатын теңдеулерді қарастыру. Оларды
шешудің әртүрлі әдістерін.

Төртінші бөлімде абсолюттік шаманың белгісі бар теңдіктер мен
теңсіздіктерді графикалық жолмен шешу тәсілдері келтірілген модульдермен
берілген теңдеулер мен теңсіздіктерді графикалық шешу кейбір жағдайларда
аналитикалық шешіміне қарағанда қолайлырақ болады. Бұл бөлімінд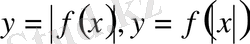е және
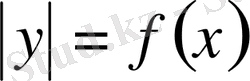функцияларының графиктерін салу қарастырылған.

Бесінші бөлімде модульдерге қолданылатын теңсіздіктер түрлері.

1)Модулдері бар қарапайым теңсіздіктер, модульдері бар теңсіздіктер
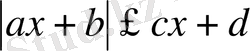және 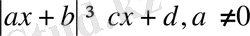түріндегі теңсіздіктер болып табылады.

2) 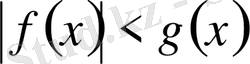түріндегі теңсіздіктер,

3) 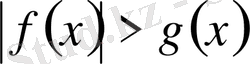түріндегі теңсіздіктер,

4) 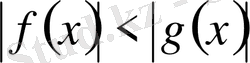түріндегі теңсіздіктерді шеше білу.

Алтыншы бөлімде абсолютті шаманың түсінігімен байланысты есептерді шешу
мысалдары келтірілген. стандартты есептердің шешімімен қатар, параметрі
бар есептердің де шешімдері келтірілген Олардың шешімінде қандай да бір
шешімдердің комбинациясын алу керек. Кейбір есептер үшін бірнеше шешу
әдістері келтірілген, кейде шешу процесінде туындайтын қателіктер
көрсетіледі. Барлық есептер үшін жылдамдығы бойынша ең тиімді шешімдер
көрсетілген .

1. Нақты санның модулі және оның қасиеттері

1. Нақты санның модулі

Анықтама. Егер х-саны теріс емес болса, онда оның өзі аталады.

Егер теріс болса х- санына қарама-қарсы сан кесінді ұзындығы аталады
[2]. Қысқаша:

Нақты санның модулінің геометриялық мағынасын қарастырайық.

Бұл сан координатасы болып табылатын , әрбір нақты санға сандық түзуден
нүкте сәйкес келеді. Бұл санның модулі – осы сандық осьтегі сәйкес нүктеден
координата басына дейінгі қашықтық (1.1.1-сурет). А нүктесінен О нүктесіне
дейінгі қашықтық тең.

А О В

-a 0
a

1.1.1- сурет

a,b сандарының модульдерінің айырымы , a және b
нүктелерінің ара қашықтығына сәйкес (1.1.2-сурет).

а о
b

1.1.2-
сурет

1.2 Нақты санның модулінің қасиеттері

1) Модульдің квадраты модуль ішіндегі өрнектің квадратына тең, яғни
кез келген үшін .

Ескерту. Бұл формула тек солдан оңға ғана емес, яғни , оңнан
солға да: қолданылады.

2) Кез келген нақты санның модулінде теріс сан бар, яғни
барлық үшін .

3) Нақты санның модулі осы саннан кем емес, яғни барлық үшін
.

4) нақты санының модулі, және екі қарама-қарсы санның
максимумна тең, яғни .

5) Олардың қосындысы осы сандардың модульдерінің қосындысына тең
болғанда, сонда тек сонда ғана сандар теріс емес, яғни қосындысы
жүйесіне пара-пар.

6) Олардың модульдерінің қосындысы осы сандардың қосындысына қарама-
қайшы болғанда, сонда тек сонда ғана сандар оң емес, яғни

теңдігі жүйесіне пара-пар.

7) Олардың модульдерінің қосындысы олардың қосындысының модуліне тең
болғанда,сонда тек сонда ғана сандар бір уақытта теріс емес және оң да
емес, яғни теңдігі немесе екі теңдеулер жүйесіне пара-
пар.

8) Екі санның модульдерін салыстыру олардың квадраттарының
салыстыруына пара-пар,яғни келесідей пара-парлық орын алады:

пара-пар

пара-пар

пара-пар

пара-пар

пара-пар

9) Екі нақты санның көбейтіндісінің модулі көбейткіш модулінің
көбейтіндісіне тең, яғни .

10) Бөлімі нөлден өзгеше бөлшектің модулі, жеке бөлінген алымы мен
бөлімінің модульдарына тең, яғни 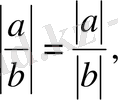мұндағы b

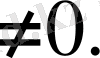
11) Кез келген бүтін мәні үшін .

12) Егер - жұп сан болса, онда .

13) Түбір астындағы квадраттық сан осы санның модуліне тең: .

14) Екі нақты санның айырымының модулі олардың модульдерінің айырымынан
кіші емес .

15) Екі нақты санның қосындысының модулі олардың модульдерінің
айырымынан кіші емес .

16) Кез келген және нақты сандары үшін қос теңсіздік орын
алады:

17) Кез келген және нақты сандары үшін теңсіздігі әділ:

18) Кез келген және нақты сандары үшін теңдігі әділ:

19) Кез келген нақты сандардың қосындысының модулі олардың модульдерінің
қосындысынан аспайды, яғни

.

20) Екі нақты сандардың қосындысы теріс емес, ал олардың көбейтіндісі
оң, сонда тек сонда ғана модульдерінің айырымының модулі осы сандардың
қосындысына тең, яғни теңдігі

22) теңдеуі теңсіздігіне пара-пар.

23) теңдеуі , егер қос теңсіздігіне пара-пар [3].

2 Теңсіздік және теңдік теңдеулерінің түсініктері

Анықтама 1. Егер (1)-ші теңдеудің шешімі (2)-ші теңдеудің болса, онда
(2)-ші теңдеу (1)-ші теңдеудің салдары деп аталады.

Қысқаша былай жазылады: 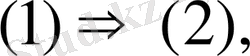мұндағы -логикалық бағыт белгісі.

-жазылудың оқылуы: (1) теңдеуінен (2) теңдеу шығады

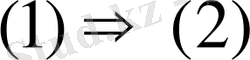
Анықтама 2. Егер (1)-ші теңдеу (2)-ші теңдеуінің саладары болса,
керісінше, (2)-ші теңдеу (1)-ші теңдеудің салдары бола алса, немесе екі
тендеу де шешімдері болмаса, онда екі теңдеудің (1) және (2) бірдей
белгісізі бар тепе-тең (эквиваленті) теңдеу деп аталады.

Теңдеулердің тепе-теңдігі қысқаша былай жазылады: (1)(2), мұндағы
-логикалық тепе-теңдіктің (эквиваленттің) белгісі.

Басқаша айтқанда, белгісіз екі теңдеу бір-біріне қатысты тепе-тең , егер
шешімдерінің көбі сәйкес келсе.

Теңдеулердің тепе-тең түрлендіруі туралы теоремның қалыптастыруына
келмей тұрып, тепе-тең бірдей өрнектердің және тепе-тең өзгертудің
маңызды түсініктерін қарастырайық.

Анықтама 3. Егер мүмкін мәндер облыстары оларға сәйкес келсе және мүмкін
мәндердің облысынан алынған барлық әріптердің мағыналарына өрнектердің
сандық мағыналары тең болса, тепе-тең бірдей екі өрнек деп аталады.

Анықтама 4. Басқа өзгертумен тепе-тең бір өрнектің ауыстыруы аталады ,
оған тепе-тең бірдеймен .

Мысал қарастырайық. 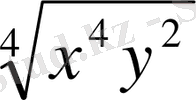(1) өрнегі 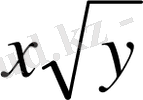(2) өрегімен ауыстырылсын.
(1) өрегінде мүмкін мәндердің обылысы (ММО) 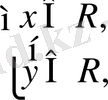жүйе түрінде беріледі, ал
(2)-ші өрнекте ММО 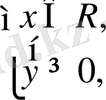жүйе түрінде беріледі. (1) және (2) өрнегтерінің
ММО сәйкес келмегендіктен, (1) және (2) өрнегі тепе-тең емес.

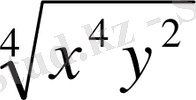өрнегін 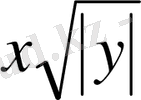(3) өрнегімен ауыстырайық. Мына (1) және (3) екі
өрнегінің ММО сәйкес келеді, себебі (3) өрнегінің ММО жүйесі 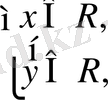түрінде
беріледі, яғни (1) өрнектің ММО-дай болғандықтан.

Бірақ ММО-лары бірдей болғанымен, (1) және (3) өрнектері тепе-тең емес.
Расыменде, мысалы ММО-на жататын 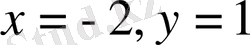деп алсақ, біз (1)-ші өрнегтің
сандық мәні 2 тең, ал (3) өрнектің сандық мәні – (-2) тең болады. Демек,
ММО-на жататын (1) және (3) өрнектерінің сандық мәнідері әріптердің
кекелген мағыналарында емес.

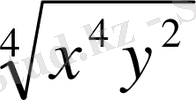өрнегін 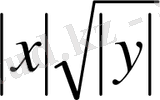(4) өрнекпен ауыстырайық. (1) және (4) өрнегі тепе-тең
(оқырманға мына бекіту негіздеуін пайдалануына береміз). Теңдеуледің
(теңсіздіктердің) тепе-теңдігі келесі теоремалардың арқасында орынадалады.

Теорема 1. Егер осы теңдеуді алмастырғанда, облыстар аймағы ауыспайтын
тап осы екі теңдеудің бөліктеріне тепе-тең өзгертулер енгізсек , онда тап
осыған тепе-тең теңдеуді аламыз.

Теорема 2. Егер дәл осы берілген теңдеудің екі бөлігіне де дәл сол санды
немесе дәл сол өрнекті қоссақ, берілген теңдеудің анықталу обылысындағы
барлық белгісіздерде мағнасына бар, тап осыған тепе-тең тендеу аламыз.

Салдары. Теңдеудің мүшелерін таңбаларын қарама-қарсы таңбаға ауыстыра
отырып, бір бөліктен басқа бөлікке ауыстыруға болады.

Теорема 3. Егер берілген теңдеудің екі бөлігінде дәл осы санға, нөлге
тең емес, немесе дәл осы өрнекке көбейтсе, берілген теңдеудің анықталу
обылысындағы барлық белгісіздерде мағнасы бар және нөлге тең емес болса,
онда тап осыған тепе-тең теңдеуді аламыз.

Салдар 1. Егер теңдеудіуің мүшелерінің арасында бөлшек сандар кездессе,
онда теңдеудің олардан екі бөлігінде ең кіші жалпы еселі бөлшек
мүшелердің бөлгіштерін көбейтуімен құтылуға болады, және де алынған
теңдеу, ең кіші жалпы еселі нөльге тең емес, белгісіздің барлық
мағыналарында тап осыған тепе-тең.

Салдар 2. Егер берілген теңдеудің анықталу обылысындағы барлық
белгісіздерде мағнасы бар және нөлге тең емес, барлық мүшелері бірдей санға
немесе өрнекке бөлінсе, онда оларды осы санға немесе өрнекке бөлуге болады.

Теорема 4. Егер (1) теңдеуі (2) теңдеуіне тепе-тең болса, ал (2) теңдеуі
(3) теңдеуіне тепе-тең болса, онда (1) теңдеуі (3) теңдеуіне тепе-тең.

Егер берілген теңдеудің шешімі 1,2,3,4, теоремалары арқылы өткізілсе,
онда табылған түбірдің тексерілуі қажет емес. Егер де осы теоремалар
шартына кірмейтін басқа да бір өзгертулер қолданылса, онда табылған
белгізідің берілген теңдеудің шартына сәйкес тексерілуі керек, яғни
теңдеудің шешімінің құрамдас бөлігі болады [4].

Соңғы ескерту иррационалдық, көрсеткіш, логарифмдік, көрсеткіш дәреже,
көрсеткіш-логарифмдік және тригонометриялық теңдеулерге ерекеше қатысты.

Тепе-тең теңсіздіктерге (теңдеулерге) келтірілетін негізгі операцияларды
көрсетейік.

1. Егер Х жиында анықталған функциялары, онда Х-қа

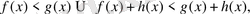
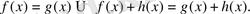
2. Егер Х-та 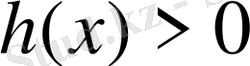, онда Х-қа

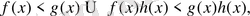
яғни теңсіздіктерді оң функция көбейткенде, теңсідіктің таңбасы
өзгермейді.

3. Егер Х-та 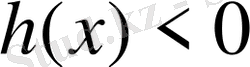, онда Х-қа

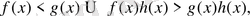
яғни теңсіздіктерді теріс функцияға көбейткенде, теңсідіктің таңбасы
қарама-қарсы өзгереді.

4. Егер Х-та , онда Х-қа

яғни теңсідіктің немесе теңдеудің екі жағыда теріс емес болса, онда
теңсіздіктің немесе теңдеудің екі жағында квадртқа (немесе кез-келген жұп
дәрежеге) келтіру сәйкесінше теңсіздіктің немесе теңдеудің тепе-теңдігіне
әкеледі.

Егер теңсідіктің сол немесе оң жақ бөліктерінде әр түрлі таңбалары
болса, онда теңсідікті квадраттауға болмайды, өйткені квадраттаған кезде
теңсіздік тепе-тең де, тепе-тең емес те түрге келуі мүмкін: -45 және
1625; -75, бірақ 4925.

Егер де және әр түрлі таңбалармен болса, онда
мынатеңдеуден теңдеуі шығады, бірақ ол берілгенге тепе-тең емес,
өйткені тағыда теңдеудің шешімін құрайды. Сол себептен жұп дәрежеге
алғанда, жиі квадратқа алғанда, бөтен түбірлер пайда болуы мүмкін.

Модуль белгісімен берілген анықталмаған тепе-тең теңсіздіктерге тағы да
теоремалар келтірейік.

1. теңдеуі жүйелердің жиынтығына тепе-тең

2. Теңдеңдеуді модульсіз теңдеуге ауыстырудың екі түрлі әдісі
бар.

а) Бұл теңдеу жүйелердің жиынтығына тепе-тең

б) Бұл теңдеу жүйелердің жиынтығына тепе-тең

Егер теңдеуде функциясы функциясына қарағанда қарапайым
түрде болса, онда бұл теңдеу бірінші жүйелердің жиынтығын мақсатқа лайықты
түрде ауыстырады, ал егер функциясы қарапайым түрде болса, онда бұл
теңдеу екінші жүйелердің жиынтығын мақсатқа лайықты түрде ауыстырады.

3. түріндегі теңдеу, мұндағы жүйенің жиынтықтарын тепе-тең кейбір
функциялар.

4. түріндегі теңдеуді қарастырайық,

мұндағы кейбір функциялар. Мұндай теңдеулердің шешімдері келесідей
құралады. функциясынан кем дегенде біреуінің таңбасының мәні ауыстын
барлық нүктелерді табады. Бұл нүктелер әрбір барлық функциялар
таңбаларын сақтап, негізгі теңдеудің анықталу облысын аралықтарға бөледі.
Содан кейін, модульдің анықтамасын қолдана отыра, модуль таңбасы болмайтын
негізгі теңдеуден жүйенің жиынтығына көшеді.

Модуль астында анықталмаған теңсіздіктер мен теңдеулерді шешкенде,
келесі әдістер негізгі болып табылады: анықтама бойынша модульдің ашылуы;
теңдеудің (теңсіздіктің) екі жағында квадратқа алғанда; теңдеудің
(теңсіздіктің) анықталу обылысын аралықтарға бөлу әдісі; модуль астындағы
өрнектер өз таңбасын сақтап қалғанда; графикалық әдіс.

Бұл жұмыста оқырман тепе-теңдікке әкелетін теңсіздіктер туралы
толығырақ мәлеметтер ала алады ( жұмыста 38 бекіту қарастырылған) [5].

3 Модуль белгісімен берілген анықталмаған теңдеулер

Модуль астындағы белгісімен берілген анықталмаған теңдеудің шешуін
қарастырайық.

1) теңдеудің түрі. Берілген теңдеу теңсідігіне тепе-тең.

Тапсырма3.1. Теңдеуді шешіңдер

Шешуі:

Берілген теңдеу теңсідігіне тепе-тең, мұндағы

Жауабы:

Тапсырма3.2. Теңдеуді шешіңдер

Шешуі

Берілген теңдеуді түрінде жазамыз. Бұл теңдеу теңсідігіне тепе-
тең, мұндағы

Жауабы:

2. теңдеудің түрі.

Мұндай теңдеулерді екі түрлі әдіспен шығаруға болады.

Бірінші әдіс- функциясы -нан қарапайым болса қолданылады.

Егер болғанда, теңдігі орындалады және теңдеуі түріне
келеді;егер болғанда, теңдігі орындалады және теңдеуі
түріне келеді.

Және, керісінше, егер және , онда , ал егер және
, онда тағыда немесе

Мұнда теңсіздікті шешу қажет емес, тек қана шықан шешімді сәйкес
тендеуге қою керек. Басқашада істеуге болады: теңдеудің жиынтығын шешіп
содан кейін жай ғана тексеруге болады.

Тағыда, берілген теңдеуді жүйеге тепе-тең деп айтуға болады

Тапсырма 3.3. Теңдеуді шешіңдер

Шешуі:

Біз мынадай жауап аламыз:

Жауабы:

Тапсырма 3.4. Теңдеуді шешіңдер

Шешуі:

Берілген теңдеу келесі жүйеге тепе-тең:

Бұл берілген жүйенің бірінші теңдеуін шешейік:

болғанда екінші теңсіздік орындалмайды. болғанда екінші
теңсіздік орындалады.

болсын. Үшінші жүйенің шартын тексерейік:

яғни болғанда жүйенің шешімі бола алмайды. болғанда
аналогиялық түрде істейміз:

яғни болғанда жүйенің шешімі бола алады.

Жауабы: .

Тапсырма 3.5. Теңдеуді шешіңдер

Шешуі:

Шығарылып жатқан теңдеудің анықталу обылысын көрсетейік. Ол жүйе түрінде
беріледі

мұндағы, жүйенің бірінші теңсіздігінің сол жақ бөлігін көбейткіштерге
жіктесек,

аламыз.

Жүйеге кіретін, теңдеудің квадрат түбірін тапсақ,

аламыз.

Шығарылып жатқан теңдеуді мына түрде жазайық

бұдан

Шығарылып жатқан теңдеудің анықталу обылысы соңғы теңдеудің жиынтығына
тепе-тең

бұдан

Жиынтықтың теңдеуін шешіп, Теңдеудің анықталу обылысында
түбірі бөгде.

Жауабы:

4 Модульмен берілген теңдеулер жүйесі

Модульмен берілген теңдеулер жүйесін, модульмен берілген теңдеулерді
шешу тәсілдері сияқты шығарылады. Есепті шешудің негізгі әдістері
алгебралық және геометриялық әдіс болып табылады [6].

Мысалдардың кейбір түрлерін қарастырайық.

Тапсырма 4.1.1 - ге қатынасты табыңыз, егер жүйесінің шешімі
болатындай мәнін табыңыз.

Шешуі:

Екінші теңдеуден - ті алып шығып, бірінші теңдеуге қоямыз, сонда:
.

Графикалық әдіспен шешу. График салуды жеңілдету мақсатымен деп
аламызда мына теңдеуге келеміз..

4.1.1- сурет

функциясының графигін саламыз түзуі және сынған түзу
(4.1.1- сурет).График бойынша қиылысады, онда . Жүйедегі екінші
теңдеуге қойып, табамыз.

Жауабы: 5

Тапсырма 4.1.2 Теңдеулер жүйесін шешіңіз:

Шешуі:

1) болсын, онда

2) болсын, онда , .

Осы жағдайда, бастапқы жүйе мынадай түрге келеді:

Шыққан жүйенің шешімі жұбы болады. Бірақ бұл жұп шартын
қанағаттандырмайды, сондықтан қарастырылып отырған аймақта бастапқы жүйенің
шешімі болмайды.

3) болсын. Онда болады.

Осыдан берілген жүйе түріне келеді.

(14; 5) жұбы шыққан жүйенің шешімі болады.Бірақ бұл шешім
шартын қанағаттандырмайды. Осыдан бастапқы жүйенің бұл аймақта шешімі
болмайды. болсын. Онда болады. Қарастырылып отырған жүйе бұл
жағдайда түріне келеді, соңғы жүйенің шешімі (-18; 5) жұбы
болады. Бұл жұп шартын қанағаттандырады. Бұдан осы жұп бастапқы
жүйенің шешімі болады. Сонымен берілген теңдеулер жүйесі (2;-1), (-18;
5)шешімдеріне ие болады.

Жауабы: (2; -1), (-18; 5)

Тапсырма 4.1.3 Теңдеулер жүйесін шешіңіз:

Шешуі:

х0у сандық жазықтығын 2х-у=0 және х=0 түзулерімен төрт бөлікке бөлейік
те, берілген жүйені әр бөлікте қарастырайық. а)

екі теңсіздікті қанағаттандыратын (0;-2) шешіміне келеміз. Яғни, бұл жұп
бастапқы жүйенің шешімі болады. б)

бұл жүйенің шешімі (-2;0) жұбы болады. Бірақ бұл жұп жүйенің
теңсіздіктерін қанағаттандырмайды. Яғни бастапқы жүйенің шешімі болмайды.

в)

алынған жүйенің шешімі (-2;-4) жұбы болады. Бұл жұп жүйенің
теңсіздіктерін қанағаттандырады. Сондықтан осы жұп бастапқы жүйенің шешімі
болады.

г)

алынған жүйенің у=х-2 түзуінің теңдеуін қанағаттандыратын кез келген
(х;у) жұптары болуы мүмкін. Осы шексіз көп жұптардың ішінен және
шарттарын қанағаттандыратын шешімді табу керек. теңдеуін
қойып аламыз. Бір жағынан бізде бар. Осыдан бастапқы жүйенің
шешімі сандық жұптары болады. Мұндағы әр аймақта табылған
бастапқы жүйенің барлық шешімдерін жинап, жауабына келеміз.
Мұндағы.

Жауабы: ,мұндағы.

Тапсырма 4.1.4 түрінде берілген теңдеулер жүйесін шешіңдер.

Шешуі:

Бұл жүйені шешудің үш тәсілін көрсетейік.

Бірінші тәсіл

Сандық жазықтықты , түзулерімен аймақтарға бөліп, төрт
жағдайды қарастырайық.

а) б)

в) г)

Екінші тәсіл

Бастапқы жүйенің екінші теңдеуінен өрнегін жүйенің бірінші
теңдеуіне қоямыз. Осыдан: ,

Сонғы теңдеуді екі және аралығында шешейік

жүйенің шешімі жоқ.

жүйенің шешімі болады. Енді екенін пайдаланып,
табамыз. Осыдан болады. Сонымен, бастапқы жүйенің шешімі
болады.

Үшінші тәсіл

екенін біле отырып, жүйенің екінші теңдеуіне байланысты
болады. және біле отырып, бір уақытта және
теңдіктері орындалғанда, осы модульдердің қосындысы 4- ке тең болады деген
қорытындыға келеміз. Осыдан бастапқы жүйенің шешімі болады.

Жауабы:

Тапсырма 4.1.5 Теңдеулер жүйесін шешіңіз:

Шешуі:

Берілген жүйе келесі жүйеге тепе- тең болады.

Бұл жүйе ( болғандықтан модульдің қасиеті бойынша келесі аралас
жүйеге тепе - тең:

Соңғы жүйе келесі жүйелер жиынтығына тепе – тең:

Бұл жиынтықтың бірінші жүйесі

жүйесіне тепе – тең.

Соңғы жүйенің барлық шешімдерін түрінде жазуға болады. Мұндағы t -
кесіндісіндегі кез келген сан.

Жиынтықтың екінші жүйесі жүйесіне тепе – тең.

Соңғы жүйенің шешімдер жиыны сандық жұптарынан тұрады, мұндағы а-
кесіндісіндегі кез келген сан. Сондықтан бастапқы жүйенің шешімдері
барлық

Жауабы:

Тапсырма 4.1.6 Теңдеулер жүйесін шешіңіз:

Шешуі:

Бұл жүйені дәстүрлі тәсілмен модульді ашу арқылы шешуге болады, бірақ
біз тиімдірек шешу тәсіліне келтіреміз.

Берілген жүйе симметриялы: егер біз айнымалылардың орындарын ауыстырсақ,
онда жүйе өзгермейді. Сондықтан екенін біле отыра
түрлендіреміз. Осыдан бір шешімін жинау және белгілі қасиеттерді
пайдаланып, басқа шешімдерін табамыз.

Жауабы: ,.

Тапсырма 4.1.7 Теңдеулер жүйесін шешіңіз:

Шешуі:

Екінші теңдеуден х-ті у арқылы өрнектеп, жүйенің бірінші теңдеуіне
қоямыз:

Бірінші теңдеуді модульдің анықтамасы бойынша ашып, шешеміз. Бұл теңдеу
келесі жиынтыққа тепе- тең:

Егер болса, онда , егер болса, онда болады.

Жауабы:

Тапсырма 4.1.8 Теңдеулер жүйесін шешіңіз:

Шешуі:

болсын. Онда

Бұл және у айнымалыларынан тұратын біртекті жүйе. Бірінші теңдеуді
3-ке көбейтіп, 4- ке көбейтілген екінші теңдеуді азайтайық: . Оны
-ға қатысты квадраттық түрде шешейік. жүйесі екі жүйе
жиынтығына тепе- тең:

және

екенін біле отырып, табамыз

Жауабы:

Тапсырма 4.1.9 а-параметрінің әр мәнінде жүйесі бір ғана
шешімге ие болатындай мәнін табыңыз

Шешуі:

Егер берілген жүйенің шешімі болса, онда - да жүйенің шешімиі
болады. Сондықтан шешімнің жалғыз болуының шарты болады. Осы кезде
жүйе келесі түрге ие болады:

немесе

Әр табылған а- ның мәнінде жүйенің неше шешімі болатынын тексерейік.
болсын. Бастапқы жүйе келесі түрге келеді.

Жүйенің бірінші теңдеуін қарастырайық және теңсіздіктері
орындалғандықтан (жүйенің екінші теңдеуінен шығады), бұл теңдеудің сол жағы
әрқашан нольден үлкен немесе тең болады. Басқа жағынан жүйенің, екінші
теңдеуінен шығатын шартынан келеміз.

Яғни, теңдік немесе болғанда ғана орындалады.

жұбы жүйенің екінші теңдеуінің шешімі болатыны анық. Яғни
есеп шартын қанағаттандырады.

Егер болса, онда бастапқы жүйе келесі түрде жазылады:

Бұл жүйенің шешімі болатын сандарының кем дегенде үш жұбы болады:
Яғни, есеп шартын қанағаттандырмайды.

Жауабы:

Тапсырма 4.1.10 теңдеулер жүйесінің бір ғана шешімі болатындай, а-
параметрінің барлық мәндерін тап. Осы шешімді табу.

Шешуі:

Алдымен, егер сандар жұбы берілген теңдеулер жүйесінің шешімі
болса, онда

сандар жұбы да бұл жүйенің шешімі болатынына назар аударайық.

Бұдан, егер берілген жүйенің бір ғана шешімі болу керек болса, онда бұл
шешім жұбы болады. Себебі, болғанда ғана болады.

Егер берілген теңдеулер жүйесіндегі х- ті 0- ге ауыстырсақ, онда
жүйесіне келеміз. Бұдан болады. Осыдан , егер немесе .
Берілген жүйенің бір ғана шешімі болуының шарты немесе болады.

1) болсын. Онда берілген жүйе келесі түрде беріледі.

Екінші теңдеуден шығатындықтан, онда бірінші теңдеуден
болатынын табамыз. Екінші теңдеуден шығады. Екі теңдеуде де
болғанда ғана, болады. Сонымен, егер болса, жүйенің бір ғана
шешімі болады.

2) Енді болсын. Онда берілген жүйе түрге келеді.

Соңғы теңдеудің бірден көп шешімі болатынын оңай көруге болады, Мысалы:
және .

Яғни, бастапқы теңдеулер жүйесі тек болғанда ғана бір шешімге ие
болады [7].

Жауабы: ; .

Тапсырма 4.1.11 а- параметрінің қай мәнінде жүйе бір шешімге ие
болады?

Шешуі:

а параметрінің мәні берілген жүйе жалғыз шешімі болатындай болсын.
Жүйе теңдеуіне енетін х функциясына қатысты жұптығына байланысты
жұбы да жүйенің шешімі болады. Есептің шарты бойынша, шешім жалғыз
болғандықтан, болады, бұдан болады.

мәнін бастапқы жүйеге қояйық. Осыдан: бұдан ,
немесе , .

мәні қанағаттандыратынын тексерейік. Мұндай а болғанда, келесі
жүйеге ие боламыз:

Жүйенің екінші теңдеуінен және шығады. Яғни, және,
және осы теңсіздіктердің біреуі қатал болса, оларды қосып, келеміз.
Сонда бізде теңдік орындалады. Осыдан және болады, тек қана
және болғанда, яғни берілген жүйенің жалғыз ғана шешімі
болады.

болғанда, жүйе түрге келеді.

Сонғы жүйенің кем дегенде екі және шешімі болатынын көруге
қиын емес. Сондықтан есепке шешім бола алмайды.

Жауабы:

Тапсырма 4.1.12 Теңдеулер жүйесінің жалғыз ғана шешімі болатындай,

а- параметрінің барлық мәндерін табыңдар.

Шешуі:

Ең алдымен жүйеге енетін барлық функциялар х- ке қатысты жұп екенін
көреміз. а- параметрінің ізделінді мәні, сандар жұбы- бастапқы
жүйенің көрсетілген а- мәнінің жалғыз шешімі.

Онда х аргументінің функциясының жұптығының айтылған қасиетіне сүйеніп,
жұбы да бастапқы теңдеулер жүйесінің шешімі болады. Бірақ біз үйенің
жалғыз шешімі жұбы болады деп жорамалдадық. Сондықтан ол
жұбымен сәйкес болу керек. Яғни шарты орындалу керек. Бұдан
болады [8].

Сонымен, а – параметрінің бастапқы мәні болса, онда оған сәйкес бастапқы
жүйенің шешімі түрде болады. Осы сандар жұбын берілген теңдеулердің
әрқайсысына қояйық:

Бұл жүйені шешіп, сандардың екі жұбын: және деп аламыз.

Сонымен, а – параметрінің ізделінді мәндері және болуы
мүмкін. Сондықтан осыдан көзіміз жету үшін, тексеріс жүргіземіз.
(тексереміз)

а) болсын, онда бастапқы жүйе

Бұл жүйені келесі түрде жазайық:

теңдеуінен және шығады.Ал бұл теңсіздіктер деген
қорытындыға келеді.

Соңғы екі теңсіздіктен теңдеуінің сол жағы төменгі жағынан 0
санымен шектелгеніне көз жеткіземіз, және сондықтан бұл теңдеу және
болғанда ғана орындалады.

және теңдеулерін және теңдеуін қарастыра отырып,
жалғыз шешімін табамыз. Осыдан ізделінді болып табылады.

б) болсын, онда бастапқы жүйе түрінде болады.

Сандарды айнымалының орнына қою амалы бұл жүйені, мысалы және
жұптары қанағаттандырады. Сондықтан есептің шарты бойынша мәні
ізделінді болмайды.

Жауабы:

Тапсырма 4.1.13 Төмендегі теңдеулер жүйесін қанағаттандыратындай
нақты сандардың екі жұбы болатындай, а параметрінің барлық мәндерін тап.

Шешуі:

П- парабола, теңдеуі берілген, L- қисық сынық, теңдеуі
берілген, L1 және L2- сәуле, теңдеуі берілген, және ,
,

L- түзуі (4.1.2- сурет).

теңдеулер жүйесін шеше отырып, L-түзуі мен П-параболасынның ортақ
нүктелерін табайық.

Осы жүйеден келеміз, яғни жүйе кез келген болғанда, жалғыз
шешімге ие болады. Бұдан l- түзуі П- параболасымен нүктелерінде
қиылысатыны шығады.

4.1.2- сурет

үш мүмкін жағдайын қарастырайық.

а) Егер болса, онда l- түзуі теңдеуін берді. Бұл түзу П-
параболасын нүктесінде қиылысады, l2 сәулесімен қиылысады, бірақ l1
сәулесін қимайды. Сондықтан болғанда, бастапқы теңсіздіктер жүйесінің
тура екі шешімі болады.

б) Егер болса, онда l- түзуі - осін оң ординаталы
нүктесінде қияды, сондықтан l1 және l2 сәулелеріменде қиылысады.

Алдымен парабола мен l1 және l2 сәулелерінің қиылысу нүктесі болатын
және А және В нүктелері өтетіндей мәнін табайық.

А және В нүктелерінің координаталары төмендегі теңдеулер жүйесінен
табамыз:

Осыдан теңдеуін аламыз. Оның түбірлері болады. х1 және х2
сандары- А және В нүктелерінің абциссалары, ал а мәні l- түзуі А және В
нүктелері өткендегі теңдеулерінің түбірі. Себебі, , онда
болады.

және болғанда, l- түзуі L сынығын екі нүктеде қияды, олардың
біреуі- L сынығы мен П- параболасының ортақ нүктесі. Сондықтан және
болғанда бастапқы теңдеулер жүйесінің тура екі шешімі болады.

Егер немесе болса, онда l- түзуі А және В нүктелері өтпейді
және L сынығын екі әр түрлі нүктеде қияды. Бұдан теңдеулер жүйесі үш әр
түрлі шешімге ие болатынын білеміз.

k, k1 және k2- l түзуі мен l1және l2 сәулелерінің сәйкес бұрыштың
коэффициеттері болсын. Онда болады.

Егер болса, онда l түзуі l2-ні қияды және k=k1 болғанда ғана l1-
ді қимайды. Яғни осыдан болды. Сондықтан болғанда,
бастапқы жүйенің тура екі шешімі болады.

Егер болса, онда l түзуі L сынығын П- параболасында жатпайтын екі
нүктеде қияды. Бұл жағдайда жүйенің әр түрлі үш шешімі болады.

болсын, онда болды, яғни kk1 , және сондықтан l түзуі
l1-ді қимайды да, l2-ні қияды. Бұл жағдайда жүйенің екі әр түрлі шешімі
болады.

в) болса, онда l түзуі Оу осі теріс ординаталы нүктеде қияды.
Егер болса, яғни болса, онда kk2 және kk2 болады. Бұл
жағдайда l түзуі l2 сәулесін қияды да l1 сәулесін қимайды, сондықтан
жүйенің екі әр түрлі шешімі болады

Сонымен, егер болса, онда l түзуі сынықты қимайды. Бұл жағдайда
жүйенің жалғыз шешімі болады [9].

Жауабы: .

Тапсырма 4.1.14 Төмендегі теңдеулер жүйесінің үш ғана шешімі болатындай,
а және в параметрінің барлық шешімін табыңдар.

Шешуі:

- берілген теңдеулер жүйесінің шешімі болсын, сонда - да оның
шешімі болады. Бұдан, берілген жүйенің шешімдерінің саны тақ болуының
қажетті шарты болды. Осы шарттан және жүйенің бірінші теңдеуінен
шығады, екіншісінен шығады.

Егер болса, онда жүйенің жалғыз шешімі болады және
болады. Керісінше, егер болса, онда үшін де жүйенің дәл сондай
(бұл жағдайда ) шешімі болады.

Келесі жағдайды қарастырайық . теңдеуі хОу жазықтықта көп
нүктелер бір жұбының шыңы нүктесінде, екінші жұбының шыңы
нүктесінде болатын екі жұп сәуледен тұратын у- тәуелсіздігі хОу
жазықтығында көптеген нүктелерді береді. (4.1.3- сурет) Жүйенің екінші
теңсіздігі а- радиусының нүктесіндегі ортасымен шеңберін анықтайды.
Бұл шеңбер абсциссасы осьтерін нүктесінде қиып өтеді.

1) делік, онда (4.1.3- суретте) бейнеленген екі жағдайда ғана
шеңбер сәулемен тура үш жалпы нүктеге ие бола алады. Олардың әрбіреуін
қарастырайық.

а) , - кез келген теріс сан.

в)

4.1.3- сурет

болғанда. Мұнда , теңсіздіктен болатынын көреміз.Сірә,

жүйенің теңсіздігі бұл мәндерінде орындалады.

2) жағдайларын қарастырайық

а) , қайда b- кез келген сан.

в)

шартынан, екенін көреміз, сондықтан жүйенің теңсіздігі
орындалған.

Берілген нәтижелерді біріктіріп, шешімге келдік.

Жауабы: , егер немесе , егер

Тапсырма 4.1.15 Теңдеулер жүйесін шешіңіз:

Шешуі:

Бір координаттар жүйесінде және (4.1.4- суреттін)
графиктерін жасайық.

4.1.4- сурет

Суреттен графиктердің қиылысу нүктелерінің координаталарын санап
екі жұпсандарға ие боламыз. Ақырғы жүйеге тура қою арқылы бұл жұп сандар
берілген теңдеулерді шешімге айналдырып көреміз. Шынында, болғанда
болады. Егер болғанда болады.

Онда біз жү.йенің жуық емес шешімін көрсете аламыз (ал біздің
білуімізше, графикалық әдіс жуық әдіс болып табылады) ал оның нақты шешімі
екі жұп сандар болады [10].

Жауабы: .

Тапсырма 4.1.16 Теңдеулер жүйесін шешіңіз:

Шешуі:

Айнымалы шама х пен у тәуелсіз болғандықтан, онда модульдік белгілерді
ашу үшін мынадай төрт жағдайды қарастыру керек.

а) б)

в) г)

а) егер немесе Бұл жүйе шексіз көптеген шешімге ие болады:
Енді шыққан шешімдер х,у- тің қарастырылған облыстарында болу үшін,
сондай t- ларды таңдау керек. Ол үшін жүйесін шешеміз және
аламыз.

б) егер немесе Бұл жүйенің бір шешімі бар , бірақ ол
х,у- ті қарастыратын облыстарда жатпайды және негізгі жүйенің шешімі
болмайды.

в) егер немесе Бұл жүйенің х,у қарастырылатын облыстарына
жатпайтын шешіміне ие болады. Сондықтан табылған шешім негізгі
жүйенің шешімі болмайды.

г) егер немесе Бұл жүйенің шешімдері жоқ.

Бастапқы теңдеулер жүйесін графикалық түрде шешкен ыңғайлы. Бірінші
теңдеуден шығарамыз және осы функцияның графигін саламыз (сызық).
Екінші теңдеуден шығарған және х- функциясы, у- аргумент деп санап,
графигін салу оңай (штрих-пунктуациялық сызық). АВ кесіндісінде бірінші
және екінші теңдеулерінің графиктері сәйкес, яғни жүйенің шексіз көп
шешімдері бар. Осы шешімдерді жазайық. Суреттен АВ кесіндісінің
нүктелерінің абциссаларының шартын қанағаттандыратыны көрініп тұр.
Бұл жағдайда функциясы түріне келеді. Жүйенің ізделінді
шешімдері Мұндай нәтиже ертерек аналитикалық түрде алынды.

4.1.5- сурет

Жауабы: ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.