Ықтималдықтар теориясы мен математикалық статистиканы оқытудың әдістемесі


Мазмұны
Кіріспе . . . 3
Негізгі бөлім
1 Ықтималдықтар теориясы пәнінің негізгі түсініктері
1. 1 Комбинаторика элементері. Орналастыру, алмастыру, теру . . . 6
1. 2 Кездейсоқ оқиғалар. Оқиғалардың түрлері . . . 7
1. 3 Ықтималдықтың классикалық анықтамасы . . . 8
1. 4 Ықтималдықтың геометриялық анықтамасы . . . 9
1. 5 Салыстырмалы жиілік. Статистикалық ықтималдық . . . 10
1. 6 Ықтималдықтың негізгі қасиеттері . . . 10
2 Ықтималдықтар теориясының қарапайым теоремалары, формулалары
2. 1 Үйлесімсіз оқиғалардың ықтималдықтарын қосу теоремасы . . . 12
2. 2 Ықтималдықтарды көбейту теоремасы . . . 13
2. 3 Толық ықтималдық формуласы. Бейес формуласы . . . 15
2. 4 Бернулли формуласы . . . 19
2. 5 Муавр-Лапластың локальдық және интегралдық теоремасы . . . 22
2. 6 Пуассонның жуықтап есептеу формуласы . . . 26
3 Кездейсоқ шамалар
3. 1 Кездейсоқ шаманың негізгі ұғымы 28
3. 2 Тәуелсіз және тәуелді оқиғалар. . 28
3. 3 Дискретті кездейсоқ шамалар . . . 29
3. 4 Үзіліссіз кездейсоқ шамалар . . . . 35
3. 5 Тәуелсіз тәжірибелердегі оқиғаның пайда болуының ең ықтимал
саны . . . 39
3. 6 Оқушыларды ықтималдықтар теориясы мен математикалық статистиканың негізгі ұғымдарымен таныстыру-сабақ жоспары . . . 40
Қорытынды . . . 47
Қолданылған әдебиеттер тізімі . . . 48
Кіріспе
Адам ойы мен қиялы өте шексіз. Жылдарға, ғасырларға кейіндеп те, ілгерілеп те алға оза алады. Саналы адам көрсем, білсем, үйренсем деп тұрады. Көрген, білгенінен ой түйіндейді, қорытынды шығарады. Математика, физикада қарастырылатын есептер көбінесе бір мәнді анықталады. Мысалы: қолымызбен тасты лақтырсақ, онда тастың орнын кез-келген уақыт кезеңінде анықтай аламыз. Бірақ ғылымның әр саласында,
техникада, шаруашылық саласында қолданылатын көптеген есептер бір мәнді анықталмайды. Мысалы: тиынды лақтырып, оның қай жағымен түсетінін нақты айтуға болмайды. Мұндай жағдайда осы сияқты есептерді шешуде белгілі бір нақты шешім айтуға болмайтын тәрізді көрінеді. Алайда бұл тәжірибеде керісінше. Ойын практикасы көрсеткендей тиынды неғұрлым көбірек лақтырсақ, солғұрлым әрекеттің жартысында елтаңба жағы түссе, енді жартысында цифр жағы түсетіні байқалды. Бұл кездейсоқ оқиға. Белгілі бір заңдылыққа байланысты. Міне осындай заңдылықтарды ықтималдық теориясы қарастырады. Ең қарапайым мысал ретінде тиын лақтыруды алдық. Бірақ ықтималдықтар теориясында бұдан да күрделірек есептер қарастырылады. Шаруашылықтағы маңызды мәселенің бірі аудан мен облысты байланыстыратын телефон жүйесін орнату. Бұл да таза ықтималдық есеп. Мысалы: мұнда орталықтан ауданға телефон жүйесін тарту үшін қанша сым қажеттігі белгілі болу керек. Өмірде мұндай мәселелер көптеп кездеседі. Осындай мәселелер өндіріс саласын жоспарлауда, зерттеулер жүргізуде қолданылады. Мысалы: сынып арасында өткізілетін
жарыстардың нәтижесі дәлірек болу үшін нәтижелер ондық үлеспен, жүздік үлеспен есептелінеді. Сонда әр сыныптың нәтижесі дәлірек болу үшін қанша таңбаға дейін алу керек деген сұрақ туындайды.
Неғұрлым сынақ көп жасалынса, солғұрым нәтиже дәл болатыны белгілі. Ал ол үлкен шығынға әкеледі. Міне, осы арада ықтималдықтар теориясы көмекке келеді. Адамның күнделікті өмірі, дүниені танып-білу барысы кездейсоқ оқиғаға толы. Бұл кездейсоқтықтар өмірдің даму заңдылығына кедергі келтірмейді, керісінше, кездейсоқтық пен заңдылық біріне-бірі әсер етіп, өмірдің дамуына себепші болады.
Диплом жұмысының құрылымы:
Бұл дипломдық жұмыс кіріспеден, 3 тараудан, қорытынды және пайдаланылған дерек көздерінен тұрады.
I тарауда ықтималдықтар теориясы пәнінің негізгі түсініктері туралы жазылған.
II тарау ықтималдықтар теориясының қарапайым теоремалары, формулаларынан құралады.
III тарау кездейсоқ шамалардың негізгі ұғымдары мен түрлерінен тұрады.
Тақырыптың өзектілігі ықтималдықтар теориясын оқыту қажеттілігінің маңызы адамның күнделікті өмірі, дүниені танып-білу барысы кездейсоқ оқиғаға толы болғандықтан, ондағы кездейсоқтық заңдылықтарын білуде.
Ықтималдықтар теориясы мен математикалық статистиканы оқытудың кәсіби-педагогикалық бағдарын күшейту және математика мұғалімдерінің сапасын арттыру, оқу процесінде тәуелсіз кездейсоқ шамалар ұғымдарын қалыптастыру, математикалық ойлау қабілетін ұштау және басқа да ғылым салаларында қолданылуын қалыптастыру мәселесі маңызды роль атқарады.
Ғылыми жаңалығы:
1) Математикалық ойлаудың психологиялық негізін ашып көрсету;
2) Ықтималдықтар теориясын оқытуда оқушылардың математикалық ойлауының мақсатты бағытта дамыту мәселелерін жүйелі қарым - қатынас және ойлау қызметі негізінде шешу. Оқушылардың математикалық ойлауының осындай жүйесі жасалынды, сол арқылы ықтималдықтар теориясын оқыту, дамыту мен тәрбиелеудің біріңғай теориясын қалыптастыруға теориялық мақсатты жүзеге асыруға болады және іс-тәжірибеде ықтималдықтар бойынша бағдарламалар, оқулықтар және әдістемелік құралдар шығару, оқушылардың ойлау қызметін және ғылыми танудың біраз әдістерін қабылдау;
3) Ықтималдықтар теориясы мен математикалық статистиканың теоремаларын анықтау, ой мен сезімнің ықтималдықтар теориясын оқыту үрдісінде оқушылардың математикалық ойлауына әсерін дамыту;
4) Оқушылардың математикалық ойлауын дамыту үшін есептер жүйесінің әдістемесін пайдалану;
5) Оқушылардың математикалық ойлау жүйесін дамытуда және жетекші педагогикалық шарттарды айқындауда болашақ математика мұғалімдерінің педагогикалық қызметке дайындығын, мұғалімнің кәсіби - педагогикалық қызметінің мазмұны мен құрылымын оқып үйрену.
Жұмыстың практикалық маңыздылығы математика курсын оқытуда ықтималдық теориясы мен статистика ұғымын беру арқылы математикалық статистика есептерінің қойылу шарты мен шешудің әдіс тәсілдерінің қолданылуын практикада жүзеге асыру.
Зерттеу объектісі орта мектеп математикасында ықтималдықтар теориясы және математикалық статистиканы оқыту барысында логикалық есептердің шешу жолдары; педагогтардың ғылыми жетістіктері мен озық тәжірибелері; педагогикалық және зерттеушілік тәжірибе.
Зерттеу пәні ықтималдық теориясы, статистика, экономикалық және социологиялық зерттеулер, биология, медицина, физика, геология, психология ғылымдары, ауа райын бақылау, т. б.
Жұмыстың методологиялық базасы математика және информатика әдістемелік кабинеті, Ш. Ш. Уәлиханов атындағы политехникалық институтының оқу залы, Көкшетау қаласындағы облыстық кітапханасы.
Дипломдық жұмыстың мақсаты:
Ықтималдықтар теориясын оқытуда жалпы білім беретін орта мектепте және педагогикалық жоғары оқу орындарында тәуелсіз кездейсоқ шамалар ұғымын қалыптастыра отырып, кездейсоқтықтың әдіс-тәсілдерін шешуді,
теориялық білімді практикамен байланыстыра отырып, жандандыру арқылы қазіргі талаптарға сай жоғары оқу орнына түсуге талапкерлердің білім сапасын жақсарту жолдарын қарастыру, оқушылардың логикалық ойлау қабілетін, математикалық мәдениетін дамыту, жеке тұлғаны тәрбиелеуде және дамытуда өз функцияларын атқара отырып жалпы педагогикалық мәнге ие болу, болашақ мұғалімдерді өз ойын жеткізе алатын тұлға қалыптастыру.
Дипломдық жұмыстың міндеттері:
Ықтималдықтар теориясы мен математикалық статистикада кездесетін ұғымдар мен анықтамаларды білу;
Заңдылықтарды, теоремаларды, негізгі қасиеттерді пайдалана отырып кез келген есептерді шығара білу;
Математикалық статистика есептерінің қойылу шарты мен шешуін үйрену;
Кейбір проблемаларды шешу үшін ықтималдық теориясы мен статистиканың әдістерін практикада қолдана білу;
Оқыту үрдісінде жеке тұлғаның танымдық мүддесін қалыптастырудың жолдарын білу.
Кездейсоқтық? Оны оқып үйрену не үшін қажет?-деп сұрайтын
боларсыздар? Шын мәнінде, адамдар, ерте кездің өзінде-ақ оқиға өмірдегі бір ерекшелік емес, қағида екендігін байқаған. Міне сондықтан да кездейсоқ құбылыстар туралы ғылым пайда болды. Кездейсоқтық заңдарын білу қажет. Осыған байланысты мынадай мысал қарастырайық. Барлық ірі елді мекендерде «медициналық жедел жәрдем» станциялары бар. Кенеттен және қатты ауырып қалған адамдарға жедел жәрдем көрсету қажет болатын уақытты алдын ала болжап айту мүмкін емес. Берілген уақыт аралығында мұндай ауруларға шақырулардың көптігі қандай болады? Дәрігер мен «жедел жәрдем» машинасына аурудың қасында қанша уақыт кідіруіне
тура келеді? Бір жағынан, аурулар жәрдемді өте ұзақ күтпеуі, екінші жағынан дәрігерлер құрамын өте тиімсіз пайдалану байқалмас үшін, кезекшілік кезінде қанша дәрігер және машина болуы қажет? Біз шақырту уақыттары, дәрігердің аурудың қасында болу ұзақтығы, машинаның «Жедел жәрдем» пунктінен, ауру тұратын үйге дейін жолда болу ұзақтығы . . . кездейсоқ болып табылатын әдеттегі жағдаймен кездесіп отырмыз. Демек, амал біреу ғана: бұл жәрдем шынында да шұғыл болу үшін, барлық кездейсоқтықты ескере білу керек. Міне, тіпті осындай күнделікті мәселе де кездейсоқтықты білуді талап етеді. Сондықтан да оны оқып үйрену қажет. Осындай практикалық жұмыстарда есептеу әдістерін қолдана білуге үйрену, жалпы математикалық білім деңгейімді жетілдіру, пән бойынша жүйелі білімімді қалыптастыру, өмірде кездесетін оқиғаларды сараптай білу менің міндетім болып отыр.
Математика-нақты ғылым, бір қарағанда кездейсоқтыққа ешқандай
қатысы жоқ. Бірақ, осы кездейсоқтықтың сандық сипаттамасын, ықтималдық ұғымын берген басқа емес, осы математика.
Ықтималдықтар теориясы өмірдегі кездейсоқтықтарды зерттеп, олардың заңдылықтарын ашады.
1 Ықтималдықтар теориясы пәнінің негізгі түсініктері
1. 1 Комбинаторика элементтері. Орналастыру, алмастыру, теру
Комбинаторика-математика тарауларының бірі. Мұнда элементтер жиынының әртүрлі комбинациялары қарастырылып, олардың сандары есептелінеді. Комбинаториканың үш түрін қарастырамыз:
Алмастырулар.
а және в екі элементтен, олардың ретін өзгертіп, екі алмастыру алуға болады; ав, ва.
Үш (а, в, с) элементтен 6 алмастыру алынады: авс, вас, вса, асв, сав, сва. Алмастырулар мына заңдылыққа бағынады:
екі элементтен 2 алмастыру, немесе 2! Алмастыру алуға болады, 3 элементтен үштен 6 алмастыру 6! Алуға болады, онда 4 элементтен төрттен 4!=24 алмастыру алуға болады т. с. с.
Анықтама. Алмастырулар деп, бір бірінен айырмашылығы орналасу ретінде ғана болатын элементтер комбинацияларын айтады. Сонымен, m элементтен m! алмастыру жасауға болады, оны Р m арқылы белгілейді:
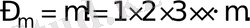
Орналастырулар.
Бір бірінен айырмашылығы орналасу ретінде немесе құрамында болатын n элементтің m-нен жасалған комбинацияларын орналастырулар деп атайды.
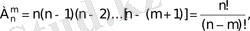
яғни
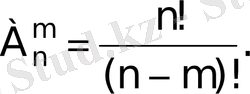
Мысал. 4 элементтен әрбіреуінде 2 элемент болатын комбинациялар құрып, оның санын есептеу керек. а, в, с, d элементтерінен екі-екіден
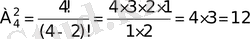
комбинация құруға болады. Олар ав, ас, аd, вс, сd, ва, са, dа, св, dв, dс.
Терулер.
Бір бірінен айырмашылығы құрамында (ең болмағанда бір элементі өзгеше болу керек) болатын n-элементтен m-нен жасалған элементтер комбинацияларын n-элементтен m-нен жасалған теру деп атайды.
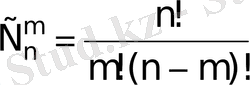
себебі
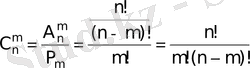
ЕСКЕРТУ. Теру комбинацияларында элементтердің реті қаралынбайды.
Мысал. 4 элементтен 2-ден жасалған теру саны
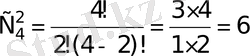 -ға тең.
-ға тең.
а, в, с, d: ав, ас, аd, вс, вd, сd.
1. 2 Кездейсоқ оқиғалар. Оқиғалардың түрлері
Ықтималдықтар теориясы кездейсоқ құбылыстардың заңдылығын зерттейтін математикалық ілім.
Ықтималдықтар теориясының негізгі ұғымдары-кездейсоқ оқиғалар және оқиғалардың ықтималдылығы ұғымы. Оқиға деп, кейбір байқау, тәжірибе, немесе эксперимент жасауда белгілі бір шарттардың жиынтығы орындалғанда пайда болатын, немесе пайда болмайтын нәтижені айтады. Оқиғаларды латын алфавитінің алғашқы бас әріптерімен белгілейді:
А, В, С, . . .
Оқиға үш түрге бөлінеді: ақиқат, мүмкін емес, кездейсоқ.
Ақиқат оқиға деп, белгілі бір шарттар жиынтығы орындалғанда міндетті түрде пайда болатын оқиғаны айтады. Мысалы, ойын сүйегін лақтырғанда 1-ден 6-ға дейінгі ұпайдың біреуінің түсуі ақиқат.
Мүмкін емес оқиға деп, белгілі бір шарттар тобы орындалғанда пайда болмайтын оқиғаны айтады. Мысалға, ойын сүйегін бір рет лақтырғандағы түсетін ұпай санының 6-дан көп болуы мүмкін емес.
Кездейсоқ оқиға деп, белгілі бір шарттар тобы орындалғанда пайда болуы да, болмауы да мүмкін оқиғаны айтады. Мысалы, «ойын сүйегін бір рет лақтырғанда 5 ұпай түсті» деген оқиға кездейсоқ оқиға болады.
Ықтималдыұтар теориясы осы кездейсоқ оқиғаларды зерттейді.
Кездейсоқ оқиғалар: үйлесімді, үйлесімсіз, жалғыз ғана мүмкіндікті және тең мүмкінді болып бөлінеді.
Егер тәжірибе нәтижесінде бір оқиғаның пайда болуы қалған оқиғалардың пайда болуына кедергі жасамас, онда мұндай оқиғаларды үйлесімді оқиғалар дейді. Мысалы, жәшікте бірнеше заводта жасалынған тек жоғары сортты бөлшектер бар. Таңдамай, қалай болса солай алынған бөлшектің:
а) жоғары сортты болуы; б) белгілі бір заводта жасалынған болуы-үйлесімді оқиғалар.
Егер тәжірибеде бір оқиғаның пайда болуы қалғандарының пайда болуына кедергі болса, ондай оқиғаларды үйлесімсіз оқиғалар дейді. Мысалы, теңгені бір рет тастағанда «герб» түсуі «цифр» түсуіне мүмкіндік бермейді (кедергі жасайды) . Сондықтан «герб түсті» және «цифр түсті» деген оқиғалар өзара үйлесімсіз.
Егер тәжірибе нәтижесінде пайда болған оқиға ақиқат оқиға болса, онда ол жалғыз мүмкіндікті оқиға деп аталынады. Теңгені бір рет тастағанда міндетті түрде жоғарыда аталынған екі оқиғаның бірі пайда болады. Сондықтан бұл оқиғалар жалғыз ғана мүмкіндікті.
Егер оқиғалардың пайда болу мүмкіндіктері бірдей деп есептелінсе, ондай тең мүмкіндікті оқиғалар дейді. Ойын сүйегін лақтырғанда 1-ден 6-ға дейінгі кез келген тең ұпайдыңпайда болуы тең мүмкіндікті оқиға . Себебі, ойын сүйегі біртекті материалдан жасалынған, цифрлар саны оның әрбір жағының салмағына әсер етпейтін, дұрыс көпбұрыш деп есептелінеді.
1. 3 Ықтималдықтың классикалық анықтамасы
Ықтималдық ұғымы ықтималдықтар теориясының негізгі ұғымдарының бірі екендігі айтылады. Ықтималдықтың бірнеше анықтамасы бар, соның бірін беру үшін мынадай мысал қарастырылады:
Жәшікте мұқият аралстырылған 7 шар бар болсын, оның үшеуі қызыл, екеуі ақ, қалған екеуі көк. Жәшіктен қалай болса солай бір шар алынған. Алынған шардың түрлі түсті (қызыл не көк) болу мүмкіндігі (оқиға А), оның ақ шар болу мүмкіндігінен (оқиға В) үлкен. Біз ынта білдіріп отырған оқиғаның (А) пайда болатын жағдайларын А оқиғасына ҚОЛАЙЛЫ жағдайлар (оқиғалар) дейді. Қарастырылып отырған мысалда А оқиғасының пайда болуына қолайлы жағдайлар саны бесеу, ал барлық мүмкін болатын элементар жағдайлар саны жетеу.
Анықтама. А оқиғасының ықтималдылығы Р(А) деп, осы оқиғаға қолайлы жағдайлар санының (m) барлық жағдайлар санына (n) қатынасын айтады, яғни
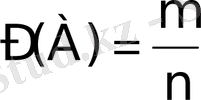
Бұл анықтаманы ықтималдықтың классикалық анықтамасы дейді.
Анықтаманы алдыңғы қаралған мысалға қолдансақ, онда m=5, ал n=7 болады да, түрлі түсті шар алу ықтималдылығы
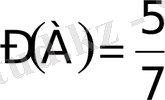 болады.
болады.
Классикалық анықтама бойынша анықталған ықтималдықтың мынадай қасиеттері бар:
- Ақиқат оқиғаның ықтималдылығы бірге тең, яғни Р(А) =1, егер А-ақиқат оқиға болса. Себебі, ақиқат оқиғалардың пайда болуына барлық жағдайлар қолайлы.
- Мүмкін емес оқиғаның ықтималдылығы нөлге тең, Р(А) =0, егер А-мүмкін емес оқиға болса. Расында мүмкін емес оқиғаның пайда болуына ешбір жағдай қолайлы емес.
- Қандай да болмасын оқиғаның ықтималдылығы нөл мен бірдің арасында жатқан нақты сан.
0 ≤ Р(А) ≤ 1
А-кездейсоқ оқиға болса, онда А-ға қолайлы жағдайлар саны m барлық жағдайлар саны n-нен кіші, яғни 0 ≤ m ≤ n осыдан 0 ≤ Р(А) ≤ 1 шығады.
Мысал. Бір колода құратын 36 карта мұқият араластырылған, яғни әрбір картаның орналасу мүмкіндігі тең ықтималды.
Колодадан алынған бір картаның тұз болу; Бірінен соң бірі алынған екі картаның екеуі де тұз болу ықтималдылығын табу керек.
Шешуі. 1) Т 1 (тұз пайда болуы) оқиғасына қолайлы элментар жағдайлар саны m=4, ал барлық тең мүмкінді жағдайлар саны n=36, Сондықтан, іздеп отырған ықтималдық
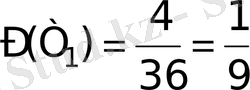
2)
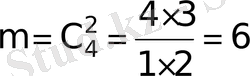 , ал
, ал
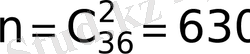
болады да, ізделініп отырған ықтималдық
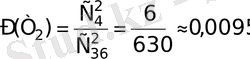
Бұл есепті шығаруда
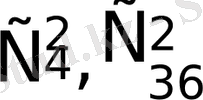 сияқты шартты белгілер қолданылады, ол белгілер терулер санын көрсетеді. Терулер ұғымы комбинаторика ұғымына жатады.
сияқты шартты белгілер қолданылады, ол белгілер терулер санын көрсетеді. Терулер ұғымы комбинаторика ұғымына жатады.
1. 4 Ықтималдықтың геометриялық анықтамасы
Алдыңғы тақырыпта біз тәжірибенің ақырлы санға тең теңмүмкіндікті нәтижелер бойынша оқиғаның ықтималдығын анықтадық.
Ал егер нәтижелер саны ақырсыз болса не істейміз? Мұндай жағдай кейбір геометриялық есептеулерде кездеседі.
Мысал 1: Әлемнің географиялық картасында (мысалға көзімізді жұмып) кездейсоқ нүктені көрсетейік. Бұл нүктенің Қазақстан жері болып шығу ықтималдығы қандай? Бұл сұраққа жауап беру үшін Қазақстан әлем картасының қанша бөлігін алатынын білу қажет. Яғни картаның барлық ауданының Қазақстан қанша бөлігін алатынын білу қажет. Бұл аудандардың қатынасы ізделінді ықтималдықты береді. Берілген бір шектелген облысты деп белгілейік. Егер облысының кез келген нүктесіне түсу теңмүмкін болса, онда кездейсоқ нүктенің берілген А жиынына түсу ықтималдығы аудандардың қатынасына тең болады:
мұндағы Р - ықтималдық, S - аудан. Бұл ықтималдықтың геометриялық анықтамасы.
Мысал 2: Жазықтықта шеңбер және шеңбер ішінде үшбұрыш берілсін. Шеңбер ішінен бір нүкте алайық. Онда нүктенің үшбұрышта жату ықтималдығын қалай анықтаймыз?
Мысал 3: Дәптерге салынған бұрышты транспортирмен өлшегенде, оның 900 -тық бұрыштың өлшемінде жату ықтималдығы қандай?
Шешімі:
m=900 -тық бұрыштың өлшемінде жатуы
n=1800 -тық бұрыштық өлшемі
1. 5 Салыстырмалы жиілік. Статистикалық ықтималдық
Салыстырмалы жиілікте анықтама беру үшін мынадай мысал қарастыралық. n рет тәжірибе қайталанып жүргізілді делік, әр тәжірибеде А оқиғасының пайда болған, болмағанын есептеп отыралық. Сонда n тәжірибеде А оқиғасы m реет пайда болсын. А оқиғасының пайда болу санының тәжірибенің қайталану санына қатынасын,
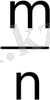 бөлшегін, А оқиғасының пайда болу
жиілігі
деп атайды.
бөлшегін, А оқиғасының пайда болу
жиілігі
деп атайды.
Тәжірибенің қайталану саны мейлінше үлкен болғанда жиілік тұрақты бір санның төңірегінде (маңайында) тығыз топталады екен. Осы заңдылықты статистикалық тұрақтылық деп атайды.
Мысалға, XVIII ғасырда француз ғалымы Бюффон, үлкен сандар заңын тіжірибе арқылы тексеру кезінде, теңгені 4040 рет лақтырғанда «герб» 2048 рет пайда болған, сонда «герб» түсу жиілігі
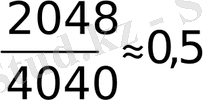 -тің маңайына болатынын анықталған. Сонымен, салыстырмалы жиілік W(A) деп, жасалынған тәжірибеде А оқиғасының пайда болған санының (m) барлық қайталанған тәжірибе санына (n) қатынасын айтады.
-тің маңайына болатынын анықталған. Сонымен, салыстырмалы жиілік W(A) деп, жасалынған тәжірибеде А оқиғасының пайда болған санының (m) барлық қайталанған тәжірибе санына (n) қатынасын айтады.
W(A) =
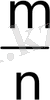
Мысалдар.
1. 100 рет оқ атылғанда, нысанаға 76 рет тигені (А) байқалды. Нысанаға оқтың тию «жиілігі» қандай ?
Шешуі. Мұндағы m=76, n=100, ендеше
W(A) =
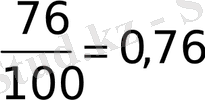
2. Техникалық бақылау бөліміне түскен 100 пар аяқ киімнің төртеуі жарамсыз болып шықты. Жарамсыз аяқ киімдердің салыстырмалы жиілігі қандай?
Шешуі. n=100, m=4, онда
W(A) =
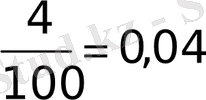
Ықтималдықтың классикалық және статистикалық анықтамаларын салыстыра отырып, мынадай қортындыға келуге болады: ықтималдықтың классикалық анықтамасы тәрибенің шындығында болуын талап етпейді, ал салыстырмалы жиіліктің анықтымасы (статистикалық анықтама) тәжірибеде жасалынған деп ұйғарып есептелінеді. Басқаша айтқанда, ықтималдық тәжірибеге дейін, ал жиілік тәжірибеден кейін есептелінеді.
1. 6 Ықтималдықтың негізгі қасиеттері
1. 0!=1
Equation. 3, бұл теңдік 0!=1 болғанда ғана орындалады, себебі
Equation. 3
Шынында, m-элементтен m-нен жасалатын теру саны 1-ге тең.
2.
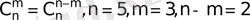 ,
,
болса
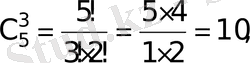
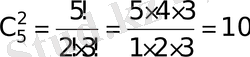 .
.
3.
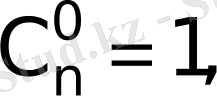
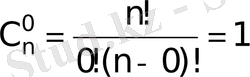 Equation. 3
Equation. 3
Мысал. Спортлото (36-дан 5) ойынына қатысушы бір билет сатып алған. Оны толтыру жағдайлары нешеу және ұту ықтималдығы қандай?
Шешуі. Бір билет толтыру үшін ойын ережесі бойынша 1-ден 36-ға дейінгі натурал санның бесеуін сызу керек. Сызу тәртібі әртүрлі, оның саны

Сонымен, ұтысқа қатысатын тең мүмкінді жағдайлар саны n=376, 992. Бір билет иесінің ұту ықтималдығы.

2 Ықтималдықтар теориясының қарапайым теоремалары
2. 1 Үйлесімсіз оқиғалардың ықтималдықтарын қосу теоремасы
Теорема. Екі үйлесімсіз оқиғаның қосындысының ықтимадығы ол оқиғалардың ықтималдықтарының қосындысына тең.
Р(А+В) =Р(А) +Р(В)
Салдар. Егер А 1 , А 2 , . . . , А n парланған үйлесімсіз оқиғалар болып, онда бұл оқиғалардың қосындысының ықтимадығы әрбіреуінің ықтималдықтарының қосындысына тең болады, яғни
Р(А 1 +А 2 +…+А n ) =P(A 1 ) +P(A 2 ) +…+P(A n )
1 мысал. Кәсіпорыннан шығатын бұйымның, орта есеппен, 21 %-і жоғары сортқа, 70% бірінші сортқа жатады. Таңдамай алынған бір бұйымның бірінші немесе жоғарғы сортқа жату ықтималдығы қандай?
Шешуі. А-алынған бұйым жоғарғы сортты, В-алынған бұйым бірінші сортты. Олардың ықтималдығы Р(А) =0, 21, Р(В) =0, 7. А және В оқиғалары үйлесімсіз, себебі бір тәжірибеде екеуі бірдей бірге пайда бола алмайды. Сондықтан бұл оқиғалардың ықтималдығы үшін қосу теоремасы орындалады:
Р(А+В) =Р(А) +Р(В) =0, 21+0, 7=0, 91
Сонымен ізделінді ықтималдық Р(А+В) =0, 91
Жауабы 0, 91
2 мысал. өндіріс практикасы үшін 30 студентке Шымкенттен 15 орын, Қостанайдан 8 орын және Ақтөбеден 7 орын бөлінген. Белгілі бір екі студент үшін, практиканы өтуге, бір қалаға бару ықтималдығы қандай?
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz