Maple 7 жүйесі мүмкіндіктерімен таныстыру

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:

Кіріспе.
Дипломдық жұмыстың өзектілігі: XX ғасырдың екінші бөлігінде компьютер адам өміріне кіре бастады. Көптеген математикалық есептер аналитикалық түрде есептеліп, оның әртүрлі координаталық жүйелерде сиппаттала бастады. Тез, ыңғайлырақ шығарылатын есептердің саны күрт өсті. Құбылыстар аса күрделі формулалармен сипатталғанымен, олардың нәтижесі компьютермен бірнеше секунд не минут ішінде шығарылады. Әлемді деңгейде өзінің қуаттылығын көрсете алған Maple 7 жүйесі бұл дипломдық жұмыста қарастырылады. Maple 7 жүйесінің мүмкіндіктері өте көп. Оның ішінде Maple 7 жүйесі әртүрлі аналитикалық түрде жазылған функциялардың графиктерін сала алады, математикалық анализ курсындағы функциялардың шегін табу, қатарлардың қосындыларын табу, туындыларды есептеу, интегралдарды шешу, теңдеулерді шешу, теңсіздіктерді шешу т.б. сұрақтарға жауап бере алады. Дипломдық жұмыста үш өлшемді функциялардың графиктерін салу қарастырылады. Үш өлшемді функцияларды Maple 7 жүйесінде жеңіл салу көрсетілген. Студенттер, оқушылар функцияларды зерттеуде графиктерін салады. Ол функциялардың өсуі, кемуі, иілу нүктелері, дөңестігі, ойыстығын зерттейді. Ал осы жүйе арқылы тез, оңай салуға болады.
Зерттеу объектісі жоғарғы сыныптарда үш өлшемді функциялардың графиктерін құру болып табылады.
Зерттеу пәні математикалық талдау курсы бойынша үш өлшемді функциялардың графиктерін Maple бағдарламасында игеру.
Міндеттері:
1. Үш өлшемді функциялардың графиктерн бағдарламада көрсету
2. Maple 7 бағдарламасында графиктердің өзгеру параметрін көрсету
3. Графиктердің анимациялық өзгеруін көрсету
4. Үш өлшемді фигураларды масштабтау және бұрыштарын өзгерту
Дипломдық жұмыстың мақсаты Оқытудың несиелік жүйесіндегі оқитын студенттерді және оқушыларды Maple 7 жүйесі мүмкіндіктерімен таныстырып, математикалық есептерді бұл жүйеде модельдеуге үйрету. Дипломдық жұмыстың мақсаты үш өлшемді функциялардың графиктерін құру, оларды салыстыру, анимациялық графиктерді құру болып табылады.
Maple 7 жүйесі мынадай типті есептерді шығара алады:
1) көптеген үш өлшемді функциялардың графиктерін салу;
2) теңдеулер жүйесін шеше алады, яғни теңдеудің түбірін табу.
3) функцияның экстремум нүктелерін табу;
4) көптеген үш өлшемді функциялардың анимациялық графиктерін салу;
5) дифференциалдық теңдеулерді шешу;
6) функцияның туындысын табу (бірінші ретті, екінші ретті, жоғарғы ретті);
7) анықталған, анықталмаған интегралдарды шешу;
8) екі еселі, үш еселі интегралдарды есептеу және т.б.

Дипломдық жұмысым кіріспе, екі бөлімнен, қорытынды және қолданылған әдебиеттер тізімінен тұрады. Оның бірінші бөлімінде көп айнымалы функция ұғымы, функцияның анықталу облысы, тақ-жұптығы, функция туындысы және дифференциалы, дөңес функциялар және иілу нүктелері, функцияның графигін салу, функцияның өсуі мен кемуі, функцияның дөңестігі мен ойыстығы жайында айтылған. Ал екінші бөлімі Maple 7 жүйесінің теориялық мағлұмат берілген. Элементтің маңызды командасын және көлемді графиктердің мүмкіншілігі көрсетілген. Бұл мағлұматты қолдана отырып, әр түрлі математикалық есептерді модельдеу, математикалық есептерді тез, жылдам шешу сұрақтары қарастырылған. Үш өлшемді графиктердің бұрылу бұрыштарының айырмашылықтарын көреміз. Сондай - ақ графиктер Декарт координата жүйесімен ғана емес, сфералық жүйеде де, полярлық жүйе де де салуға болады.

1. Көп айнымалы функциялар

0.1 Көп айнымалы функциялар. Анықталу және мәндер облысы

Анықтама 1.1: Егер Х жиынында жатқан әрбір (х1, х2, ..., хn) тобына белгілі бір заңдылықпен z айнымалысының мәні сәйкес келетін болса, онда z=f(х1, х2, ..., хn) - көп айнымалы функциясы берілді дейді.
Мысалы, цилиндр ауданын көрсететін z = х1[2]х2 формуласы екі айнымалы функцияны береді. Мұнда х1 - табанының радиусы, ал х2 - биіктігі.
х1, х2, ..., хn айнымалылары тәуелсіз айнымалылар немесе аргументтер деп, ал z - тәуелді айнымалы немесе функция деп аталады. f таңбасы сәйкестік заңын анықтайды.
Х жиыны функцияның анықталу облысы деп аталады.
Z жиыны функцияның мәндер облысы деп аталады..
Екі айнымалы функция: z = f (х, у), z = (х, у), z = z (х, у) және т.с.с. деп белгіленеді.
Сонымен қатар екі айнымалы функциялар үшін құралған барлық ұғымдар мен теоремалар көп айнымалы функциялар үшін де оңай көшіруге болады.
(х, у, z) үш өлшемді кеңістігінде жатқан z аппликатасы х және у айнымалыларымен z = f (х, у) теңдігі арқылы байланысқан нүктелердің жиыны z=f(х,у) функцияның графигі деп аталады.
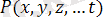
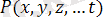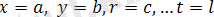
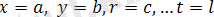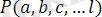
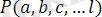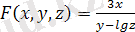
Көп өзгеріске ұшырайтын функция сондай-ақ белгіленеді . Мысалы, егер 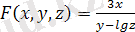және .
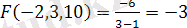
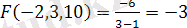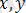
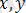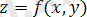
Геометрияда екі айнымалы олар жазықтықта тек нүкте болып белгіленеді, ал функцияда бұл екі айнымалы 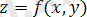кейде жоғары кеңістікте; ол үш айнымалыға тең x,y,z нүктемен белгіленеді (әдетте бұл айнымалылар абсцисса, ордината, апликата нүктелерімен сондай-ақ тең бүйірлі жүйені координата ретінде қарастырылады).
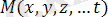
Төрт немесе одан да көп санды айнымалы геометрияда өзіне лайықты көрініс таба алмайды. Бірақта, жеңілдету жазбаны ашу үшін жүйеде кез келген n айнымалы нүкте деп, ал n кеңістік аймағы дейді 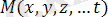a функциясында ал n айнымалысына бағынышты, сондықтан ол функцияны n нүктесіне сәйкес кеңістік дейді .
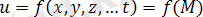
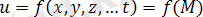Анықталу аймағы функцияда барлық нүктелердің жұптасуы болсада, бірақта олар анықталу аймағында соншалықта орын алмайды.
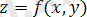
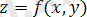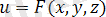
Екі айнымалы үшін функцияда анқталу аймағына бірнеше кеңістіктегі жұп нүктелері қажет және сондай-ақ үш айнымалы үшін 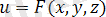керек.1
Мысал 1. Функцияның дербес мәнін табыңыз:
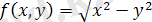
1) 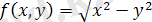мұндағы ;
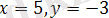
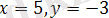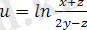
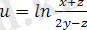
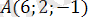
2) 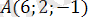нүктесінде
Шешуі.1)
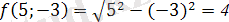
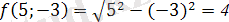
2) .
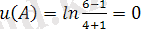
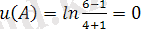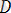
Мысал 2. Келесі теңсіздікпен берілген x және y айнымалылырының 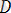өзгеру облысын салыңыз:
1)
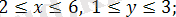
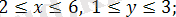
2)
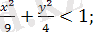
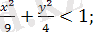
3)
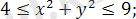
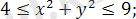
4)
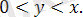
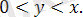
Шешуі. 1) Берілген теңсіздіктерді қанағаттандыратын тіктөртбұрыштың қабырғалары 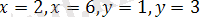түзулер болатын және осы түзулердің ішінде жататын барлық нүктелер 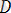облысы болады.
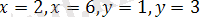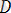
Бұл тікбұрыштағы аймағынының өзгеруі x және y (Сурет 1.1.1).

Сурет 1.1.1
Мұндай аймақ, яғни мына тікбұрыштың ішіне кіретін жабық аймақ дейді.
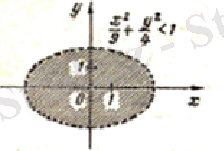
2) Мұндағы облысы 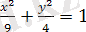эллипстің ішінде жатқан нүктелер, себебі бұл нүктелер берілген теңсіздікті қанағаттандырады.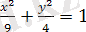( Сурет 1.1.2). Осындай аймақ, яғни осы тікбұрыштың ішіне кірмейтін аймақты ашық аймақ дейді.

Сурет 1.1.2
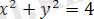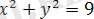
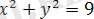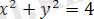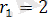
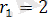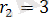
3) Мұндағы аймағы және шектелген дөңгелек шеңбер координаталар басында жататын ортақ центрі бар және радиустары және 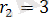тұйық аймаққа сәйкес келеді (Сурет 1.1.3).

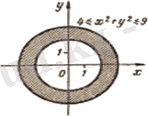
Сурет 1.1.3
4) Мұндағы (ашық) аймақта бірінші координата бұрышындағы және абсцисса осіне биссектриса болып келеді (Сурет 1.1.4).

Сурет 1.1.4
Мысал 3. Келесі функциялардың анықталу облысын табыңыз:

1) ;
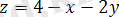2) ;
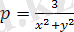
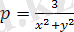3) ;

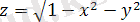
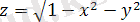4) ;
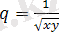
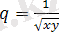5) ;
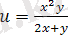
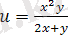6) .

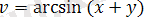
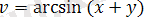Шешуі:
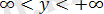
1) z функциясы кез келген бүтін рационалды функция, кез келген x және y міндерінде анықталған, яғни z функциясының анықталу облысы ол барлық сандық xОy жазықтығы, , 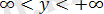. Бұл функцияның геометриялық көрінісі (графигі) жазықтық болады, яғни ол А(4;0;0), В(0;2;0), және С(0;0;4) нүктелерінде координата осьтарын қиып өтеді.
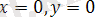
2) p функциясы x,y кез келген мәнінде табуға болады, тек қана 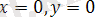. жүйесінде орындалмайды. Себебі, ол анықталу облысында p функциясы барлық сандық мәнге сәйкес, тек қана (0;0) емес.
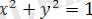
3) z функциясының анықталу облысы координата басы центрі болатын және радиусы r=1 шеңбер, 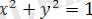шеңбердің шеткі нүктелерін қоса алғанда. Ал шеңберде ішкі түбірі оң, ал оның шеті 0-ге тең, ал дөңгелек сыртында ол теріс. Графикалық суретте функция хОу жазықтығында орналасқан жартылай сфера болып беріледі (Сурет 1.1.5)

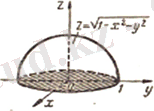
Сурет 1.1.5
4) q функциясы 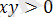теңсіздігін қанағаттандыратын хОу жазықтығын айтамыз 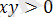. Барлық осы нүктелер бірінші және үшінші квадраттың ішінде берілген (ашық анықталу аймағы).
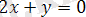
5) u функциясының анықталу облысы жазықтығы хОу болады, 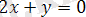түзуін жазықтықтан алып тастаймыз.
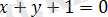
6) функциясының анықталу облысы х және у жақын, қанағаттанарлық хОу жазықтығында жолақпен беріледі, параллель түзуд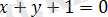е және (Сурет 1.1.6).

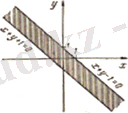
Сурет 1.1.6

1.2 Екі айнымалы функцияның шегі мен үзіліссіздігі

Анықтама 1: Егер кез келген оң, тіпті мейлінше кіші саны үшін
f (х, у) - А (1.2.1)
теңсіздігі барлық 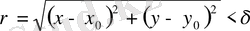теңсіздігін қанағаттандыратын (х, у) нүктелері үшін орындалатындай саны табылатын болса, онда А саны f(х,у) функциясының х х0 және у у0 (немесе (х;у) нүктесі (х0; у0) нүктесіне) ұмтылғандағы шегі деп аталады.
Бұл шек былай жазылады: 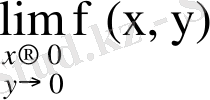=А
Мысал 1: 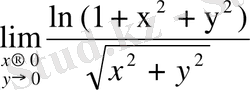шегін табамыз.
Шешуі: 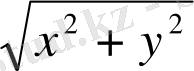= деп белгілейміз. Онда х 0, у 0 шарты 0 шартына теңбе-тең болады.
=

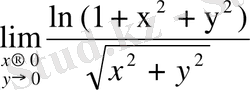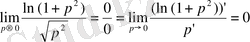
Анықтама 2: z = f (х, у) функциясы үшін төмендегі үш шарт орындалсын:
1. f (х, у) функциясы (х0, у0) нүктесінде;
2. х х0 және у у0 болғандағы ақырлы шегі бар.
3. шегі функцияның (х0, у0) нүктесіндегі мәніне тең, яғни
=f(х0,у0) (1.2.2)
Онда z = f (х, у) функциясы (х0, у0) нүктесінде үзіліссіз дейді.
Егер функция аргументінің шексіз аз өсімшесі функцияның өсімшесімен сәйкес келсе ғана және тек сонда ғана функция үзіліссіз болады, яғни .

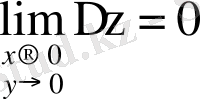Мысал 2. Шектерді есептеңіз:
1) 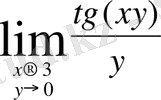; 2)
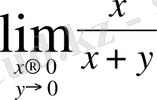
Шешуі.
1) 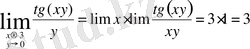, сондықтан .
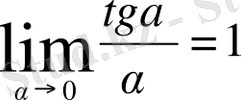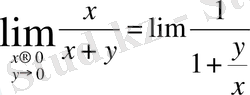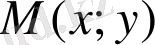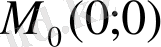2) - функция қатысты болады да, бірақта және нүктелерінде шектеулі бола алмайды, ал егер 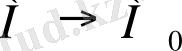басқа түзуде болса, онда 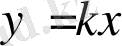, 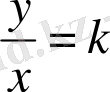т.с.с. олар берілген коэффициентке байланысты, яғни М нүктесі орналасқан нүктесінде.2

1.3 Функцияның дербес туындысы

х және у аргументтерінің сәйкесінше ∆х, ∆у өсімшелерін қарастырамыз. Сонда ∆z = f (х + ∆х; у + ∆у) - f (х, у) шамасы f(х; у) функциясының толық өсімшесі деп аталады. Функцияның дербес туындылары келесі түрде белгіленеді:
Егер тек х аргументіне немесе тек у аргументіне ғана өсімше беретін болсақ, онда сәйкесінше алынған ∆хz=f(х+∆х;у) - f(х;у) және ∆уz=f(х;у+∆у) - f(х;у) функциялардың өсімшелері дербес деп аталады. Функцияның толық өсімшесі дербес өсімшелердің қосындысына тең болмайды, яғни
∆ z != ∆хz + ∆уz (1.3.1)
Анықтама 1: Көп айнымалы функцияның бір айнымалысы бойынша дербес туындысы деп функцяның дербес өсімшесінің қарастырылып отырған тәуелсіз айнымалысына қатынасының шегін атайды, мұндағы тәуелсіз айнымалы нөлге ұмтылады.

zx'=lim∆x--0∆xz∆x=lim∆x--0fx+∆x,y -f(x,y)∆x (1.3.2)
zy'=lim∆y--0∆yz∆y=lim∆y--0fx,y+∆y -f(x,y)∆y (1.3.3)

Дербес туындылардың (1), (2) анықтамаларынан мынадай тұжырым шығаруға болады: zх' (х; у) туындысын табу үшін у айнымалысын тұрақты деп есептеп, ал zу' (х; у) туындысын табу үшін х айнымалысын тұрақты деп санау керек.
Мұндай жағдайда белгілі дифференциалдау ережелері түгелімен сақталады.
Мысалы: Келесі функциялардың дербес туындыларын тап:
а) z = х[2] + у[2] және
b) z = х ln у +
у

х
Шешуі: а) z = х[2] + у[2]
zх' = 2х; zу' = 2у
b) z = х ln у +
у

х

zх' = ln у + у(
1
)' = ln у -
у

f(r) скаляр өрісінің градиент ұғымын енгізейік. M(r) нүктесіндегі f(r).=f(x,y,z) скалярлық өрісінің градиенті деп проекциясы тік бұрышты координаттар жүйесінде 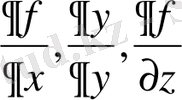тең болатын векторды айтамыз.
f(x,y,z) скалярының градиенті grad f символымен белгіленеді.
Сонымен, grad f=.
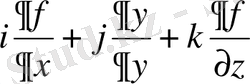grad f векторының модулі: = 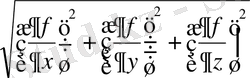тең болады.
Анықтама: Егер Р(х,у) және Q(x,y) функциялары және олардың 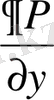және 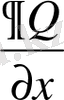дербес туындылары тұйық G облысында үздіксіз болса, онда Pdx+Qdy өрнегі 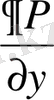= 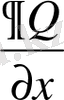болғанда және тек сонда ғана қандай да бір функцияның осы облыстағы толық дифференциалы болып табылады.
Мысал 1. Функцияның дербес туындыларын табыңыз:
1)
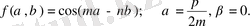
2)
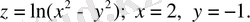
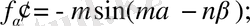
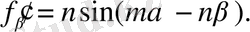
Шешуі. 1) Дифференциалдаудың ережесіне сәйкес тұрақты айнымалыны табамыз: 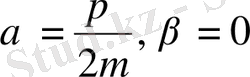, осыдан 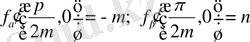аламыз.
2) Айнымалыны тауып, одан тұрақты мәнді тауып, оған бағытталған нүктені табамыз: .
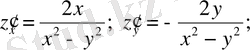
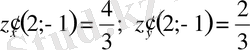Мысал 2. 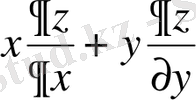қанағаттандыратын 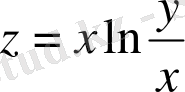функцияның дербес туындыларын табыңыз.
Шешуі. Функция құрып ондағы тұрақты айнымалылар х және у табыңыз:
; ;
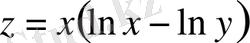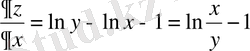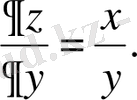
қою арқылы 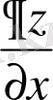және 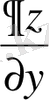есепті шеше аламыз, осыдан 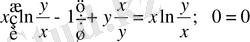. Яғни бұл формула жүйесін нақтылайды (оның кеңейтілуі болып табылады).3

7.4 Көп айнымалы функциялардың дифференциалдары

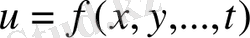функциясының 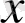бойынша дербес дифференциалы деп 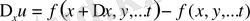дербес өсімшесіне сәйкес келетін байланысты басты бөлігін айтамыз.
Аналогиялық түрде функциясының басқа аргументтерінен дербес дифференциалдарын алуға болады.
функциясынан 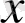бойынша, 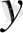,..., 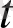бойынша сәйкес 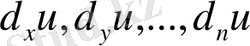дербес дифференциалдары белгіленеді.
Дербес туындының анықтамасынан:
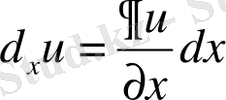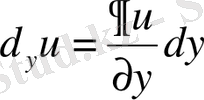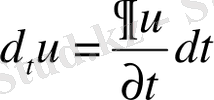;;...; . (1.4.1)
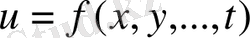функциясының толық дифференциалы деп 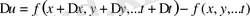оның толық өсімшесінің 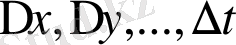байланысты өсімшесі (немесе 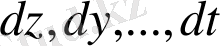дифференциалдары) басты бөлігін айтамыз.
du функциясының толық дифференциалы және 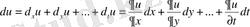оның барлық дербес дифференциалдарының қосындыларына тең.
Егер 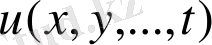нүктелерінде толық дифференциалы болса, функция 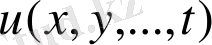нүктелерінде дифференциалданады деп аталады.
Мысал 1: Функцияның толық дифференциалын табыңыз:
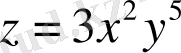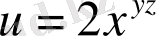1) ; 2) ; 3) .
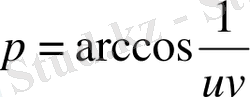Шешуі. 1) а. Функцияның дербес туындысын табамыз: ; .
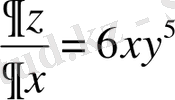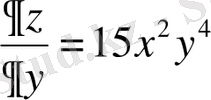б. Дербес дифференциалдарды сәйкес аргументтеріне көбейтіп, дербес дифференциалдарды аламыз: ; .
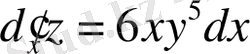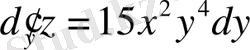в. Функцияның толық дифференциалы оның дербес дифференциалдарының қосындысы арқылы табамыз:
.
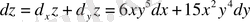2) Осы жоспарға сүйене отырып, былай табуға болады:
а. ; ; ;
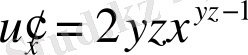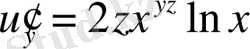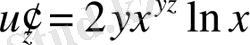б. ; ; ;
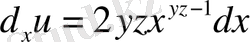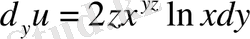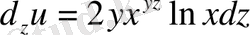в. .
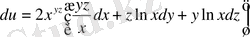3) а. ; ;
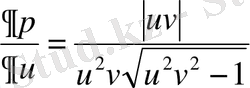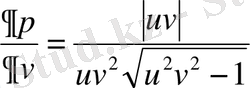б.; ;
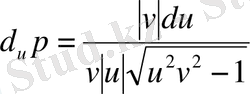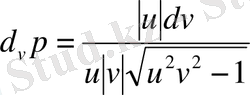в. .
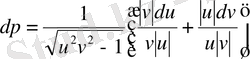Мысал 2: Толық дифференциалды табыңыз:
.
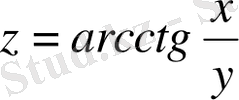
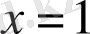
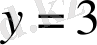
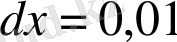
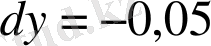Шешуі. ; ; .
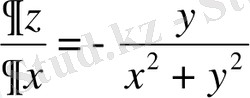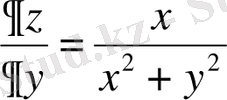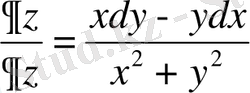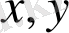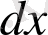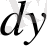Бұл жерде белгісіз мәндері қойылады және функцияларындағы 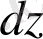толық дифференциалды аламыз:
.4

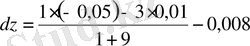1.5 Күделі функцияның дифференциалы

Егер функция 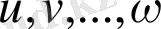, 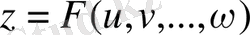аралық аргументтер арқылы берілсе, 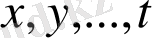тәуелсіз айнымалыларынан алынған 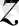айнымалысы күрделі функция деп аталады. Мұндағы ,,...,.
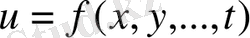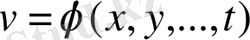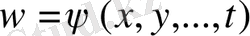Бір тәуелсіз айнымалысы бойынша алынған күрделі функцияның дербес туындысы оның аралық аргументтерінен алынған дербес туындыларының бұл аргументтерінің тәуелсіз айнымалы дербес туындыланының қосындысын айтамыз:
;
;
... ... ... ... ... ... ... ... ... ... ... ...
.
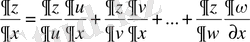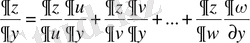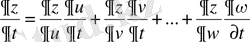Барлық 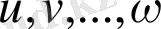аргументтері x тәуелсіз айнымалы бойынша функция болса, онда z функциясы x бойынша алынған күрделі функция деп аталады. Күрделі функцияның туындысы төмендегі формуламен анықталады:
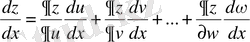(1.5.1)
Мысал 1: Күрделі функцияның туындысын есептеңіз:
1) , , ;
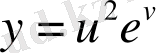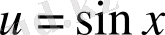2) , , ;
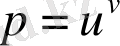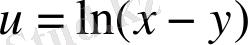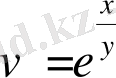3) , , .
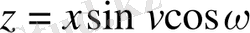Шешуі. 1) Бұл жерде функция х-тен алынған у күрделі функциясы жоғарыдағы формуланы пайдалана отыра, мынаны аламыз:

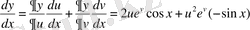
2) p функциясы x және y айнымалыларынан алынған күрделі функция, формуланы пайдаланып:

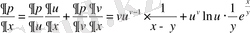
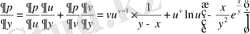
3) х айнымалысынан алынған z күрделі функциясы берілген: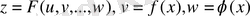. Функцияның толық дифференциалының формуласынан (u=x болғанда) (**) аламыз:
.
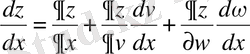Осы формулаға сәйкес:
5

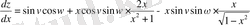
1.6 Бетке түсірілген жанама жазықтық және нормаль

Бет 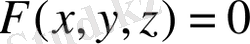теңдеуімен берілген болса және 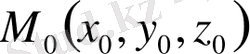нүктесі осы бетте жататын болса, онда:
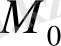нүктесінде бетке түсірілген жанама төмендегі теңдеумен анықталады:
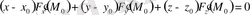(1.6.1)
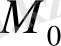нүктесінде бетке түсірілген нормаль ( 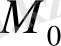нүктесі арқылы өтетін және жанама жазықтығына перпендикуляр болатын түзу) анықталған теңдеу:
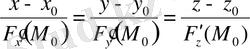(1.6.2)
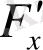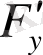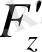,, дербес бірінші ретті туындылары бір мезетте 0-ге тең болатын 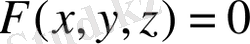бетінің нүктелері ерекше нүктелері деп аталады. Бұл нүктелерде беттің жанама жақықтығы және нормалі болмайды.
Мысал 1: 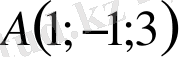нүктесінде 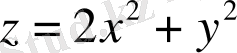эллипстік параболоидқа жүргізілген жанама және нормаль теңдеуін табыңыз.
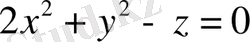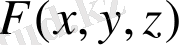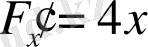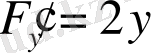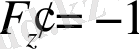
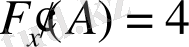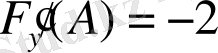
Шешуі. Теңдеуді түрлендіру арқылы бет мына түрге келтірілді. Оның сол жағын деп белгілеп, одан , , , 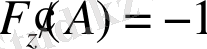қойып, ортақ ережеге сәйкес (І), (ІІ) формулаларға есептейміз: 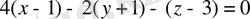немесе 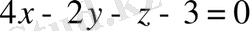. Ал жалпы жағдайда ол:

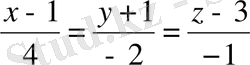
Мысал 2: Кеңістікте 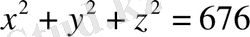сфераға сәйкес нүктеде 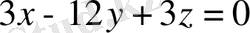жазықтықтағы жанамаға параллель жазықтық болады.
Шешуі. (І) формуланы қолдана отырып, мынадай жазықтықтағы жанаманы кеңістіктегі 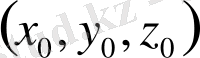нүкте арқылы құрастырамыз.
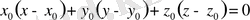немесе .
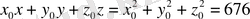Екі жазықтықтың паралельдігі бойынша, яғни жазықтықтағы жанама жазықтыққа параллель, теңдеудегі коэффициенттер бір-біріне пропорциональ болады: .
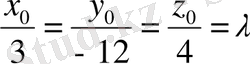Мұндағы анықталған 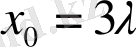, , 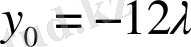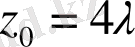және сфераның теңдеуіне қойсақ: 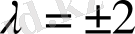және сферада табылған 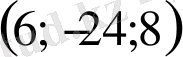және нүктелер арқылы жазықтықтағы жанамаға параллель жанама болады.6

1.7 Көп айнымалы функцияның экстремумы. Функцияның ең үлкен және ең кіші мәні

Егер 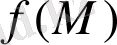функцияның мәні оған жақын нүктелермен салыстырғанда ең үлкен (ең кіші) болса, онда 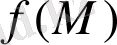функцияның 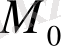нүктедегі мәні максимумы (минимумы) деп аталады.
Көп айнымалы функцияның анықталу облысында жататын нүктелерде функцияның барлық бірінші ретті дербес туындылары нөлге тең немесе мүлдем болмаса функция максимумы немесе минимумы (экстремумдары)болады. Бұл нүктелерді кризистік нүктелер деп атайды.
Егер барлық М нүктесі үшін 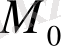нүктесіне жақын ( 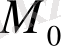аймағында) 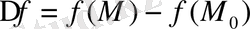функция өсімшесінің таңбасы өзгермесе, 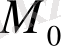кризистік нүктелері 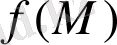функцияның экстремум нүктесі болады.
Егер 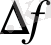оң таңбаны сақтаса, онда 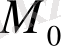минимум нүктесі болады, егер де 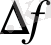теріс таңбаны сақтаса, 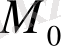нүкте функцияның максимумы болады.
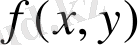екі айнымалы функция мен 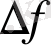таңбасы зерртеу үшін әрбір 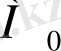критикалық нүктесін зерттеу мүмкін, функция екі рет дифференциалданып, анықтауыш бойынша анықталады:
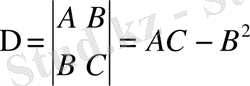(1.7.1)
немесе
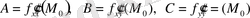(1.7.2)
Мұндағы:
1) егер , 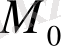экстремум нүктесі болады: 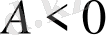(немесе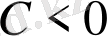) максимум нүктесі, ал 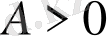( немесе) минимум нүкте;
2) егер 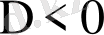, онда 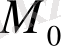экстрмум нүктесі болмайды;
3) егер 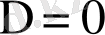, онда нақты шешім туралы немесе 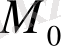нүктеде экстремум болмайтынын әрі қарай зерттеу талап етіледі. Мысалы, 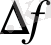өсімшесінің белгі бойынша осы нүктеге жақындауы.
1) және 2) шарттардың бар болуы немесе болмауы экстремумды зерттеуге жеткілікті.
Бір айнымалы функцияда сияқты көп айнымалы функцияның ең үлкен немесе ең кіші мәндері бірдей анықталады.
Ең үлкен және ең кіші функцияның барлық мәнін максимум немесе минимум салыстыруға болмайды, себебі ең үлкен және ең кіші функциянын мәнін нүкте маңайының мәніне сәйкес келеді.
Егер функция тұйықталған облыста үзіліссіз немесе үзілісті болса, онда ол бірде ең үлкен, бірде ең кіші мәні болмауы да мүмкін.
Кейде D тұйықталған облыспен шектелген үзіліссіз болса, онда 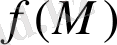функциясының ең үлкен немесе ең кіші мәні міндетті түрде осы облыста болады. D облысының ішінде немесе шекарасында жатса, онда оған жету мәні немесе экстремум нүкте болады.
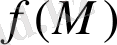функциясы D тұйықталған облыста ең үлкен ( ең кіші) мәнін, үзіліссіз, келесі ереже бойынша табылады:
А. D облысының ішінде жататын және осы нүктедегі функцияның мәнін есептеп, критикалық нүктені табыңыз.
Б. D облысының шекарасындағы функцияның ең үлкен (ең кіші) мәнін табыңыз.
В. Барлық D облысындағы функцияның ең үлкен (ең кіші) мәнімен шыққан функцияның ең үлкен (ең кіші) мәнін салыстырыңыз.
Мысал 1: Функцияның экстремумын табыңыз:
1) ;
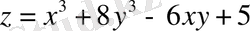2) ;
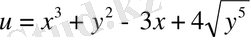3) ;
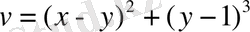4) .
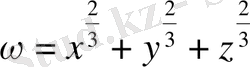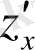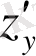Шешуі. 1) және бірінші ретті дербес туындыны және критикалық нүктені, яғни 0-ге тең немесе жоқ болу және функцияның ішкі анықталу облысында табамыз: 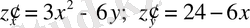. 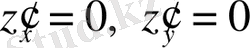теңдеулер жүйесін шешеміз, 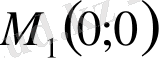және 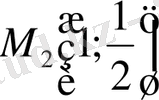екі нүктені табамыз. Критикалық екі нүктенің бар болуы, осылай функциясы барлық 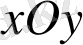жазықтығында анықталады. Басқа критикалық нүкте жоқ, осылай кез келген немесе мәніне 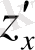немесе 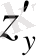сәйкес келеді.
анықтауыштың таңбасына қарап 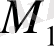немесе 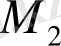критикалық нүктені зерттейміз, екінші ретті дербес туындыны құрамыз: ; ; .
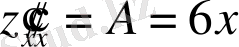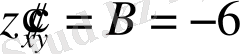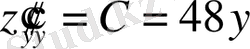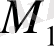нүктесі арқылы 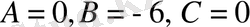немесе 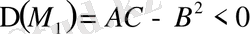аламыз. Сондықтан 2) жеткілікті шарт бойынша 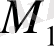нүктесінде экстремумы жоқ.
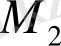нүктесі арқылы 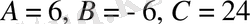немесе 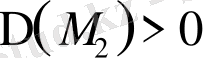аламыз. 1) жеткілікті шарт бойынша 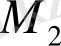нүктесі минимум болады.
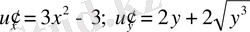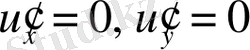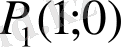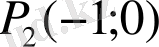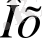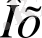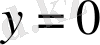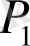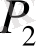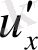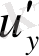2) критикалық нүктені іздейміз. теңдеулер жүйесінен және нүктелерді табамыз. Бұл нүктелер функцияның анықталу облысында жатады( жартылай жазықтықта, осіне жоғары жағы, енгізілген немесе осі), бірақ бұлар аймақтың сыртында орналасқан, ал шекарасы:. Сондықтан және критикалық нүкте болып табылмайды. функциясының барлық анықталу облысында және бірінші ретті туынды бар болады. Сондықтан бұл функцияны не критикалық, не экстремумы таба алмаймыз.
3) 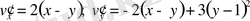критикалық нүктені іздейміз.
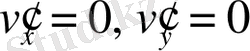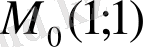теңдеулер жүйесін шешіп, функияның жалғыз критикалық нүктені аламыз.
экстремум нүктесін қою үшін, біз мәнін есептейміз:
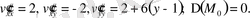
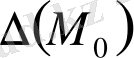таңбасына қарамаймыз (3 жағдай). 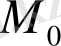критикалық нүктесін функцияның экстремумына қояйық, 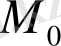нүктенің маңайына жақын таңбаны есептейміз: .
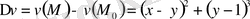М нүктесі 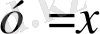биссектрисасында жатсын. Онда 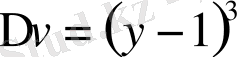. Егер 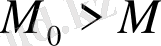, егер 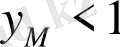болса, онда 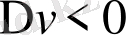, ал егер 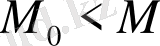, егер 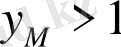болса, онда 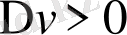болады. 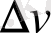айырымы 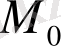нүктесіне жақындағанда таңбасы сақталмайды, сондықтан 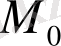нүктесінде экстремумы жоқ.
4) Критикалық нүктесін іздейміз: . Мына дербес туынды 0-де, мұндағы ешқайсысы мәндеріне назар аударылмайды, олар нүктеде болмайды ( шексіздікте назар аударылады). нүкте функцияның анықталу облысында жатады. кеңістіктегі барлық нүктелер жиынтығын көрсетеді. Сондықтан критикалық нүкте. нүктеге жақын айырма таңбасын зерттеуге көз жеткізіп, мұндағы мәндері 0-ден басқа, ол оң таңбасын сақтайды. Сондықтан минимум нүкте болады. 7
Мысал 2: Функцияның ең үлкен және ең кіші мәні есептеңіз:
1) дөңгелекте ;
2) немесе түзулермен тұйықталған аймақта .
Шешуі. 1) Ережеге сәйкес:
А. функциясының критикалық нүктесін табайық, дөңгелектің ішінде жататын және оның мәнін мына нүктелер арқылы есеп есептейік: ; теңдеулер жүйесін шешейік, дөңгелектің ішінде жатқан критикалық нүктесін шығады. бұл нүктедегі функцияның мәні.
Б. шеңберіндегі функцияның ең үлкен (ең кіші) мәнін табайық. және айнымалылары шеңбердің теңдеуімен өзара байланысы. Осы теңдеуден бір айнымалыны басқа айнымалы арқылы өрнектеп алайық, мысалы,, және функциясына өрнекті алып барып қояйық, солай функция бір айнымалы болып шығады:. өзгеру аралығы .
дөңгелекпен шектелген функцияның ең үлкен және ең кіші мәні, аралықта анықталған функциясының ең үлкен және ең кіші мәніне сәйкес келеді.
І. функциясының критикалық нүктесін табайық, аралықта жататын және оны мына нүктелерде есептейік: ; , нүктеде. мына нүктеде мәні.
ІІ. соңғы аралықта мәнін есептейік: .
ІІІ. ішкі критикалық нүктесі және соңғы және аралықтағы қорытындыны мәнімен салыстырайық: аралықтағы функциясының ең үлкен мәні ( функциясы шекарасы - шеңберді ) -ге тең. Ал функциясының ең кіші мәні берілген аралыққа -ге тең.
В. Шеңбердің ең үлкен және ең кіші мәнін критикалық нүктедегі мәнінмен салыстырып қорытайық: тұйықталған облыс- дөңгелекте функциясының ең үлкен мәні -ға тең және және шекаралық нүкте, облысқа тең және және шекаралық нүктеге жақынды ең кіші мәні болып табылады. ,,, шеңберде жататын ордината нүктелері, шеңбердің теңдеуі арқылы абсцисса есептелді.
2) Ережеге сәйкес:
А. Берілген аймақта жататын функциясының критикалық нүктесін іздейік: ; . , теңдеулер жүйесін шығарайық, және екі критикалық нүктені табайық, берілген аймақтың ішінде бірде біреуі жатпайтын. функциясының басқа критикалық нүктесі болмайды.
Б. Берілген аймақтың шекарасында ең үлкен және ең кіші мәнін табайық. Ол екі участков негізінде АОВ және АВ әртүрлі теңдеуден тұрады. Сондықтан ең алдымен әр участковтың ең үлкен және ең кіші мәнін табайық, содан кейін оларды салыстырып, барлық шекарасында ең үлкен және ең кіші мәнін табайық.
АОВ участкесінде болу, , өзгеру аралығы .
аралығында ең үлкен және ең кіші мәнін табайық:
І. егер ;.
ІІ. .
ІІІ. іш жағынан критикалық нүктені және соңғы аралықтағы мәнін салыстырып қорытайық: аралығында -дің ең үдкен мәні 32 тең ( нүкте), ал ең кіші мәні 0 -ге тең аралық ( нүктеде).
АВ аймағын , табамыз. Мұнда .
аралықта -нің ең үлкен және ең кіші мәнін табамыз:
І. ; берілген аралықтың ішінде, мұндағы ( С нүктеде):.
ІІ.
ІІІ. ең үлкен мәні кесіндіде 32 - ге тең ( нүктесінде), ал ең кіші мәнінде осы кесіндіде тең ( нүктеде).
-нің АОВ және АВ аймағындағы мәнін салыстырып қорытындыға келеміз. АОВА аймағының барлық шектерінде функцияның ең үлккен мәні 32-ге тең. Ал оның ең кіші мәні 0-ге тең.
В. функция берілген тұйықталған аймақтың ішінде экстремумге ие емес , оның осы нүктеде бұл аймақтың ішінде жататын ең үлкен және ең кіші мәндері жеткілікті. және шеткі нүктелерінде ең үлкен мәнге ие,, ал шеткі нүктеде ол ең кіші мәнге ие.8

1. Maple 7 жүйесінің мүмкіндіктері

2.1 Maple 7 жүйесінде үш өлшемді графиктерді салу мүмкіндіктері

Maple жүйесінде математикалық графиканың көптеген түрлерін іске асыруға болады. Мұнда Декарт координаттар жүйесі немесе поляр координаттар жүйесінде тұрғызылатын қарапайым функцияларының графиктерінен бастап ең күрделі, әртүрлі фигуралардың қиылысуы нәтижесінен келіп шығатын графиктерді сызуға болады.Сонымен бірге әр түрлі теңдеулер шешімінің графигі сызылып көрсетіледі.
Maple жүйесінде бірнеше функциялардың графиктерін сызу мүмкіндігі бар. Мұндай жағдайда графиктерді бір-бірінен ажыратып көрсету үшін оларды әр түрлі стилде сызуға болады. Бұл мүмкіншіліктен мысалы графиктерді экранға немесе қағазға шығарғанда пайдалануға болады.
Көп айнымалы функциялардың графигін бір координата жүйесінде шығару мысалы қарастырылады. Мұндай графиктарды сызу үшін бұл функциялардың аттары жазылып, олардың аргументтерінің өзгеру облысы көрсетіледі.
Көп айнымалы функциялардың тұрғызған кезде ол функция plot бұйрығында f тың орнында анық көріністе жазылу керек.
Үш айнымалы функциялардың графикасының өзгеше жері plot3d функциясы қолданылады. Мұндай графиктердің әрбір zi нуктелері XY жазықтықта жататын, (х,у) координаттарымен берілетін нүкте биіктігі (аппликатасы) болады. Компьютер экраны бірінші жуықтауда жазықты болғандықтан практикада үш өлшемді графика объектілерінің арнайы проекциясын көрсетеді.
Үш айнымалы функциялардың графигін сызу үшін plot3d бұйрығы қолданылады.
Математикада y(x) функциялық байланыстар көп қолданылады. Бұл байланыстардың графиктері жазықтықтағы y1 (x1) нүктелер тізбектерін тұтастыру нәтижесінде сызылады. Демек график сызу үшін сызықты интерполяция пайдаланылады. Егер нүктелер саны жетерлі дәрежеде көп болса, онда график жуықтап сызылғаны білінбейді. Екі айнымалы функциялардың графиктерін сызу үшін plot функциясы пайдаланылады. Бұл функция
plot(f, х. v) plot(f. х. v. о)
көріністерде қолданылады. Бұл жерде f -- графигі сызылатын функция, х -- айнымалының аты, v -- функция мәні жататын аймақ (оны көрсету шарт емес), о -- график стилін анықтайтын бір немесе бірнеше параметрлер (сызық қалындығы, оның түсін тағыда басқа параметрлер). 10
Функция графигін сызған кезде сызықтың өзін сызудан басқа графиктың кейбір қасиеттерінде анықтау керек болады. Мысалы үшін: осьтардың координаттарын , сызық типі және түсі т.б. Бұл үшін графика параметрлерін қолдану керек болады. Maple жүйесінде екі қатпарлыы пластинкалардың графикасын үшін төмендегі кейбір параметрлерді қолдануға болады:
axes -- әр түрлі координаттар типтерін шығару (axes=NORMAL -- кәдімгі қарапайым осьтар, axes=BOXES -- график рамка ішінде шығады, axes=FRAME -- осьтар қиылысқан сызықтар көріністе болады, axes=NONE -- осьтер көрінбейді );
axes font -- координаттарды бөліп шығару жазуын белгілеу;
color -- сызық түсін таңдау;
coords -- координаттар системасы типін белгілеу;
discont -үзіліссіз график (задает построение непрерывного графика ) (значения true или false);
font -- шрифт таңдау;
labels -- координаттарды ось бойынша [X, Y] көріністегі жазу шығару;
size. -- шрифт өлшемін белгілеу;
style -- графикты құру стилін таңдау (POINT -- нүктелі, LINE -- сызық пен);
title -- график басына сөз жазу (title="string", string -- мәтін);
Maple жүйесінде бірнеше функциялардың графиктерін сызу мүмкіндігі бар. Мұндай жағдайда графиктерді бір-бірінен ажыратып көрсету үшін оларды әр түрлі стилде сызу мүмкін. Бұл мүмкіншіліктен мысалы графиктерді экранға немесе қағазға шығарғанда пайдалануға болады. Егер графикті сызған кезде style параметрін пайдалансақ, онда сызықтың түрлерін style параметрінің төмендегі:
POINT немесе point -- график нүктемен шығарылады;
LINE немесе line -- график тұтас сызықпен шығарылады.
Сolor атты параметр жәрдемінде график сызықтарының әртүрлі түстерін таңдауға болады.
Мысалы үшін:
1
aquamarine
black
blue
navy
coral
2
cyan
Brown
gold
green
gray
3
grey
khaki
magenta
maroon
orange
4
pink
plum
red
sienna
tan
5
turquoise
violet
wheat
white
yellow
Бір қатпарлы пластинкалардың графигін тұрғызған кезде ол функция plot бұйрығында f тың орнында анық көріністе жазылу керек. Мысалы үшін:
Үш айнымалы функциялардың графикасының өзгеше жері plot3d функциясын қолдануда. Мұндай графиктердің әрбір zi нүктелері XY жазықтықта жататын, (х,у) координаттарымен берілетін нүкте биіктігі (аппликатасы) болады. Компьютер экраны бірінші жуықтауда жазықты болғандықтан практикада үш өлшемді графика көлемді объекттердің арнайы проекциясы болады.
Үш айнымалы функциялардың графигін сызу үшін plot3d бұйрығы қолданылады. Бұл бұйрық:
p1ot3d(exprl. x=a..b. y=c..d,p)
plot3d(f, a..b. c..d.p)
plot3d([exprf.exprg.exprh]. s=a..b, t=c..d.p)
plot3d([f.g.h]. a..b, c..d,p)
форматтардың біреуінде қолданылуы мүмкін .Бұл формалардың бірінші екеуі әдетте бір беттің графигін сызуға қолданылады, ал қалғандары параметрлік формада берілген беттердің графигін сызады. Жоғарыда келтірілген формаларда f, g және h тар -- функциялар , exprl- х және у байланысты өрнек ; exprf, exprg және exprh - беттерді параметрлі анықтайтын өрнектер, а және b нақты түрдегі сандық тұрақтылар, х, у, s және t лар тәуелсіз айнымалдар, р-басқарушы параметр болып есептеледі.
Рlot3d бұйрығының параметрлері. Р- параметр жәрдемінде кең аралықта үш өлшемді графикада беттердің түсін, олардың көріну бұрыштарын ауыстыру, координат осьтерінің көрінісін ауыстыру т.б. басқаруға болады.
Р1ot3d параметрлері plot бұйрықтың параметрлері сияқты қолданылады:
Бірақ plot3d бұйрығының арнайы параметрлері де бар: Мысалы үшін
ambientl light=[r,g,b] -- (r)-қызыл, (g)-жасыл және (b)-көк түстерді таңдайды;
axes=f -- координаттар осьтерінің көрінісін таңдайды (BOXED, NORMAL, FRAME және NONE);
grid=[m,n] -- бет каркасы сызықтарын таңдайды;
gridstyle=x -- x - каркас сызықтары стилін таңдайды ('rectangular' немесе 'triangular');
1abels=[x,y,z] -- осьтар бойынша жазу шығарады (х, у және z -- ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.