Эллипстикалық теңдеулер және гармониялық функциялар: Лаплас теңдеуі, шеттік есептер және шешу әдістері


Мазмұны.
Кіріспе.
Эллипстикалық теңдеулер типі.
I . Лаплас теңдеуіне әкелетін есептер.
1. 1 Стационарлық жылулық өріс.
Шеттік есептерді қойылуы . . . 6
1. 2 Сұйықтың потенциал ағысы.
Стационар тоғының және электростатикалық өрістің потенциалы . . . 7
1. 3 Қисықсызықты координаттар жүйесіндегі
Лаплас теңдеуі . . . 9
1. 4 Лаплас теңдеуінің кейбір дербес шешімдері . . . 14
1. 5 Комплекс айнымалысының гармониялық және аналитикалық функциясы . . . 15
1. 6 Кері радиус - векторларды түрлендіру . . . 18
II. Гармониялық функцяның жалпы есептері.
2 . 1 Грин формулалары.
Шешімнің интегралды көрінісі . . . 20
2. 2 Гармониялық функцияның кейбір негізгі шешімдері…27
2. 3 Бірінші шеттік есептің тұрақтылығы
және жалғыздығы . . . 31
2. 4 Үзілісті шекаралық шарттары бар есептер . . . 32
2. 5 Оқшауланған ерекше нүктелер . . . 33
2. 6 Шексіздіктегі үш айнымалысы бар гармониялық функцияның реттілігі . . . 36
2. 7 Ішкі шеттік есептер.
Екі- және үшөлшемді есептер үшін шешімнің жалғыздығы . . . 38
2. 8 Екінші шеттік есеп.
Жалғыздық теоремасы . . . 41
III. Қарапайым облыстар үшін шеттік есептерді
айнымалыларды ажырату әдісімен шешу.
3. 1 Дөңгелек үшін бірінші шеттік есеп . . . 45
3. 2 Пуассон интегралы . . . 51
3. 3 Үзілісті шераралық мағына жағдайы . . . 55
IV. Потенциалдар теориясы.
4. 1 Көлемді потенциал . . . 58
4. 2 Жазық есеп . . . 60
4. 3 Меншіксіз интегралдар . . . 62
4. 4 Беттік потенциалдар . . . 69
Қорытынды . . . …75
Қолданылған әдебиеттер . . …. . …85
Кіріспе.
Бұл дипломдық жұмыста эллипстикалық типтегі теңдеулерді шешудің әдістері қарастырылады
Жылуды, дыбысты, жарықты электротоқты сипаттау шамасы уақытқа тәуелді болса, онда оларды орнықсыз динамикалық процестер деп атайды.
Сонымен бірге динамикалық процестердің сипаттау шамасы уақытқа тәуелді болмауы да мүмкін. Бұл жағдайда ол - орықты қозғалыс болып табылады.
Мысалы, кейбір қозғалмайтын ось бойымен бірқалыпты айналып тұрған, қатты тұйық ыдыс ішінде сығылмаған сұйық бар деп ұйғарайық. Ыдысты толтырған сұйық, уақыттан тәуелсіз, тек х, у, z координатталардан тәуелді жылдамдық потенциалымен қозғалады. Сұйық массасындағы қарастырылып отырған орнықты ағысты аламыз.
U анықтамасы келесі теңдеуді интегралдау жолына әкеледі.
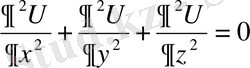 (1)
(1)
Осы теңдеуді U ыдыс ішіндегі барлық нүктелерде қанағаттандыру керек (және егер уақыттан тәуелсіз болса, ол мына (0) формуласынан пайда болады) . Осыдан бастапқы шарт көңілсіз қалады да, бірақ шектік шарт бұрынғышы орындалуы керек. Ыдыстың қабырғасына жанасқан, сұйықтың кез келген бөлшегінің нормаль құрушы жылдамдағы қатты ыдыс нүктесінің нормаль құрушы жалдымдығына тең болады. Осы жағдайда координат осіндегі сұйық нүктесінің жылдамдығының u, v, w проекциясы мынадай
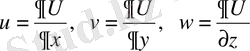
болса, онда х, у, z мағыналары үшін ыдыстың бетіндегі х, у, z нүктелеріндегі сұйықтың бөлшегінің нормаль құрушысы мына өрнектің мағынасына тең болады.
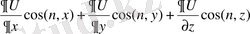
Координаталары сондай мағыналарға ие, ыдыс қабырғасындағы нүктенің нормаль құрушы жылдамдығы белгіді, өйткені ыдыстың қозғалысы берілген болатын, яғни оның бетіндегі нүктелерінің координаталары f=(х, у, z) функциясымен берілген.
Сұйықты шектейтін, беттегі барлық нүктелерінде шеттік (беттік) шартты қанағаттандыратын
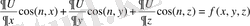
U теңдеуінің шешімін табатын есепке әкелінеді.
Бұл есеп гидродинамикада негізгі болып табылады және Карл Нейман есебі деп аталынады.
Осындай анализ есептеріне физиканың статистикалық есептері келтіріледі, мысалы, дененің теңдес жылуы туралы есеп, Ньютонның заңы бойынша тартылыс теория есептері және т. с. с.
Берілген беттегі контурда электр теңдесінің есебі, электрлік массалардың U потенциалының анықтамасына әкеледі. Контур бетіндегі үлестіру дегеніміз - контур бетінен тыс және ішінде U келесі шартты қанағаттандырып,
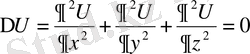 (2)
(2)
кеңістіктің шексіз алыстатылған нүктесі үшін нөлге айналып кететін және контур бетіндегі кез келген нүктесіне сыртқы жағынан х, у, z нүктесінің жақындау барысында тұрақты шамаға ұмтылады. (9) формуласын Лаплас теңдеуі деп атайды.
Егер контур бетіндегі нүктесінің U шектік мағынаны U е арқылы белгілейік, сонда (9) шарты келесі түрде болады.
U
е
 (3)
(3)
мұндағы
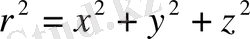 .
.
Есеп (10) түрдегі шектік шартты қанағаттандыратын (2) теңдеуінің шешімінің ануқтамасына тағыда әкеледі.
Бұл есепте математикалық физикада және анализда аса маңызды Дирихле сыртқы есебінің дербес жағдайын көріп тұрмыз.
Жалпы бұл есеп екіге бөлінеді: ішкі және сыртқы болып.
Біріншісінде берілген тұйық беттің ішінде жатқан
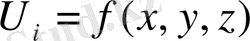
шектік шартты қанағаттандыратын барлық нүктелер үшін Лаплас теңдеуінің шешімін табу талап етіледі. Мұндағы
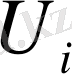 -
U
функциясы ұмтылған шек, ал
-
U
функциясы ұмтылған шек, ал
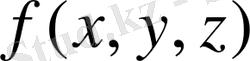 - осы беттегі нүктелердің берілген функциясын білдіреді.
- осы беттегі нүктелердің берілген функциясын білдіреді.
Сыртқы есепте
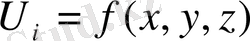

шектік шарт шарты болғандағы, кейбір тұйық бетке арақатынасты, сырттай барлық нүктелерде Лаплас теңдеуін қанағаттандыратын U функциясын анықтау талап етіледі.
Диплом бес бөлімнен тұрады. Әр бөлімде өзіне сәйкес тақырыпшалары мен сәйкес есептері бар. Енді соларды қарастыруға көшейік.
1. Эллипстикалық теңдеулер типі.
Әр түрлі физикалық табиғаттың ( диффузия, тербеліс, жылуөткізгіштік және т. б. ) стацоинарлық процестерін зерттеу барысы эллипстикалық теңдеулер типіне әкеледі. Осы типтің ең көп тараған теңдеуі - Лаплас теңдеуі болып табылады.
∆u = 0
анықтама :
Егер
 облысында функция 2-ші ретті туындыларымен бірге үзіліссіз және Лаплас теңдеуін қанағаттандыратын болса, онда
u
функциясы гармоникалық болады .
облысында функция 2-ші ретті туындыларымен бірге үзіліссіз және Лаплас теңдеуін қанағаттандыратын болса, онда
u
функциясы гармоникалық болады .
1. Лаплас теңдеуіне әкелетін есептер.
1. 1 Стационарлық жылулық өріс. Шеттік есептің қойылуы.
Стационарлық жылулық есепті қарастырайық.
∆u = 0 (1)
Стационарлық емес жылулық өрістің температурасы жылуөткізгіштік дифференциалдық теңдеуді қанағаттандырады
u
t
= a
2
∆u (a
2
=
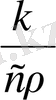 )
)
Егер процесс стационарлық болса, онда Лаплса теңдеуін қанағаттандыратын және уақытқа байланыссыз температураның u(x, y, z) үлестіруі орнатылады.
Жылудың шығар жері бар болғандықтан мынадай теңдеу аламыз.
∆u =-ƒ, ƒ=
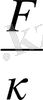 , (2)
, (2)
Мұндағы F - жылу көзінің тығыздығы, κ- жылуөткізгіштіктің коэффиценті.
Біртектілі емес Лаплас теңдеуінің (2) кейде Пуассон теңдеуі деп те атайды.
 - бетімен шектелген, кейбір
- бетімен шектелген, кейбір
 көлемін қарастырайық.
көлемін қарастырайық.
 дененің ішінде температураның
u(x, y, z)
стационарлық таралу есебі келесідей тұжырымдалады:
дененің ішінде температураның
u(x, y, z)
стационарлық таралу есебі келесідей тұжырымдалады:
 ішіндегі
ішіндегі
∆u = -f(x, y, z)
теңдеуін және шекаралық шартты қанағаттандыратын функцияны u(x, y, z) табу керек.
Шекаралық шарт келесі түрдегідей бола алады.
I.
U=f
1
 - ға байланысты (бірінші шеттік есеп)
- ға байланысты (бірінші шеттік есеп)
II.
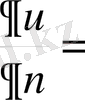 f
2
f
2
 - ға байланысты (екінші шеттік есеп)
- ға байланысты (екінші шеттік есеп)
III.
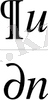 +h(u - f
3
) =0
+h(u - f
3
) =0
 - ға байланысты (үшінші шеттік есеп)
- ға байланысты (үшінші шеттік есеп)
Мұндағы f
1
, f
2
, f
3
, h - берілген функциялар
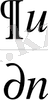 - Σ бетіне сырттай нормаль туындысы.
- Σ бетіне сырттай нормаль туындысы.
Лаплас теңдеуі үшін бірінші шеттік есепті Дирихле есебі деп, ал екінші шеттік есепті - Нейман есебі деп атайды.
Егер
 0
облысында
0
облысында
 бетіне қатысты сыртқы шешімі табылатын болса, онда осы есепті сыртқы шектік есеп деп атайды. Егер
бетіне қатысты сыртқы шешімі табылатын болса, онда осы есепті сыртқы шектік есеп деп атайды. Егер
 0
облысында
0
облысында
 бетіне қатысты ішкі шешімі табылатын болса, онда осы есепті ішкі шектік есеп деп атайды.
бетіне қатысты ішкі шешімі табылатын болса, онда осы есепті ішкі шектік есеп деп атайды.
1. 2 Сұйықтың потенциал ағысы. Стационар тоғының және электростатикалық өрістің потенциалы.
Қайнар көзсіз сұйықтын потенциал ағысына мысал келтірейік. υ(x, y, z)
жылдамдығымен сипатталған стационарлық сұйық ағысы орын алады. Егер сұйық ағысы құйынсыз болса, онда жылдамдық υ потенциалдық вектор болып табылады, яғни
υ= - grad φ (3)
мұндағы - φ жылдамдық потенциалы деп аталатын скалярлық функция.
Егер сұйық көзі болмаса, онда
div υ= 0 (4)
(3) - өрнегін υ (4) -ке қоятын болсақ:
div grad φ=0
немесе
Δφ=0 (5)
яғни жылдамдық потенциалы Лаплас теңдеуін қанағаттандырады.
Біртекті өткізгіш ортада тығыздығы j(x, y, z) көлемі бар стационарлық ток болсын. Егер ортада көлемді ток көздері болмаса, онда
div j= 0 (6)
Элекрт өрісі
 Ом заңының дифференциалынан ток тығыздығы арқылы анықталады
Ом заңының дифференциалынан ток тығыздығы арқылы анықталады
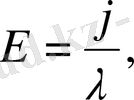 (7)
(7)
Мұндағы λ - орта өткізгіштігі. Процесс стационарлық болғандықтан, электр өрісі құйынсыз, немесе потенциалды болып келеді1, яғни скаляр функция ϕ(x, y, z) бар болады, онда
E= -grad ϕ (
 = - λgrad ϕ)
(8)
= - λgrad ϕ)
(8)
- және (7) формулалары арқылы қорытынды жасасақ,
Δφ =0 (9)
Басқаша айтқанда, электр өрісі және стационарлық тоғының потенциалы Лаплас теңдеуін қанағаттандырады.
Стационарлық зарядтан тұратын электр өрісін қарастырайық. Процестің стационарлығынан шығатыны
 (10)
(10)
яғни өріс потенциалды және
E= - grad φ (8)
ε = 1 диэлектрлі тұрақтымен сипатталған ортада
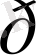 (x, y, z)
тығыздығы көлемді зарядтар болсын. Электродинамиканың негізгі заңына сүйенсек
(x, y, z)
тығыздығы көлемді зарядтар болсын. Электродинамиканың негізгі заңына сүйенсек
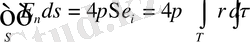 (11)
(11)
мұндағы
 - кейбір көлем, S - оны шектеп тұрған бет,
- кейбір көлем, S - оны шектеп тұрған бет,

 -
-
 ішіндегі барлық зарядтардың қосындысы және Остроградскийдің теоремасын
ішіндегі барлық зарядтардың қосындысы және Остроградскийдің теоремасын
қолдансақ
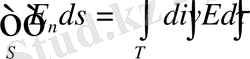 (12)
(12)
онда
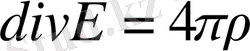 аламыз
аламыз
 үшін (8) өрнекті қоятын болсақ, онда
үшін (8) өрнекті қоятын болсақ, онда
Δφ= -4πρ (13)
яғни электростатикалық потенциал Пуассон теңдеуін қанағаттандырады.
Егер көлемді зарядтар болмаса (ρ=0) , онда потенциал Лаплас теңдеуін қанағаттандыруы қажет.
Δφ =0
Негізгі шеттік есептер қарастырылған процестер үшін жоғарыда көрсетілген үш типке қатысты.
1. 3 Қисықсызықты координаттар жүйесіндегі Лаплас теңдеуі.
Ортогональ қисықсызықты координаттар жүйесінде Лаплас теңдеуін қарастырайық. Кеңістікте Декарт координаталарының x, y, z орнына
q 1 = f 1 (x, y, z) , q 2 = f 2 (x, y, z) , q 3 = f 3 (x, y, z ) (14)
қатынасының көмегімен қисықсызықты координаттарый q 1 , q 2 , q 3 енгізілген.
x, y, z - ке қатысты шешетін болсақ, бұлай жазуға болады.
x=φ 1 (q 1 , q 2 , q 3 ) , y=- φ 2 (q 1 , q 2 , q 3 ), z= φ 3 (q 1 , q 2 , q 3 ) (15)
q 1 =C 1 , q 2 =C 2 , q 3 =C 3 - деп ұйғарсақ, С 1 , С 2 , С 3 - тұрақтылар, онда үш үйірлі координаталар бетін аламыз:
f 1 ( x, y, z ) =C 1 , f 2 ( x, y, z ) =C 2 , f 3 ( x, y, z ) =C 3 (16)
Үш жұпты координаталар бетімен шектелген элемент көлеммен жаңа координаталарында қарастарайық. РИСУНОК(44)
АВ қабырғасының бойында q 2 =const, q 3 =const.
АD қабырғасының бойында q 1 =const, q 2 =const.
АC қабырғасының бойында q 1 =const, q 3 =const.
AB, AD және AC қабырғаларына жанама бағытталған косинустары пропорционал сәйкес
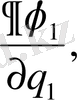
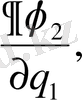
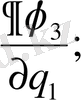
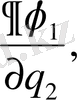
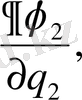
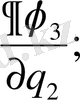
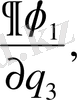
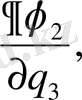
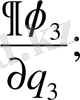
Қабырғалардың ортогональ шарты мынадай түрде болады.
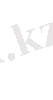
 (
(
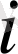 ≠
≠
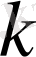 ) (17)
) (17)
Жаңа координаталарда элементтің ұзындығын есептейік.
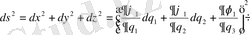 Equation. 3 +
Equation. 3 +
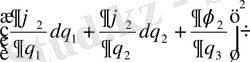 Equation. 3 +
Equation. 3 +
+
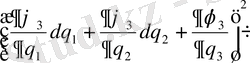 Equation. 3 . (18)
Equation. 3 . (18)
Жақшаларды ашып және ортогональ шартты ескерсек, онда
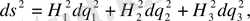 Equation. 3 (19)
Equation. 3 (19)
формуланы аламыз.
Ал
Equation. 3 (20)
элементарлық көлемнің әр қабырғасының бойында бір координата ғана ауысады, сондықтан осы қабырғалардың ұзындығы үшін (19) формулаға сәйкес келіп
,
,
, (21)
аламыз.
Яғни, элемент көлемі мынаған тең:
(22)
Енді кейбір векторлық өрісті A(x, y, z) қарастырайық. Белгілі векторлық анализ формуласымен анықталатын div A есептеп шығарайық.
div A =
(23)
S - М нүктесі бар кейбір
 көлемімен шектелген бет. Осы формуланы 1 -суреттегі dv көлем элементіне қолданамыз. Орташа теоремены пайдаланып А вектор ағынының айырымын қарама - қарсы жақтар, яғни оң және сол жақ арқылы көрсетуге болады.
көлемімен шектелген бет. Осы формуланы 1 -суреттегі dv көлем элементіне қолданамыз. Орташа теоремены пайдаланып А вектор ағынының айырымын қарама - қарсы жақтар, яғни оң және сол жақ арқылы көрсетуге болады.
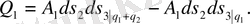
(21) - формуланы назарға алатын болсақ, онда
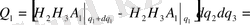 Equation. 3
Equation. 3
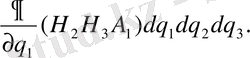 (24)
(24)
Осы сияқты қарама - қарсы жақтар арқылы екі ағынның айырымын есептеп шығаруға болады.
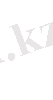 Equation. 3
Equation. 3
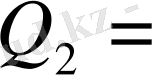 Equation. 3
Equation. 3
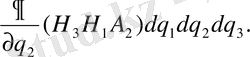 (25)
(25)
және
 Equation. 3
Equation. 3
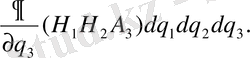 Equation. 3 (26)
Equation. 3 (26)
(22) - ші формуланы пайдаланып және (23) - формулаға
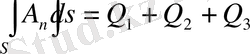 Equation. 3
Equation. 3
мәнін қоятын болсақ, онда қисықсызықты ортогональ координаталарда дивергенция өрнегін аламыз.
div
A
=
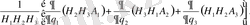 Equation. 3 (27)
Equation. 3 (27)
А өрісі потенциалды деп ұйғарсақ
A=grad u (28)
Онда
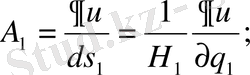 Equation. 3
Equation. 3
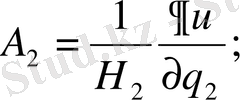 Equation. 3
Equation. 3
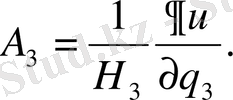 Equation. 3 (29)
Equation. 3 (29)
(27) - формулада А 1 , А 2 , А 3 үшін (29) формуланың өрнегін қоятын болсақ, онда Лаплас операторы үшін өрнек аламыз.
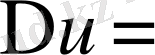 Equation. 3 div grad u=
Equation. 3 div grad u=
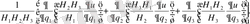 Equation. 3 (30)
Equation. 3 (30)
Лаплас теңдеуі ∆u=0 ортогональ қисықсызықты координаталарда q 1 , q 2 және q 3 келесі турде жаэылады.
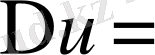 Equation. 3
Equation. 3
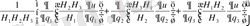 Equation. 3 (31)
Equation. 3 (31)
Екі дербес жағдайды қарастырайық:
- Сфералық координаталар.
Бұл жағдайда
 Equation. 3,
Equation. 3,
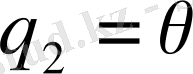 Equation. 3,
Equation. 3,
 Equation. 3
және (15) түрлендіру формуласы мынадай түрге келеді.
Equation. 3
және (15) түрлендіру формуласы мынадай түрге келеді.
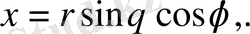 Equation. 3
Equation. 3
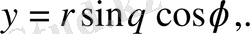 Equation. 3
Equation. 3
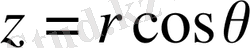 Equation. 3
Equation. 3
ds 2 - ті есептейік:
ds 2 = (sinθ cosϕ dr + r cosθ cosϕdθ - r sinθ sinϕ dϕ ) 2 +
+ (sinθ sinϕ dr + r cosθ sinϕdθ + r sinθ cosϕ dϕ ) 2 +(cosθ dr - r sinθ dθ) 2 ;
Жақшаларды ашып қысқартсақ:
ds 2 = dr 2 + r 2 dθ 2 +r 2 sin 2 θ dϕ 2 ,
Яғни
H 1 =1, H 2 =r, H 3 =r sinθ.
H 1 , H 2 , H 3 мәндерін (31) формулаға қоятын болсақ, онда сфералық координаттар ішінде Лаплас теңдеуін аламыз.
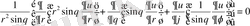
немесе
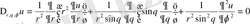 (32)
(32)
2) Цилиндрлік координаттар.
Бұл жағдайда q 1 = ρ, q 2 = φ, q 3 = z;
x= ρ cos φ, y= ρ sin φ, z=z.
Яғни
H 1 =1, H 2 =p, H 3 =1
Цилиндрлік координаттар ішінде Лаплас теңдеуі мына турге келеді.
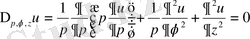 (33)
(33)
Егер ізделінетін u функция z-тен тәуелсіз болса, онда (33) теңдеуі ықшамдалады.
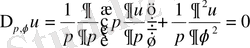 (34)
(34)
- Лаплас теңдеуінің кейбір дербес шешімдері.
Сфералық немесе цилиндрлік симметрияға ие болған, яғни r немесе ρ бір ғана айнымалыға тәуелді Лаплас теңдеуінің кейбір дербес шешімдері қызығушылық тудырады.
Сфералық симметрияға ие болған Лаплас теңдеуінің u=U(r) шешімі кәдімгі дифференциал теңдеуден анықталады.
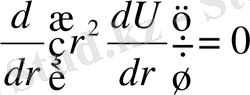
Осы теңдеуді интегралдасақ:
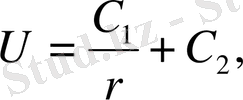
табамыз.
С 1 және С 2 - кез келген тұрақтылар.
С 1 =1, С 2 =0 деп ұйғарсақ, келесі функцияны аламыз.
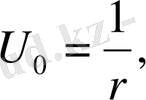 (35)
(35)
Оны кейде кеңістіктегі Лаплас таңдеуінің фундаментал шешімі деп те атайды.
Осы сияқты
u=U(ρ)
деп алып және (33) немесе (34) теңдеуін пайдаланып цилиндрлік немесе айналма симметрияға ие болғанда (екі тәуелсіз айнымалысы бар жағдайда)
U(ρ) = C 1 lnρ+C 2
C 1 =1 және C 2 =0 деп алсақ, онда:
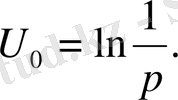 (36)
(36)
U 0 (ρ) - функциясын, екі тәуелсіз айнымалысы үшін кейде жазықтықтағы Лаплас теңдеуінің фундаментал шешімі деп те атайды.
U
0
=
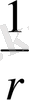 функциясы ∆u=0 теңдеуін барлық жерде қанағаттандырады, бірақ r=0 нүктесінде шексіздікке айналып кетеді. Координат басында орналасқан,
е
зарядының нүктелі өрісі көбейткіш пропорционалына дейінгі дәлдікпен дәл келеді. Осы өрістің потенциалы
функциясы ∆u=0 теңдеуін барлық жерде қанағаттандырады, бірақ r=0 нүктесінде шексіздікке айналып кетеді. Координат басында орналасқан,
е
зарядының нүктелі өрісі көбейткіш пропорционалына дейінгі дәлдікпен дәл келеді. Осы өрістің потенциалы
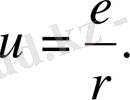
Осы сияқты ln
 Equation. 3 функциясы Лаплас теңдеуін барлық жерде қанағаттандырып, бірақ ρ=0 нүктесінде оң шекпіздікке айналып кетеді және сызықпен зарядталған өріс көбейткішке дейінгі дәлдікпен дәл келеді.
Equation. 3 функциясы Лаплас теңдеуін барлық жерде қанағаттандырып, бірақ ρ=0 нүктесінде оң шекпіздікке айналып кетеді және сызықпен зарядталған өріс көбейткішке дейінгі дәлдікпен дәл келеді.
Оның потенциалы
u=2
e
1
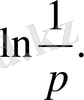
е - бірлік ұзындыққа есептеліген заряд тығыздығы. Осы функциялар гармониялық функциялар теориясында үлкен мәнге ие болғаны.
1. 5 Комплекс айнымалысының гармониялық және
аналитикалық функциясы.
Лаплас теңдеуі үшін екі өлшемді есепті шешудің жалпы әдісі комплекс айнымалысының функция әдісі қолданылады.
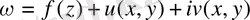
- кейбір z=x+iy комплекс айнымалысының функциясы, сонымен бірге u және v, x және y айнымалылардың нақтылық функциясы болып табылады.
 Аналитикалық функция үшін туындысы бар болатын функция үлкен қызығушылықты тудырады.
Аналитикалық функция үшін туындысы бар болатын функция үлкен қызығушылықты тудырады.
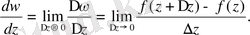
Δz= ∆x +iΔy өсімшесі нөлге көп жолмен ұмтылу мүмкін.
Δz нөлге ұмтылудың әр жолына байланысты шектің өз мағынасы болады. Бірақ ω=(z) функция аналитикалық болса, онда
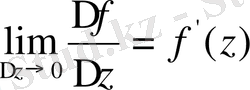
шекгі таңдап алынған жолға тәуелсіз.
Аналитикалық функцияның қажетті және жеткілікті шарттары Коши - Риман шарттары болып табылады.
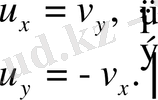 (37)
(37)
Осы шарттарды келесі түрде алуға болады.
ω= u+iv=f(z) аналитикалық функция болсын, туындыларды есептегенде
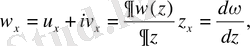
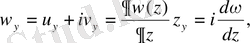
Осы екі арқатынасты анықтайтын
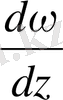 мәнінің теңдігін талап етсек, онда
мәнінің теңдігін талап етсек, онда
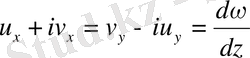
Осыдан Коши-Риман шарттары пайда болады.
Комплекс айнымалы функциясының теориясында, кейбір G облысында z=x+iy жазықтықта бар болып және аналитикалық функцияда барлық ретті туындалар дәреже қатарына жіктеледі. Сондықтан х және у арқылы функциялар u(x, y) және v(x, y) үзіліссіз екінші ретті туындыларға ие болады.
(37) формуланың бірінші теңдігін х арқылы, ал екінші теңдігін у арқылы дифференциалдасақ:
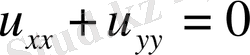 немесе
немесе
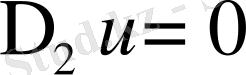
Тап осылай дифференциалдау ретін ауыстыра отырып табамыз
 немесе
немесе
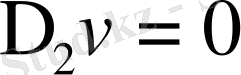
Осылайша аналитикалық функцияның нақты және жорамал бөліктері Лаплас теңдуін қанағаттандырады.
Кейде Коши-Риман шарттарын қанағаттандыратын u және v гармониялық функциямен түйіндес болады.
Туындыны қарастырайық.
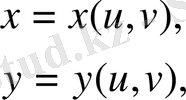
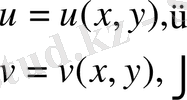 (38)
(38)
Өзара бірмәнді (х, у) жазықтығында кейбір G облысы (u, v) жазықтығында G ’ облысына бейнеленіп, әрбір G облысының нүктесі G ’ облысының нүктесіне сәйкес келеді және керісінше, әрбір G ’ облысының нүктесі G облысының нүктесіне сәйкес келеді.
U=U(x, y)
- G облысының ішінде анықталған кейбір үзіліссіз екі ретті
дифференциалды нақты функция болсын.
Лаплса операторының функциясы
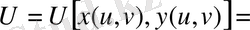
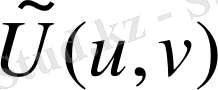
түрлендіруден кейін қалай өзгеретінін анықтайық.
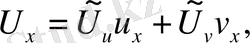
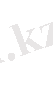
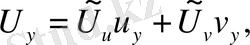
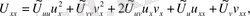
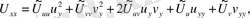
Осыдан
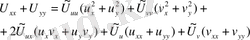 (39)
(39)
Егер u және v гармлниялық функциямен түйіндес болса, онда аналитикалық функцияның көмегімен жүзеге асатын түрлендіру (38) түрлендіруге эквивалентті.
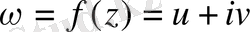
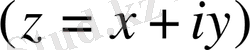 (40)
(40)
Бұл жағдайда Коши - Риман шарты u және v функция үшін мынадай арақатынастар орындалу керек.
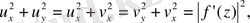
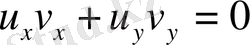
(39) формула мынадай турге келеді.
 (41)
(41)
немесе
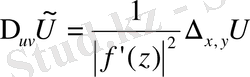 (41
’
)
(41
’
)
Осыдан (40) формуланы түрлендіруден кейін
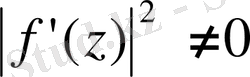 болса, онда G облысындағы U(x, y) гармониялық функция, G
’
облысындағы
болса, онда G облысындағы U(x, y) гармониялық функция, G
’
облысындағы
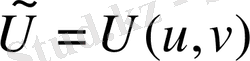 гармонялық функцияға көшеді.
гармонялық функцияға көшеді.
- Кері радиус - векторларды түрлендіру.
Гармониялық функцияларды оқу барсында ылғи кері радиус - векторларды түрлендіруі қолданылады.
 Equation. 3 радиус - сферасында кері радиус - векторларды түрлендіру дегеніміз - координат басынан, сәуледе жатқан М
’
нүктесі әр М нүкте сияқты сәйкес келеді және M
’
нүктенің r
’
радиус - векторлары мен М нүктенің r радиус - векторлары мынадай арақатынаста байланысты.
Equation. 3 радиус - сферасында кері радиус - векторларды түрлендіру дегеніміз - координат басынан, сәуледе жатқан М
’
нүктесі әр М нүкте сияқты сәйкес келеді және M
’
нүктенің r
’
радиус - векторлары мен М нүктенің r радиус - векторлары мынадай арақатынаста байланысты.
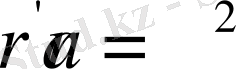 немесе
немесе
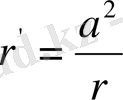 (42)
(42)
Маштаб ұзындығын өзгертуге байланысты a=1 деп есептейік.
Екі тәуелсіз айнымалысы υ(ρ, φ) бар гармониялық функцияны кері радиус - векторлары арқылы түрлендіргенде, ол жай гармониялық функцияға көшетінін көрсетейік:
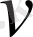 (ρ
’
, φ) =u(ρ, φ) ρ=
(ρ
’
, φ) =u(ρ, φ) ρ=
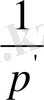 (43)
(43)
υ(ρ, φ) функциясы және сонымен бірге ρ және φ айнымалы функциялары ретінде
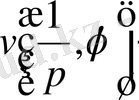 функциясы осы теңдеулерді қанағаттандырады.
функциясы осы теңдеулерді қанағаттандырады.
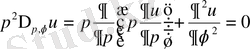
және
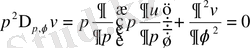
ρ ’ және φ айнымалыларына көшетін болсақ, онда
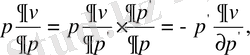
Осыдан
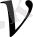 (ρ
’
, φ) ,
(ρ
’
, φ) ,
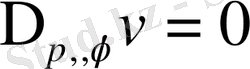 теңдеуін қанағаттандытады, өйткені
теңдеуін қанағаттандытады, өйткені
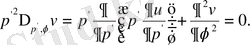
Үш тәуелсіз айнымалыларға көшетін болсақ, онда
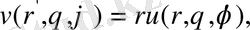
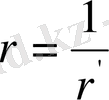 (44)
(44)
функция Лаплас теңдеуін
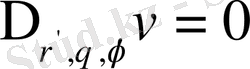 қанағаттандырады.
қанағаттандырады.
(44) түрлендіруін кейде Кельвин түрлндіруі деп атайды.
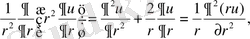 (45)
(45)
яғни
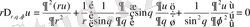
немесе

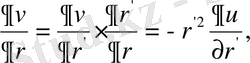
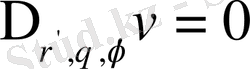 теңдеуін
теңдеуін
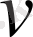 қанағаттандыратын көреміз, яғни
қанағаттандыратын көреміз, яғни
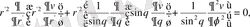
немесе
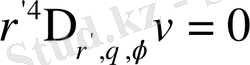
2. Гармониялық функцияның жалпы қасиеттері.
Шеттік есептерді шешу барысында және жалғыздық теоремасын дәлелдеу кезінде көп қоданылатын интегралды формуланың маңызды нәтижелерінің бірі - максималды мәннің қағидасы болып табылады. Мында Лаплас теңдеуі үшін ішкі және сыртқы шеттік есептердің математикалық құрлымы беріледі және бұл есептердің шешілуінің тұрақтылығы және жалғыздығы дәлелденеді.
2. 1 Грин формулалары. Шешімнің интегралды көрінісі.
Остроградский формуланың тура нәтижесі Грин формулаларымен эллипстік типтегі теңдеулерді шешу барысында жиі қолданылады.
Остроградский формуласы қарапайым жағдайда мынадай түрде болады2.
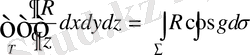 (1)
(1)
мұнда
 -
-
 тегіс бетпен шектелген кейбір көлем,
тегіс бетпен шектелген кейбір көлем,
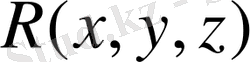 -
-
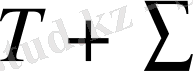 ішінде үзіліссіз және
ішінде үзіліссіз және
 ішінде үзіліссіз туындысы бар кез-келген функция,
ішінде үзіліссіз туындысы бар кез-келген функция,
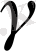 -
-
 - ға ішкі нормаль және z осіне бағыт арасындағы бұрыш. z бойынша интегралдау орындасақ бұл формуланың әділдігіне көз жеткіземіз.
- ға ішкі нормаль және z осіне бағыт арасындағы бұрыш. z бойынша интегралдау орындасақ бұл формуланың әділдігіне көз жеткіземіз.
Остроградский формуласы көбінесе мына түрде жазылады 1 .
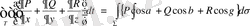 (2)
(2)
мұнда
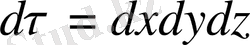 - көлем элементі,
- көлем элементі,
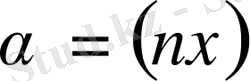 ,
,
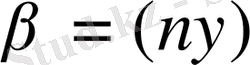 ,
,
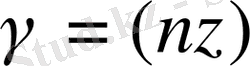 - координаталық осьтері бар
- координаталық осьтері бар
 бетіне n ішкі нормаль бұрыштары, R, P, Q-кез келген дифференциалды функциялар3
бетіне n ішкі нормаль бұрыштары, R, P, Q-кез келген дифференциалды функциялар3
Егер
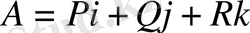 кейбір вектордың компоненттері ретінде P, Q. R - ді қарастыратын болсақ, онда Остроградскийй формуласын келесі түрде жазуға болады.
кейбір вектордың компоненттері ретінде P, Q. R - ді қарастыратын болсақ, онда Остроградскийй формуласын келесі түрде жазуға болады.
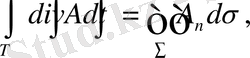 (2
‘
)
(2
‘
)
мұнда
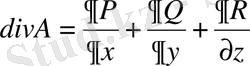
және ішкі нормаль бойында А векторын құрастыратын
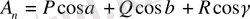 .
.
Енді Грин формуласының нәтижесіне келейік
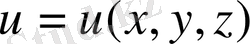 және
және
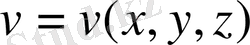
 ішінде үзіліссіз екінші туындысы бар және
ішінде үзіліссіз екінші туындысы бар және
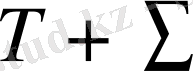 ішінде өздерінің бірінші туындыларымен узіліссіз болсын.
ішінде өздерінің бірінші туындыларымен узіліссіз болсын.
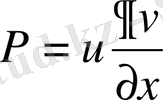
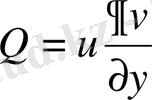
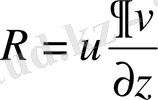
деп ұйғарып және (2 ‘ ) Острогралский формуласын қолдана отырып, бірінші Грин формуласына келеміз.
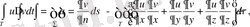 (3)
(3)
мұнда
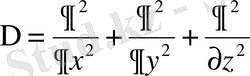 - Лаплас операторы,
- Лаплас операторы,
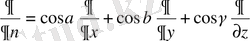 - ішкі нормаль бағыты бойынша туынды.
- ішкі нормаль бағыты бойынша туынды.
Егер
gradu gradv=
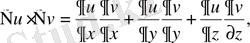
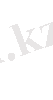
арақатынасты ескерсек, онда Грин формуласын мына түрде көрсетуге болады.
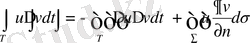 (3
‘
)
(3
‘
)
u және v функцияларын ауыстыра отырсақ:
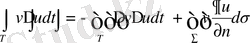 (4)
(4)
(3 ‘ ) -теңдігінен (4) -тендігін азайтсақ, екінші Грин формуласын аламыз.
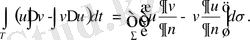 (5)
(5)
 облысы бірнеше беттермен шектеле алады .
облысы бірнеше беттермен шектеле алады .
 облысын шектейтін барлық беттер бойынша беттік интегралдарды алғанның өзінде де Грин формулалары қолданылады.
облысын шектейтін барлық беттер бойынша беттік интегралдарды алғанның өзінде де Грин формулалары қолданылады.
Екі айнымалысы бар
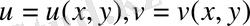 функция үшін ұқсас Грин формулалары орын алады. С шекарасы бар S облысында екінші Грин формуласы мынадай
функция үшін ұқсас Грин формулалары орын алады. С шекарасы бар S облысында екінші Грин формуласы мынадай
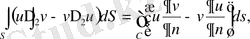
түрде болады. Мұнда dS=dxdy, ds-бойындағы доға элементі,
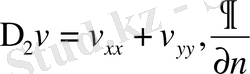 - n нормалі С контурына іштей бағытталған туынды.
- n нормалі С контурына іштей бағытталған туынды.
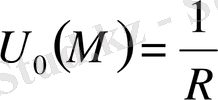 - функциясы, мұндағы
- функциясы, мұндағы
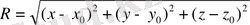 - M(x
0
, y
0
, z
0
) және М(х, у, z) нүктелері арасындағы арақашықтық және егер
- M(x
0
, y
0
, z
0
) және М(х, у, z) нүктелері арасындағы арақашықтық және егер
 болса, онда ол Лаплас теңдеуін қанағаттандырады.
болса, онда ол Лаплас теңдеуін қанағаттандырады.
 облысында екінші туындысыбар және
облысында екінші туындысыбар және
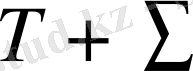 облысында бірінші туындысымен бірге үзіліссіз u(M) - гармониялық функция болсын.
облысында бірінші туындысымен бірге үзіліссіз u(M) - гармониялық функция болсын.
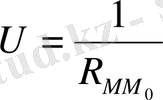 функциясын қарастырайық.
функциясын қарастырайық.
мұндығы М
0
-
 облысының кейбір ішкі нүктесі.
облысының кейбір ішкі нүктесі.
 ішінде бұл функция
M(x
0
, y
0
, z
0
)
нүктесінде үздіксіздіктің үзілісі бар болса, онда
ішінде бұл функция
M(x
0
, y
0
, z
0
)
нүктесінде үздіксіздіктің үзілісі бар болса, онда
 облысында
облысында
 және
және
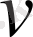 функцияларына Грин формуласын қолдануға болмайды. Бірақ
функцияларына Грин формуласын қолдануға болмайды. Бірақ
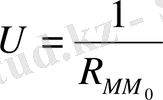 функциясы
функциясы
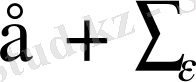 шекарасымен
шекарасымен
 - К
ε
облысында шектелген. Мұндағы К
ε
-
- К
ε
облысында шектелген. Мұндағы К
ε
-
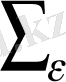 бетімен және М
0
нүктесіндегі центрімен ε шар радиусы. (РИС 45)
бетімен және М
0
нүктесіндегі центрімен ε шар радиусы. (РИС 45)
 - К
ε
облысында
- К
ε
облысында
 және
және
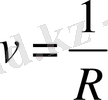 функцияларына екінші Грин формуласын қолдана отырып
функцияларына екінші Грин формуласын қолдана отырып
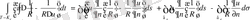 (6)
(6)
формуласын аламыз.
 еңдіктің оң бөлігіндегі ақырғы екі интегралы ғана ε - ге тәуелді.
еңдіктің оң бөлігіндегі ақырғы екі интегралы ғана ε - ге тәуелді.
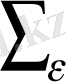 - бетіндегі
- бетіндегі
 - К
ε
облысына сыртқы нормаль бойынша туындыны азайта отырып
- К
ε
облысына сыртқы нормаль бойынша туындыны азайта отырып
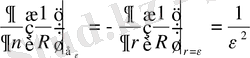 ,
,
табамыз.
Осыдан
 (7)
(7)
 * -
* -
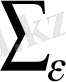 бетіндегі u(M) функцияның орташа мәні. Үшінші интегралды түрлендірсек
бетіндегі u(M) функцияның орташа мәні. Үшінші интегралды түрлендірсек
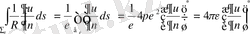 (8)
(8)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz