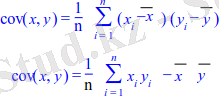Жапонияның 1987-2016 жылдарындағы ЖІӨ мен шығынның жұптық сызықтық регрессиялық талдауы

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Жоспар:

І. КІРІСПЕ

Талдау жүргізілетін коэффициенттерге анықтама (теория)

ІІ. НЕГІЗГІ БӨЛІМ

а) Жапония мемлекетінің ЖІӨ мен шығын көрсеткіштерін excel-ге орналыстыру

ә) Алынған көрсеткіштерге талдау жүргізе отырып, регрессия моделін құрастыру:

Регрессия моделінің корреляция тығыздығын анықтау
Жұптық сызықтық регрессия моделін құру
Коэффиценттің сапасын анықтау. Аппроксимация
Детерминация коэффицентін анықтау
Регрессияның статистикалық мәнділігін зерттеу
Параметрлердің статистикалық мәнділігін зерттеу
Сенімділік интервалын есептеу
Икемділік коэффицентін анықтау

б) Көрсеткіштерге сүйене отырып, график құру

ІІІ. ҚОРЫТЫНДЫ

Жүргізілген талдаудың қорытындысын шығару.

І. Теория

Регрессия моделінің корреляциялық тығыздығы.

Корреляция коэффициенті - 2 айнымалылар арасындағы байланыс тығыздығын көрсетеді.

Корреляция коэффициентінің анықтамасынан оның келесі қасиеттері шығады.

1°. Корреляция коэффициенттерінің қабылдайтын мәндері [-1, +1], яғни -1 < r < 1

2°. Егер r = 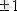онда тандаманың нүктелері бір түзу үстінде жатады (регрессия түзулері беттессе, онда ) .

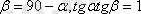3°. Егер корреляция коэффициентінің мәні ±1-ге жақын болса,
онда X пен У арасында күшті сызықтық тәуелділік бар деп
есептеледі.

4°. Егер r мәні нөлге жақын болса, онда айнымалылар арасында корреляциялық тәуелділік нашар деп есептеледі ( r < 0, 4 болғанда X пен У арасында ешқандай сызықтық корреляция болмайды) .

5°. Корреляция коэффициенті өлшемсіз (безразмерная) шама, оның мәні X және У шамаларының өлшеміне және координаталардың бас нүктесінің орналасуына байланыссыз болады.

Корреляция коэффициентi . Тәуелдiлiктiң дәл өлшемi онымен тығыз байланысқан

корреляция коэффициентi болып табылады. Ковариацияның екi формасы бар - теоретикалық және таңдамалық.

Таңдамалық ковариация - екi айнымалы арасындағы өзара байланыс өлшемi болып табылады. x және y айнымалылары арасындағы таңдамалы ковариация келесi формулалармен анықталады:

Ковариацияны есептеудiң негiзгi ережелерi:

1) Егер y = u +v болса, онда cov(x, y) = cov(x, u) + cov(x, v. ) .

2) Егер y = az болса, мұндағы a-тұрақты, онда cov(x, y) = acov(x, z)

3) Егер y = a-тұрақты болса, онда cov(x, y) =0.

n байқау үшiн x және y кездейсоқ шамалардың теоретикалық ковариациясын олардың орташа шамалардан ауытқуларының көбейтiндiсiнiң математикалық күтiмi ретiнде анықтаймыз: pop, cov(x, y) = ζ2x=E{(x- μx) (y- μy) }

n байқаудан тұратын таңдама үшiн таңдамалы дисперсия таңдамадағы орташа квадраттық ауытқу ретiнде анықталады:

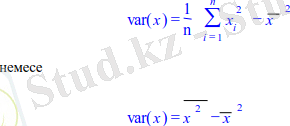
2. Жұптық сызықтық регрессия моделі - екі айнымалы арасындағы статистикалық байланыс .

Функционалды тәуелділік түрін таңдау модель спецификациясы, ал түсіндіруші айнымалылар құрамын анықтау айнымаллар спецификациясы деп аталады. Олар эконометрикалық модельдеудің құраушылары болып табылады.

Егер модель бір ғана түсіндіруші айнымалыны қамтыса, яғни к=1, онда ол жұптық регрессия, ал к›1 болса, көптік регрессия деп аталады. Жалпы бастапқыда тәуелдiлiктi тапқан соң, параметрлердi бағалауға көшемiз. β0, β1, β2, …, βn параметрлерi статистикалық мәлiметтер негiзiнде анықталады.

$y = a + b*x$

$b = \frac{cov(xy) }{var(x) }$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a = \overline{y} - b*\overline{x}$

Аппроксимация- жуықтау (лат. approximare - жақындау, жуықтау) .

Аппроксимация - модельдің қаншалықты сапалы екендігін көрсетеді. Оның мәні 10%-дан аспайды. Асып еткен жағдайда, модельдің сапасыздығын көрсетеді.

$A = \frac{1}{n}*\sum_{i = 1}^{n}{\left \frac{y - \widehat{y}}{y} \right*100\%}$

Детерминация коэффициенті.

Егер p факторы бар модель құрылса, онда ол үшін детерминация көрсеткіші $R^{2}$ детерминация көрсеткіші есептелуі тиіс, яғни шешуші белгінің вариациясын анықтау керек. Модельге кірмейтін факторларды 1- $R^{2}$ түріндегі қалдық дисперсияға $S^{2}$ байланысты шешу керек. Егер регрессияға қосымша p+1 факторлары енсе, онда детерминация коэффициенті өседі, ал қалдық дисперсия кемиді. Яғни, бұл шарт орындалмаса, онда енгізілген факторлар модельдің дұрыс құрылғанын көрсетпейді, сондықтан бұл факторлар артық деп саналады.

$R^{2} = r_{xy}^{2}$

Яғни, шыққан мән у вариацияның х вариацияға қаншалықты тәуелді екенін көрсетеді.

Регрессиялық статистика мәнділігі.

Теңдеудің жалпы статистикалық мәнділігі Фишердің Fкритикасы бойынша есептеледі.

Егер, Fфактор˃Fкритика болса, онда - нөлдік гипотеза қабылданбайды, детерминация коэффициенті статистикалық мәнді, модель кездейсоқ емес және сапалы болып табылады.
Егер, Fфактор˂Fкритика болса, онда - нөлдік гипотеза қабылданады, детерминация коэффициенті статистикалық мәнсіз, модель кездейсоқ және сапалсыз болып саналады.

$F_{стат} = \frac{R^{2}*(n - 2) }{(1 - R^{2}) }$

H ₀ : R ² =0

k ₁ =1; k ₂ =n-2

Параметрлердің статистикалық мәнділігі.

Т. Стьюдент - а және b корреляция коэффициенттерінің мәнділігін анықтау үшін қажет. Оны анықтау үшін оның сенімділік ықтималдылығын есептеу керек:H ₀ : r _xy =0; а=0; b=0

${S^{2}}_{қ} = \frac{\sum_{i}^{}{(y - \widehat{y) }}^{2}}{n - 2}$

$с. қ. (а) = \sqrt{\frac{S_{қ}^{2}}{n}*(1 + \frac{{\overline{x}}^{2}}{var(x) }}$

$с. қ. (b) = \sqrt{\frac{S_{қ}^{2}}{n*var(x) }}$

$с. қ. \left( r_{xy} \right) = \sqrt{\frac{1 - r_{xy}^{2}}{n - 2}}$

$t_{a} = \frac{a}{с. қ. (a) }$

$t_{b} = \frac{b}{с. қ. (b) }$

$t_{r_{xy}} = \frac{r_{xy}}{с. қ. (r_{xy}) }$

tkr - 0, 05-0, 01 (екі жақты) мәнділік деңгейдегі Стьюденттің t критикалық мәні

ta ˃ tkr - Н0 қабылданбайды, коэффициент статисткалық мәнді, сапалы және кездейсоқ емес ;

tb ˂ tkr - Н0 қабылданады, коэффициент статисткалық мәнсіз, сапасыз және кездейсоқ;

trxy ˂ tkr - Н0 қабылданады, коэффициент статисткалық мәнсіз, сапасыз және кездейсоқ.

Сенімділік қатысты сипатталады. Егер 5% мәнділік деңгейі қабылданса, соған сәйкес сенімділік интервалы 95% деп саналады.

а шамасы үшін сенімділік интервалы:

$\mathrm{\Delta}a = t_{крит}*с. қ. (a)$

b шамасы үшін сенімділік интервалы

$\mathrm{\Delta}b = t_{крит}*с. қ. (b)$

$\lbrack a \pm \mathrm{\Delta}a\rbrack$ $\lbrack b \pm \mathrm{\Delta}b\rbrack$

Икемділік коэффициенті:

$Э_{xy} = b*\frac{\overline{x}}{\overline{y}}$

Яғни, х 1 % жоғарыласа, у қанша өлшемге өзгергенін көрсетеді.

ІІ. Есептеу жүргізу

Мен у және х көрсеткіштері ретінде - Жапония мемлекетінің ЖІӨ және сол бойынша шығынын алдым. Көрсеткіштер 1987-2016 жылдар арлығын қамтиды. Демек, байқау саны, n=30.

Корреляция коэффициентін табу үшін:

$r_{xy} = \frac{cov(xy) }{\sqrt{var(x) *var(y) }}$

cov(xy) =

0, 403

cov(xy) =: var(x) =

0, 403: 1, 107

cov(xy) =: var(y) =

0, 403: 0, 277

Менің есептеуім бойынша, корреляция коэффициенті 0, 728-ге тең. Корреляция коэффициенті [-1; 1] аралығында жатады. Мендегі көрсеткіш 1-ге жақын болғандықтан, айнымалылар арасында қатаң, тығыз байланыс бар.

Модель:y=a+bx

$b = \frac{cov(xy) }{var(x) }$ = 0. 365

$a = \overline{y} - b*\overline{x}$ = 3. 667

$\widehat{y}$ табу үшін: $\widehat{y}$ = a+bxi

Бұл есептеуде у пен $\widehat{y}$ тең болуы қажет. Яғни, менде у = $\widehat{y}$ = 159. 434

Аппроксимация:A=1n*∑i=1ny−ŷy*100%A = \frac{1}{n}*\sum_{i = 1}^{n}{\left \frac{y - \widehat{y}}{y} \right*100\%}

Ол - модельдің қаншалықты сапалы екендігін көрсетеді. Оның мәні 10%-дан аспайды. Менде 430, 94 - 10-нан асып кетті. Демек, аппроксимация бойынша модель - сапасыз.