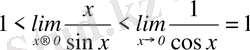Ақырсыз кішкене және ақырсыз үлкен функциялар

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .3

1 Функцияның нүктедегі шегі
1.1 Функцияның нүктедегі шегі түсінігі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .5
1.2 Анықтамалар мен түсініктер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... ... ... 8

2 Функцияның нүктедегі шегін есептеудің әдістері
2.1 Шегі бар функциялардың қасиеттері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... .13
2.2 Ақырсыз кіші және ақырсыз үлкен функциялар ... ... ... ... ... ... . ... ... ... ... ... .16

Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .20

Пайдаланылған әдебиеттер тізімі ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ... ... 22

Кіріспе

Математика - нақты өмірдегі сандық қатынастар мен кеңістіктік формалар туралы ғылым. Математикада математикалық модельдер зерттеледі. Ол нақты құбылыстардың тура математикалық модельдері болуымен қатар осы модельдерді зерттеуге арналған (структуралар) объект болуы мүмкін. Бір математикалық модель тура мазмұны жағынан бір-бірінен қашық жатқан нақты құбылыстардың қасиеттерін көрсетуі мүмкін. Мысалы, бір дифференциалдық теңдеу халықтың өсу процессін де жəне макроэкономикалық динамикасын да көрсетеді. Математика үшін қарастырылып отырған объектілердің табиғи мəні емес, олардың арасындағы қатынастардың маңызы зор. Математика жаратылыс ғылымдарында, инженер-техникалық жəнегуманитарлық зерттеулерде маңызды роль атқарады. Ол көптеген білім бөлімдерінде тек қана сандық есептеу жасау үшін ғана емес, сонымен қатар дəлірек зерттеудің тəсілі жəне ұғымдар мен проблемалардың шекті тура тұжырымдарын беру құралы болады. Адам өміріндегі əртүрлі салалардағы прогресс жетілдірілген логикалық жəне есептеу аппараты бар қазіргі замандағы математикасыз мүмкін емес.
Шек - математиканың негізгі ұғымдарының бірі. Шектердің қазіргі теориясы ХIХ ғасырдың басында қалыптаса бастады. Шек ұғымы алғаш рет О.Коши еңбектерінде қолданылды. Тізбек пен функция шектерінің теориясы Б.Больцано мен К.Вейерштрасстың еңбектері негізінде қалыптасты.
Ежелгі дәуір математиктері (Евклид, Архимед) аудандар мен көлемдерді табу үшін шын мәніндегі шексіз қатарларды пайдаланған. "Жинақтылық" терминін шотланд математигі және астрономы Дж. Грегори (1638 -- 1675) қатарлар үшін қолданды (1668). 18 ғ-да жинақтылық ұғымы шашыраңқы қатарларды талдауда кеңінен қолданыла бастады (Л.Эйлер). Қатарлардың жинақтылықтығын зерттеудің дәлірек әдістері 19 ғ-да жасалды (О.Коши, Н.Абель, Б.Больцано, К.Вейерштрасс, т.б.). Бірқалыпты Жинақтылық ұғымы Н.Абельдің (1826), Ф.Зейдельдің (1847 -- 48) және Дж. Стокстің (1848) еңбектерінде тұжырымдалды. Функциялар теориясының, функционалдық анализдің және топологияның дамуына байланысты жинақтылық ұғымы одан әрі кеңейтілді.
Математика қолданбалы есептерді шешуге арналған күшті құрал жəне ғылымның əмбебап тілі ғана емес, сонымен қатар ол негізгі мəдениеттің элементі де болып есептеледі. Сондықтанда математикалық білім осы заманға экономистерді фундаментальды дайындау жүйесіндегі маңызды бөлім болады.
Математиканың айтылмыш тараулары, әсіресе математикалық анализ 18ғасырда одан әрі дамыды.
Бұл салада ұлы математиктер Л.Эйлер мен Ж.Лагранж ерекше еңбек сіңірді. Осы ғалымдар мен француз математигі А.Лежандр еңбектерінде сандар теориясы алғаш рет жүйелі ғылым санатына қосылды.
Алгебрада швейцар математигі Г.Крамер (1750) сызықтық теңдеулер жүйесін шешу үшін анықтауыштарды енгізді. Ағылшын математигі А Муавр мен Л.Эйлердің көрсеткіштік және тригонометриялық функциялардың байланысын көрсететін формулалары комплекс сандарды математикадағы қолдану өрісін кеңейте түсті. И. Ньютон, шотланд математигі Дж. Стирлинг, Л. Эйлер және П.Лаплас шектеулі айырымдарды есептеудің негізін қалады. К.Гаусс 1799 жылы алгебраның негізгі теоремасының бірінші дәлелін жариялады.
Математикалық анализ әсіресе дифференциалдық теңдеулер әдістері механика мен физиканың, сондай-ақ техникалық процестердің заңдарын, математикалық өрнектеудің негізін қалады; жаратылыс тану мен техниканың ілгерілеуі осы әдістерге тікелей байланысты болды.
Ағылшын математигі Б. Тейлор (1715) кез келген функцияларды дәрежелік қатарға жіктеу жөніндегі өзінің формуласын ашты. 18 ғасыр математиктері үшін қатарлар анализдің ең бір қуатты, икемді құралына айналды. Л. Эйлер, Ж. Лагранж бірінші ретті, ал Л. Эйлер, Г. Монж, П. Лаплас екінші ретті дербес туындылы дифференциалдық теңдеулердің жалпы теориясының негізін қалады.
Жұмыстың мақсаты: функцияның нүктедегі шегі және тамаша шектерді теориялық тұрғыда негіздеп, функцияның нүктедегі шегін табуды үйрену, есептер щығару әдістемесін жетілдіру.
Жұмыстың мідеттері: функцияның нүктедегі шегі және тамаша шектер тақырыптарының оқулықтарда баяндалуына талдауды жүзеге асыру.

1 Функцияның нүктедегі шегі

1.1 Функцияның нүктедегі шегі түсінігі

Функцияның нүктедегі шегіне анықтама берер алдында бірнеше мысалдар қарастырайық, 1-мысал:
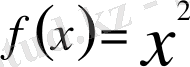функцифсы берілсін. Бұл сан бүкіл сан осіне анықталған. Мәселен, х=3 нүктесінде анықталған. Егер х айнымалысының мәндері 3-ке жақындай түссе, онда 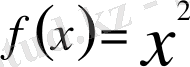функциясының сәйкес мәндері 9-ға жақындайды. Мысалы оны мына кестеден байқауға болады:

х
2,9
2,95
2,98
3
3,02
3,05
3,1
x2
8,41
8,7025
8,8804
9
9,1204
9,3025
9,61

Жалпы, ε0 қаншалықты аз сан болса да, x2 -9 тенсіздік орындалатындай х-тін мәндерін табуға болады.Ол үшін х айнымалысының мәндері 3-ке мейлінше жақын болуы жеткілікті.Сондықтаң х айнымалысының мәндері 3-ке ұмтылатындай болып өзгерсе, 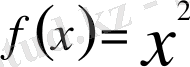функциясының сәйкес мәндері 9-ға жақындайды.Бұлжағдайда 9санын 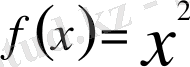функциясының х аргументі 3-ке ұмтылғандағы шегі деп айтады. Оны былай жазады:

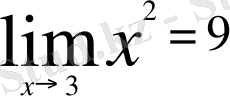
2-мысал:

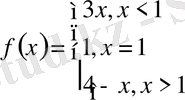
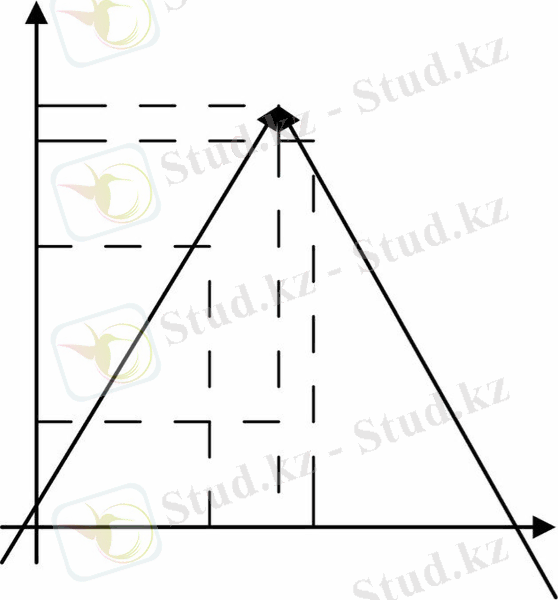
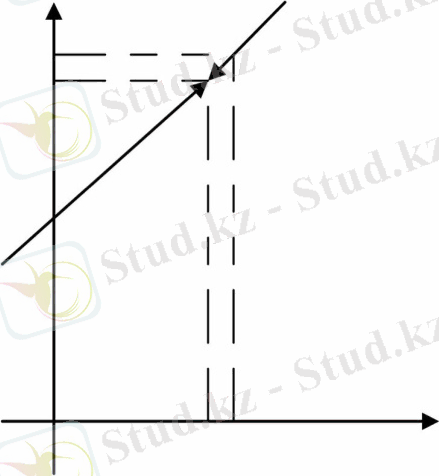
функциясының х=1нүктесіндегі шегі қарастырайық.Бұл функцияның графигі суретте бейнеленген . Осы графиг х аргументі 1-ге ұмтылғанда (оң жағынан болса да) функцияның сәйкес мәндері 3-ке жақындайтынын көреміз .
Яғни,
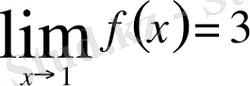
Ал,
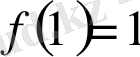
Сонымен,

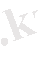
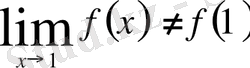
Анықтама. нүктесінің маңайы осы нүкте жататын кез келген интервал.
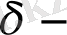Дербес жағдайда, нүктесінің маңайы 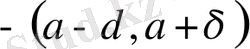интервалы. 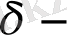маңайы 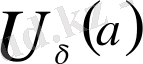түрінде белгіленеді.
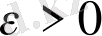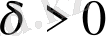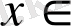
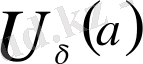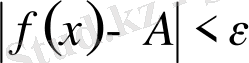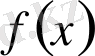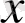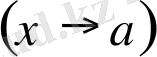Анықтама. Егер кез келген саны үшін саны табылып, кезкелген үшін теңсіздігі орындалса, онда А саны функциясының шамасы ға ұмтылғандағы шегі деп аталады да, 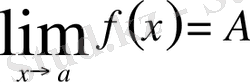түрінде белгіленеді.
Ескерту: 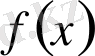функциясы нүктесінде анықталуы да, анықталмауы да мүмкін.
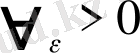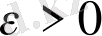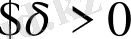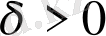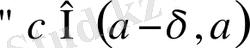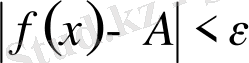Анықтама. Егер (кезкелген ) саны, үшін ( саны) табылып, үшін теңсіздігі орындалса, онда А саны 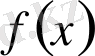функциясының тің ға сол жақтан ұмтылғандағы шегі немесе 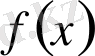функциясының нүктесіндегі сол жақ шегі делінеді. Белгіленуінде: .
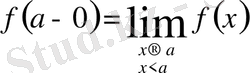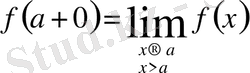
Анықтама. Жоғарыдағыдай 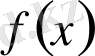функциясының нүктесіндегі оң жақ шегі деп аталады.

Бірінші және екінші тамаша шектер.
Бірінші тамаша шек. Құрамында тригонометриялық функциялар бар өрнектердің шектерін есептегенде бірінші тамаша шекті қолданады: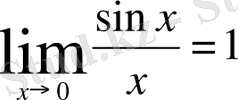 . Дәлелдеу: Радиусы бірге тең шеңбер аламыз. , сонда:

, мұндағы

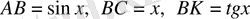
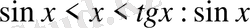
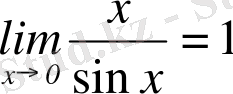
1-мысал.
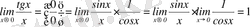
2-мысал. .
Екінші тамаша шек: .
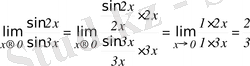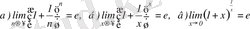Мұндағы е 2,718282... - иррационал сан.
3-мысал. Шекті есептеу керек

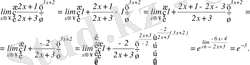
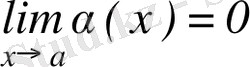Шексіз аздарды салыстыру. Екі шексіз аз шамаларды салыстыру үшін олардың қатынасын қарастырады. - ш.а.ш. болсын, яғни және .
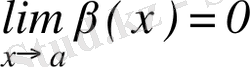1. Егер 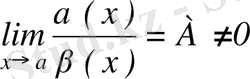болса, онда 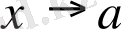ұмтылғанда ш.а.ш.-ның аздық реттері бірдей дейді.
2. Егер 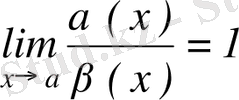болса, онда 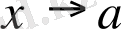ұмтылғанда шексіз аз шамалар эквивалентті деп аталады және 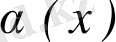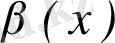деп белгіленеді.
Мысал. 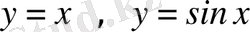шексіз аздар 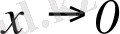ұмтылғанда эквивалентті, бұл бірінші тамаша шектің қасиетінен шығады.
Теорема. 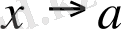ұмтылғанда 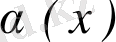ш.а. болсын, онда:
1. ; 2. ;
3. ; 4. ;
5. ; 6. , ;
Теорема. Егер ш.а.ф. - ды оларға эквивалентті функциялармен алмастырса, онда екі ш.а.ф. қатынасының шегі өзгермейді.
4-мысал. ,

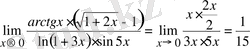себебi, .

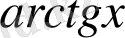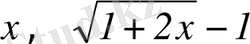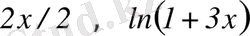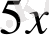1. 2 Анықтамалар мен түсініктер

y f (х) функциясы а нүктесінің белгілі бір U (а) маңайында анықталған болсын ( функцияның а нүктесінің өзінде анықталуы маңызды емес).
1-анықтама. Егер кез келген 0 саны бойынша f функциясының анықталу аймағында жататын және

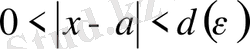
теңсіздіктерін қанағаттандыратын барлық x сандары үшін

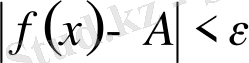
теңсіздігі орындалатындай () 0 саны табылса онда А саны f (x) функциясының а нүктедегі шегі деп аталады да,

⇒

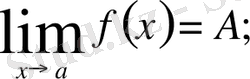
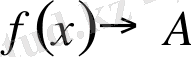
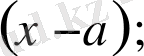
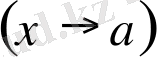
символдарының бірімен белгіленеді.

1-мысал. Дәлелдеу керек: limх--а x2=1.
x2 функциясын 1 нүктесінің белгілі бір мысалы О1 (1) = (0; 2) маңайында қарастырайық. х (0; 2) үшін

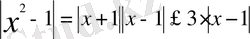
теңсіздігі орындалады. Егер кез келген 0 саны берілсе онда

= min 1; ε3 деп алуға болады (мұндағы 1 саны 1-нүктесінің маңайының радиусі).
Сонда 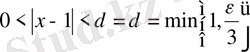қанағаттандыратын кез келген х үшін

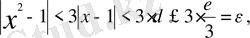
яғни x2-1 ε теңсіздігі орындалады. Бұл - 1-анықтама бойынша

limх--а x2 =1 деген сөз.
2-мысал. Теңдікті дәлелдеу керек:
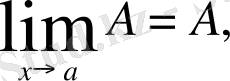
Шынында да, қандай да бір 0 оң саны берілсе,

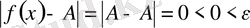теңсіздігі кез келген x нүктесінде

орындалатыны анық.

2-анықтама. Егер n N, хn a шартын қанағаттандыратын а санына жинақталатын әрбір xn D (f) тізбегіне сәйкес келетін f (хn) тізбегінің шегі бар және ол А санына тең болса:
limn--infinity f(хn) =А, онда А саны f (х) функциясының а нүктесіндегі шегі деп аталады да, limх--а f(х)=А немесе f(х)--А (х--а) символдарының бірімен белгіленеді. Егер мұнда А шегі , + , ақырсыздықарының біріне тең болса, онда f (х) функциясы x a ұмтылғанда ақырсыз үлкен шама деп аталады. (1) және (2) анықтамалар - пара-пар. Біз мұнда оның дәлелдеуіне тоқталмаймыз. 1, 2 анықтамаларды сәйкес Коши, Гейне анықтамасы дейді.
Ескерту. Егер функцияның берілген нүктеде шегі бар болса, онда ол нақты (ақырлы) сан немесе + , ақырсыздықтарының бірі болуы мүмкін: limх--а f(х)=А, -infinity=А=+infinity .

3-мысал. Шекті табу керек: limх--2x2- 4x - 2.
х --2 ұмтылғанда функцияның x 2 нүктесіндегі мәні назарға
алынбайтындықтан кез келген x 2 үшін x2- 4x - 2 =х+2. Ал x 2 өрнегіндегі х орнына, 2-анықтамаға сәйкес, xn 2 -ге ұмтылатын кез келген nx тізбекті қойып сандық тізбектер шегінің қасиеттерін пайдаланамыз
limх--2x2- 4x - 2 =limх--2 х+2= limn--infinityxn+2=2+2 =4.
Функцияның шегін есептегенде xn тізбегін көрсетіп жазып жатпайды, x-ті 2-ге ұмтылатын кез келген тізбек деп қабылдап қысқартып жазады:
lim х--2x2- 4x - 2 =limх--2 х+2= limn--infinityх+2=4.

4-мысал. f(x) sin 1х функциясының x 0 нүктесіндегі шегі жоқ екенін дәлелдеу керек.

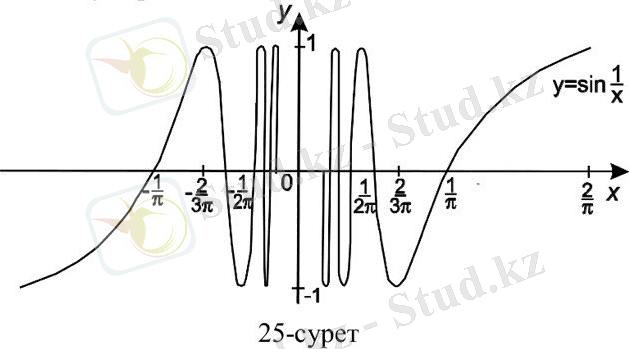
f(x) sin 1х функциясы - х =0 кез келген маңайының барлық х !=0 нүктелерінде анықталған және тақ функция. 0-ге ұмтылатын xk= 2PI (2k+1) тізбекке сәйкес келетін
fxk= sin PI (2k+1)2=cos PIk=(-1)k
тізбегінің шегі жоқ. (4.3.2.п. 3-мысалды қараңыз). Олай болса 2-анықтама бойынша f(x) sin 1х функциясының x 0 нүктесінде шегі жоқ (25-сурет). Анықтама. Егер кез келген 0 саны бойынша
a x a a x a (1)
теңсіздіктерін қанағаттандыратын барлық х-тер үшін
fx-Аε
теңсіздігі орындалатындай () 0 саны табылса онда А саны f (х) функциясының а нүктедегі оң жақ (сол жақ) шегі деп аталады да,

lim х--а+ f(х)=А; limх -- ах а f(х)=А, f(а+)=А,

(lim х--а-fх=А, limх -- ах а f(х)=А, f(а-)=А )
символдарының бірімен белгіленеді.

Теорема. lim х--а f(х) шегі бар болуы lim х--а+ f(х), lim х--а-fх үшін шектері бар әрі олардың өзара тең болуы қажетті және жеткілікті яғни
lim х--а+ f(х) = lim х--а-fх=А ⇔ (2)

⇔ lim х--аfх=А. (3)

Теореманы А-нақты сан үшін дәлелдейміз ( A немесе A үшін дәлелдеуді оқушыға қалдырамыз). Шынында да (2), теңдіктерді келесі түрде жазуға болады:

∀ε0 ∃δε0: ∀x:0x-aδ, xa ⇒ fх-Aε;

∀ε0 ∃δε0: ∀x:0x-aδ, xa ⇒ fх-Aε;

(2) қатыстардағы екі теңдіктің де бір мезгілде орындалуына x a мен x a шарттарының екеуі де керек. х a , x a x a екенін ескеріп, алдыңғы кванторлар тілінде жазылған анықтаманы біріктіріп

∀ε0 ∃δε0: ∀x:0x-aδ, (ε) ⇒ fх-Aε

түрінде жазуға болады. Ал бұл (3) теңдіктің анықтамасы. Мысалы

lim х--2+x-2x-2 = limх--2x2x-2x-2 = 1, limх--2-x-2x-2 = limх--0x2-(x-2)x-2 = -1, яғни

limх--2+x-2x-2 != limх--2-x-2x-2. Олай болса келтірілген теорема бойынша, x-2x-2

функциясының x = 2 нүктеде шегі жоқ.
Ескерту. Гейне бойынша анықталған шектер үшін де жоғарыдағы сияқты біржақты шектер ұғымын анықтауға болады.

Енді y f (x) функциясы X x:x K, ( K 0) жиынында анықталсын.

3-анықтама. Егер кез келген 0 саны бойынша x ( ) теңсіздігін қанағаттандыратын барлық x X үшін f(x) - А теңсіздігі орындалатындай ( ) 0 саны табылса онда f (x) функциясының х-тің -қа ұмтылғанда шегі бар және ол А санына тең дейді де, lim х--infinityfх=А немесе f (x) A (х ) т.с.с. символ- дарының бірімен белгілейді. Бұл жағдайға да біржақты шектер ұғымын келтірейік

3-анықтама. Егер кез келген 0 саны бойынша x () x () теңсіздігін қанағаттандыратын барлық x үшін

f(x) - А

теңсіздігі орындалатындай () 0 саны табылса онда x-тің -қа ( -қа) ұмтылғанда f (х) функциясының шегі бар және ол А санына тең дейді де,
lim х--+infinityfх=А немесе f(х)--А, x--+infinity

(lim х---infinityfх=А немесе f(х)--А, x---infinity)

символдарының бірімен белгілейді.

Теорема. lim х--infinityfх шегі бар болуы үшін lim х--+infinityfх және lim х---infinityfх біржақты шектері бар әрі олардың өзара тең болуы қажетті және жеткілікті яғни

lim х--+infinityfх = lim х---infinityfх=А ⇔ lim х--infinityfх=А.

Дәлелдеуі алдыңғы теорема дәлелдемесі сияқты, жаттығу ретінде дәлелдеп көреміз.
Мысал. Дәлелдеу керек: lim ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.