Осылай құралған декарттық жүйедегі параболаның теңдеуі

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

Жоспар:

І. Кіріспе

ІІ. Негізгі бөлім

Екінші ретті қисықтар
Шеңбер
Элипс
Гипербола
Парабола

ІІІ. Қорытынды

ІV. Пайдаланған әдебиеттер тізімі

Кіріспе

Біздің қарастырайық деп отырған қисық сызықтар осы екінші дәрежелі теңдеудің арнайы түрлермен анықталады. Олар шеңбер, эллипс, гипербола және парабола. Ғылым және техника салаларында осы қисық сызықтар кездеседі. Геометрияда бұл қисық сызықтар теориясын конустық қимылдардың теориясы деп отырған қисық сызықтар қарсы екінші дәрежелі теңдеудіңарнайы түрлерімен анықтлады. Олар шеңбер, эллипс, гипербола және парабола.

Екінші ретті қисықтар

Жоғары математкада екінші дәрежелі теңдеулермен анықталатын сызықтарды екші pеттi қисықтар деп атайды. Олар негізінен шеңбер, эллипс, гипербола және парабола деп аталады. Бұл қисықтар техника мен ғылым саласында иі кездеседі.

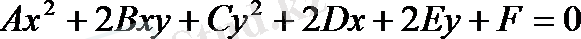
мұндағы 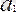, , 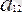, , 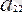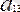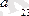- теңдеудің коэффиценттері, 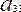- бос мүше, 11, 12, 23, 22, 13, 33- коэффиценттердің индекстері. Екінші ретті сызықтардың жалпы теңдеуі алты мүшеден, яғни екінші дәрежелі үш мүшеден, бірінші дәрежелі екі мүшеден және бос мүшеден құралған.

1-мысал. 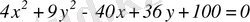теңдеуін канондық түрге келтіру керек.

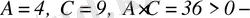эллипстің теңдеуі.

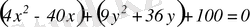
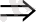
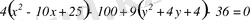
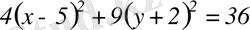
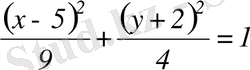. Осыдан 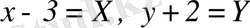деп белгілесек 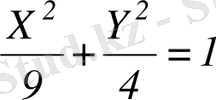-эллипстің канондық теңдеуі, Бұл жүйенің басы 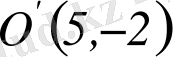нүктесінде орналасқан

Мұндай жалпы теңдеу қандай жағдайда эллипс, гипербола немесе парабола болады? Ол коэффиценттердің мәндеріне байланысты. Мәселен,

1) . Егер = , = , =-1, = = =0 болса, онда + =1 - эллипс:

2) . Егер = , =- , =-1, = = =0 болса, онда екінші ретті сызық - =0 - гипербола:

3) . Егер = = = =0, =1, =-p болса, онда екінші ретті сызық =-2рх - парабола болады.

Коэффиценттердің кейбір мәндерінде екінші ретті сызық басқа геометриялық бейнелерге де ауысуы мүмкін. Мысалы,

1) . Егер =1, =-1, = = = =0 болса, онда - =0, (х+у) (х-у) =0, х+у=0, x-y=0 - екі түзудің теңдеуі:

2) . Егер = = =0, =4, =2, =5 болса, онда 8х+4у+5=0 бір түзуі шығады.

Сонымен, (1) теңдеу коэффиценттерінің мәндеріне байланысты эллипсті, гиперболаны, параболаны немесе басқа геометриялық бейнені (мысалы, түзуді ) көрсетуі мүмкін. Сондықтан бұл теңдеудің координаталар системасындағы геометриялық мағынасын зерттеу үшін оның коэффиценттеріне байланысты қандай болатындығын тексеру керек. Бір тік бұрышты координаталар системасына көшкенде теңдеудің коэффиценттері өзгеріледі. Ал әрбір теңдеу сызықтың координаталар системасында қалай орналасатындығын анықтаумен қатар, оның координаталар системасына тәуелсіз ішкі қасиетін анықтауы да мүмкін. Ендеше, кез-келген тік бұрышты координаталар системасында мәндері өзгерілмей отыратын коэффиценттердің функциялары болуы керек. Ал бір тік бұрышты координаталар системасынан екінші тік бұрышты координаталар системасына көшкенде мәндері сақталатын коэффиценттердің функцияларын инварианттар деп атайды. Басқаша айтқанда, бір системадан екінші системаға көшкенде (1) жалпы теңдеудің коэффиценттерінің мәндері өзгерілмесе (немесе кейбір коэффиценттерінң қосындысы не көбейтіндісі сақталса), ондабұл коэффиценттер инварианттар деп аталады. Сондықтан келесі параграфтарда теңдеудің түрленуін тексерумен қатар, осы инварианттарды да іздеуге кірісеміз. Инвариант деген сөз өзгермейді (сақталады) деген мағына береді.

Шеңбер

Жоғары математикада екінші дәрежелі теңдеулермен анықталатын сызықтарды екінші ретті қисықтар деп атайды. Олардың негізгілері шеңбер, эллипс, гипербола және парабола деп аталады. Екінші ретті беттер деп координаталар жүйесінде екінші дәрежелі теңдеулермен берілетін беттерді айтады.

Центр деп аталатын берілген нүктеден бірдей қашықтықта жататын жазықтықтағы нүктелердің геометриялық орындарын шеңбер деп атайды. Егер r -шеңбердің радиусы болса, ал C(a; b) -оның центрі болса, онда шеңбердің теңдеуі:

(x − a) ² + ( y − b) ² =r ² .

Егер шеңбердің центрі О(0; 0) координаттар басымен сәйкестенсе, онда шеңбердің теңдеуі:

x ² + y ² =r ² .

Жазықтықта M ₁ (x ₁ y ₁ ) нүктесі берілсін. Егер (x ₁ − a) ² + ( y ₁ − b ² ) =r ² , онда M1 шеңбердің бойында жатыр, егер (x ₁ − a) ² + ( y ₁ − b) ² < r ² , онда нүкте шеңбердің ішінде жатыр, егер де (x ₁ − a) ² + ( y ₁ − b) ² > r ² болса, шеңбердің сыртында.

Мысал. 2x2 + 2y2 - 8x + 5y - 4 = 0 теңдеуі арқылы берілген шеңбердің центрінің координаталары мен радиусын тап. .

Шешу. Шеңбердің центрі мен радиусын табу үшін теңдеуді (1) теңдеу түріне келтіріп аламыз. Ол үшін теңдеудің сол жағындағы көпмүшенің толық квадратын бөлеміз.

x2 + y2 - 4x + 2, 5y - 2 = 0

x2 - 4x + 4 -4 + y2 + 2, 5y + 25/16 - 25/16 - 2 = 0

(x - 2) 2 + (y + 5/4) 2 - 25/16 - 6 = 0

(x - 2) 2 + (y + 5/4) 2 = 121/16

Бұл теңдеуден мынаны табамыз: О(2; -5/4) ; R = 11/4.

Эллипс

Белгіленіп алынған F1 және F2 нүктелеріне дейінгі қашықтарының қосындысы тұрақты шама болатын М нүктелерінің геометриялық орыны эллипс деп аталады. F1, F2 нүктелері эллипстің фокустары деп аталады. Осы анықтама бойынша, эллипстің бойындағы М нүктелері үшін F1M + F2M =2a (1) теңдігі орындалады және эллипсті төмендегі ретпен салуға болады: үштары F1 және F2 нүктелерінде бекітілген, ұзындығы 2а-ға тең созылмайтын жіпті қарындаштың үшінен тартып қозғасақ, оның үші эллипсті сызып шығады. (1 сурет) .

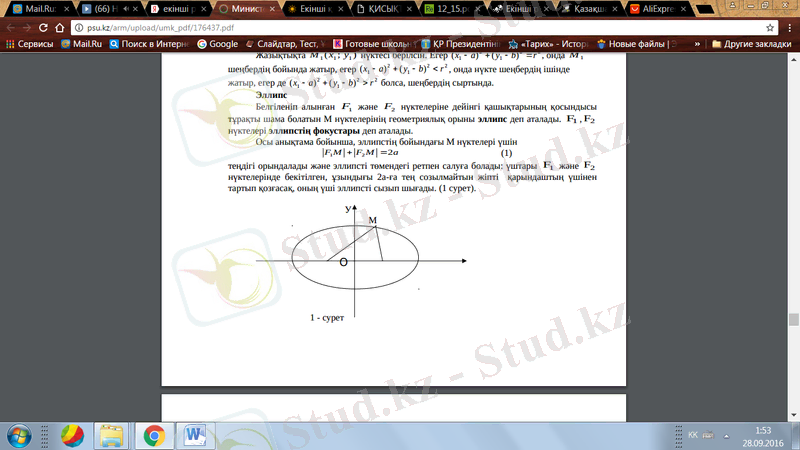
Эллипсті нүктелері арқылы салу әдісі:

1) радиустары а және b-ға тең центрлес екі шеңбер сызылады (b < a ) ;

2) Осы шеңберлердің ортақ центрі О нүктесінен Ох өсінің оң бағытымен t бұрышын

жасайтын сәуле жүргізіледі. Бұл сәуле ішкі шеңберді Q нүктесінде сыртқы шеңберді Р

нүктесінде қиып өтеді;

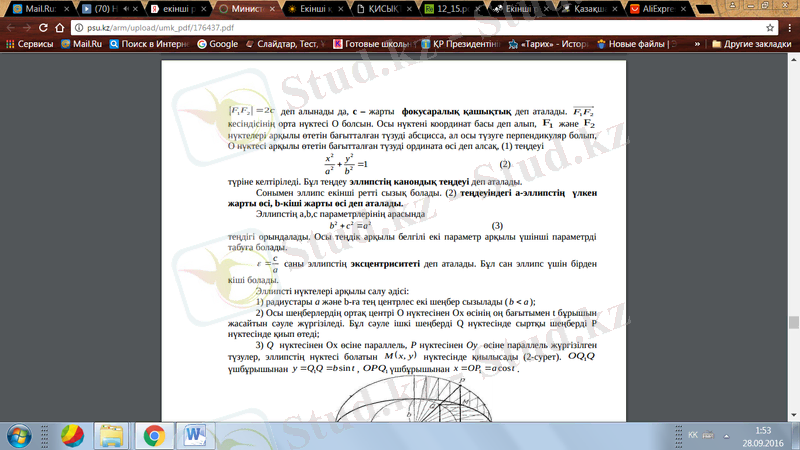
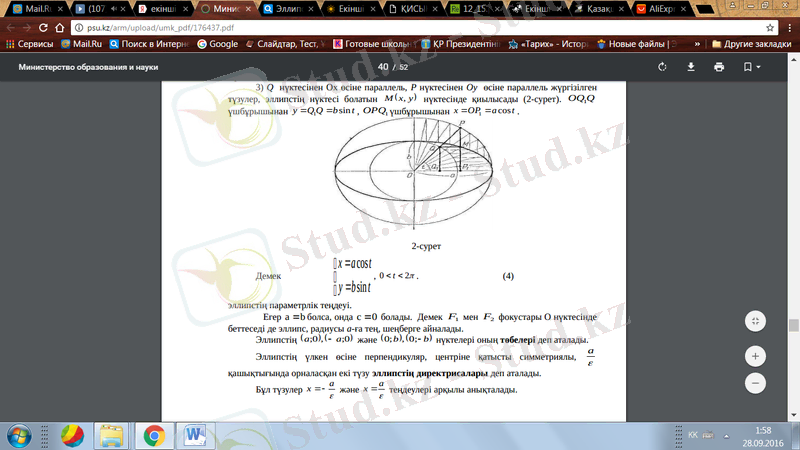
3) Q нүктесінен Ох өсіне параллель, Р нүктесінен Оу өсіне параллель жүргізілген

түзулер, эллипстің нүктесі болатын M ( x, y) нүктесінде қиылысады (2-сурет) . OQ1Q

үшбұрышынан y=Q ₁ Q= bsin t, OPQ1 үшбұрышынан x OP a cost

Теорема 1 Егер эллипстің кез келген М нүктесінен оның екі фокусының біреуіне дейінгі қашықтық r болып, осы фокус жағындағы директрисаға дейінгі қашықтық d болса, онда r /d эллипстің эксцентриситетіне тең тұрақты шама болады: ε= r/ d .

Мысалдар:

1) 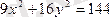эллипсі берілген. Оның параметрлік теңдеулерін жазу керек.

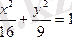
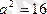
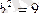
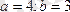
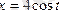
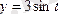2) Эллипстің 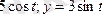параметрлік теңдеулері берілген. Оның канондық теңдеуін жазу керек.

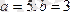
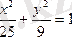
3) Фокальдық қашықтығы 6-ға тең болғандағы М(5; 0) нүктесі арқылы өтетін эллипстің канондық теңдеуін жазу керек.

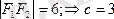
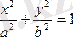
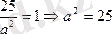
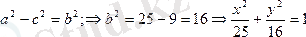
4) 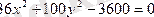теңдеуі эллипстің теңдеуі екенін дәлелдеу керек.

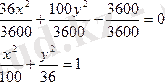
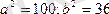
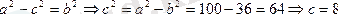
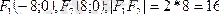
Гипербола

Фокустары деп аталатын, белгіленіп алынған F1 және F2 нүктелеріне дейінгі қашықтықтарының айырымы тұрақты шама болатын М нүктелерінің геометриялық орыны гипербола деп аталады. Аталған айырымның абсолют шамасы 2а деп белгіленеді және бұл шама фокустар арасындағы қашықтықтан кіші болады. Демек, егер F1F2 =2c болса, a < c болады.

Сонымен, анықтама бойынша, егер М нүктесі F1 фокусына жақын орналасса

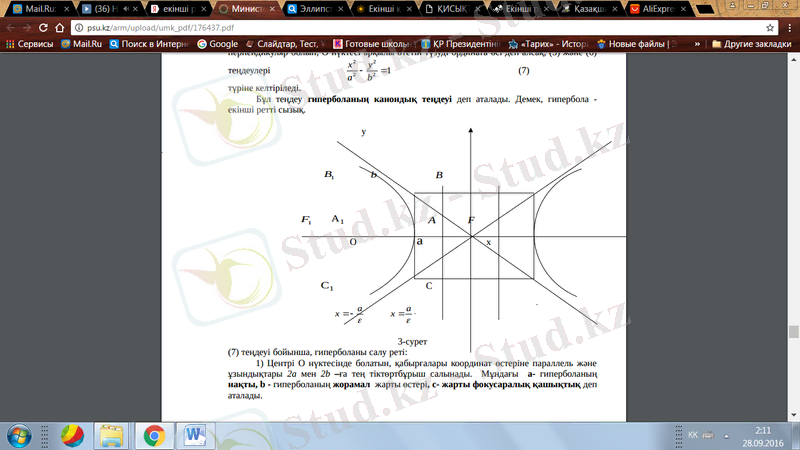
F1F2 кесіндісінің орта нүктесі О болсын. Осы нүктені координат басы деп алып, F1 және F2 нүктелері арқылы өтетін бағытталған түзуді абсцисса, ал осы түзуге перпендикуляр болып, О нүктесі арқылы өтетін түзуді ордината өсі деп алсақ, (5) және (6) теңдеулері

түріне келтіріледі.

Бұл теңдеу гиперболаның канондық теңдеуі деп аталады. Демек, гипербола - екінші ретті сызық.

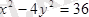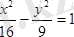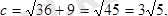
Мысал. теңдеуімен берілген гипербола (а, 6, с, е) параметрлерін табу кенрек. Ол үшін берілген теңдеуді канондық түріне келтіреміз. Бұдан а = 6, b = 3 болатыны шығад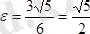ы, . лы 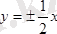гипербола асимптотасының теңдеуі

қашықтығы d болса, онда d r гиперболаның эксцентриситетіне тең тұрақты шама болады: ε = r /d .

Парабола

Фокус деп аталатын, белгіленіп алынған F нүктесі мен директриса деп аталатын l түзуіне дейінгі қашықтықтары өзара тең болатын нүктелердің геометриялық орны парабола деп аталады. (5-сурет)

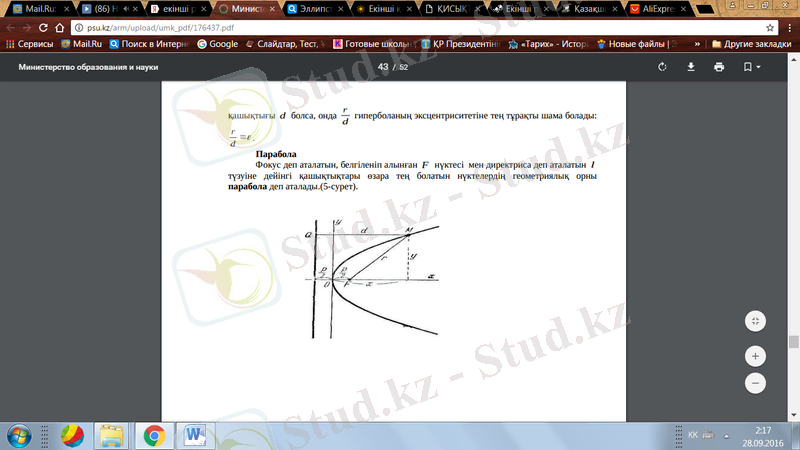5-cурет

Параболаның директрисасынан фокусына дейінгі қашықтығы р оның параметрі деп аталады.

Тікбұрышты декарттық жүйенің абсцисса өсі директрисаға перпендикуляр болып параболаның фокусы арқылы, ал ордината осі директриса мен фокусты жалғастыратын кесіндінің орта нүктесі арқылы өтсін.

Осылай құралған декарттық жүйедегі параболаның теңдеуі

У ² =2РХ

Бұл теңдеу де екінші дәрежелі. Сондықтан, парабола екінші ретті сызық.

Параболаның қасиеттері:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.