Ақырғы өлшемді кеңістіктегі сызықты оператордың меншікті мәні мен меншікті векторы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 19 бет
Таңдаулыға:

КІРІСПЕ

Функионалды анализ - топологиялық векторлы кеңістіктер анализы, және олардың бейнелеулері. Функционалды анализ бөлімінде ішінара тағы да бөлімшелерге бөлінген оларға: өлшем теориялары, интегралдар теориясы, функция теориясы, операторлар теориясы, дифференциалды талдау. Функционалды анализ методикалары көптеген нақты ғылымдар арасында қолданылатын орны ерекше, мысалы физика, химия, алгебра және тағы басқа. Оның негіздерімен дифференциалдық теңдеулер тоериясында, математикалық физикада, теориялық физикада, кванттық механикада, жолдар теориясында және басқа да ғылым салаларымнда қолданылады. Функционалды анализды зерттеу барысында үлкен үлес қоскан Фурье қатарына түрлендіруі. Сол түрлендіру негізінде функционалды анализдың анықтамалары құрылды.
Қазіргі заманғы функционалды анализ бірнеше бөлімдерге бөлінеді: сызықты емес функционалды анализ - деформация, бифуракцияларды зерттеу; жұмсақ анализ (талдау) - топологиялық жүйелерде құрылған; бейнелеу теориясы - кванттық механикамен жиынтығындағы анализ; Банахтық кеңістіктер геометриясы; кванттық функионалды анализ - операциялық бірліктер кеңістігін зеррттеу; коммутативты емес геометрия - Ален Конн еңгізген, эргодикалық теорияны қолданатын анализ.
Операторлар теориясы функционалдық талдау бөлімі болып табылады, ол қалыпты кеңістіктер арасындағы үздіксіз сызықтық салыстырулардың қасиеттерін зерттейді. Жалпы айтқанда, оператор - соңғы өлшемді кеңістіктегі қарапайым функция немесе матрицаның аналогы. Бірақ оператор шексіз өлшемді кеңістікте әрекет ете алады.
Сызықтық трансформация - олардың сызықтық құрылымдарымен сәйкес келетін екі векторлық кеңістік арасындағы салыстыру.
Сызықтық оператор векторлық кеңістіктің тұжырымдамасымен қатар сызықты алгебрадағы басты тұжырымдамасы математика мен физикадағы ең алуан түрлі салаларда, бірінші кезекте, талдау және оны қолдануда маңызды рөл атқарады.
Сызықтық оператор қазіргі заманғы анықтамасын алдымен J, Peano берді. Дегенмен, математиканың алдыңғы дамуы, ол жинақталған (сызықтық функциядан бастап y = ax) бастап дайындалды.
Меншікті векторлар - олардың координат жүйесінде, матрицада сипатталған зат ең тартымды көрінеді.
Жалпы алғанда, барлық негізгі процестер белгілі бір мағынада сызықты, сондықтан сызықтық операторлардың теориясы өте маңызды. Сызықты картография не істейді? Жалпы мағынада ол параллель жылжиды және созылады (немесе қысылады). Бұл ретте, желілік оператордың өз векторлары шын мәнінде дифференциалдық теңдеулер бастап сандық әдістерге дейінгі көптеген облыстарда өте қызықты және маңызды қосымшалары бар деп аталатын қозғалмайтын нүктелер болып табылады.
Жеке мағынада, меншікті векторлар, кез-келген қозғалмайтын нүкте сияқты, іс жүзінде ағып жатыр, айналасында орналасқан барлық басқа нүктелердің тартылғанын көрсетеді.
Меншік мәндер жиі сызықтық алгебра немесе матрицалық теория тұрғысынан енгізіледі. Дегенмен, тарихи түрде, олар төртбұрыш нысандарын және айырымдық теңдеулерді зерттеуде пайда болды.
XVIII-ші ғасырда Эйлер қатты айналмалы қозғалысты зерттеді және негізгі осьтердің маңыздылығын анықтады. Лагранж негізгі осьтер инерция матрицасының өздік векторы екенін түсінді.
XIX ғасырдың басында Коши өздерінің жұмысын екінші реттік беттерді классификациялауға және еркін өлшемдерге жалпылауға қалай қолданатынын көрді. Коши, сондай-ақ, қазір өздігінен мән деп аталатын Racine caractéristique (сипаттамалық түбір) терминін құрастырды; оның термині тән теңдеулерінде өмір сүреді.
Фурье Лаплас пен Лагранжтың жұмысын пайдаланып, 1822 жылғы Théorie analytique de la chaleur әйгілі айнымалы мәндерін бөлу арқылы жылулық теңдеуді шешеді.
Штурм Фурьенің идеяларын әрі қарай дамытты және оларды өз идеяларымен біріктіріп, нақты симметриялық матрицаның шын мәнінде меншікті мәні бар екеніне қол жеткізген Кошидің назарына жеткізді. 1855 жылы Хермита кеңейтіп, енді Эрмит матрицасы деп аталады.
Сонымен қатар, Бриокки дәлелдеді, ортогоналды матрицаның өз мәндері бірлік шеңберіне жатады, ал Клебш анықталғандай, ауытқуларға сәйкес нәтиже симметриялық матрицалар болып табылады. Ақырында, Вейерштрасс басталған тұрақтылық теориясының маңызды аспектісін түсіндірді, бұл ақаулы матрицаның тұрақсыздыққа әкелуі мүмкін екенін түсінді.
Дегенмен, Лювилль Штурм сияқты өзіндік құндылық мәселелерін зерттеді, олардың жұмысынан пайда болған тәртіп қазіргі уақытта Штурм-Лиувилл теориясы деп аталады. Шварц XIX -шы ғасырдың аяғында жалпы домендердегі Лаплас теңдеуінің алғашқы меншікті мәнін зерттеді, ал Пуанкаре Пуассон теңдеуін бірнеше жылдан кейін оқыды.
ХХ ғасырдың басында Гильберт композит операторларының өз мәндерін зерттеді, операторларды шексіз матрицалар деп қарастырады. Ол 1904 жылы өзінің меншікті мәндері мен меншікті векторларын білдіретін меншікті дегенді білдіретін неміс сөзін өздігінен бірінші болып қолданған, бірақ ол Гельмгольцті қолдануға қатысты болуы мүмкін.
Біраз уақыттан бергі ағылшын тіліндегі стандартты термин өзіндік құндылық болды, бірақ меншікті құндылық термині бүгінгі күні стандартты болып табылады.
Алғашқы сандық есептеу алгоритмі 1929 жылы пайда болған кезде, электронды әдісті жариялаған Вон Мизз пайда болды. Бүгінгі таңда ең танымал әдістердің бірі QR алгоритмі Джон Г.Ф. өз бетімен ұсынылды. Френсис және Вера Кубановская 1961 жылы.
І СЫЗЫҚТЫ АЛГЕБРА

Сызықтық алгебра - алгебраның есептердің сандық шешімдерін математикалық бейнелеу және зерттеу процестеріне арналған маңызды бөлімі. Сызықтық алгебраның негізгі есептерінің екеуінің мәні ерекше зор: сызықтық алгебралық теңдеулер жүйесінің шешімі және матрицаның меншікті мәні мен меншікті векторларын анықтау. Басқа да жиі кездесетін есептері: кері матрицаны табу, анықтауышты есептеу, алгебралық көпмүшеліктің түбірін табу. Сызықтық теңдеулер теориясы - сызықтық алгебраның ең алғашқы саласы. Бұл теорияның дамуы нәтижесінде анықтауыштар теориясы, одан кейін матрицалар теориясы және бұған байланысты векторлық кеңістіктер мен сызықтық түрлендірулер теориясы жасалды. Сызықтық алгебраға, сондай-ақ формалар теориясы, оның ішінде квадраттық формалар және ішінара инварианттар теориясы мен тензорлық есептеулер де енеді. Функционалдық анализдің кейбір тараулары сызықтық алгебраның осыған сәйкес мәселелерінің одан әрі дамуы болып есептеледі.

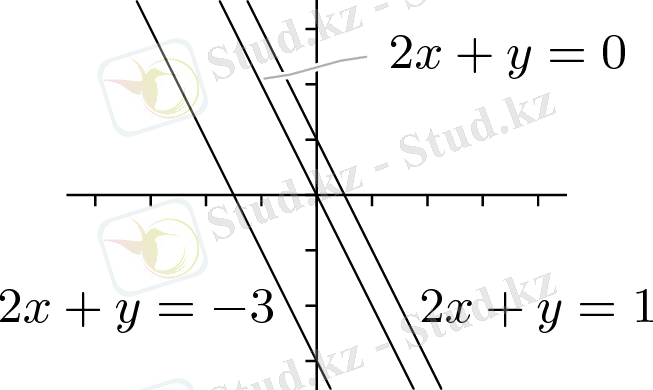
1-сурет

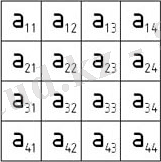
2-сурет

Матрица деп m қатар және n бағаннан тұратын тікбұрышты кестеде орналасқан m n сандар (нақты немесе комплексті) жүйесіне айтамыз. (2) суретте қатар және бағандары матрицаның қатарлары мен бағандары деп аталады. Берілген матрицаны құрайтын aij(i=1,2,...,m; j=1,2,...,n) сандар оның элементтері деп аталады. Бұл жердегі бірінші i индексі қатар элементі номерін, ал екінші j-оның баған номерін білдіреді. Матрица үшін мына қысқартылған жазу жиі қолданылады. A=[aij] (i=1,2,...,m; j=1,2,...,n) немесе A=[aij]m,n, сонымен бірге А матрица m x n түрге ие деп аталады.
Егер m=n болса, онда матрица n ретті квадраттық деп аталады. Егер де m!=n болса, онда матрица тікбұрышты деп аталады. Дербес жағдайда, 1 x n түрдегі матрица ветор-қатар деп, ал m x 1 түрдегі матрица вектор-баған деп аталады. Сан(скаляр)ды 1 х 1 түрдегі матрица деп қарастыруға болады. Төмендегідей түрдегі квадраттық матрица диогональдық деп аталады да қысқаша [α1, α2,..., αn] деп жазылады. Егер αi=1(i=1,2,...,n) жағдай болатын болса, онда (2) матрица бірлік матрица деп аталады және әдетте Е әрпімен белгіленеді, яғни кронекер Паскаль символын енгізіп 0, егер і!=j болса, 1, егер і=j болса, Е = [ δi j] жазуға болады.
Барлық элементтері нольге тең матрица нольдік матрица деп аталады және 0 арқылы белгіленеді. Егер нольдік матрицаның тағы да қатар және баған сандарын көрсетпекші болса, онда 0mn , белгісін қолданады.
А= [ai j] n,n квадраттық матрицасымен анықтауышы(детерминанты) байланысқан. Бұл екі ұғымды бірдей мағынада теңестіруге болмайды. Матрица өздігінен сандардың тікбұрышты кесте түрінде жазылған, реттелген жүйесін береді, ал оның det A анықтауышы белгілі ереже бойынша анықталатын сан болады, атап айтқанда

Det A= (α1,α2,...,αn)(-1)tα1α1,α2α2,...,αn αn (1.1)

Мұндағы (1.1) сумма 1,2,...,n элементтердің (α1, α2,..., αn) мүмкін болған барша орналастыруы болады, демек, n! қосылғышқа ие, сонымен бірге μ=0 болады, егер орналастыру жұп болса, және μ=1 болады, егер орналастыру тақ болса.

1.1 Вектор ұғымына түсінік

Бағытталған кесінді AB A B -- {\displaystyle {\overrightarrow {AB}}} деп A {\displaystyle A} A -- "бас нүктесінен" бастап екінші B {\displaystyle B} B- "соңғы"нүктесіне дейінгі түзу бойындағы нүктелер жиыны.
Жәй мағынасына сәйкес вектор деп бағытталғын кесінді деп түсінуге болады, ал басқа жағдайларда әртүрлі векторлар - белгілі бір эквиваленттік қатынасы бойынша әртүрлі бағытталған кесінділер эквивалентті класстары болып табылады. Бұл эквиваленттік қатынасы әртүрлі болуы мүмкін: ол векторлардың түрін анықтайды ("еркін", "тұрақты" т.б.). Басқаша айтқанда, эквивалентті класс ішінде кез келген екі вектор тең болып есептеледі, яғни кез келген вектор сол класты толықтай бейнелей алады.
Еркін векторлар жиыны мен олардың кеңістікті параллель жылжыту жиыны арасындағы изоморфизмды ескерсе, егерде қосу операциясын жылжыту композицияларымен теңестірсе, онда кеңістікті параллель жылжыту жиынын тіпті векторды анықтау үшін де пайдалануғы болады.
Кеңістікті шексіз аз трансформацияларын зерттеуде маңызды рөл атқарады.
* Бaс нүктесі соңғы нүктесімен беттесетін векторды нөлдік вектор деп атайды: A A -- = 0 -- . {\displaystyle {\overrightarrow {AA}}={\vec {\mathbf {0} }}.} AA=0
* B A -- {\displaystyle {\overrightarrow {BA}}} BA векторын A B -- {\displaystyle {\overrightarrow {AB}}} AB векторына қарсы вектор деп атайды.

Еркін, сырғанақ және тұрақты векторлар

Кейде, векторлар ретінде "барлық" тең бағытталған кесінділер жиыны орнына осы жиынның әлдебір өзгертілген түрін (факторжиынын) айтады. Осылайша еркін (барлық ұзындықтары мен бағыттары бірдей векторларды бір (толықтай бірдей) деп қарастырады), сырғанақ (еркін мағынасы байынша тең векторларды егер бас нүктелері мен соңғы нүктелері бір түзудің бойында жатса) және тұрақты векторлар (іс жүзінде бағытталған кесінділердің бас нүктелері әр-түрлі болса - векторлар тең емес деген сөз).
Анықтама. Еркін ABA B -- {\displaystyle {\overrightarrow {AB}}} мен CD C D -- {\displaystyle \ {\overrightarrow {CD}}} векторлары, егер төртбұрыш ABFEA B F E {\displaystyle ABFE} мен CDFE C D F E {\displaystyle CDFE} CDFEC -- параллелограмм болатындай EE {\displaystyle E} және F F {\displaystyle F} FFFF нүктелері табылса, тең болады.
Ескерту. Анықтаманың күрделенген себебі - A , B , C , D {\displaystyle A,B,C,D} A,A,B,C,D нүктелерінің бір түзу бойында жату мүмкіндігінен. Әйтпегенде, оны оңайырақ былай жазуға болар еді:
Анықтама. Еркін бір түзу бойында жатпайтын A B -- {\displaystyle {\overrightarrow {AB}}} ABжәне C D -- {\displaystyle \ {\overrightarrow {CD}}}CD C D -- {\displaystyle \ {\overrightarrow {CD}}} векторлары, егер төртбұрыш ABCD A B D C {\displaystyle ABDC} -- параллелограмм болса, тең болады.
Анықтама. Сырғанақ AB A B -- {\displaystyle {\overrightarrow {AB}}} және CD C D -- {\displaystyle \ {\overrightarrow {CD}}} C D -- {\displaystyle \ {\overrightarrow {CD}}} векторлары, егер * A , B , C , D {\displaystyle A,B,C,D} A,B,C,D нүктелері бір түзу бойында жатпаса, ал * AB A B -- {\displaystyle {\overrightarrow {AB}}} A B -- {\displaystyle {\overrightarrow {AB}}} мен CD C D -- {\displaystyle \ {\overrightarrow {CD}}} C D -- {\displaystyle \ {\overrightarrow {CD}}} C D -- {\displaystyle \ {\overrightarrow {CD}}} векторлары еркін векторлары ретінде тең болса, онда оларда өзара тең деп аталады. Қарапайым сөзбен айтқанда, сырғанақ векторларға бағыты мен ұзындығын өзгертпей түзуінің бойымен қозғалуына рұқсат етілген.
Ескерту. Сырғанақ векторлар әсіресе механикада пайдаланылады. Механикадағы ең қарапайым мысал -- күш. Өзі жатқан түзу бойымен вектор бас нүктесін көшіргенмен қай нүктеге қатысты есептесе де күш моменті өзгермейді; керісінше, басын басқа түзуге көшірсе тіпті вектордың бығыты мен ұзындығын сақтағанның өзінде күш моменті әрдайым дерлік өзгереді: сондықтан күшті еркін вектор ретінде санауға болмайды.
Анықтама. Егер сәйкесінше A A {\displaystyle A} мен C C {\displaystyle C} , B B {\displaystyle B} мен D D {\displaystyle D} нүктелері беттессе, онда тұрақты AB A B -- {\displaystyle {\overrightarrow {AB}}} A B -- {\displaystyle {\overrightarrow {AB}}} және CD C D -- {\displaystyle \ {\overrightarrow {CD}}} C D -- {\displaystyle \ {\overrightarrow {CD}}} C D -- {\displaystyle \ {\overrightarrow {CD}}} векторлары тең деп есептеледі.

Векторларды қосу

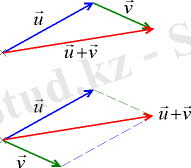
3-сурет

Екі u, v векторлары және олардың қосындысы

Екі векторларды қосуды параллелограмм ережесімен де, үшбұрыш ережесімен де іске асыруға болады.
Үшбұрыш ережесі. Екі u мен vv -- {\displaystyle {\vec {v}}} векторларын үшбұрыш ережесімен қосу үшін осы екі векторды өздеріне біреуінің бас жағы екіншісінің аяғымен беттесетіндей параллель көшіру керек. Сонда пайда болған үшбұрыштың үшінші қабырғасы бас жағы алғашқы вектордың басымен беттесетін бастапқы екі вектордың қосынды векторы болып табылады.
Параллелограмм ережесі. Екі u u -- {\displaystyle {\vec {u}}} мен v v -- {\displaystyle {\vec {v}}} векторларын параллелограмм ережесімен қосу үшін екеуін де бастары беттесетіндей параллель көшіріп параллелограммға болықтырады. Сонда екеуінің қосындысы деп параллелограммның осы екі вектор бас жағынан шығатын диагоналін айтады.
Екі сырғанақ векторларды қосу тек қана олар жатқан екі түзу қиылысқанда ғана анықталған. Бұл жағдайда әр вектор өз түзуі бойымен қиылысу нүктесіне дейін көшіріліп, содан кейін параллелограмм ережесімен қосылады.
Екі тұрақты векторларды қосу тек егер олардың ортақ бас нүктесі болғанда ғана анықталған. Бұл жағдайда да олар параллелограмм ережесімен қосылады.

Коллинеар сырғанақ векторларды қосу

Егер екі сырғанақ векторлар параллель болса, онда қосындыны табу қиыншылығы қосынды вектор жатқан түзуді табудың қиындығында жатыр. (Қосынды вектор бағыты мен ұзындығын еркін векторларды қосқандағыдай анықтаған абзал болар еді) механикада статиканы зерттегенде параллель, еркін векторлармен берілетін, күштерді қосу мәселесінде қосымша гипотеза беріледі: берілген векторлар жүйесіне осы векторлар жатқан түзулерді қиып өтетіндей ұзындықтары бірдей, бағыттары қарама-қарсы бір түзу бойында жататындай екі векторды қосуға болады. Мысалы, параллель түзулерде жататын сырғанақ екі a және b вeкторларын қосу керек болсын. Оларға бір түзу бойындағы c мен -c векторларын қосайық. a мен c векторлары жатқан түзулер қиылысады, сондықтан a a -- {\displaystyle {\vec {a}}} мен -c − c -- {\displaystyle -{\vec {c}}} векторлары да қиылысады. Яғни, келесі векторлар анықталған a,=a+c, b,=b-c. a, мен b, векторлары жатқан түзулер a мен b векторлары шамалы бойынша тең бірақ бағыттары қарама-қарсы болғанда ғана қиылыспайды, бұл жағдайда a мен -a векторлары - векторлар жұбы деп аталады.
Сонымен қорыта айтса, a және b векторларының қосындысы деп a, мен b, векторларының қосындысын түсіну керек және бұл қосынды a мен b векторлары жұп болмаған жағдайдың бәрінде дұрыс анықталған.

Векторларды санға көбейту

a a -- {\displaystyle {\vec {a}}} векторы мен λλ {\displaystyle \lambda } санының көбейтіндісі λa λ a -- {\displaystyle \lambda {\vec {a}}} деп a -- λ {\displaystyle {\vec {a}}\lambda } белгіленетін, модулі λ ⋅ a -- {\displaystyle \lambda \cdot {\vec {a}}} λ∙aтең, ал бағыты a a -- {\displaystyle {\vec {a}}} векторының бағытымен бірдей, егер λ 0 {\displaystyle \lambda 0\,} 𝜆0λ 0 {\displaystyle \lambda 0\,} болса, және керісінше, қарсы бағытталады, егер 𝜆0λ 0 {\displaystyle \lambda 0\,} болса. Егер λ = 0 {\displaystyle \lambda =0\,} λλ=0, немесе вектор a a -- {\displaystyle {\vec {a}}} нөлдік болса, тек осы жағдайда ғана көбейтінді де λ a -- {\displaystyle \lambda {\vec {a}}} λa -- нөлдік вектор. Әдетте бұл көбейтіндіні жазғанда бірінші санды сосын векторды жазады, дегенмен де керісінше жазу да қате емес. Қалай десек те, λa=aλ λ a -- = a -- λ {\displaystyle \lambda {\vec {a}}={\vec {a}}\lambda } .
Скаляр көбейтіндісі
Аңықтама. a және b векторларының (a, b) скаляр көбейтіндісі деп ax· bx + ay· by саның атаймыз:
(a, b) = ax · bx+ay · by (1.2)
Мысалы a = {1, 3}, b = {4, 2} болса, онда (a, b) = 1·4+3·2 = 4+6 = 10.
Скаляр көбейтіндінің қасиеттері:
1). (a, b) = (b, a)
2). (a, a) = a2
3). (a+b, c) = (a, c) + (b, c)
4). (a - b, c) = (a, c) -(b, c)
5). (k ·a, b) = (a, k ·b)=k ·(a, b) (1.3)

Геометриялық түрде алғанда скаляр көбейтінді бір вектордың ұзындығын екінші вектордың біріншісінің бағытына ортогональ проекциясының ұзындығын көбейткенге тең. Кез келген a a -- {\displaystyle {\vec {a}}} векторының бірлік вектормен скаляр көбейтіндісі a -- {\displaystyle {\vec {a}}} a векторының сол бірлік векторға ортогональ проекциясы болып табылады.

Векторлық көбейтінді

a векторынының b векторына Векторлық көбейтіндісі деп келесі шартты қанағаттандыратын c векторын айтады: c векторының ұзындығы a мен b векторларының ұзындықтарының және осы векторлардың арасындағы φ бұрышының синусының көбейтінділеріне тең:
c -- = a -- b -- sin ⁡ ϕ {\displaystyle \left{\vec {c}}\right=\left{\vec {a}}\right\left{\vec {b}}\right\sin \phi } c=absinφ c векторы a мен b векторларының әр-қайсысына ортогональ; c векотры abc үштігі оң болатындай бағытталған.
Белгілеулер: c -- = [ a -- b -- ] = [ a -- , b -- ] = a -- x b -- {\displaystyle {\vec {c}}=\left[{\vec {a}}{\vec {b}}\right]=\left[{\vec {a}},{\vec {b}}\right]={\vec {a}}\times {\vec {b}}} c=ab=a,b=axb
Геометриялық мағынасы бойынша axb a -- x b -- {\displaystyle {\vec {a}}\times {\vec {b}}} векторлық көбейтіндісі a,b a -- , b -- ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.