Параметрге тәуелді теңдеулердің теориясы және шешу әдістері


Курстық жұмыс
«Параметрге тәуелді теңеулер»
МАЗМҰНЫ
КІРІСПЕ . . . 3
І Құрамында параметрге тәуелді теңдеулердің теориялық негіздері
1. 1 Параметр түсінігі. Құрамында параметрі бар теңдеулердің
түрлері . . . 4
1. 2 Құрамында параметрі бар квадраттық теңдеулер . . . 8
ІІ Параметрге тәуелді теңдеулерді шешудің әдіс-тәсілдері
2. 1 Параметр қатысқан сызықтық теңдеулерді аналитикалық және графиктік жолдармен шешу . . . 13
2. 2 Параметрі бар тригонометриялық теңдеулерді шешу. 20
ҚОРЫТЫНДЫ . . . 26
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . . 27
КІРІСПЕ
Параметрлермен мәселелер логикалық ойлауды, студенттердің математикалық мәдениетін қалыптастыруда маңызды рөл атқарады, бірақ оларды шешу айтарлықтай қиындықтар тудырады. Бұл олардың математика курсының жеке құрамдас бөлігі емес екендігімен түсіндіріледі және негізінен факультативті сыныптарда терең қарастырылады.
Мектептің оқушылары үшін параметрлермен тапсырмалар ерекше болып табылады, олардың көпшілігі күрделі. Формулаларды механикалық қолданудың жеткіліксіздігі, нысанның белгілі бір жалпы қасиеттері, жүйе мен шешімнің реттілігі негізінде белгілі бір жағдайды талдауға арналған үлгілерді, дағдыларды түсіну қажет.
Тақырыптың өзектілігі соңғы жылдарда параметрлері бар мәселелер USE және GIA міндеттерінде үнемі кездеседі. Осылайша, әртүрлі мәселелерді параметрлермен шешу әдістерін әзірлеу қажет екені анық.
Мақсаты: құрамында параметрі теңдеулерді шешу әдістемесін жасау болып табылады.
Міндеттері:
- «параметр» тұжырымдамасын енгізудің барлық мүмкіндігін қарастыруға болады, бұл үшін қолданыстағы оқулықтарды талдау қажет;
- мектептің оқу жоспарында анықталған параметрлермен теңдеулердің негізгі түрлерін анықтаңыз;
-параметрді қамтитын теңдеулерді шешудің неғұрлым ұтымды әдісін әзірлеу.
І Құрамында параметрге тәуелді теңдеулердің теориялық негіздері
1. 1 Параметр түсінігі. Құрамында параметрі бар теңдеулердің түрлері
Алғаш рет «параметр» тұжырымдамасымен 7-ші сыныпта сызықтық теңдеулерді зерттеу кезінде үйренген дұрыс, себебі жоғарғы сыныпқа барғанда осы тақырыпта қиындықтарға кезікпеу үшін. Сонымен қатар, параметрлері бар тапсырмалар логикалық ойлауды жақсы дамытып, есте сақтау мен жадыға үйретеді.
Параметрлік теңдеулерде қолдануға келесі ғылыми-зерттеу дағдыларын бөлуге болады:
1. Параметр арқылы параметрі бар теңдеулердің қай классқа жататындығын анықтау мүмкіндігі;
2. Теңдеудің түрін және параметрге байланысты коэфицент типін анықтау мүмкіндігі;
3. Параметрге тәуелді теңдеулердің шешімдерін параметріне байланысты анықтау;
Параметр - математикадағы (грек параметрінен - өлшеулерден), сандық мәндер бірдей элементтердің жиынтығынан белгілі бір элементті таңдауға мүмкіндік беретін мән.
Теңдеу дегеніміз құрамында мәнін табу керек болатын әрпі бар теңдік. Теңдеуді шешу дегеніміз оның барлық түбірлерін табу немесе оның бірден- бір түбірі болмайтынына көз жеткізу. Теңдеуді тура санды теңдікке айналдыратын әріптің мәні теңдедің түбірі деп аталады.
Мысалы, 7x+5=26 -теңдеу
x=3
3- саны теңдеудің түбірі.
Теңдеулер
Теңдеу деп белгісіз айнымалысы бар алгебралық өрнекті атаймыз. Теңдеулердің түрлері сан алуан- сызықты, квадраттық, тригонометрикалық, логарифмдік және тағы да сол сияқты.
Осы сайтта мынандай теңдеулер мен олардың шешімдері келтірілген:
1. Сызықты теңдеу.
Сызықты теңдеу деп a·x+b=c типті теңдеуді атайды, мұндағы a, b, c тұрақты сандар ал x ізделінетің белгісіз.
2. Сызықты теңдеулер жүйесі.
Мына жүйені сызықты теңдеулер жүйесі деп атайды:
мұндағы x пен y ізделінетін белгісіздер, ал
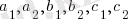 белгілі тұрақты сандар.
белгілі тұрақты сандар.
Сызықтық теңдеу - белгісіздері (айнымалы шамалары) 1-дәрежелі болып келетін және белгісіздердің көбейтінділері қатыспайтын теңдеу. Мысалы,
а 1 х 1 + а 2 х 2 +…+ + а n х n = b (1)
түріндегі теңдеу n белгісізі ( аі≤0, і=1, 2, …, n ) бар сызықтық теңдеуге жатады. Егер (1) теңдеудегі а i =0 (і=2, 3, …, n ) болып, бірақ а1≤0 болса, онда ол а 1 х = b немесе ах = b ( а 1 = а ) түріндегі бір белгісізі бар сызықтық теңдеуге айналады. Берілген айнымалыларға қатысты бірнеше сызықтық теңдеулер жиынтығы Сызықтық теңдеулер жүйесін құрады:
a
11
x
1
+ a
12
x
2
+…+ a
1n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+…+ a
2n
x
n
= b
2
(2)
.
a
m1
x
1
+ a
m2
x
2
+…+ a
mn
x
n
= b
m
Бұл жүйенің теңдеулеріндегі x 1 , x 2 , …, x n белгісіздерінің орнына табылған мәндерін қойғанда сол теңдеулерді тепе-теңдікке айналдыратын а 1 , а 2 , …, а n сандар жиынтығы сызықтық теңдеулер жүйесінің шешімдері деп аталады. Ал сызықтық теңдеулер жүйесі негізгі матрица мен кеңейтілген матрицаның рангілерін салыстыру арқылы шешіледі. Егер олардың рангілері бір-бірімен дәл келсе, онда сызықтық теңдеулер жүйесі үйлесімді, ал кеңейтілген матрицаның рангісі негізгі матрицаның рангісінен үлкен болса, онда сызықтық теңдеулер жүйесі үйлесімсіз болады. Егер сызықтық теңдеулер жүйесінің барлық b i мүшелері нөлге тең болса, онда сызықтық теңдеулер жүйесі біртекті деп аталады. Сызықтық теңдеулер жүйесінің бір шешімі, шексіз көп шешімі немесе мүлде шешімі болмауы да мүмкін. 1-дәрежелі теңдеуді шешу Хорезми еңбектерінде кездеседі. 1750 ж. швейцарлық ғалым Г. Крамер (1704 - 1752) сызықтық теңдеулер жүйесін шешетін ереже тапты, ал 100 жылдан кейін неміс математигі Л. Кронекер (1823 - 1891) бұл теорияны жалпылап, аяқтады.
Сызықтық программалау есебінің стандарт, канондық және жалпы түрлері немесе минималды мән қабылдаса, онда ол оптималды (тиімді) жоспар деп аталады. Егер шектеулер жүйесі тек теңсіздіктерден тұратын болса, онда сызықтық бағдарламалау есебінің мұндай түрі стандартты ( симметриялық ) деп аталады; егер шектеулер жүйесі тек теңдіктерден тұратын болса, онда
сызықтық бағдарламалау есебінің мұндай түрі канондық ( негізгі ) деп аталады.
мақсатты функцияға максималды мән әперетін және теңсіздік пен (2) шартты қанағаттандыратын
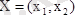 өнімді шығару жоспарын табу керек.
өнімді шығару жоспарын табу керек.
Есептің жалпы түрі
.
 айнымалысы бар
айнымалысы бар
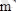 сызықты теңдеулер жүйесі
сызықты теңдеулер жүйесі
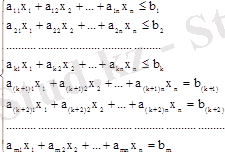 (1)
(1)
және сызықты функция
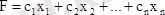 . (2)
. (2)
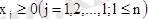 ,
(3)
,
(3)
берілген.
 (2) сызықты функциясына оптималды мән әперетін (яғни максималды немесе минималды) (1) теңсіздік пен (3) шартты қанағаттандыратын
(2) сызықты функциясына оптималды мән әперетін (яғни максималды немесе минималды) (1) теңсіздік пен (3) шартты қанағаттандыратын
 оптималды жоспарын табу керек.
оптималды жоспарын табу керек.
(1) жүйе шектеулер жүйесі, ал функция
 -
сызықты функция, мақсатты функция деп аталады.
-
сызықты функция, мақсатты функция деп аталады.
Сызықты программалау есебінің оптимальды шешімі (немесе оптимальды жоспары) деп
 (2) сызықты функциясына оптималды мән әперетін (яғни максималды немесе минималды) (1) теңсіздік пен (3) шартты қанағаттандыратын
(2) сызықты функциясына оптималды мән әперетін (яғни максималды немесе минималды) (1) теңсіздік пен (3) шартты қанағаттандыратын
 шешімі аталады.
шешімі аталады.
"Шешім" және "жоспар" - синонимдер, бірақ бірінші жиі қолданылады.
(
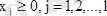 ) теріс емес шарты орындалып, (1) шектеулер жүйесі тек теңсiздiктерден тұрса, онда ондай есеп стандартты деп аталып, ал тек теңдіктер жүйесінен тұратын шектеулер жүйесі канондық, яғни негізгі есеп деп аталады. Жоғарыда келтірілген есеп стандартты есеп.
) теріс емес шарты орындалып, (1) шектеулер жүйесі тек теңсiздiктерден тұрса, онда ондай есеп стандартты деп аталып, ал тек теңдіктер жүйесінен тұратын шектеулер жүйесі канондық, яғни негізгі есеп деп аталады. Жоғарыда келтірілген есеп стандартты есеп.
Сызықты программалаудың кез-келген есебін жалпы, стандартты, канондық түрге келтіруге болады. Келесі мынадай теореманы қарастырайық.
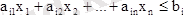 (4)
(4)
теңсіздігінің кез келген
 әрбір шешіміне
әрбір шешіміне
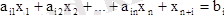 (5)
(5)
мұндағы
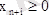 ,
(6)
теңдеуінің анықталған әрбір шешімі сәйкес келеді және керісінше (5) теңдеудің және (6) теңсіздіктің
,
(6)
теңдеуінің анықталған әрбір шешімі сәйкес келеді және керісінше (5) теңдеудің және (6) теңсіздіктің
 шешіміне (4) теңсіздіктің
шешіміне (4) теңсіздіктің
 әрбір шешімі сәйкес келеді.
әрбір шешімі сәйкес келеді.
Осы теореманы пайдаланып, стандартты есепті канондық түрге келтірейік. Ол үшін теңсіздіктер жүйесін теңдіктер жүйесіне ауыстырамыз. Яғни қосымша
 айнымалыларын енгіземіз. Онда теңсіздік белгісі £ болса, айнымалы қосылады, ³ болса, алынады. Сонда жүйе:
айнымалыларын енгіземіз. Онда теңсіздік белгісі £ болса, айнымалы қосылады, ³ болса, алынады. Сонда жүйе:
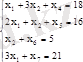 (1. 4)
(1. 4)
Осылайша, (1. 1) стандартты есеп канондық түрде: (1. 4) жүйесін және (1. 2) шартын қанағаттандыратын, (1. 3) функциясын максималды мән әперетін .
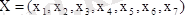 шешімді табу керек.
шешімді табу керек.
1 жағдай.
у=0, 5х+2
у=-1, 5х+6 жауабы (2; 3)
егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер қиылысса, онда теңдеулер жүйесінің бір ғана шешімі болады.
ІІ жағдай.
Теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель
у=-0, 5х+2
у=-0, 5х-3
жауабы: шешімдері болмайды, Ø
егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель болса, онда теңдеулер жүйесінің шешімі болмайды.
ІІІ жағдай.
Жүйедегі теңдеулердің графигі болатын түзулер беттеседі.
7х+2у=12
35х+10у=60
егер теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер беттесетін болса, онда теңдеулер жүйесінің шексіз көп шешімі болады.
І деңгейлік тапсырмалар
№1473 теңдеулер жүйесін графиктік тәсілмен шешу. Оқушылар тақтада орындайды.
у=2х
х-у=3 у=х-3
1. 2 Құрамында параметрі бар квадраттық теңдеулер
ax 2 +bx+c=0 теңдеуі квадраттық теңдеу деп аталады, мұндағы a, b, c тұрақты сандар ал x белгісіз айнымалы.
Жиын уғымы. Жиынның элементтері
Жиын ұғымы математикада негізгі (анықтауға болмайтын, бастапқы) ұғым болып саналады. Сондықтан оны тек мысылдармен ғана түсіндіруге болады. Мысалы, қайсыбір класс оқушыларының жиыны туралы, Әлемдегі планеталар жиыны туралы айтуға болады. «Жиын» сөзі математикада «жиынтық», «класс», «жинақ», «коллекция» деген сөздердің, яғни қайсыбір нәрселер жиынтығын сипаттайтын сөздердің орнына қолданылады, оның үстіне қарастырылып отырған жиынтықты бір ғана нәрсе болуы немесе бірде-бір нәрсе болмауы мүмкін.
Жиын құратын кез-келген нәрселер (адамдар, үйлер, кітаптар, елдер, геометриялық фигуралар, сандар т. б. ) оның элементтері деп аталады. Мысалы, 3 саны - бір таңбалы натурал сандар жиынының элементі. Жиын мен оның элементтерінің арасындағы «элементті болады» деген байланысты «тиісті» сөзінің көмегімен де білдіруге болады. Мысалы, 3 саны бір таңбалы натурал сандар жиынына тиісті деп айтуға болады.
Соңғы сөйлемде символдың көмегімен қысқаша жазуға болады: 3ÏА. Бұл жазуда А әрпі арқылы бір таңбалы натурал сандар жиыны белгіленген (жиынды латын алфавитінің бас әріптерімен белгілейді), ал Îбелгісі «тиісті» сөзін алмастырады.
Жалпы аÎА жазуы «а нәрсесі А жиынының элементті», немесе «а нәрсесі А жиынына тиісті», немесе «А жиынында а элементі бар» деп оқылады. аÏА жазуын «а нәрсесі А жиынына тиісті емес», немесе «А жиынында а элементті жоқ», немесе «а нәрсесі А жиынының элементі емес» деп оқуға болады.
Жиын элементтерінің саны шектеулі де, шектеусіз болуы мүмкін. Мысалы, қайсыбір педучилище оқушыларының жиының элементтерінің саны шектеулі, ал түзудегі нүктелер жиыны шектеусіз.
Жиын ұғымы және онымен байланысты басқа да ұғымдар математиканы алғаш оқытудың негізі болады және онда кеңінен пайдаланылады. Кейбір оқулықтарда «жиын» термині кездеспейді, бірақ бұл ұғым айқындалмаған түрде пайдаланылады, ал бір қатар эксперимент кітаптарда жиын ұғымы символикасымен қоса айқын түрде пайдалалынылады. Сан, натурал сандарды қосу және көбейту амалдары және олардың қасиеттері, геометриялық фигура сияқты маңызды ұғымдардың қалыптасуы мектептегі математика курсында теориялық - жиындық негізде жүзеге асады.
Жиындардың жазылуы мен оның берілу тәсілдері
Егер әрбір нәрсе туралы оның жиынға тиісті немесе тиісті емес екендігін айта алатын болсақ, онда жиын берілген деп саналады.
Жиынды оның барлық элементтерін атау арқылы анықтап беруге болады. Егер де а, b, c, d - әр түрлі нәрселердің белгіленулері болса, онда осы нәрселердің жиынын А={ а, b, c, d } түрінде жазып, оны «А жиыны а, b, c, d элементтерінен тұрады» деп оқиды.
Әрбір нәрсе жиынға тек бір рет қана енеді. Мысалы, 32 545 882 санының әр түрлі цифрларынан тұратын жиын {3, 2, 5, 4, 8}, ал «есеп» деген сөздегі әр түрлі әріптер жиыны {e, c, п} түрінде жазылады.
Жиынның берілуінің тағы бір тәсілі оны құрайтын нәрселердің ортақ қасиетін атау болып табылады. Мұндай қасиетті cипаттамалық қасиет деп атайды. Мысалға, 7-ден кем натурал сандардың А жиынын қарастырайық. Бұл жерде А жиынының барлық элементтерінің ортақ қасиеті, атап айтқанда, олардың «натурал және 7-ден кіші сан болуы» аталып отыр. Қарастырылып отырған А жиынының элементтерін атап шығу қиындыққа түспейді: А={1, 2, 3, 4, 5, 6}
Жиынның осылай берілу тәсілі математикада жиі қолданылады. Мысалға радиусы r, центрі О болатын шеңбердің «центрі О және радиусы r болатын шеңбер деп жазықтықтың О нүктесінен r қашықтықта жататын нүктелер жиынын атайды» деген анықтамасын еске түсірейік. О-дан r қашықтықта және бір жазықтықта жату - центрі О және радиусы r болатын шеңбердің барлық нүктелеріне тән қасиет және бұл қасиетке шеңберге тиісті емес бірде бір нүкте ие бола алмайды.
Элементтердің сипаттамалық қасиеті көрсетілген жиынды былай жазуға болады: фигуралық жақшалар ішіне алдымен элементтерінің белгіленуін жазады. Содан кейін вертикаль сызықша қояды да сызықшадан соң осы жиын элементтеріне және тек соларға ғана тән қасиетті жазады. Мысалы, 7-ден кіші натурал сандар жиыны А былайша жазылады:
А={x/x- натурал сан, x<7}
Сонымен, қандай да бір жиын берілген болуы үшін не оның элементтерін атап шығу, не оның элементтеріне тән қасиетті көрсету керек. Екінші тәсіл біріншіге қарағанда жалпылау екенін айта кетеміз. Мәселе мынада: жиынның элементтерін атап шығу осы жиын шектеулі болғанда ғана мүмкін, ал жиын элементтерінің ортақ қасиетін жиын шектеулі болғанда ғана мү мкін, ал жиын элементтерінің ортақ қасиетін жиын шектеулі болса да, шектеусіз болса да көрсетуге болады.
Бірақ кейбір кезде шектеусіз жиынды да бірінші тәсілді пайдаланып жазып көрсетуге болады. Мысалы, барлық натурал сандар жиынын N әрпі арқылы белгілеп мына түрде
N= {1, 2, 3, 4, …} жазуға болады.
Әрине жиынды тек көп нүктелер орнында не болатыны белгілі жағдайда ғана осы түрде жазуға болады.
Барлық натурал сандардан және нольден тұратын жиынды N 0 арқылы белгілеп, былай жазады:
N 0 ={1, 2, 3, 4, …}
Бұл жиынды оң бүтін сандар жиыны деп атайды.
Барлық бүтін сандар жиынын Z әрпі арқылы белгілеу келісілген: Z={…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5…}
Математиканы оқып-үйрену барысында шешуге тура келетін көптеген есептер элементтерінің ортақ қасиеті көрсетілген жиынды табумен байланысты болады. Бірнеше мысалдар келтірейік.

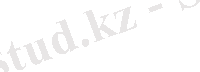 1-мысал.
1-мысал.
х(х-1) =0 теңдеуінің барлық түбірлерінің жиынын табу керек.
Ізделінді А жиынының барлық элементтеріне тән ортақ қасиет -«х(х-1) =0 теңдеуінің түбірі болу», яғни А жиынын А={x x(x-1) =0} түрінде жазуға болады. x(x-1) =0 - теңдеуін шешеміз. Екі х және х-1 сандарының көбейтіндісі, тек сол сандардың біреуі ноль болғанда ғана, нольге тең болатындықтан х 1 =0, х 2 =1 екендігін табамыз. Демек, А={0, 1}.
1 -есеп . Теңдеуді шешіңіз: 3х 2 -х+18=0.
Шешуі . aх 2 - bх + c =0 квадраттық теңдеуінің дискриминанты формуласымен есептеледі. Егер ол оң болса, теңдеудің екі түбірі бар болады да, формуласымен
анықталады; егер де дискриминант нөлге тең болса, онда теңдеудің бір ғана түбірі бар болады да, ол
формуласымен анықталады; ал егер дискриминант теріс болса, онда теңдеудің нақты түбірлері болмайды. Біздің жағдайымызда, сондықтан теңдеудің түбірі жоқ.
Жауабы . Түбірі жоқ.
2 -есеп . Теңдеуді шешіңіз: 3х 2 -14х+16=0.
Шешуі . Дискриминант . Дискриминант оң, сондықтан, және
, .
Жауабы . 2; 2.
3 -есеп . Теңдеуді шешіңіз: 4х 2 -36х+77=0.
Шешуі . Дискриминант. Дискриминант оң, сол себепті
, және, .
Жауабы . 3, 5; 5, 5.
4 -есеп . Теңдеуді шешіңіз: 25х 2 =10х-1.
Шешуі . 25х 2 =10х-1; 25х 2 -10х+1=0. Теңдеудің сол жағы толық квадрат екенін байқасақ: (5х-1) 2 =0; 5х-1=0; х=1:5=0, 2.
Жауабы . 0, 2.
5 -есеп . Теңдеуді шешіңіз: 6х(2х+1) =5х+1.
Шешуі . Алдымен теңдеуді түрлендіріп, квадраттық теңдеуге келтіріп аламыз: 6х(2х+1) =5х+1; 12х 2 +6х=5х+1; 12х 2 +х-1=0. Дискриминант . Дискриминант оң, сондықтан, және, .
Жауабы . -; .
6 -есеп . Теңдеуді шешіңіз: 2х(х - 8) = -х-18.
Шешуі . Алдымен теңдеуді түрлендіріп, квадраттық теңдеуге келтіріп аламыз:
2х(х - 8) = -х-18; 2х 2 -16х=-х-18; 2х 2 -15х+18=0.
Дискриминант . Дискриминант оң, сонда, және теңдеудің түбірлері, .
Жауабы . 1, 5; 6.
7 -есеп . (х+2) (х+4) =0 квадрат теңдеуінің шешімдерін көрсетіңіз.
Шешуі . (х+2) (х+4) =0; көбейтінді нөлге тең болуы үшін көбейткіштердің ең болмағанда біреуі нөлге тең болуы керектігін пайдалана отырып, көбейткіштерді жеке-жеке нөлге теңестіреміз:
1) х+2=0; х=-2;
2) х+4=0; х=-4.
Жауабы . -2; -4.
8 -есеп . х 2 +6х+8 =0 теңдеуінің түбірлерін табыңыз.
Шешуі . Дискриминант. Дискриминант оң, сондықтан теңдеудің екі түбірі бар. , және, .
Жауабы . -4; -2.
9 -есеп . 2х 2 -3х-2=0 теңдеуінің түбірлерін табыңыз.
Шешуі . Дискриминант.
Сонда, , .
Жауабы . -; 2.
10 -есеп . (х+3) (х-4) = -12 теңдеуінің түбірлерін табыңыз.
Шешуі . (х+3) (х-4) =-12; x 2 -4x+3х-12=-12; x 2 -x=0. Толымсыз квадраттық теңдеу алдық, оны көбейткіштерге жіктеу тәсілімен шешеміз: х(х-1) =0; , .
Жауабы . 0; 1.
11 -есеп . Теңдеуді шешіңіз: 3x 2 -2x-5=0.
Шешуі . Дискриминант . , , .
Жауабы . 1; -1.
12 -есеп . Теңдеуді шешіңіз: 2x 2 -5x-7=0.
Шешуі . Дискриминант . , , .
Жауабы . -1; 3, 5.
13 -есеп . Теңдеуді шешіңіз: 6x 2 =5x+1.
Шешуі . 6x 2 -5x-1=0. Дискриминант. , , .
Жауабы . 1; -.
14 -есеп . Теңдеуді шешіңіз: 5x 2 +1=6x.
Шешуі . 5x 2 -6x+1=0. Дискриминант . , , .
Жауабы . 1; .
15 -есеп . Теңдеуді шешіңіз: 4х 2 +7х+3=0.
Шешуі . Дискриминант . Дискриминант оң, сондықтан, , .
Жауабы . -1; -.
16 -есеп . Теңдеуді шешіңіз: х 2 -х-56=0.
Шешуі . Дискриминант. , , .
Жауабы . 8; -7.
ІІ Параметрге тәуелді теңдеулерді шешудің әдіс-тәсілдері
2. 1 Параметр қатысқан сызықтық теңдеулерді аналитикалық және графиктік жолдармен шешу
Сабақтың мақсаты:Параметрлі сызықтық түрдегі теңдеулерді шеше білу.
Сабақ барысы:
1. Үй жұмысын тексеру.
Арнаулы тақта бөлегіне үй жұмысының орындалғанын әркім өзі тексеріп алуы үшін жазып қойылады. (Уақытында көрсетіледі. )
Ауызша есептермен жаттығуды бастаймыз:
1. Логикалық есепті шешіңдер.
Конференцияға қатысқан делегаттардың 85% -і ағылшын тілін, 75 %-і испан тілін біледі. Делегаттардың қандай бөлігі екі тілді біледі?
(85% + 75%=160%, Конференция делегаттарының саны 60%-ке көтерілді.
Неге процент көтеріліп кетті деген сұраққа жауап іздеуден есеп шешімі шығады. Екі тілді де білетіндерді біз екі рет санағанбыз Демек
конференцияға қатысқан делегаттардың
60 % тен кем болмайтыны екі тілді де біледі.
Теңдеудің түбірін табыңдар:
а) 1 + х = 2 - х,
(0, 5)
б) 9х - 4 = 9х + 5,
( ø )
в) 3х + 1 = 3х + 1. (х (R)
b ның қандай мәндерінде теңдеу түбірі санына тең болады?
а) bx = - 6, (b =- 2)
б) 8x = 3b. (b = 8)
Параметрлі теңдеуді шешіңдер:
х = m, ( егер m = 0⋅а) 0
R; егер m∈болса, онда x < 0 болса шешімге ие емес. ) >0 яки m
б)
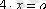 , (х =
а
/4)
, (х =
а
/4)
в)
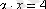 (егер
а
= 0 болса, шешімге ие емес; егер
а
0, онда х =≠
а
/4) .
(егер
а
= 0 болса, шешімге ие емес; егер
а
0, онда х =≠
а
/4) .
Теңдеудің бір шешімін ата
 .
.
Үй жанында қыз бен жігіт отыр. Сәрсен :”Мен -қызбын”-дейді. Ал Гүлнәр : “Мен -жігітпін”-дейді. Егер біреуі жалған айтса, онда қайсы қыз, қайсы жігіт
? (Егер бірі өтірік айтса, онда екіншісі де өтірік айтқан болады. Нәтижеде, Сәрсен -жігіт, ал Гүлнәр -қыз. )
Мысалдар орындау
Бүгін біз параметрлі есептерді аналитик және графиктік әдісте салыстырып орындаймыз.
№1. Теңдеуді шеш:
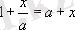
Шешуі:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz