Статистикалық мәліметтерді жинақтау, топтау

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 37 бет
Таңдаулыға:

Дипломдық жұмыс

Статистикалық болжамдарды тексеру

Капарова Айгерм

Мазмұны

Кіріспе

1. Ықтималдықтар теориясы

1.1 Ықтималдықтар теориясы элементтері

1.2 Ықтималдықтар теориясының тарихына шолу

1.3 Ықтималдықтар теориясының өмірде кездесуі

2. Математикалық статистика

2.1 Математикалық статистика элементтері

2.2 Статистикалық мәліметтерді жинақтау, топтау

2.3 Статистикалық болжамдарды тексеру

3. Мектеп курсында ықтималдық-статистикалық білім берудің қажеттілігі

3.1 Қазақстан орта мектептерінде ықтималдықтар теориясын оқытудың
мақсаттары мен оның негізгі ұғымдарын енгізу әдістемесі

3.2 Мектептің математика курсындағы ықтималдық-статистикалық мазмұнның
маңызы

Қорытынды

Пайдаланылған әдебиеттер тізімі

1.1 Ықтималдықтар теориясы элементтері

1.1 Ықтималдық - математикада анықталған шарттарда саны шексіз рет
қайталана алатын қандай да болмасын белгілі бір оқиғаның пайда болуының
мүмкіндік дәрежесінің сандық сипаттамасы оқиғалардың тең мүмкіндігіне (тең
ықтималдығына) сүйенеді. Тең мүмкіндік немесе тең ықтималдық ұғымдары
алғашқы ұғымдарға жатады, олар логикалық (формалды) анықтама беруді қажет
етпейді. Бірнеше оқиғалар тең мүмкіндікті қос-қостан үйлесімсіз және
оқиғалардың толық тобын (жүйесін) құраса, онда ол оқиғаларды сынаудың
мүмкін (мүмкін болатын) нәтижелерінің орнына тең мүмкіндікті барлық
жағдайлар немесе жалпы жағдайлар саны (не жағдайлар) деп атайды. Ал тең
мүмкіндікті үйлесімсіз және оқиғалардың (жағдайлардың) біреуінен бір А
оқиғасының пайда болуы мүмкін, яғни басқаша айтқанда, А оқиғасы тең
мүмкіндікті бірнеше оқиғаларға бөлінеді және олардың кез келген біреуінің
пайда болуынан А оқиғасының пайда болуы шығады. Мысалы, кубты бір рет
лақтырғанда оның кез келген тақ нөмірі А1, А3, А5, пайда болуынан А
оқиғасының пайда болуын байқаймыз. Былайша айтқанда, А оқиғасы тақ нөмірлі
А1, А3, А5 үш оқиғаға (жағдайға) бөлініп отыр. Бұл тақ нөмірлі оқиғалар
саны (ол 3-ке тең) осы А оқиғасына қолайлы жағдайлар болып табылады.
Сонымен, сынау нәтижесінде А оқиғасы бөлінетін мүмкін мәндерді осы оқиғаға
(А-ға) қолайлы жағдай деп атайды. А оқиғасына қолайлы жағдайлар санының (м)
сынаудың тең мүмкіндікті барлық жағдайлар санына (н) қатынасын А оқиғасының
ықтималдығы деп атайды және ол былай жазылады: . Ықтималдықтың бұл
анықтамасын классик. анықтама деп атайды. Оны алғаш рет П.С. Лаплас берген.
Ықтималдықтың бұдан басқа үлкен сандар заңына сүйенген анықтамасы да бар.
Ықтималдық теориясы дегеніміз- жаппай кездейсоқ құбылыстардың
математикалық моделі. Ықтималдық теориясының алғашқы ұғымдарын дүниеге
келтірілген есептер сақтандыру істерін дамытуға байланысты пайда болған.
Лоторея ойындары мен сақтандыру компанияларының өмірге келуі ықтималдық
теориясының дамуына ықпал жасады. Күнделікті тұрмысымызда көптеген
құбылыстар мен олардың өзгерістері кездеседі, солар оқиғаның тууына себепші
болады. Мысалы, металл теңгені жоғары қарай лақтырсақ, ол жоғары көтеріліп
барып, жерге түседі. Осы жасаған әрекетіміз сынақ немесе тәжірибе деп
аталады. Жердегі металл теңгенің елтаңба немесе цифр жағының жоғары
жатуы- оқиға болады. Сақамен тізілген асықтарды атқанымыз- сынақ болады.
Сақаның тізілген асықтарға тиюі немесе мүлт кетуі оқиға болады. Бұл
мысалдан оқиға сынақтың нәтижесі екенін, ал оқиға туғызу үшін сынақ жүргізу
керек екенін аңғарамыз. Оқиғаларды латын алфавиті бас әріптерін пайдаланып
белгілейміз: А,В,С,... .Егер А оқиғасы әр сынақта сөзсіз пайда болса, онда
ол ақиқат оқиға деп аталады. Сынақ кезінде пайда болмайтын оқиға мүмкін
емес деп аталады. Сынақ кезінде пайда болуы да, пайда болмауы да мүмкін
оқиға кездейсоқ оқиға деп аталады.
Адам өмірінің практикалық қажеттілігі ықтималдық негізі бар
жағдайларда шешім қабылдау мен кездейсоқ факторлардың әсер етуіне талдау
жасаумен байланысты. Өмір кездейсоқтыққа толы. Кез келген кездейсоқтыққа
дайын болу үшін кез келген адамда мәліметтерді талдаудың негізгі әдістері,
ықтималдық заңдылықтары және олардың ғылым мен техникадағы, сол сияқты
өнеркәсіп құрудағы рөлі туралы түсінік болуы қажет. Қазіргі нарықтық
экономика жағдайында әрбір адам жас кезінен статистика мәліметтерін
меңгергені дұрыс.
Күнделікті өмірде қандай да бір оқиғаны бағалау нәтижесінде, дәл,
нақты мағынасына мән берместен, ықтималдық ұғымын қолданып жүрміз.
Мысалы, 50 пайыз ықтималдыпен, 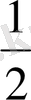ықтималдыпен немесе 100-дің 50
жағдайы, 50-де 50, екіден бір мүмкіндік деген сөз тіркестерін толық
түсініп, жайбарақат қабылдаймыз. Тиынды лақтырмай-ақ, елтаңба жағы мен
цифрдың түссу мүмкіндігі бірдей, ал оқиға нәтижесі 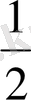санына тең
екеніне келісеміз. Мысалы, егер тиынды лақтыра отырып, әрбір лақтырудан
кейін, айталық 800 рет лақтарылғаннан кейінгі нәтижені тіркеген кезде,
елтаңба жағы 402 рет түскен болса, онда түсудің салыстырмалы жиілігін
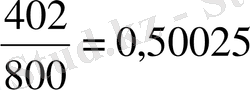аламыз. Әрине, ол дәл 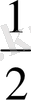емес, бірақ оған өте жақын. Егер әрі қарай
лақтыру (сынақ) санын көбейтсек, онда 402 санына жақынырақ санды алуға
болар еді. Мұндай санның ықтимал болуы мүмкін.
Сонымен, ықтималдық дегеніміз ─ белгілі бір анықталған жағдайда қандай
да бір кездейсоқ оқиғаның пайда болу дәрежесінің сандық сипаттамасы.
Күнделікті өмірде бұл ұғымды жиі қолданамыз. Мысалы, бүгін мүмкін,
кешігермін; ол мүмкін, бос емес шығар; жиналыстың болмауы мүмкін секілді.
Ықтималдық теориясы дегеніміз ─ кездейсоқ жағдайлардың пайда болу
заңдылығын зерттейтін математикалық бөлігі.
Оқиғаның ықтималдығы дегеніміз ─ оқиғаның пайда болу мүмкіндігін
білдіретін сан.
Кездейсоқ оқиғаның бір жолғы тәжірибеде пайда болатынын, не пайда
болмайтынын алдын ала білуге мүкін болмағанымен, қайта-қайта жасалған
тәжірибелер барысында, оның пайда болуының белгілі бір заңдылығы байқалады.
Белгілі жағдайда қайта-қайта n рет тәжірибе жасағанда А оқиғасы m
рет пайда болса, онда 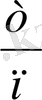қатынасы А оқиғасы пайда болуының салыстырмалы
жиілігі деп аталады. Жоғарыдағы 5 бидай дәнін 5 тәжірибе, яғни m=4 деп
ұғамыз. Сонда оқиғаның пайда болу жиілігі 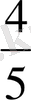немесе 80% болады.
Сол тұрақты 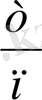саны А оқиғасының ықтималдығы деп аталады да Р(А)
деп белгіленеді.
А және В оқиғаларының қосындысы деп А немесе В оқиғаларының кем
дегенде біреуінің орындалатынын білдіретін оқиғаны айтады және оны А+В
арқылы белгілейді.
Осыдан А+В-ның құрамына А-ға не В-ға тиісті элементтар оқиғалар енеді.
Мысалы, ойын сүйегін тастағанда жұп ұпай түсуі мен үштен кем ұпай
түсуін білдіретін оқиғаларды қосу қажет болсын. Онда 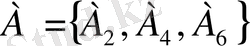және В={А1,А2}
оқиғаларын қосамыз: А+В={ А2, А4, А6}.
А және В оқиғаларының көбейтіндісі деп А және В оқиғаларының қатар
орындалуын білдіретін оқиғаны айтады және оны А*В арқылы белгілейді.
Сонымен, А*В-ның құрамына А-ға және В-ға да тиісті элементар оқиғалар
енеді. Мысал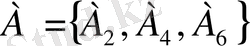ы, және В={А1,А2} оқиғалары үшін А*В={ А2} болады.
А және В оқиғаларының айырмасы деп тек А ғана орындалып, В-ның
орындалмайтынын білдіретін оқиғаны айтады және оны А-В арқылы белгілейді.
Осыдан А-В құрамына тек А-ға ғана енетін және В-ға тиісті емес элементар
оқиғалар енеді. Мысал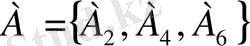ы, және В={А1,А2} оқиғалары үшін А-В={ А2, А4,
А6} теңдіктері орындалады.
Егер А1, А2,...Ап элементар оқиғалары үшін А1+А2+...+Ап=U және Ai*Aj
=Ø (i≠j) шарттары орындалса, онда бұл оқиғаларды элементар оқиғалардың
толық тобы (группасы) деп аталады. Мысалы, ойын сүйегін тастағанда А1,А2,
А3, А4, А5, А6 элементар оқиғалары толық топ құрайды. Шынында да, ойын
сүйегін тастағанда алты ұпайдың бірі түсері ақиқат, яғни А1+А2+ А3+ А4+ А5+
А6=U қосындысы- ақиқат оқиға. Сонымен қатар, бір тастағанда екі түрлі ұпай
түсуі мүмкін емес, яғни Ai*Aj =Ø (i≠j)- жалған оқиға.
Егер В оқиғасы орындалған сайын А оқиғасы да орындалып отырса, онда А-
ны В оқиғасының салдары деп атайды және оны былай белгілейді: ВА.
Мысалы, 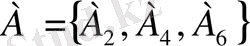және С={ А2, А4} болса, онда А оқиғасы- С-ның салдары. Өзара
кері А және оқиғалары үшін 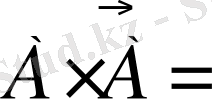Ø және 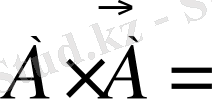U теңдіктері орындалады.
Кездейсоқ оқиғаларды жиындарға қолданылады:

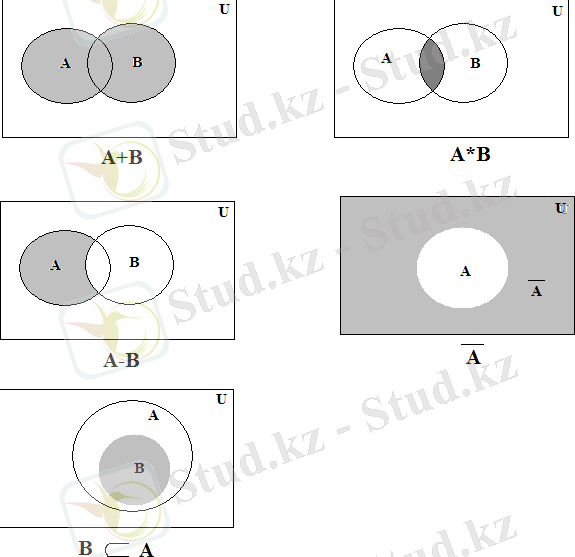
1 ─ Сурет Эйлер-Венн диаграммаларымен бейнелеген қолайлы.

Сонымен бірге, әрбір А және В оқиғалары үшін:
1) ;
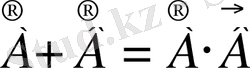2) 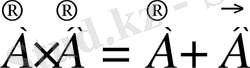теңдіктері орындалады.
Дәлелдеу. 1) Айталық, болсын.
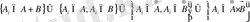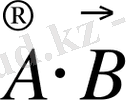Онда. Осыдан және оқиғалары бірдей элементар
оқиғалардан құралғанын көреміз, яғни .
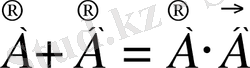2) Осы сияқты дәлелденеді:
1-мысалы: Үш атқыштың біріншісінің нысанаға тигізуін А оқиғасы,
екіншісінің тигізуін В оқиғасы және үшіншісінің тигізуін С оқиғасы деп
алып: 1)А+В; 2)АВС; 3)АВ+АС+ВС өрнектерімен анықталатын оқиғалардың
мағынасын ашып көрсетейік.
Шешуі:1) Нысанаға бірінші немесе екінші атқыш тигізді; 2) Нысанға
бірінші және екінші атқыштар тигізіп, үшінші мүлт кетті; 3) Кем дегенде екі
атқыш нысанаға тигізді.
2-мысал: Алдыңғы мысал шартында нысанаға: 1) тек бірінші атқыш
тигізді; 2) тек екі атқыш қана тигізді; 3) атқыштардың ешқайсысы тигізе
алмады деген оқиғаларды А,В және С арқылы өрнектеу керек.
Шешуі: 1) Нысанаға тек бірінші атқыш тигізіп, қалған екеуі мүлт
кеткен. Онда А, В және С оқиғалары орындалды. Сондықтан оқиғаларды көбейту
ережесі бойынша бұл оқиға 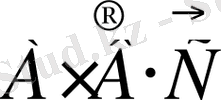арқылы өрнектеледі.
2) Бұл жағдайда нысанға 2 атқыш тигізіп, үшінші міндетті түрде
тигізбеуі қажет, яғни 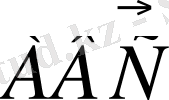немесе 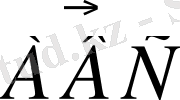немесе 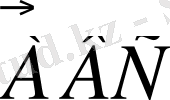оқиғаларының біреуі
орындалуы керек. Сондықтан бізге қажет оқиға 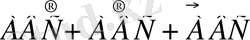қосындысымен
өрнектеледі.
3) Атқыштардың біреуі де нысанаға тигізе алмаса, онда оқиғалары
қатар орындалады, яғни оқиғасы орындалады.
Іс жүзінде адамға заттардың өзара орналасуының барлық мүмкін
жағдайларын есептеуге немесе қандай да бір іс-әрекеттің барлық мүмкін
нәтижелерін және оны орындауға қажетті барлық мүмкін тәсілдер санын
есептеуге тура келеді. Мысалы, әр түрлі 5 кітапты екі оқушыға неше түрлі
тәсілмен үлестіріп беруге болады? Сондықтан мұндай есептерді
комбинаторикалық есептер деп атайды. Ал комбинаторикалық есептерді шешуді
үйрететін математика саласын комбинаторика деп атайды. Комбинаторика
есептерін шешуде қолданатын өзіндік заңдылықтар мен формулалар бар.
Комбинаторикалық формулаларды қолдану кездейсоқ оқиғалардың
ықтималдықтарын есептеуді біршама жеңілдетеді. Мысалдар қарастырайық.
1-мысал: 9 қабатты мекеменің 5-қабатынан лифтке 3 қызметкер мініп,
жоғары көтерілді. Бұлардың әрқайсысы лифттен әртүрлі қабаттарда шығуы
ықтималдылығы қандай?
Шешуі: Мұнда 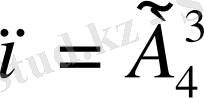-ке тең, себебі жолаушылардың түсуі мүмкін 4
қабатты (4 элементтен тұратын жиынды) үш адамға тағайындап беру қажет (яғни
4-тен 3 бойынша қайталанбалы орналастырулар). Ал 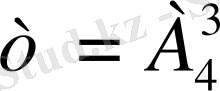-ке тең, себебі 4
элементті (қабатты) 3 орынға (қызметкерлерге) қайталанбайтындай етіп
орналастыру қажет. Сонымен,

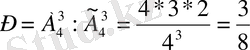
2-мысал: Бес карточкаға бір-бірден а,й,қ,с,ы әріптері жазылып, келесі
бетімен аударылып, мұқият араластырылды. Кездейсоқ бір-бір карточкадан
алып, бір қатарға тізіп шыққанда қайыс сөзінің шығуы ықтималдығы қандай?
Шешуі: Барлық мүмкін нәтижелер саны 5 элементтен тұратын жиынның
алмастырулары санына тең:

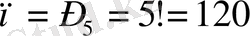
Ал бізге қолайлы нәтижелер саны біреу ғана m=1. Сонда

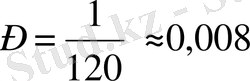
3-мысалы: Сынаптарға ағылшын тілін оқитын бір топта 12 оқушы бар.
Олардың туған күндері әр түрлі айларға түсуі ықтималдығын табу керек.
Шешуі: Барлық мүмкін жағдайлар саны 12-ден 12 бойынша алынған
қайталанбалы орналастырулар санына тең; 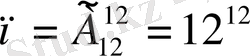. Ал қолайлы жағдайлар саны 12
элементтен алынған барлық орналастырулар санына тең:

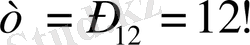
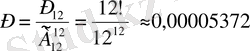
4-мысал: Қорапта қолғаптардың 10 түрлі парлары бар. Қораптан кездейсоқ
4 қолғап алынды. Алынған қолғаптар арасында өзара пар құрайтын қолғаптардың
болмауы ықтималдығы қандай?
Шешуі: 20 қолғаптың ішінен төртеуін түрлі тәсілмен алуға болады,
яғни 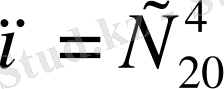. Ал бізге қолайлы жағдайлар саны 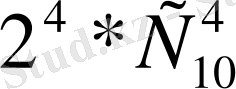-ке тең. Себебі
қолғаптардың 10 парынан 4 сыңарын 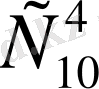түрлі тәсілмен аламыз, ал әр пардан
бір сыңарын 2 түрлі тәсілмен ала аламыз, яғни 4 сыңарды 2*2*2*2=24 түрлі
тәсілмен аламыз. Сонымен

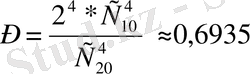
5-мысал: Конверттегі 100 фотосуреттің ішінен бізге қажеттісі біреу
ғана. Конверттен кездейсоқ 10 фотосурет алынды. Алынған суретер ішінде
бізге қажетті суреттің бар болу ықтималдығын анықтайық.
Шешуі: 100 суреттің ішінен 10 суретті 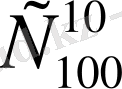түрлі тәсілмен алуға
болады, яғни 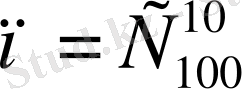. Ал егер алынған 10100 суреттің ішінде бізге қажеттісі
бар болса, онда бұлардың қалған 9-ы бізге қажетсіз. Онда осы қажетсіз 9
суретті 99 қажетсіз суреттер арасынан 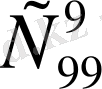. Онда

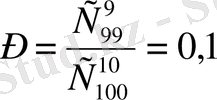
Қорыта айтқанда: Әлемдегі кездейсоқ құбылыстар ерте заманнан бері
зерттеліп келеді. Ол туралы Реньидің де жақсы пікірлері бар. Кездейсоқ
құбылыстарға математикалық тұрғыдан қарау Паскаль мен Фермаға дейін болған.
Демографиялық құбылыстар және адамдарды азық-түлікпен қамтамасыз жиілігінің
біркелкілік фактілері Ежелгі Қытай мен Римде белгілі болған. Кездейсоқ
құбылыстарды нақты әдістердің көмегімен анықтау мүмкіндігін Кордано мен
Галилей де қарастырған.
Паскаль, Ферма және Гюйгенстен басап, кездейсоқ оқиға және оның
ықтималдығы туралы математикалық ғылым- ықтималдық теориясының алғашқы
ұғымдары қалыптаса бастады.
ХХ ғасырдың екінші жартысынан бастап құбылыстардың сандық өлшемдері әр
түрлі процестердің, атап айтсақ, өндірісті математикалық модельдеу мен
ғылыми шығармашылықтың алғашқы шарты болды, яғни ықтималдық ерекше маңызға
ие болды. Оқиға туралы ғылым көптеген мамандық иелерінің: инженерлер,
экономистер, дәрігерлер және әр түрлі шаруашылық саласындағы мамндардың
ортасына енді. Бүкіл әлемде осы ғылымға қызығушылықтың артқаны соншалық,
тіпті ықтималдық теориясы жиі қолданылатын болды деп айтсақ қателеспейміз.
Ықтималдық теориясының негізгі мағынасын ашып ықтималдықтың жиілік
теориясының негізін салған белгілі неміс математигі- Р.Мизес (1883-1953).
Ол ықтималдық теориясын математика пәні емес, математикалық әдістерде
кең қолданылатын ғылым қатарына қосты. Р.Мизес Әр ықтималдыққа берілген
есеп кейбір шынайы процестермен байланысқан,- деп айтқан. Қазіргі
ықтималдық теориясының дамуы, әсіресе А.Н.Колмогоровтың еңбегінде,
ықтималдық теория жоғары математикалық тарауларымен: жиын теориясы, функция
теориясы, функционалдық талдау және т.б. нақты математикалық ықтималдықпен
тығыз байланысқан.
Қазіргі ықтималдық теориясының әдістері қолданылмайтын сала жоқ.
Ықтималдық статистика әдістерін қолдану көптеген ғылым салаларында дәстүрлі
бағыт болуда. Оларға: физика, геодезия, өлшеу теориясы және т.с.с. жаады.
Кейінгі кезде ықтималдық теориясын мединицина және биология, әскери ғылым
мен космонавтика, лингвистика, психология теориясы мен оқыту теориясы, т.б.
ғылымда да қолдана бастады. Одан басқа ықтималдық әдістерінің негізінде
ықтималдық теориясынан шыққан жаңа ғылымдар қатары пайда болуда. Бұлар-
ақпарат теориясы, сенімділік теориясы, сапаны статистикалық бақылау,
тәжірибені жоспарлау.

1.2 Ықтималдықтар теориясының тарихына шолу

Ықтималдықтар теориясы өз бастауын XVII ғасырдан алады.Алдымен азартты
ойындар пайда болды.Араб тілінде азар деген сөз қиын деген мағына
береді.Арабтар азар деп лақтырылған ойын сүйегінің екеуінде де 6 ұпайдан
түсүін айтады екен.Куб түріндегі ойын құралы ол кезде піл сүйегінен
жасалатын болғандықтан ойын сүйегі деген атау сол заманнан қалыптасып
қалған.Ықтималдықтар теориясы жөніндегі алғашқы жұмыстар XVII ғасырда
басталды. Еуропа елдерінде адамды құнықтыратын әр түрлі ойындардың кең
таралуына байланысты әр ойыншы өзінің жеңілмеу ықтималдықдығын алдын ала
анықтауға тырысты.Сол кездегі математиктер де бұл мәселеге назар
аудардып,бірнеше рет қайталанатын кездейсоқ оқиғалар туралы заңдылықтар
ашуға талпынды.Бұл мәселеге алғашқы болып еңбектерін ұсынған:француз
оқымыстысы Блез Паскаль,Пьер Ферма,голландиялық Христиан
Гюйгенс,швецариялық математик Яков Бернулли болды. Француздың атақты
математиктері Пьер Ферма мен Блез Паскальдың азартты ойындар жөніндегі
зерттеулері ықтималдықтар теориясының негізін қалады. Кейіннен сақтандыру
жұмыстарында және демография саласында ықтималдықтар теориясы өз қолданысын
тапты.

Жаратылыстану ғылымдары мен техниканың дамуы ықтималдықтар теориясына жаңа
мәселелер қойды.Ықтималдықтар теориясының дамуын Бернулли, Муавр,
ГауссЛаплас, Пуассон еңбектері көп әсер етті.XIX ғасырдың екінші
жартысыннан бастап бұл саланың дамуына зор әсер еткен В.Я. Буняковский
бастаған математиктер мектебі: П.Л.Чебышев, А.А.Марков, С.Н. Бернштейн,А.Н.
Колмогоров секілді орыс ғалымдары үлкен үлес қосты.
XVIII ғасыр аяғы мен XIX ғасыр басында ағылшын оқымыстысы
А.Муавр,орыс оқымыстыларыЛ.Эйлер,Н.Бернулли,Д.Бе рнулли, француз
П.Лаплас,С.Пуассон,неміс К.Гаусс геодезия мен астраномияның өркендеуіне
қатысты өлшеу қателіктерін бағалау,ату теориясындағы снарядтардың
жағдайларын анықтау үшін ықтималдықтар теориясының рөлін көрсету мақсатында
ғылыми жұмыстар жүргізді.XIX ғасыр ортасында
Ф.Гальтон,Л.Больцман,А.Кетле,А.М.Ля пунов,П.Л.Чебышев, А.К.Калмогоров сияқты
оқымыстылар жиындар теориясы,шақты айнымалылы функциялар
теориясы,функционалдық анализ сияқты жоғары математикалық жаңа табыстарына
сүйенетін ықтималдықтар теориясының өркендеуіне негіз салды.
Ықтималдықтар теориясының дамуына байланысты оның адамзат өмірінде
қолдану мүмкіндігі артты.Жалпы алғанда ықтималдықтар теориясының әдісі
ғылымның барлық саласына өз үлесін қосады.Ал математика ғылымында алатын
орны ерекше.
Оқиғалар ұғымы ықтималдықтар теориясының негізгі ұғымдарының бірі
болып табылады. Белгілі бір шарттар орындалғанда пайда болатын құбылысты
оқиға дейміз.Осы шарттарды іске асыруды сынақ,тәжірибе не бақылау жүргізу
дейміз. Мысалы, лақтырылған асықтың түсуін бақылайық.Ол бүк, шік, алшы,
тәйкі деген жақтарымен түсе алады.Алдын-ала асықтың қай жағы түсетіні
белгісіз болғандықтан оқиға кездейсоқ оқиға деп аталады.Тағы бір мысал ,
біз үлкендіктері бірдей үш параққа А,В,С әріптерін жазып,араластырып, қатар
қойғанда, әр түрлі реттікпен орналаса алады:АВС , АСВ , ВАС , ВСА ,
СВА , САВ. Тәжірибе нәтижесінде пайда болған немесе пайда болмаған
оқиғаны сонымен қатар ол оқиғалардың ықтималдықтар теориясының пәнін
анықтайды.Оқиғаларды латын әріптері А,В,С және т.с.с арқылы
белгілейді.Оқиғалар бірнеше түрге бөлінеді: мүмкін болатын оқиға, мүмкін
емес теңмүмкіндікті,үйлесімсіз, үйлесімді оқиғалар.Сынақ нәтижесінде
міндетті түрде болатын оқиға мүмкін болатын оқиға деп,ал сынақ нәтижесінде
ешқашан орындалмайтын оқиға мүмкін емес оқиға деп аталады.Жәшіктен қосалқы
бөлшектер ішінде стандартқа сай бөлшектер алу тәжірибесі.Осы жәшіктен
стандартқа сай бөлшекті алу міндетті түрде орындалады.Ал ешқашан осы
стандартқа сай емес бөлшекті алу орындалмайды.Яғни стандартқа сай бөлшектер
салынған жәшіктен стандартқа сай бөлшекткер алу оқиғасы мүмкін болатын
оқиға.Ал осы жәшіктен стандартқа сай емес бөлшекті алу оқиғасы мүмкін емес
оқиға болып табылады. Мүмкін болатын оқиғаны U әрпімен белгілейді,ал мүмкін
емес оқиғаны V әрпімен белгілейді.
Бес ақ және бес қара қарындаш бар қораптан ақ қарындаш алу және
қара қарындаш алу оқиғаларының мүмкіндіктері бірдей.Өйткені,ақ қарындаш
саны және қара қарындаш саны бірдей.Ал екі қара және жеті ақ шар алу
оқиғасының теңмүмкіндікті оқиға бола алмайды.Өйткені шарлар саны әр түрлі.
Теңмүмкіндікті оқиға деп-тәжірибедегі оқиғалардың пайда болу
мүмкіндігі бірдей оқиғаларды айтамыз.
Ойын сүйегін бір рет лақтырғанда,тек біреуі ғана
орындалады.Нәтижесінде пайда болатын оқиға қалғандарын болдырмайды.Тағы бір
мысал,оқушы бір емтихан тапсырып,бір мезгілде өте жақсы деген және
жақсы деген баға ала алмайды.Демек,мұндағыөте жақсы және жақсы деген
бағалар алу оқиғалары бір-біріне үйлесімсіз оқиғалар. Кері жағдайда ол екі
оқиға үйлесімді оқиғалар деп аталады.Мысалы,бір оқушы екі емтихан
тапсырып,бірінен өте жақсы деген,ал екіншісінен жақсы деген баға алуы
үйлесімді оқиғалар болып табылады
Үйлесімсіз оқиға дегеніміз-тәжірибедегі оқиғалардың бірінің пайда
болуы басқасын болдырмайтын оқиға..Егер екі үйлесімді оқиғаның біреуі
міндетті түрде жүзеге асса,онда екіншісі біріншісі оқиғаға қарама-қарсы
оқиға деп аталады.
1.3 Ықтималдықтар теориясының өмірде кездесуі.

Адам ойы мен қиялы өте шексіз. Жылдарға, ғасырларға кейіндеп те, ілгерілеп
те алға оза алады. Саналы адам көрсем, білсем, үйренсем деп
тұрады.Көрген,білгенінен ой түйіндейді, қорытынды шығарады. Математика,
физикада қарастырылатын есептер көбінесе бір мәнді анықталады. Мысалы:
қолымызбен тасты лақтырсақ, онда тастың орнын кез-келген уақыт кезеңінде
анықтай аламыз. Бірақ ғылымның әр саласында, техникада, шаруашылық
саласында қолданылатын көптеген есептер бір мәнді анықталмайды.Мысалы:
тиынды лақтырып, оның қай жағымен түсетінін нақты айтуға болмайды. Мұндай
жағдайда осы сияқты есептерді шешуде белгілі бір нақты шешім айтуға
болмайтын тәрізді көрінеді. Алайда бұл тәжірибеде керісінше. Ойын
практикасы көрсеткендей тиынды неғұрлым көбірек лақтырсақ, солғұрлым
әрекеттің жартысында елтаңба жағы түссе, енді жартысында цифр жағы түсетіні
байқалды. Бұл кез- соқ оқиға. Белгілі бір заңдылыққа байланысты. Міне
осындай заңдылықтарды ықтималдық теориясы қарастырады. Ең қарапайым мысал
ретінде тиын лақтыруды алдық. Бірақ ықтималдықтар теориясында бұдан да
күрделірек есептер қарастырылады.Шаруашылықтағы маңызды мәселенің бірі
аудан мен облысты байланыстыратын телефон жүйесін орнату. Бұл да таза
ықтималдық есеп.Мысалы: мұнда орталықтан ауданға телефон жүйесін тарту үшін
қанша сым қажеттігі белгілі болу керек.Өмірде мұндай мәселелер көптеп
кездеседі. Осындай мәселелер өндіріс саласын жоспарлауда,зерттеулер
жүргізуде қолданылады.Мысалы:сынып арасында өткізілетін жарыстардың
нәтижесі дәлірек болу үшін нәтижелер ондық үлеспен, жүздік үлеспен
есептелінеді.Сонда әр сыныптың нәтижесі дәлірек болу үшін қанша таңбаға
дейін алу керек деген сұрақ туындайды.

Неғұрлым сынақ көп жасалынса, солғұрым нәтиже дәл болатыны белгілі.Ал ол
үлкен шығынға әкеледі.Міне, осы арада ықтималдықтар теориясы көмекке
келеді. Адамның күнделікті өмірі,дүниені танып-білу барысы кездейсоқ
оқиғаға толы. Бұл кездейсоқтықтар өмірдің даму заңдылығына кедергі
келтірмейді, керісінше, кездейсоқтық пен заңдылық біріне-бірі әсер
етіп,өмірдің дамуына себепші болады. Кездейсоқтық? Оны оқып үйрену не үшін
қажет?-деп сұрайтын боларсыздар? Шын мәнінде,адамдар,ерте кездің өзінде-ақ
оқиға өмірдегі бір ерекшелік емес,қағида екендігін байқаған. Міне сондықтан
да кездейсоқ құбылыстар туралы ғылым пайда болды. Кездейсоқтық заңдарын
білу қажет.Осыған байланысты мынадай мысал қарастырайық.Барлық ірі елді
мекендерде медициналық жедел жәрдем станциялары бар.Кенеттен және қатты
ауырып қалған адамдарға жедел жәрдем көрсету қажет болатын уақытты алдын
ала болжап айту мүмкін емес.Берілген уақыт аралығында мұндай ауруларға
шақырулардың көптігі қандай болады? Дәрігер мен жедел жәрдем машинасына
аурудың қасында қанша уақыт кідіруіне тура келеді? Бір жағынан,аурулар
жәрдемді өте ұзақ күтпеуі, екінші жағынан дәрігерлер құрамын өте тиімсіз
пайдалану байқалмас үшін,кезекшілік кезінде қанша дәрігер және машина болуы
қажет? Біз шақырту уақыттары,дәрігердің аурудың қасында болу ұзақтығы,
машинаның Жедел жәрдемпунктінен, ауру тұратын үйге дейін жолда болу
ұзақтығы ... кездейсоқ болып табылатын әдеттегі жағдаймен кездесіп
отырмыз.Демек,амал біреу ғана:бұл жәрдем шынында да шұғыл болу үшін, барлық
кездейсоқтықты ескере білу керек. Міне, тіпті осындай күнделікті мәселе де
кездейсоқтықты білуді талап етеді. Сондықтан да оны оқып үйрену
қажет.Осындай практикалық жұмыстарда есептеу әдістерін қолдана білуге
үйрену, жалпы математикалық білім деңгейімді жетілдіру,пән бойынша жүйелі
білімімді қалыптастыру,өмірде кездесетін оқиғаларды сараптай білу менің
міндетім болып отыр.

Математика-нақты ғылым,бір қарағанда кездейсоқтыққа ешқандай қатысы жоқ.
Бірақ, осы кездейсоқтықтың сандық сипаттамасын, ықтималдық ұғымын берген
басқа емес,осы математика. Ықтималдықтар теориясы өмірдегі
кездейсоқтықтарды зерттеп, олардың заңдылықтарын ашады.
2.1 Математикалық статистика элементтері
Математикалық статистика — математиканың бір саласы, бақылау
немесе өлшеу арқылы анықталып, сандар түрінде тізілген деректерді жүйеге
келтіру, өңдеу және солар бойынша тиісті ғылыми және практикалық
қорытындылар шығару жайындағы ғылым.
Байқалған құбылыстар, өлшеу жұмыстары немесе арнайы жүргізілген
тәжірибелердің нәтижелері ретінде табылған сандар жиындарының белгілі бір
шарттарды қанағаттандыратын элементтерінің сандары статистикалық деректер
деп аталады.
Математикалық статистика деректер жиынындағы әрбір элементтің жеке
қасиеттерін сипаттамайды, олар бір топқа жататын бірнеше элементті бірге
қамтиды. Әдетте статистикалық деректер жолдар мен бағаналарға бөлініп,
реттеліп жазылады, олардың негізінде жүргізілетін ғылыми-зерттеу әдісі
статистикалық әдіс деп аталады. Ол ғылым салаларының барлығында
қолданылады, бірақ табиғаты әр түрлі нысандардың статистик. мәліметтерін
бірге қарастыруға болмайды. Соның нәтижесінде әлеуметтік-экономикалық
статистика, статистикалық физика, жұлдыздар астрономиясы, т.б. дербес ғылым
салалары қалыптасқан. Математикалық статистиканың әдістері аса маңызды
параметрлері белгісіз немесе оларды жеткілікті дәлдікпен бақылауға
болмайтын көптеген есептерде шешім табудың тиімді жолдарын табуға мүмкіндік
береді. Математикалық статистикада матем. заңдардың бәрі де қолданылады.
Статистикалық деректерге негіз болатын бақылаулар мен өлшеулерде
кездейсоқ қателер болмай қоймайды. Бұл қателер ықтималдықтар теориясы
бойынша айқындалады. Кейде қолда бар деректер бойынша зерттелетін
заңдылықтың жорымал матем. моделі жасалады. Әрине жорымал болғандықтан, ол
модель шын заңдылықтан алшақтау болады. Алшақтық, яғни модельдің шындықтан
ауытқуы ықтималдықтар теориясы арқылы зерттеліп, анықталады. Белгілі бір
деректің модельде қайталану жиілігі жуық түрде ықтималдық есебіне,
қайталанудың орташа шамасы матем. үміт есебіне келтіріледі. Математикалық
үміттің бағаламасы — бір белгінің үйлестіру сипаттамасы ретінде орта шама,
дисперсияның бағаламасы ретінде қосындысы алынады. Математикалық статистика
көптеген дербес тарауларға бөлініп, онда сан алуан әдістер қолданылады:
таңдап алу, параметрлерді бағалау, статистик. болжамды тексеру, жүйелі
талдау, өнімнің сапасын тексеру әдістері, т.б. Математикалық статистика
қазіргі уақытта экономика және социологиялық зерттеу, социологиялық
зерттеулерде, ш-нда, биология, медицина, физика, геология, психология
ғылымдарында, ауа райын бақылауда және т.б. салаларда зерттеу жүргізу үшін
қолданылады. Математикалық статистиканың алғашқы ұғымдары ықтималдықтар
теориясының негізін салған математиктер (Я.Бернулли, П.Лаплас, С.Пуассон)
шығармаларында кездеседі. Математикалық статистикамен алғаш шұғылданған
Ресей ғалымы Б.Я. Буняковский Математикалық статистиканы демография мен
қауіпсіздендіру мәселелеріне қолданды. Математикалық статистиканың
өркендеуіне 19 ғ-дың 2-жартысы мен 20 ғ-дың басында ықтималдықтар
теориясының классик. орыс мектебі үлкен үлес қосты (П.Л. Чебышев, А.А.
Марков, А.М. Ляпунов, С.Н. Бернштейн). Қазақстанда Қ.Бектаев ықтималдықтар
теориясы мен М. с. әдістерін ақпараттық жолмен ұтымды қолдана білді.

2.2 Болжамдарды статистикалық тексеру

1. Статистикалық болжамдар.
Белгісіз үлестірім түрі немесе белгілі үлестірім параметрлер туралы
болжамды статистикалық болжам дейді. Әрбір ғылым прогресі – болжамдарды
ұсынумен және оларды тексерумен байланысты екені мәлім. Статистикалық
болжамдардың алып тұрған орны ерекше. Статистикалық болжам дегенде
кездейсоқ шаманың (белгінің) не үлестірілуі, не үлестіру параметрі туралы
болжамды айтады.
Бізге (әзірше) белгісіз кездейсоқ шаманың үлестіруі немесе үлестіру
параметрі жайлы ұғым нөлдік (немесе негізгі) болжам Но түрінде айтылады. Но
болжамға қарама-қарсы альтернативті болжам Н1 қойылады. Но болжамға қарама-
қарсы альтернативті болжамдар бірнешеу болуы (Н1 , Н2 , ..., Нк ) мүмкін.
Келешекте бір нөлдік Но болжамы мен бір Н1 альтернативті болжамын
қарастырумен қанағаттанамыз.
2. Бірінші және екінші текті қателер.
Статистикалық болжам әр уақытта кездейсоқ таңдама негізінде орындалады.
Мұндай таңдама көлемі шекті болғандықтан бас жиын үлестіруін идеал деп
сипаттай аламайды. Сонымен қатар мұндай таңдаманы ұйымдастырғанда бас жиын
жайында жалған информация беретін сәтсіз тәуекелділік әр уақытта кездесуі
мүмкін, яғни статистикалық болжамды тексергенде жалған шешімге келу әр
уақытта тууы мүмкін. Олай болса, статистикалық болжамды қандай да бір
критерий көмегімен тексергенде мынадай төрт жағдайдың бірі болуы мүмкін:
1. Дұрыс нөлдік Но болжамы қабылданады, ал оған сәйкес альтернативті
Н1 болжамы дұрыс емес деп, қабылданбайды.
2. Жалған нөлдік Но болжамы қабылданбайды, ал оған сәйкес
альтернативті Н1 болжамы дұрыс деп қабылданады.
3. Дұрыс Но болжамы қабылданбайды, ал оған сәйкес альтернативті Н1
болжамы дұрыс болмаса да қабылданады.
4. Жалған нөлдік Но болжамы қабылданады, ал оған сәйкес альтернативті
Н1 болжамы, дұрыс болса да қабылданбайды.
Алынған екі шешімнің дұрыс, соңғы екі шешімнің қате екенін байқау қиын
емес. Сонымен қатар, үшінші шешім, дұрыс Но болжамын дұрыс емес деу,
бірінші текті қателікті береді, ал төртінші шешім, жалған нөлдік Но
болжамын дұрыс деп қабылдау, екінші текті қателікті береді. Бұл
айтылғандар мына кестеден түсінікті.
Но болжамы дұрыс Но болжамы дұрыс емес
Но болжамын қабылдамау бірінші текті қателік дұрыс шешім
Но болжамын қабылдау дұрыс шешім екінші текті қателік

Ал статистикалық критерийлермен болжамды тексергенде жіберілген қатенің
біреуін болдырмау оны қабылдаудан гөрі құнды болуы мүмкін. Бұл жағдайда
мүмкін қатенің қайсысын болдырмауды құнды десек, сонысын бірінші текті қате
деп қабылдаймыз. Бұл айтылғандардан шын болжамды дұрыс емес деп қабылдамау
бірінші текті қате туғызады деп ұйғаруға болады.
Бірінші текті қате – дұрыс болжамды қабылдамаудан құрылады. Бірінші текті
қатенің ықтималдығы – маңыздылық деңгейі деп аталады және α арқылы
белгіленеді.
Екінші текті қате – дұрыс емес болжамды алудан құрылады. Екінші текті
қате β арқылы белгіленеді.
3. Кризистік облысы.
Болжамды тексергенде оқиға болған кездейсоқ шама К – статистикалық
критерий деп аталады. Таңдама арқылы есептелген критерий мәні Кбақылау деп
белгіленеді.
Нөлдік болжамды қабыл алмау критерий мәндер жиынтығын кризистік облысы
деп атайды. Болжамды қабыл алатын критерий мәндер жиынтығын – болжамды
қабыл алу облысы деп атайды.
Статистикалық болжамды тексеру негізгі принципі мынада: егер бақылау
критерий мәні кризистік облысында жатса – онда болжамды қабыл алмайды; егер
бақылау критерий бақылау мәні болжамды алу облысында жатса – болжамды
қабылдап алады.
Сонымен, статистикалық болжамды тексеру негізгі принципі: егер Кбақыл
кризистік облысында жатса, онда Но қабыл алмайды; ал егер Кбақыл болжамды
қабылдау облысында жатса, онда болжамды қабылдап алады. Кризистік облысын
болжамды қабылдау облысынан бөлетін нүктелерді – кризистік (шекара) Ккр
нүктелер деп атайды. К Ккр теңсіздікпен анықталатын кризистік облысты оң
жақты (мұндағы Ккр 0), ал егер К ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.