Туынды мен дифференциал: теориясы, геометриялық мағынасы және есептеу ережелері


МАЗМҰНЫ:
I. Кіріспе . . . 3
II. Негізгі бөлім.
1 Туынды және оны есепеу . . . 5
2 Туынды функцияны зерттеуге қолдану туындының
геометриялық мағнасы . . . 6
3. Күрделі және кері функциялар туындысы . . . 13
3. 1. Функция диффенерциялы және оның геометриялық мағынасы . . . 16
3. 2. Диффенеренциал табу ережелері . . . 18 3. 3 . Жоғарғы ретті туындылар мен дифференциалдар . . . 21
3. 4 Дифференциалдық есепудін негізгі теоремалары . . . 23
III. Қорытынды . . . 28
Кіріспе
Күнделікті тәжірибемізде біз әр түрлі шамалардың арасындағы тәуелсіздіктермен жиі кездесеміз. Бірнеше шамалдардың бір-бірімен байланысты өзгеруі математикада маңызы өте зор айнымалы шамалар арасында байланыс ұғымын яғни функциялық тәуелділік ұғымын туғызады. Функция ұғымын толығырақ түсіну үшін бірнеше мысалдарды қарастыруға болады. 1 мысал: жеңіл машинаның 60 км сағат жылдамдықпен жүірп өткен жолы қозғалу уақытына тәуелді болады. Жеңіл машина қозғалысының уақытын t, жүрген жолын s әріптерімен белгілейік, сонда ол t сағатына s = 60 t км жол жүреді.
2-мысал: Жұмысшының 10 күнде істеген жұмысының көлемі оның іс өнемділігіне тәуелді жұмысшының істеген жұмысының көлемі V, ал іс өнімділігін а әріпімен белгілейік, сонда ол 10 күнде көлемі V=10a жұмыс істейді.
3 -мысал: Дөңгеліктің ауданы оның радиусына тәуелді. Дөңгеліктің радиуысын r, ал ауданын L әріпімен белгілейік, сонда радиусы r-ге тең дөңгелеіктің ауданы L=πr 2 болады.
Қарастырылған мысалдардың әрқайсысында айнымалы шама екеу мұнда 3 мысалдардағы шамалар t, a, r - еркін өзгереді, ал екінші айнымалы S, V, L бірінші тәуелді өзгереді. Осыған орай соңғыны тәуелді айнымалы шама, ал еркін өзгеретінін тәуелсіз айнымалы шама деп атайды. t мен S, а мен V, r мен L айнымалыларның шамалары өзара тең емес, бірақ олардың арасында байланыс барлығын ескере отырып, оларды сәйкес шамалар деп қана айта аламыз және былай жазамыз: t→S, a →V, r→L, мұнадағы “→” сәйкестік белгісі (а сәйкес V-ға деп оқылады) . Енді тәуелсіз және тәуелді айнымалы шамалары арасындағы байланысты қарастырайық.
1 мысалда байланыс 60-ты t-ға, 2 мысалды 10 а-ға және 3 мысалды r- дің квадратын π-ге көбейту арқылы өрнектелген. Тәуелді айнымалының шамасын тәуелсіз айнымалы арқылы өрнектейтін формула, амалдар арқылы беріліп тұр. Жалпы формуланың тәуелсіз айнымалыға қолданылғандығын келісім бойынша f (x) түрінде жазамыз. f (x) өрнегі у -ке тең, яғни у= f (x), оқылуы у тең х-тен f -ке. Бұл х-ке f заңын қолдану арқылы у-ті аламыз деген мағынаны береді.
Тәуелісіз айнымалы х -тің әрбір мәніне тәуелді айнымалы у-тің бір ғана мәні бір ғана мәні белгілі бір ереже арқылы, сйкестендірілсе, осы сәйкестік заңын функция деп атайды.
Тәуелсіз айнымалыны қысқаша аргумент, ал тәуелді айнымалыны функция деп атайды және у=f (x) деп белгілейді. Х айнымалысының қабылдайтын мәндері болатын х жиыны у функциясының өзгеру аймағы деп аталады. Егер де х-тің әрбір мәніне у-тің бір мәні сәйкес келсе, функция- бір мәнді, ал у-тің бірнеше мәні сәйкес келсе, функция - көп мәнді деп аталады. у=f (x) функциясының берілу тәсілдері:
- Функцияның аналитикалық тәсілмен берілу. Бұл кезде функция формула арқылы беріледі.
- Функцияның кестемен берілеуі. Бұл кезде кестенің бірінші жолына аргумент жазылады да, функцияның берілген аргументке сәйкес мәндері кестенің екінші жолына жазылады.
- Функцияның графиктік тәсілмен берілуі. Жоғарыда келтірілген тәсілдері бойынша функцияның тәртібін, яғни өзгеру заңдылығын бірден аңғару қиынға түседі. Осы кезде функцияның суреті беріледі.
- Функцияның айқындалмаған тәсілмен берілуі. Мысалы үшін, х жиынында жататын кез-келген Х0Є Х үшін F (Х0, y) = 0 теңдеуін шешу арқылы Y жиынында жататын ең болмағанда бір у0Є Y нүктесі табылады да, F (Х0, y0) = 0 тепе теңдігі орындалады. Бұл кезде функция айқындалмаған тәсілмен берілген деп аталады.
- Функцияның күрделенген тәсілмен берілуі. Мысалы: өзгеру аймағы Z жиының болатын Z = f (y) функциясы Ү жиынында анықталған болсын, ал ол кезегінде, өзгеру аймағы Ү жиыны болатын у = f (x) функциясы х жиыныда анықталған болсын. Бұл кезде Z функциясын күрделенген тәсілмен берілген функция деп атайды.
Туынды алу ережелері
Егер U (x) және V (х) дифференициалданатын функциялар болса, онда туынды табудың мынадай ережелері орындалады.
- (U ± V) ´ = U ´± V´
- (U · V) ´ = U ´· V + U · V´
- (C · V) ´ = C · U ´
- ≠ 0
1 Туынды және оны есепеу
Туынды әр түрллі физикалық шамалар уақытқа байланысты өзгеретіндей және олардың өзгеру жылдамдығы маңызды рөл атқаратындай физикалық процесстерді зерттегенде қолдынылады.
Математикалық анализдың негізгі түсініктерінің бірі - функциялардың туындысы болып табылады. у=f (x) функциясы белгілі бір х жиынында анықталған болсын. Осы жиыннан бір х
0
нүктесін алып, оған ∆ х есімшесін беретін және алынған жаңа нүкте х
0
+ ∆ х берілген х жиыныда жататын болсын. Бұл кезде у=f (x) функциясы өзінің ∆ у = f (x
0
+∆ х ) - f (x
0
) есімшесін қабылдайды. Берілген у=f (x) функциясының x
0
нүктесіндегі туындысы деп, осы нүктедегі функция есімшесінің, сәйкес аргумент есімшесіне қатынасының, аргумент есімшесі 0-ге ұмтылған кездегі ақырғы шегін айтамыз және у` (x
0
) немесе f ` (x
0
), әйтпесе
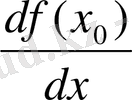 деп белгілейміз. Егер ∆ х = х - х
0
-аргумент есімшесі, ∆ у = f (x
0
+∆ х ) - f (x
0
) - функция есімшесі болса, онда функцияның туындысы f ` (x
0
) =
деп белгілейміз. Егер ∆ х = х - х
0
-аргумент есімшесі, ∆ у = f (x
0
+∆ х ) - f (x
0
) - функция есімшесі болса, онда функцияның туындысы f ` (x
0
) =
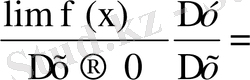
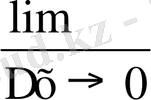
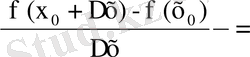
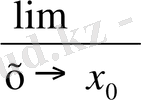
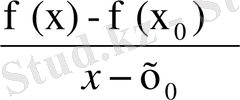 оcы түрде болады.
оcы түрде болады.
Мысал: у=f (x) = х
2
функциясының х
0
= -2 нүктесіндегі туындысын табайық. Туындының анықтамасы бойынша у`
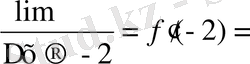
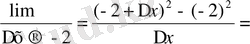
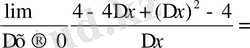
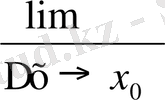 (-4+Δx) = -4;
(-4+Δx) = -4;
2. Туынды функцияны зерттеуге қолдану
Функцияның өсу және кему аралықтары.
Теорема 1: 1) Функцияның өспелі болуының жеткілікті шарты.
Егер (а:в) интервалының әрбір нүктесінде f ` (x) > 0 теңсіздігі орындалса, онда функция осы аралықта өспелі болады.
2) Функцияның кемімелі болуының жеткілікті шарты, егер (а:в) интервалының әрбір нүктесінде f ` (x) < 0 теңсіздігі орындалса, онда функция осы аралықта кемімелі болады.
Туындының геометриялық мағынасы
у=f (x) функциясы х
0
нүктесінің белгілі бір маңайында анқыталған болсын. Осы функция графигінің бойынан алынған А (х
0
, f (x
0
) ) және ß (х
1
, f (x
1
) ) нүктелері арқылы жүргізілген, қиюшысы теңдеуінің канондық теңдеу түрі бойынша
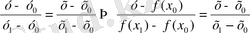 теңдігімен анықталады. Мұндағы х және у қиюшының ағымдық нүктелері. Бұл теңдеулерден
теңдігімен анықталады. Мұндағы х және у қиюшының ағымдық нүктелері. Бұл теңдеулерден
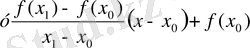 . Осыдан А және В нүктелері арқылы өтетін қиюшы бұрыштық коэффинценті
. Осыдан А және В нүктелері арқылы өтетін қиюшы бұрыштық коэффинценті
R ´ =
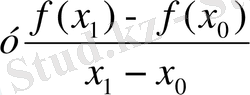 болатынын көреміз.
болатынын көреміз.
Егер В нүктесі үзіліссіз у=f (
x
) функциясы графигі бойымен А нүктесіне қарай жылжитын болса, онда (l) қиюшысы А нүктесінде у=f (
x
) функциясы графигіне жүргізілген (l) жанамаға айналады. Бұл жағдайда 3ші және 2-ші теңсіздіктерден х
1
→х
0
(немесе В→А) кезде,
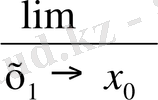
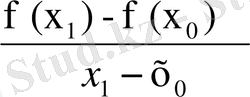 = f ´ (x
0
) теңдігін аламыз.
= f ´ (x
0
) теңдігін аламыз.
Осыдан берілген у=f (x) функциясының х 0 нүктесіндегі туындысы А (х 0 , f (x 0 ) ) нүктесінде берілген функция графигіне жүргізілген жанаманың бұрыштық коэффицениті болатын көреміз, яғни
R = f´ (x
0
) =
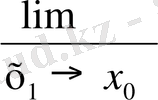
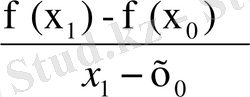 ендеше у =
ендеше у =
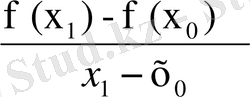 (х-х
0
) + f (х
0
) теңдіктерін пайдаланып у = f´(x
0
) (x-x
0
) + f (x
0
) берілген функция графигіне А нүктесінде жүргізілген (l) жанама теңдеуін аламыз, ал осы жанамаға ортогональ және А нүктесі арқылы өтетін түзулердің ортогональдық шарты бойынша алынған мына теңдеу у = -
(х-х
0
) + f (х
0
) теңдіктерін пайдаланып у = f´(x
0
) (x-x
0
) + f (x
0
) берілген функция графигіне А нүктесінде жүргізілген (l) жанама теңдеуін аламыз, ал осы жанамаға ортогональ және А нүктесі арқылы өтетін түзулердің ортогональдық шарты бойынша алынған мына теңдеу у = -
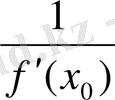 (x-x
0
) + f (x
0
) берілген функция графиігіне А нүктесінде тұрғызылған нормаль түзудің теңдеуі деп аталады. Мысалы: у=f (x) = х
2
- параболаға M
(x-x
0
) + f (x
0
) берілген функция графиігіне А нүктесінде тұрғызылған нормаль түзудің теңдеуі деп аталады. Мысалы: у=f (x) = х
2
- параболаға M
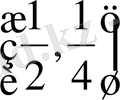 нүктесінде жүргізілген жанама мен нормальдің теңдеуін жазайық. Онда алдымен берілген у=х
2
функция графигінің М нүктесіне жүргізілген жанаманың теңдеуін жазайық. Ол үшін аналитикалық геометриядан белгілі у-у
0
= R (x-x
0
) теңдеуін пайдаланамын. Мұндағы R = f´ (x
0
) =
нүктесінде жүргізілген жанама мен нормальдің теңдеуін жазайық. Онда алдымен берілген у=х
2
функция графигінің М нүктесіне жүргізілген жанаманың теңдеуін жазайық. Ол үшін аналитикалық геометриядан белгілі у-у
0
= R (x-x
0
) теңдеуін пайдаланамын. Мұндағы R = f´ (x
0
) =
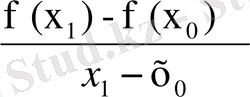 теңдеуі бойынша,
у
=
x
2
функциясының М нүктесіндегі туындысы R = f´ (x
0
) = 2x
теңдеуі бойынша,
у
=
x
2
функциясының М нүктесіндегі туындысы R = f´ (x
0
) = 2x
 R/ x
R/ x
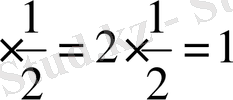
Кей кездерде берілген у = f (х) функциясының х 0 нүктесіндегі туындысы “шексіздікке” тең болады. Бұл кезде мына жағдайлар болуы мүмкін.
а) f´ (x) = + ∞;
ә) f´ (x 0 ) = - ∞;
б) f´ (x 0 - 0) = - ∞ f´ (x 0 +0) = + ∞;
в) f´ (x 0 - 0) = + ∞ f´ (x 0 +0) = - ∞;
Мысалы: у = f (t) - M материалдық нүктенің түзу сызық бойымен қозғалу заңдылығы болсын, яғни f (t) - l өлшем уақыттағы материалдық нүктенің жүріп өткен жолы болсын. Онда М нүктесі t 0 уақытта - f (t 0 ), t 1 - f (t 1 ) жол жүреді.
Ал ∆ t = t
1
- t
0
уақытта ∆ у = f (t
1
) - f (t
0
) жол жүреді. Ендеше, нүкте қозғалысының орташа жылдамдығы функция есімшесі мен аргумент есімшесінің қатынасына тең.
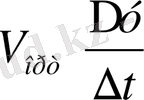 , осы қатынастан аргумент есімшесі ∆ t→0 кездегі шегін қарастырсақ жән ол шек ақырлы болса, V
лж
=
, осы қатынастан аргумент есімшесі ∆ t→0 кездегі шегін қарастырсақ жән ол шек ақырлы болса, V
лж
=

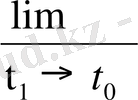
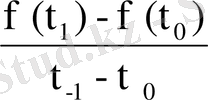 = f `(t
0
) .
= f `(t
0
) .
Материалдық нүкте қозғалысының t
0
уақыт кезіндегі лездік жылдамғын береді. Мысалы: Бос кеңістікте құлаған дененің t уақыттағы лездік жылдамдығын табайық. Шешуі. Еркін түсу қозғаласының заңдылығы S =
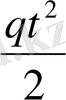 (q - еркін түсу үдеуі) формуласымен өрнектелетіндігі физикадан белгілі. Егер уақытқа есімше берсе, сәйкес функция есімшісі:
(q - еркін түсу үдеуі) формуласымен өрнектелетіндігі физикадан белгілі. Егер уақытқа есімше берсе, сәйкес функция есімшісі:
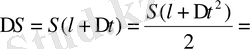
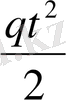 =
=
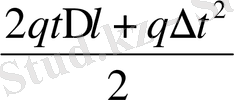 Онда (t, l+∆t) уақыт аралығындағы дененің еркін құлау жылдамдығы
Онда (t, l+∆t) уақыт аралығындағы дененің еркін құлау жылдамдығы
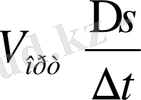

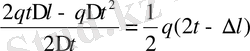
Лездік жылдамдық
V
лж
= S ` (t) =
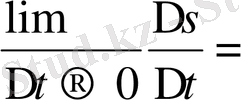
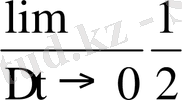
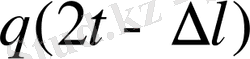 = qt.
= qt.
Дененің еркін түсуінің лездік жылдамдығы уақыт.
Мысалы: Есеп: Айталық материалдық нүкте S= f (t) заңымен қозғалысын. F (t
0
) = S
0
. f (t
1
) = S
1
болса онда
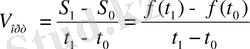 өрнегін t
0
- ден t
1
-ге дейінгі уақыт аралығындағы қозғалыстың орташа жылдамдығы деп атаймыз. . Қозғалыстың әр түрлі кезеңдеріндегі жылдамдықтар әр түрлі болу айқын. Мысалы, автомобильдің жылдамдығы жөнінде сөз қозғайтын болсақ, онда оның белгілі бір уақыт аралығында жүріп өткен жолындағы орташа жылдамдығын аламыз. Бірақ автомобиль жолдың кейбір жерлерінде қозғалысын баяулатуы, ал кейбір жерлерінде үдетуі мүмкін. Сонымен, жалпы алғанда, әртүрлі уақыт аралықтарында автомобильдің орташа жылдымдықтары әр түрлі болады. Дененің еркін түсуі S =
өрнегін t
0
- ден t
1
-ге дейінгі уақыт аралығындағы қозғалыстың орташа жылдамдығы деп атаймыз. . Қозғалыстың әр түрлі кезеңдеріндегі жылдамдықтар әр түрлі болу айқын. Мысалы, автомобильдің жылдамдығы жөнінде сөз қозғайтын болсақ, онда оның белгілі бір уақыт аралығында жүріп өткен жолындағы орташа жылдамдығын аламыз. Бірақ автомобиль жолдың кейбір жерлерінде қозғалысын баяулатуы, ал кейбір жерлерінде үдетуі мүмкін. Сонымен, жалпы алғанда, әртүрлі уақыт аралықтарында автомобильдің орташа жылдымдықтары әр түрлі болады. Дененің еркін түсуі S =
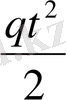 формуласымен анықталады. Техника мен жаратылстанудың көптеген мәселелерін шешуде бізге дененің орташа жылдмадығы емес, оның лездік жылдамдығын білу қажет. Дене S = f (t) заңдылығымен қозғалатын болсын. t = t
0
нүктесінде уақытқа ∆t есімшесін беріп, t
0
мен t
0
+∆t уақыттары аралығында дененің орташа жылдамдығы
формуласымен анықталады. Техника мен жаратылстанудың көптеген мәселелерін шешуде бізге дененің орташа жылдмадығы емес, оның лездік жылдамдығын білу қажет. Дене S = f (t) заңдылығымен қозғалатын болсын. t = t
0
нүктесінде уақытқа ∆t есімшесін беріп, t
0
мен t
0
+∆t уақыттары аралығында дененің орташа жылдамдығы
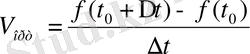
Дененің t =t 0 уақытындағы лездік жылдамдығы U (t 0 ) деп, оның t 0 мен t 0 +∆t аралығындағы орташа жылдамдығының ∆t → 0 шегін айтамыз. Сонымен
F ` (x
0
) =
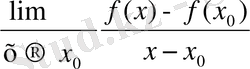 формуласынан х-х
0
= ∆x, (x→x
0
формуласынан х-х
0
= ∆x, (x→x
0
 ∆x→0) белгіленуін енгізсек, анықтаманы былай жазамыз:
∆x→0) белгіленуін енгізсек, анықтаманы былай жазамыз:
y ` =
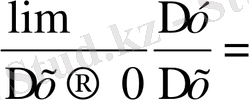
Егер у=f (x) функциясы (а, в) аралығының (мұнда а = ∞, в = + ∞ болуы да мүмкін) . Әрбір нүктесінде туындысы бар болса, онда бұл функцияны (а, в) аралығында диффененциялданады деп айтамыз. Жалпы, фукнцияның берілген нүктедегі туындысын анықтау процессін функцияны дифференциялдау деп атаймыз. Егер Х Є (а, в) болса, онда f ` (x
0
)
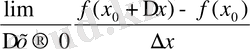 теңдігімен (а, в) аралығында функция анықталатындығы түсінікті. Бұл f `(x
0
) функциясын берілген f (x) функциясының (а, в) аралығындағы туындысы деп атайды.
теңдігімен (а, в) аралығында функция анықталатындығы түсінікті. Бұл f `(x
0
) функциясын берілген f (x) функциясының (а, в) аралығындағы туындысы деп атайды.
Туынды анықтауға мысалдар қарастырайық:
f (x) = C тұрақты функцияның х нүктесіндегі туындысын табуы қажет. Шешуі: алдымен бұл функцияның есімшесін анықтаймыз:
∆ у = f (х+∆ х) - f (х) = С- С =0
сонда С ` туындысы тең
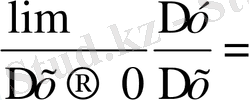
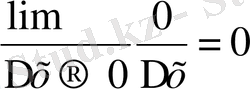 , яғни С`= 0, тұрақты функцияның туындысы 0 -ге тең.
, яғни С`= 0, тұрақты функцияның туындысы 0 -ге тең.
Мысал: f (x) =х функциясының туындысын табайық.
Шешуі: ∆ у = х+∆ х - х = ∆ у = ∆ х -х =∆ у, cонда
x` =
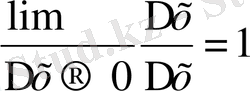
Мысал: f (x) =х 2 - 3 х функциясының туындысын табайық.
Шешуі: ∆ у = (х +∆ х)
2
- 3 (х+ ∆ х ) - (х
2
-3х) = 2х ∆ х- 3∆х + (∆ х)
2
, осыдан (х
2
-3х) ` =
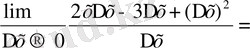
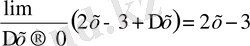
(x 2 -3x) ` = 2x-3
Мысал: f (x) = │х│ функциясының туындысын табу керек.
Шешуі: │х│= x, егер х ≥ 0,
-х, егер, х<0, болғандықтан, х > 0 жағдайында │х│= -х, олай болса (│х│) ` = -1, х<0. Енді бұл функцияның х = 0 нүктесінде туындысы болмайтынын көрсетейік. x = 0 нүктесінде функцияның есімшесі
∆ у = │0+∆ х │- │0 = │∆ х│болады. Онда
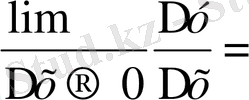
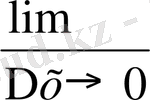
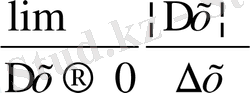 шегі
шегі
анықталмайды. Өйткені
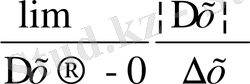 =
=
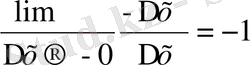
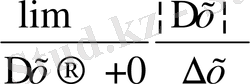 =
=
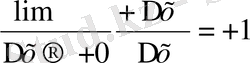 , яғни
, яғни
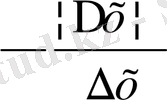 қатынасының сол және оң жақ шектері өз ара тең емес. f ` (x) = (х) ` = 1, егер х > 0,
қатынасының сол және оң жақ шектері өз ара тең емес. f ` (x) = (х) ` = 1, егер х > 0,
-1, егер х < 0,
анықтамаған, егер х = 0
Элементар функциялардың туындылары.
Негізгі элементар функциялардың туындыларының кестесі бар.
Кез келген қарапайым және басқа функциялардан туынды алу үшін оның анықтамасын пайдаланамыз.
y`= f `(x) =
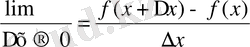
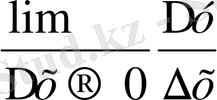
а) у = f (x) = С тұрақты функцияның туындысы
у` = f ` (x) =
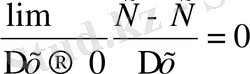 y = f (x) = C;
y = f (x) = C;
- у` = f ` (x) = 0
Сонда С- const туындысы 0-ге тең.
ә) у = f (x) = а
х
, а>х, а ≠1 - көрсеткіштік функциясының туындысы у` = f ` x =
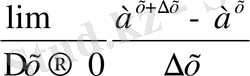 =
=
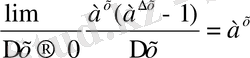
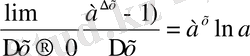
y = f (x) = a x , a >0, a≠1, - y`= f ` (x) = a x lna
y = e
x
 y`= e
x
y`= e
x
б) y = f (x) = x α , α≠-1, a Є R дәрежелік функция
y ` = f `(x) =
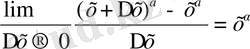 ;
;
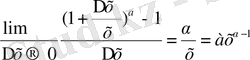
y = f (x) = x
α
 y` = f ` (x) = αx
α-1
y` = f ` (x) = αx
α-1
в) y =f (x) = log a x, a>0, a≠1, x > 0 - логарифмдік функция
y ` = f `(x) =
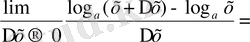
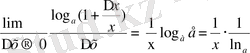 ;
;
y =f (x) = log
a
х
 y ` = f `(x) =
y ` = f `(x) =
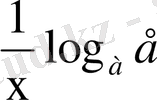 =
=
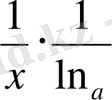
y =f (x) = lnx:
 y ` = f `(x) =
y ` = f `(x) =
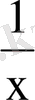
г) а) y = Sinx, y = Cosx. y = tg x; y = Ctg x - тригонометриялық функциялар.
1
0
y ` = f `(x) = (Sinx) ` =
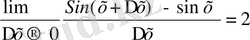
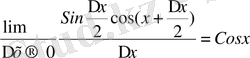
y = Sinx;
 y ` = Cosx
y ` = Cosx
2
0
y ` = f `(x) = (Cosx) ` = [Sin
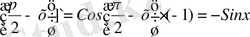
y = Cos x
 y ` = -Sinx
y ` = -Sinx
3
0
y` = f `(x) =
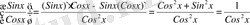
y = tg x
 y` =
y` =
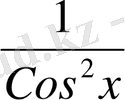
4
0
y` = f `(x) =

y = ctgx;
 -
-
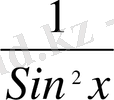
г) y = Shx =
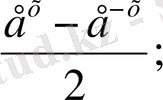 y = Chx =
y = Chx =
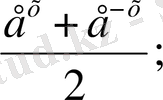
y = thx =
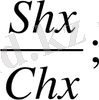 y = Cthx =
y = Cthx =
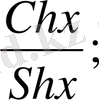 - гиперболалық функция
- гиперболалық функция
а) y` = f `(x) = (Shx) `=
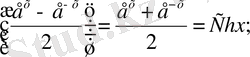
y = Shx
 y`= Chx
y`= Chx
ә) y = Shx
 y`= Shx,
y`= Shx,
б) y = ihx
 y`=
y`=
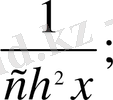
в) y = Сthx
 y`= -
y`= -
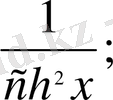
д) y =f (x) = arcsin x, y =f (x) = arccosx,
y =f (x) = arctgx, y =f (x) = arcctgx- тригонометриялық функциялар
y` =f` (x) = (arcsin x) ` =
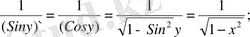
ә) y` =f` (x) = (arcоsx) ` =
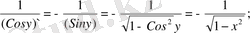
б) y` =f` (x) = (arctg x) ` =
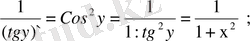
в) y` =f` (x) = (arcсtg x) ` = -
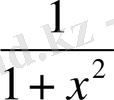
Осы көрсетілген элементар функциялардың туындылар кестесі.
3. Күрделі және кері функциялар туындысы.
- Күрделі функцияның туындысы. Күрделі функциядан туынды алу ережелерін қарастырайық.
Егер y = q (x) функциясы х 0 нүктесінде, ал f (y) функциясы у 0 = q (x 0 ) нүктесінде дифференциялданатын болса, онда f `(x) = f (q(x) ) күрделі функциясы х 0 нүктесінде дифференциялданады және f `(x 0 ) = f `(q (x 0 ) ) · q` (x 0 ) ) теңдігі орындалады.
q (x) функциясы х 0 нүктесінде дифференциялданатын болғандықтан.
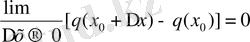 теңдігі орындалады, яғни
теңдігі орындалады, яғни
 Δх→0 ұмтылғанда ∆q→0.
Δх→0 ұмтылғанда ∆q→0.
Сондықтан f (x
0
) =
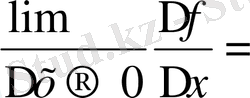
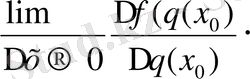
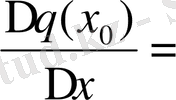
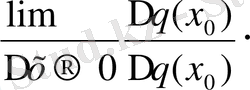
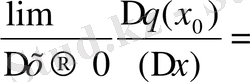 f `(q (x
0
) ) · q` (x
0
) )
f `(q (x
0
) ) · q` (x
0
) )
Мысалы: y = (x 2 -2х+5) 2 функциясының туындысын табайық.
Шешеуі: Егер y = u 2 , y = (x 2 -2х+5) деп аласақ онда бұл функцияны күрделі функция ретінде қарастыруға болады. Сонда х 0 - дің орнынан кез келген х нүктесін алсақ f `(x) = f `(q (x) ) · q` (x) ) формуласы орындалады. Осы формула бойынша y` = (u 2 ) `· (x 2 -2х+5) 2 ` = 24· (2х-2) = 4 (x-1) ·(x 2 -2х+5)
Мысалы: y =f (x) = arctgx (Sin √x) функциясының туындысын табу қажет. Шешуі:
y` =
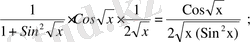
Күрделі функцияның туындысы
y=f (u) функциясы берілсін. Айнымалы u Є U жиынында, ал функция мәндерінің жиыны Ү болсын. Айнымалы u өз кезегінде айнымалы х -ке тәуелді функция болса, яғни и=φ (х), x Є X , онда у = f [φ (x) ] x -аргументі бойынша X жиыны да анықталған күрделі функция болады.
Енді осындай функциялардың туындылары қалай анықталады, осы мәселеге тоқталамыз.
Егер у = f(u) функциясының и нүктесінде, ал и = φ (х) функциясының х нүктесінде туындылары бар болса, онда күрделі функцияның соңғы аргумент х бойынша туындысы бар болады, ол туынды мына
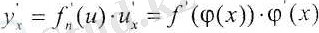
формуламен анықталады.
1-есеп. Күрделі функцияның туындысын табыңыз:
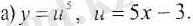
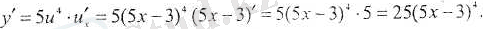
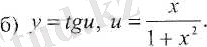
Шешуі
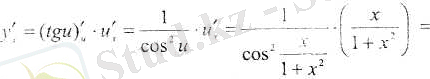
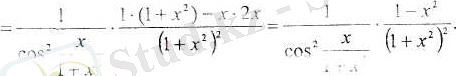
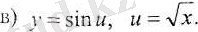
Шешуі:
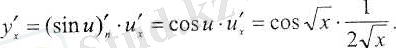
Егер жоғарыдағы кестеде негізгі элементарлық функциялар күрделі функция түрінде берілсе, онда ол функциялардың туындыларын табу үшін сөйкес туындыға аргументтің; туындысын көбейтсе болғаны.
Айталық, y = sinx функциясын аргумент х бойынша күрделі функция деп есептесек, онда осы функцияның туындысы у'=cosx-x' формуласымен анықталады.
Сонда күрделі функциялардың кестелік туындыларының формулаларын жазу үшін, мына кестенің оң жағындағы өрнектерді аргумент туындысына көбейтсе болтаны.
Мысалдар келтірейік. 1 0 . y-tgu, u = x 2 болсын.
Туындысын табайық
Шешуі
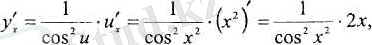
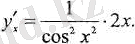
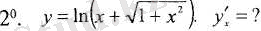
Шешуі:
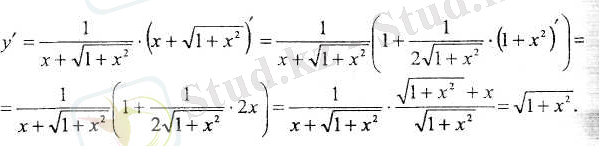
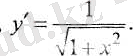
Күрделі функциялардың туындыларының кестесі
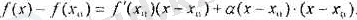
3. 1 Функция диффенерциялы және оның геометриялық мағынасы
Айталық, y=f (х) функциясы х 0 нүктесін дифференциялданатын болсын. Ал, ∆у = y=f (х) -f (х 0 ), ∆х= х-х 0 болғандықтан ∆у =А∆х + α(∆х) · ∆х анықтамасы бойынша f (х) -f (х 0 ) =f` (х 0 ) · (x-x 0 ) + α(х-x 0 ) · (х-x 0 )
Егер f (х 0 ) ≠0 болса, тендіктің екі жағын да f'(x 0 ) (x-x 0 ) шамасына бөліп, ∆х →0 (х→х 0 , α(х-x 0 ) →0 кездегі шекке көшсек,
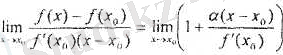
Бұл теңдіктен, х → х 0 кезде f'(x) - f(x 0 ) және f'(x 0 ) (x-x 0 ) функциялары өзара эквивалентті және шексіз аз шама екендігін көреміз. Мұндағы f`(x 0 ) (х-х 0 ) x→x 0 кездегі y = f(x) функциясының бас мүшесі болып табылады және берілген функцияның х 0 нүктесіндегі функция дифференциалы деп аталады да df(x 0 ) түрінде белгіленеді.
Сонымен, анықтама бойынша. функция дифференциалы - df(x 0 ) f`(x 0 ) (х-х 0 ) = f` (x 0 ) ∆x
Erep y = x, dy = ∆ dx = x, яғни дифференциал мен тәуелсіз айнымалы х-тің өсімшесі өзара тең болады. Сондықтан, х 0 нуктесіндегі у = f`(х) функциясының дифференциалын,
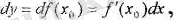 түрінде жазамыз.
түрінде жазамыз.
Алынған теңдіктен х 0 нүктесіндегі берілген у = f`(х) функциясы туындысының тағы да бір жаңа формуласын аламыз
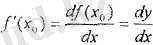
Енді функция дифференциалының геометриялық мағанасын көрсетейік
Айталық: M - у = f(х) функция графигіндегі абцисса х 0 -ге сәйкес нүкте, P - аргументтің х = х 0 + ∆ х мәніне сәйкес нүкте; (l) - функция графигіне M нүктесіне жүргізілген жанама; α - (l) жанама мен Ох өсінің о бағыты арасындағы бұрыш болсын. Онда функция есімшесі NP кесіндісіке тең болады.
Енді ΔMNQ қарастырайық. Бұдан NQ = tga - Δх = f '(х 0 ) Δ) . Демек, функция диференциалы NQ кесіндісіне тең екендігін көреміз.
Сонымен, у = f(х) функциясының х 0 нүктесіне Δх есімше берген кездегі дифференциалының геометриялық мағынасы - функция графигіне М (x 0 , f(x 0 ) ), нүктесіне жүргізілген жанаманың ординатасы болын табылады, ал функция есімшесі, Δy - функция ординатасы,
яғни
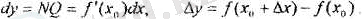
Келтірілген функция дифференциалының геометриялық мағынасы dy<Δy (NQ<NP) екендігін көреміз.
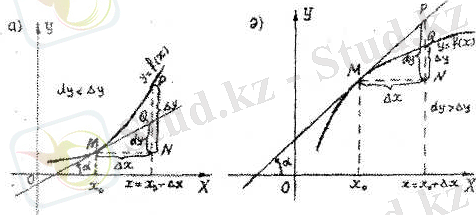
Егер функция графигі дөңес болса, онда функция дифференциалы, функция өсімшесінен үлкен, яғни d y > Δy болады.
Берілген y = f(x) және g(x) функциялары дифференциалдары үшін:
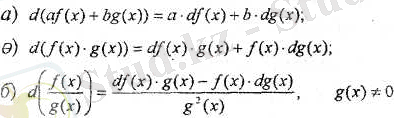
теңдіктері орындалады.
f(x) = 4cosx-2tgx + 3 функциясының х 0 =0 нүктесіндегі дифференциалын табайық.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz