Тізбектер және шегі: анықтамалар, шектеусіз шамалар және Штольц теоремасының қолданылуы


Мазмұны.
І. Кіріспе.
1. 1 Айнымалы шама, варианта (3-4) .
1. 2 Тізбектің анықтамасы, белгілеуі және берілу тәсілдері (4-6) .
ІІ. Негізгі бөлім.
2. 1 Тізбектің шегінің анықтамасы (6-7) .
2. 2 Кейбір маңызды тізбектердің шектері (7-10) .
2. 3 Шектеусіз аз шамалар (10-12) .
2. 4 Шектеусіз үлкен шамалар(12-14) .
2. 5 Шектерді табуды жеңілдететін теоремалар. Теңдікте және
теңсіздікте шекке көшу(14-15) .
2. 6 Шектеусіз аздар туралы леммалар (15-16) .
2. 7 Айнымалыларға қолданылатын арифметикалық
операциялар(16-17) .
2. 8 Анықталмаған өрнектер (17-21) .
2. 9 Штольц теоремасы және оның қолданылуы (21-24) .
ІІІ. Қорытынды.
3. 1 Оқырмандарға ұсынылатын есептер (25) .
Жоспар.
І. Кіріспе.
1. 1 Айнымалы шама, варианта.
1. 2 Тізбектің анықтамасы, белгілеуі және берілу тәсілдері.
ІІ. Негізгі бөлім.
2. 1 Тізбектің шегінің анықтамасы.
2. 2 Кейбір маңызды тізбектердің шектері.
2. 3 Шектеусіз аз шамалар.
2. 4 Шектеусіз үлкен шамалар.
2. 5 Шектерді табуды жеңілдететін теоремалар. Теңдікте және
теңсіздікте шекке көшу.
2. 6 Шектеусіз аздар туралы леммалар.
2. 7 Айнымалыларға қолданылатын арифметикалық операциялар.
2. 8 Анықталмаған өрнектер.
2. 9 Штольц теоремасы және оның қолданылуы.
ІІІ. Қорытынды.
3. 1 Оқырмандарға ұсынылатын есептер.
Айнымалы шама, варианта. Физикада және табиғат жөніндегі басқа ғылымдарда оқырмандарға: уақыт, ұзындық, көлем, салмақ т. т. сияқты көп-теген әр түрлі шамалap кездескен болатын. Бұлардың әрқайсысы жағдайына қарай, кейде түрлі мәндерді қабылдаса, кейде бір ғана мәнді қабылдайды. Сондықтан бірінші жағдайда айнымалы шама туралы, ал екінші жағдайда тұрақты шама туралы сөз болады.
Бірақ математикада қарастырып отырған шаманын, физикалық мағына-сына алаң болмастан, оны өрнектейтін санды ғана қарастырамыз; ал шама-ның физикалық мағынасы математиканың қолданылуымен шұғылданғанда қайтадан өз маңызына ие болады. Сөйтіп, біздер үшін айнымалы шама (не қысқаша - айнымалы) дерексіз не сандық айнымалы болып табылады. Оны қандай да бір символмен (мысалы, х әрпімен) белгілеп оған сан мәнін қоса жазады.
Егер де айнымалы ие бола алатын мәндер жиыны X={х} көрсетілген болса, онда айнымалы берілген делінеді. Х={х} жиыны бір элементтен тұра-ды деп ұйғарғанда, ол тұрақты шаманы көрсететіндіктен, тұрақты шаманы (қысқаша - тұрақтыны) айнымалынынң дербес түрі деп қарастырған қолайлы.
Айнымалы х-тің шегі туралы үғымды тағайындағанда бұл айнымалы мәндері қай сандық жиын Х -тен екендігін ғана білу жеткіліксіз. Айнымалы қандай мәндерді (олардың ішінде қайталайтындары да болуы мүмкін) және қай ретпен қабылдайтындығын білу сөзсіз қажет.
Сандар тізбегі туралы ұғымнан бастайық. Бізге
1, 2, 3, . . . , п, . . . , п', . . . (1)
натурал қатар берілсін дейік, мұндағы сандар өсу ретімен орналасқан, яғни үлкен сан п' кіші сан п -нен кейін келеді (не кіші сан п үлкен сан п' -тің ал-дында тұрады) . Енді, қандай да бір заң бойынша, (1) қатардағы әрбір натурал сан п -ді қандай да бір заттық сан х п - мен алмастырсақ, сонда шығатын мына сандар тізбегінің
х
 ,
х
,
х
 , х
, х
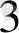 , . . . , х
п
,
. . . ,
х
п
, . . .
(2)
, . . . , х
п
,
. . . ,
х
п
, . . .
(2)
х
п
мүшелері
не
элементтері
барлық натурал сандармен нөмірленіп және ол нөмірлер өсу ретімен орналасады.
п'>п
болғанда,
х
 саны
х
п
-нен үлкен, кіші және тіптен тең екендігіне қарамастан,
х
саны
х
п
-нен үлкен, кіші және тіптен тең екендігіне қарамастан,
х
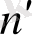 мүшесі
х
п
мүшесінен кейін
(х
п
мү-шесі
х
мүшесі
х
п
мүшесінен кейін
(х
п
мү-шесі
х
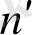 -тің
алдынан) келеді .
-тің
алдынан) келеді .
Қандай да бір мәндер тізбегін (2) қабылдайтын айнымалы х-ті, Мерэ (Сһ. Мегау) атағандай, біз де вaрианта деп атаймыз. [4]
Оқушыға мектептің математика курсынан осы варианта түріндегі айны-малылар кездескен болатын. Мысалы,
a, a + d, a + 2d, . . . , a+(n-1) d, . . .
1 2 3 п
түріндегі тізбек (арифметикалық прогрессия) не
a, aq, aq 2 , . . . , aq n-1 , . . .
1 2 3 n
түріндегі тізбек (геометриялық прогрессия) белгілі. Бұл екі прогрессияның да айнымалы мүшесі варианта болады.
Тағы да
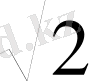 санының біртіндеп артып отыратын ондық жуықтауларын (айталық, кемімен алынған жуықтауларын) еске түсірейік; ол жуықтаулар
санының біртіндеп артып отыратын ондық жуықтауларын (айталық, кемімен алынған жуықтауларын) еске түсірейік; ол жуықтаулар
1, 4; 1, 41; 1, 414; 1, 4142; . . .
1 2 3 4
мәндер тізбегін қабылдайды және де варианта болып табылады.
(2) тізбек мәндерін қабылдайтын айнымалы х -ті көбінесе, бұл тізбектің айнымалы («жалпы») мүшесіне балап, көбінесе х п арқылы белгілейді.
х
вариантасы кейде тікелей
х
п
өрнегі арқылы да беріледі; мысалы, ариф-метикалық немесе геометриялық прогрессияда (ретінше)
х
п
= а+(п-1) d
не
x
n
=aq
 түрінде беріледі. Бұл өрнекті пайдаланып, вариантаның кез келген мәнін, берілген нөмірге қарай, алдындағы мәндерді есептемей-ақ бірден есеп-теуге болады.
түрінде беріледі. Бұл өрнекті пайдаланып, вариантаның кез келген мәнін, берілген нөмірге қарай, алдындағы мәндерді есептемей-ақ бірден есеп-теуге болады.
Басқа жағдайларда (2) тізбектің жалпы мүшесі
х
п
өрнегі белгісіз де болуы мүмкін. Осылай бола тұрса да,
вариантаның белгілі нөміріне қарай оның қалаған мәнін есептеп шығаруға мүмкіндік беретін ережені білсек, онда
(2)
тізбек, онымен бірге оған сәйкес варианта бізге берілген деп есеп-теледі.
Сондықтан да, түбірлерді жуықтап есептеу ережесін білсек,
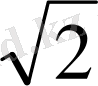 -нің ондық жуықтаулар тізбегінің жалпы мүшесінің өрнегін білмесек те, ол тізбек тұтас берілген деп есептеуге болады.
-нің ондық жуықтаулар тізбегінің жалпы мүшесінің өрнегін білмесек те, ол тізбек тұтас берілген деп есептеуге болады.
Егер де варианта осы мағынада берілген болса, онда мұнымен варианта қабылдайтын барлық мәндер жиыны түгел сипатталып қана қоймай, бұл мәндердің қабылданылу реті де анықталынады; сонымен әрбір нөмірге ва-риантаның тиісті мәні сәйкес келеді және екі мәннің қайсысының нөмірі үл-кен болса, сол мән кейін келеді.
Тізбектің анықтамасы, белгілеуі және берілу тәсілдері.
Тізбек деп барлық оң бүтін сандар жиынында анықталған f функциясын атайды. f функциясыныд п оң бүтін санына сәйкес мәнін х п деп белгілейді, яғни f(n) =x n . [3]
Функция ұғымының ерекше жағдайы - тізбек - математиканың негізгі ұғымдарының бірі. Ол жиі қолданылатын болғандықтан жиі де жазылады. Сондықтан тізбекті белгілеуге ең үнемді символ х п (функцияның аргументі п - ді мәні х п -нің төменгі индексі түрінде жазу) ертеден пайдаланылып келеді. Оның бір себебі х п жазылуы f(n) жазылуына қарағанда екі жақшаға ықшам болуымен қатар, ыңғайлы да.
Тізбектің мәнін, яғни әрбір х п санын, тізбектің мүшесі дейді.
Ілгеріде ыңғайымызға қарай тізбекті мына символдармен белгілейміз:
х
 ,
х
,
х
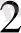 , . . . , х
п
,
. . . ;
, . . . , х
п
,
. . . ;
х
 ,
х
,
х
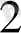 , . . .
;
, . . .
;
{ х
п
}
 Equation. 3
Equation. 3
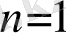 Equation. 3 ; (1)
Equation. 3 ; (1)
{ х
п
}
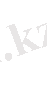 Equation. 3
;
Equation. 3
;
{
х
п
}
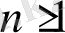 Equation. 3 ;
Equation. 3 ;
п - >х п (n=1, 2, . . . ) ;
п - >х п ;
Егер бұл жаңылушылыққа әкелмесе, онда
«{х
п
}
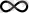
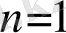 тізбегі» дегеннің орнына қыскаша
«х
п
тізбегі» дейміз.
тізбегі» дегеннің орнына қыскаша
«х
п
тізбегі» дейміз.
Әрине, х -тің орнына басқа да әріптер қолданылады (мысалы, у п , z n , t n , а п , b п , т. б. ) .
Дәл солай, тізбектің аргументін
п
-нен басқа
k, m, i, j, . . .
әріптерімен бел-гілесек те ештеңе өзгермейді. Мысалы,
{ х
п
}
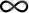
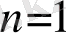 мен
{ х
i
}
мен
{ х
i
}
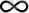
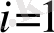 - екеуі де мына бір тізбектің белгілеуі болады:
х
1
х
2
, . . .
- екеуі де мына бір тізбектің белгілеуі болады:
х
1
х
2
, . . .
Тізбекті жалпы карастырғанда немесе тізбектің анықтамасындағы сәй-кестік айқын түрде емес, қанағаттандырылатын қасиеттері арқылы берілсе (мысалы, келешекте анықталатын жинақталу, монотонды т. б. қасиеттер), онда (1) белгілеулері қолданылады. Ал тізбектің анықтамасындағы сәйкес-тікті айқын түрде көрсету қажет болғанда, көбінесе келесі тәсілдерді пайда-ланады:
1°. х п -ді тікелей табу ережесі беріледі; Мысалы, х п =1 (п=1, 2, . . . ) ;
х п =п 2 + 4п + 3 ( n =1, 2, . . . ) ; х п= n (n=1, 2, . . . ) ; т. б.
2°. х п -ді жанама жолмен табу ережесі беріледі; Мысалы,
x l =x 2 =1, х п = х п-1 +х п-2 (n = 3, 4, . . . ), (2)
яғни 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . - бұл Фибоначчи тізбегі.
Белгілі бір k оң бүтін саны үшін тізбектің п-ші (n = k+1, k+2, . . . ) мүшесін тура алдындағы k мүшелері арқылы бейнелейтін формуланы рекуррентті формула дейді (recurrence - латынша «қайтып оралатын» деген) . (2) рекур-рентті формула болады (мұнда k = 2) . Осылай тізбектің рекуррентті формула арқылы анықталуы - жиі қолдаиылатын тәсіл.
3°. Тізбектің мүшелерін табу ережесі сөзбен де берілуі мүмкін; Мысалы, х п -оң бүтін сандар қатарында п-ші болып кездесетін жай сан болсын, яғни 1, 3, 5, 7, 11, . . .
4°. Алғашқы бірнеше мүшесі көрсетілгеннен, «жалпы» мүшесі де танылады; Мысалы, тізбек 1,
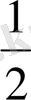 ,
,
 ,
,
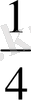 , … түрінде берілсе, онда жалпы мүшесі
х
п
=
, … түрінде берілсе, онда жалпы мүшесі
х
п
=
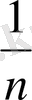 болатыны айқын.
болатыны айқын.
Берілген анықтамада тізбектің мүшелерін 1 санынан бастап оң бүтін сандармен номерледік. Әрине, номерлеуді кез келген бүтін саннан (мысалы, -17, 0, 3- тен) бастасақ та ешнәрсе өзгермейді.
x
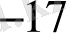 ,
x
,
x
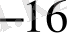 , … x
, … x
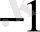 ,
x
,
x
 ,
x
,
x
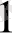 ,
x
,
x
 , …
(3)
, …
(3)
тізбегі
у
п
= x
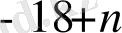 ( n=1, 2, …
) тізбегімен пара-пар, ал (З) -ші тізбектің соңғы түрде жазылуында аргументі 1-ден басталады.
( n=1, 2, …
) тізбегімен пара-пар, ал (З) -ші тізбектің соңғы түрде жазылуында аргументі 1-ден басталады.
Осы тарауда п әрпімен тек қана оң бүтін сандарды белгілейміз. Біз келе-шекте осы ескертулерді арнайы атамай-ақ қолдана береміз.
Тізбектің шегінің анықтамасы. Тізбек және оның шегі ұғымдары математиканың ішкі проблемаларымен қатар оны қолдану жолында пайда болады. Мысалы, біз үшбұрыштың ауданының анықтамасын және оны есептеу жолын біле тұра, радиусы R-ге тең дөңгелектің ауданы деген не және оны қалай табуға болады деген сұрақты қарастырайық.
Әрбір
п
 2
үшін радиусы
R-re
тең дөңгелекке
2
n
бүрышты дүрыс көпбұрыш
S
n
-ді
іштей сызсақ, онда олардың аудандары
х
п
тізбегін құрады. Бір жағынан
п
өскен сайын
S
n
фигурасы дөңгелекке ақырсыз жақындай түседі, екінші жағынан әрбір
п
үшін
S
n
фигурасы деңгелекпен дәл беттеспейді. Сонда деңгелектің ауданы деген не? Дөңгелектің ауданын неге тең деп алу керек?
2
үшін радиусы
R-re
тең дөңгелекке
2
n
бүрышты дүрыс көпбұрыш
S
n
-ді
іштей сызсақ, онда олардың аудандары
х
п
тізбегін құрады. Бір жағынан
п
өскен сайын
S
n
фигурасы дөңгелекке ақырсыз жақындай түседі, екінші жағынан әрбір
п
үшін
S
n
фигурасы деңгелекпен дәл беттеспейді. Сонда деңгелектің ауданы деген не? Дөңгелектің ауданын неге тең деп алу керек?
Осы сұрақтарға жауап беру үшін жаңа түсінік - тізбектің шегі үғымын -енгізу керек. Шек ұғымының негізгі мағынасы мынада: номері өскен сайын тізбектің мүшелері белгілі бір санға акырсыз жақындайды. Сол санды тізбектің шегі деп атайды. Әрине, «номері өскен сайын мүшелері шегіне ақырсыз жақындайды» сөйлемін қандай мағынада түсінетінімізді дәл анық-тауымыз қажет. Бұл келесі анықтамада беріледі.
Егер де мейлінше аз әрбір оң
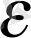 саны үшін N нөмірі табылып, нөмірі n>N болатын барлық х
п
мәндері
саны үшін N нөмірі табылып, нөмірі n>N болатын барлық х
п
мәндері
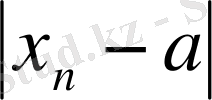 <
<
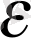 (3)
(3)
теңсіздігін қанағаттандырса, онда тұрақты а санын х = х п вариантаның шегі деп атайды. [4]
а саны варианта шегі екендігін төмендегіше жазады:
limx n =a не lіmx=а
(lіm- «шек» мағынасын білдіретін limes деген латын сөзінің қысқаша түрі) . Екінші сөзбен айнымалыны a-ға ұмтылады деп, оны
х
п
 a не х
a не х
 a
a
түрінде де жазады. Кейде а-ны (2) тізбектің шегі деп атап, бұл тізбекті a-ға жинақталады деп те айтады. Бұл анықтаманы қысқаша былайша да айтады:
Егер х=х п варианта мәндерінің а-дан айырмасы, кейбір орыннан бастап мейлінше аз болса, онда а саны вариантаның шегі болады.
«x
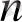 -нің a-дан айырмасы мейлінше аз» дегенді білдіретін осы ұйғарымның дәл жазылу түрі (3) теңсіздік болмақ, онда
-нің a-дан айырмасы мейлінше аз» дегенді білдіретін осы ұйғарымның дәл жазылу түрі (3) теңсіздік болмақ, онда
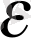 кез келген сан, ал N нөмірі бұл жағдай «қай орыннан бастап» орындалатындығын көрсетеді.
кез келген сан, ал N нөмірі бұл жағдай «қай орыннан бастап» орындалатындығын көрсетеді.
Жалпы айтқанда,
N
нөмірі, әр уақытта бір мәнге ие болмайтындығын ерекше ескеру керек: ол
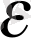 санын қандай етіп алуға байланысты. Осыған ерекше көңіл аудару үшін, біз кейде
N
орнына
N
санын қандай етіп алуға байланысты. Осыған ерекше көңіл аудару үшін, біз кейде
N
орнына
N
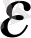 деп жазамыз.
деп жазамыз.
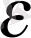 саны кемігенде, оған сәйкес
N=N
саны кемігенде, оған сәйкес
N=N
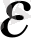 нөмір, жалпы айтқанда, артады: варианта
х
п
мәндерінің a-ға мейлінше жуық болуын талап етсек, (2) қатардан оның тым қашық мәндерін қарастыруға тура келеді.
нөмір, жалпы айтқанда, артады: варианта
х
п
мәндерінің a-ға мейлінше жуық болуын талап етсек, (2) қатардан оның тым қашық мәндерін қарастыруға тура келеді.
Бұл айтылғанға
х
п
вариантаның б а р л ы қ мәндері тұрақты
а
санына тең болған жағдай қосылмайды. Бұл жағдайда а
=lіт х
п
екендігі анық. Бірақ бұл жолы (3) теңсіздік кез ке л г е н
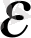 >0 үшін
x
>0 үшін
x
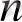 - нің,
барлық мәндерінде орындала береді .
- нің,
барлық мәндерінде орындала береді .
(3) теңсіздіктің мына теңсіздіктермен мәндес екендігі бізге:
-
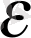 Equation. 3
< х
п
-а <
Equation. 3
< х
п
-а <
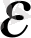 Equation. 3
Equation. 3
не
a -
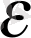 Equation. 3 < x
n
< a +
Equation. 3 < x
n
< a +
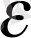 Equation. 3 . (4)
Equation. 3 . (4)
Бұл теңсіздіктерді былайғы жерде жиі пайдаланамыз.
Егер
а, а±
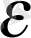 Equation. 3 сандарды және варианта
х
мәндерін сан осіндегі нүктелермен көрсетсек (2-сурет), онда варианта шегінің көрнекі геометриялық түсінігі шығады. Центрі
а
болатын қандай
Equation. 3 сандарды және варианта
х
мәндерін сан осіндегі нүктелермен көрсетсек (2-сурет), онда варианта шегінің көрнекі геометриялық түсінігі шығады. Центрі
а
болатын қандай
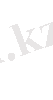
2-сурет.
кішкене кесіндіні (ұзындығы 2
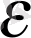 ) алсақ та, кейбір нүктеден бастап б а р л ы қ
х
п
нүктелері осы кесінді ішінде жатуға тиісті (бұл кесіндіден тыс қалатыны тек саны шектеулі нүктелер болуы мүмкін) . Шек a-ны бейнелейтін нүктенің өзі варианта мәндерін кескіңдейтін нүктелердің бір жерге топталып шоғырланғаны сияқты.
) алсақ та, кейбір нүктеден бастап б а р л ы қ
х
п
нүктелері осы кесінді ішінде жатуға тиісті (бұл кесіндіден тыс қалатыны тек саны шектеулі нүктелер болуы мүмкін) . Шек a-ны бейнелейтін нүктенің өзі варианта мәндерін кескіңдейтін нүктелердің бір жерге топталып шоғырланғаны сияқты.
Кейбір маңызды тізбектердің шектері. Енді кейбір жиі кездесетін тіз-бектердің шегін табайық. [3]
Дәлелдеулерін
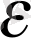 арқылы
К
арқылы
К
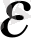 санын табу тәсілдеріне пайдалы жаттығу ретінде қарастыруға болады.
санын табу тәсілдеріне пайдалы жаттығу ретінде қарастыруға болады.
1°.
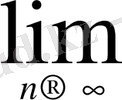
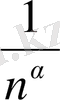 =
=
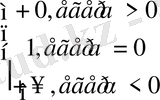
2°.
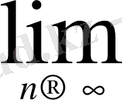 a
a
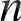 =
=
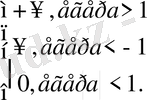 (бірақ +
(бірақ +
 және -
және -
 -ке тең емес)
-ке тең емес)
3°.
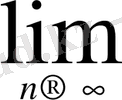 log
log
 Equation. 3 n =
Equation. 3 n =
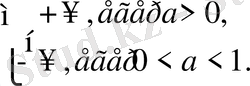 Equation. 3
Equation. 3
4°. Егер
а>1
болса, онда
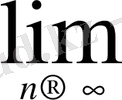
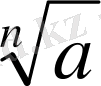 =1+0.
=1+0.
5°.
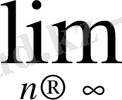
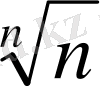 =1+0.
=1+0.
6°. Әрбір
 >0 және
а>1
үшін
>0 және
а>1
үшін
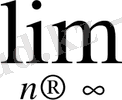
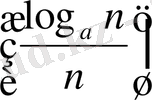
 =0.
=0.
7°.
Әрбір
 >0 және а>1 үшін
>0 және а>1 үшін
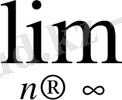
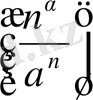 =0, яғни кез келген а>1 үшін
{а
п
}
көрсеткіштік тізбегі кез келген
{п
=0, яғни кез келген а>1 үшін
{а
п
}
көрсеткіштік тізбегі кез келген
{п
 }
дәрежелік тізбегіне қарағанда
}
дәрежелік тізбегіне қарағанда
+
 -ке жылдам ұмтылады, 1°-4°-жағдайларда шектің анықтамасындағы
-ке жылдам ұмтылады, 1°-4°-жағдайларда шектің анықтамасындағы
x
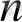
 O
O
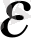 (q)
(q)
кірістіруін анықтайтын теңсіздік
п
арқылы айқын түрде оңай шешіледі, сон-дықтан
K
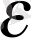 да оңай табылады.
да оңай табылады.
1° - д ә л е л д еу і. а)
 >0 болсын. (8) бұл жағдайда былай жазылады:
>0 болсын. (8) бұл жағдайда былай жазылады:
0
 Equation. 3
Equation. 3
 Equation. 3 <0 +
Equation. 3 <0 +
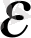 Equation. 3 =
Equation. 3 =
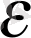 Equation. 3, оның шешімі мынау болады: n>
Equation. 3, оның шешімі мынау болады: n>
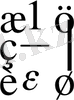
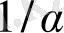 .
.
Сондықтан, K
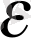 =
=
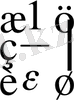
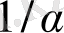 алсақ, мақсатымызға жетеміз:
п
алсақ, мақсатымызға жетеміз:
п
 K
K
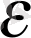
 0
0

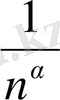 <
<
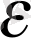 ,
яғни
,
яғни
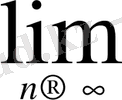
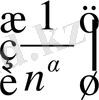 = +0(
= +0(
 >0) .
>0) .
в) а=0 үшін
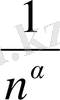 =1 болады, сондықтан
=1 болады, сондықтан
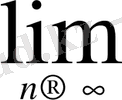
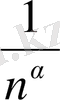 =1
(
=1
(
 =0) теңдігінің орындалуы айқын.
=0) теңдігінің орындалуы айқын.
c)
 <0 болсын. Онда (8) былай жазылады
<0 болсын. Онда (8) былай жазылады
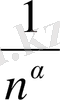 >
>
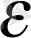 ,
сондықтан K
,
сондықтан K
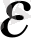 Equation. 3 =
Equation. 3 =
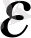 1/
1/
 үшін n> K
үшін n> K
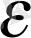 Equation. 3
Equation. 3
 Equation. 3
Equation. 3
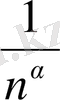 >
>
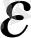 , яғни
, яғни
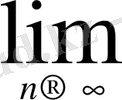
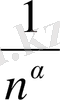 =+
=+
 Equation. 3 (
Equation. 3 (
 Equation. 3 <0) .
Equation. 3 <0) .
2° - д ә л е л д е у і. а) а> 1 болсын. Бұл жағдайда (8) былай жазылады:
а
п
>
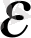 .
(9)
.
(9)
Егер 0<
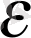
 1 болса, онда (9) барлық
п
үшін орындалады, ал
1 болса, онда (9) барлық
п
үшін орындалады, ал
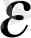 >1 үшін (9) мына теңсіздікке эквивалентті: n
>1 үшін (9) мына теңсіздікке эквивалентті: n
 log
a
log
a
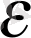 , демек, K
, демек, K
 =mах{1,
log
a
=mах{1,
log
a
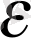 } үшін
} үшін
п>
K
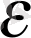
 a
a
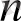 >
>
 , яғни,
, яғни,
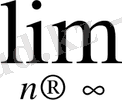 a
a
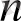 =+
=+
 (a>1) .
(a>1) .
в)
а< -
1 болғанда, (8) мынау болады а
n
=

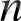 >
>
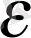 ,
ал a>1 болғандық-тан а) бойынша n>K
,
ал a>1 болғандық-тан а) бойынша n>K
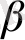 =mах{1, log
=mах{1, log
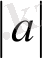
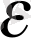 }
}
 a
a
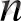 = a
= a
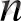 >
>
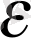 , яғни 1іmа
, яғни 1іmа
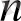 =
=
 (а< - 1) .
(а< - 1) .
с) а<1 үшін (8) былай жазылады
а
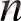 -0 = а
n
<
-0 = а
n
<
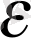 . (10)
. (10)
Әрине,
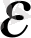
 1 үшін (10) теңсіздігі барлық n-дер үшін орындалады, өйткені а
n
<1. Ал 0<
1 үшін (10) теңсіздігі барлық n-дер үшін орындалады, өйткені а
n
<1. Ал 0<
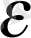 <1 үшін (10) теңсіздігінің шешімі мынау болады: n>log
<1 үшін (10) теңсіздігінің шешімі мынау болады: n>log
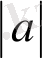 Equation. 3
Equation. 3
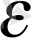 . Сондықтан, n>K
. Сондықтан, n>K
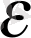 = log
= log
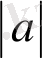 Equation. 3
Equation. 3
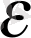


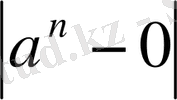 <
<
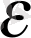 , яғни
, яғни
 a
a
 Equation. 3 = 0.
Equation. 3 = 0.
3° - д ә л е л д е у і. а)
а>
1 болса, онда (8) былай жазыладыг log
 п>
п>
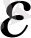 ,
ал оның шешімі мынау болады: n>а
,
ал оның шешімі мынау болады: n>а
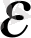 ,
,
 демек, n>K
демек, n>K
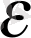 =a
=a
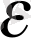
 log
a
n>
log
a
n>
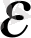 , яғни,
, яғни,
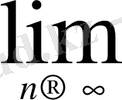 log
log
 n=+
n=+
 (a>1) .
(a>1) .
в) 0<а<1 болсын. (8) бұл жағдайда былай жазылады:
log
a
n<-
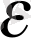 .
(11)
.
(11)
Осы теңсіздікті n арқылы шешейік. 0<а<1 болғандықтан,
a
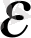 Equation. 3
>a
-log
Equation. 3
>a
-log
 Equation. 3 n
демек, (11) теңсіздіғі
п>
Equation. 3 n
демек, (11) теңсіздіғі
п>
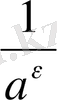 теңсіздігіне эквивалентті.
теңсіздігіне эквивалентті.
Сондықтан n>K
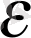 Equation. 3 =
Equation. 3 =
 Equation. 3 log
a
n<-
Equation. 3 log
a
n<-
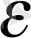 Equation. 3, яғни
Equation. 3, яғни
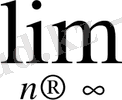 Equation. 3 log
a
n=-
Equation. 3 log
a
n=-
 Equation. 3 (0<а<1) .
Equation. 3 (0<а<1) .
4°-дәлелдеуі.
а>1
болса, (8) былай 1

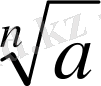 <1+
<1+
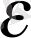 жазылады да
п
арқылы шешімі мынадай болады:
жазылады да
п
арқылы шешімі мынадай болады:
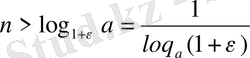
демек,
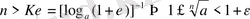
яғни
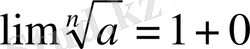
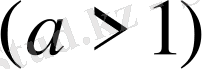
5°-7° мысалдарын дәлелдеу үшін {
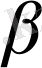
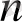 } көмекші тізбегін құрамыз. Ол үшін
} көмекші тізбегін құрамыз. Ол үшін
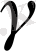
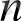 >
>
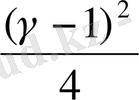
 n
n
 (
(
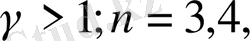 …) (12)
…) (12)
теңсіздігін пайдаланамыз.
5°-д ә л е л д е у і. Біз
п
арқылы 0<
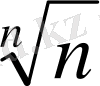 -1 <
-1 <
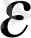 теңсіздігін шешуіміз қажет.
теңсіздігін шешуіміз қажет.
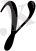 =
=
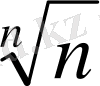 үшін (12) теңсіздігі былай жазылады: n>
үшін (12) теңсіздігі былай жазылады: n>
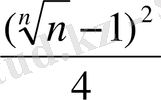
 n
n

 яғни, 0<
яғни, 0<
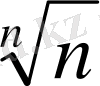 -1<
-1<
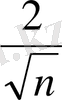 =
=
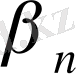 .
.
Әрине,
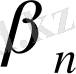 =
=
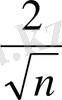 <
<
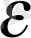 теңсіздігін шешу оңай: n>
теңсіздігін шешу оңай: n>
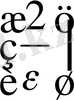
 .
.
Сондықтан,
n>K
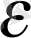 =
=
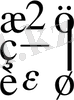
 + 2
+ 2
 1<
1<
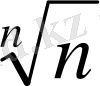 <1+
<1+
 , (13)
, (13)
яғни
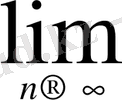
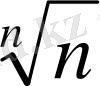 =1 + 0.
=1 + 0.
6°-дәлелдеуі. Бізге
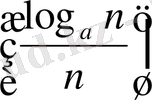
 <
<
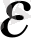 (14)
(14)
теңсіздігін
п
арқылы шешу керек. а>1 болғандықтан, a
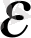
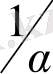 -1 оң сан болады, демек, (1З) -тегі
-1 оң сан болады, демек, (1З) -тегі
 санының орнына осы санды қойсақ, онда (13) былай көшіріледі:
санының орнына осы санды қойсақ, онда (13) былай көшіріледі:
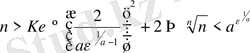
ал соңғы теңсіздік (14) теңсіздігіне пара-пар болғандықтан, 6° дәлелденді.
7°-дәлелдеуі. Біз
п
арқылы мына
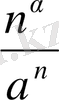 <
<
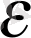 теңсіздікті шешуіміз қажет.
а>1
және а>0 болғандықтан a
1/
теңсіздікті шешуіміз қажет.
а>1
және а>0 болғандықтан a
1/
 >1, демек,
>1, демек,
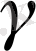 = а
1/
= а
1/
 үшін (12) теңсіздігінен мынау шығады:
үшін (12) теңсіздігінен мынау шығады:
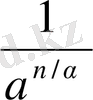 <
<
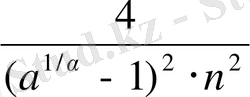 ,
,
сондықтан,
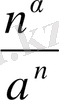 =
=
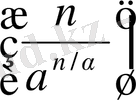
 <
<
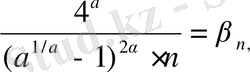
ал
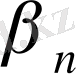 <
<
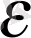 теңсіздігінің шешімі мынадай болады:
теңсіздігінің шешімі мынадай болады:
n>
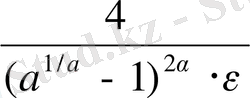 .
.
Осының бәрін қорытындылап, мынаған келеміз
n> K
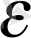 =
=
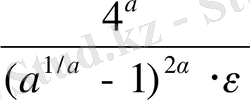

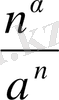 <
<
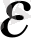 ,
,
яғни, lim
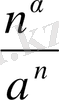 =0 (
=0 (
 , a>1) . 7° дәлелденді.
, a>1) . 7° дәлелденді.
Шектеусіз аз шамалар.
Варианта нольге ұмтылған, яғни х
п
 0, жағдайға ерекше назар аударылады.
0, жағдайға ерекше назар аударылады.
Шегі ноль болатын варианта х п шектеусіз аз шама, немесе шектеусіз аз деп аталады. [4]
Егер варианта шегінің анықтамасында а = 0 десек, онда (3) теңсіздік былай жазылады:
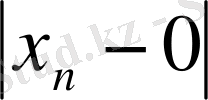 =
=
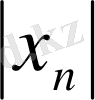 <
<
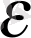 (n>N
(n>N
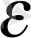 Equation. 3 үшін
) .
Equation. 3 үшін
) .
Сөйтіп, шектеусіз аздың жоғарыдағы анықтамасын «шек» терминін кірістірмей толық түжырымдауға болады:
егер кейбір орыннан бастап варианта х
п
-нің абсолют шамасы алдын ала берілген мейлінше аз
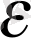 >0
санынан кем болып
және бұдан былай да к е м болып қалып отырса,
онда ол варианта
х
п
шексіз аз делінеді.
>0
санынан кем болып
және бұдан былай да к е м болып қалып отырса,
онда ол варианта
х
п
шексіз аз делінеді.
Қолайсыз (тарихи қалыптасып) алынған «шектеусіз аз» шама терминін оқырман дұрыс түсінетін болу керек: бұл шаманың жеке алынған ешқандай мәні, егер ол ноль болмаса, «аз» деп қарастырылмауға тиіс. Мұның мәнісі, мынау: өзінің өзгеру процесінде тек қалауымызша алынған
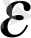 санынан кем болатын айнымалы шама ғана шектеусіз аз болады
.
санынан кем болатын айнымалы шама ғана шектеусіз аз болады
.
Егер де шегі а болатын варианта х п -нің жалпы түріне қайта оралсақ, онда айнымалы мен оның шегінің
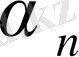 = х
п
- а
= х
п
- а
айырмасының шектеусіз аз болатындығы ақиқат: өйткені (3) бойынша
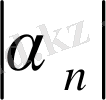 =
=
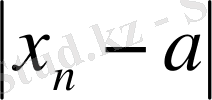 <
<
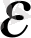 (n>N
(n>N
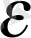 Equation. 3
үшін) .
Equation. 3
үшін) .
Керісінше, егер
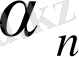 шектеусіз аз болса, онда
х
п
шектеусіз аз болса, онда
х
п
 а.
Бұдан біз мынадай қорытындыға келеміз:
а.
Бұдан біз мынадай қорытындыға келеміз:
варианта х п -нің шегі тұрақты а саны болу үшін, олардың айырмасы
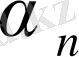 =х
п
- а шектеусіз аз болуы қажетті және жеткілікті.
=х
п
- а шектеусіз аз болуы қажетті және жеткілікті.
Осыған байланысты «шек» ұғымына да басқаша (бұрынғымен пара-пар) анықтама беруге болады:
егер варианта х п мен тұрақты а санының айырмасы шектеусіз аз шама болса, а саны варианта х п -нің шегі делінеді.
Әрине, егер шектің осы анықтамасын қабылдасақ, онда шектеусіз аздың жоғарыдағы екінші анықтамасын пайдалану керек. Бұлай болмаса, шек шектеусіз аз арқылы анықталып, ал шектеусіз аз шек арқылы анықталып шырмаудан шыға алмай қалған болар едік!
Сөйтіп, егер варианта
х
п
 а
болса, онда оны
а
болса, онда оны
х
п
= а +
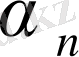
түрінде жазуға болады, мұндағы
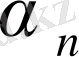 - шектеусіз аз және керісінше, егер варианта x
- шектеусіз аз және керісінше, егер варианта x
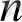 -ді осылай өрнектеу мүмкін болса, онда оның шегі
а
болады. Мұны айнымалы шегін анықтау үшін практикада жиі қолданады.
-ді осылай өрнектеу мүмкін болса, онда оның шегі
а
болады. Мұны айнымалы шегін анықтау үшін практикада жиі қолданады.
Мысалдар:
1) Мына варианталарды қарастырайық:
x
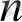 Equation. 3 =
Equation. 3 =
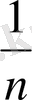 Equation. 3, x
Equation. 3, x
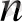 Equation. 3 = -
Equation. 3 = -
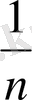 Equation. 3, x
Equation. 3, x
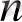 Equation. 3 =
Equation. 3 =
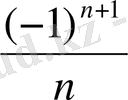 Equation. 3 ;
Equation. 3 ;
оларға төмендегі мәндер тізбектері сәйкес келеді:
1,
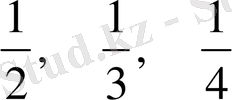 , …,
, …,
-1, -
 , …,
, …,
1, -
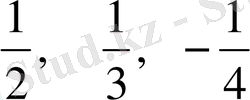 , … .
, … .
Айнымалылардың үшеуі де шектеусіз аздар болады, яғни олардың шегі 0-ге тең. Шынында да, тек n>
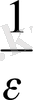 болса, олар үшін
болса, олар үшін
 =
=
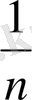 <
<
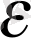
болады. Сөйтіп, N
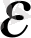 үшін, мысалы,
үшін, мысалы,
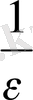 бөлшегіндегі ең үлкен бүтін санды, яғни E(
бөлшегіндегі ең үлкен бүтін санды, яғни E(
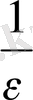 ) санын алуға болады.
) санын алуға болады.
Бірінші айнымалы әр уақытта өзінің шегі нольден артық, екінші айныма-лы әр уақытта одан кем, үшінші айнымалы өз шегі 0-ден кезекпен бірде ар-тық, бірде кем болып отыратындығын ескертеміз.
2) Егер
x
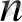 Equation. 3 =
Equation. 3 =
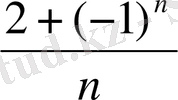 Equation. 3
Equation. 3
десек, онда айнымалы төмендегі мәндер тізбегін қабылдайды:
1,
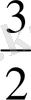 Equation. 3,
Equation. 3,
 Equation. 3,
Equation. 3,
 Equation. 3,
Equation. 3,
 Equation. 3,
Equation. 3,
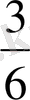 Equation. 3, …
Equation. 3, …
Бұл жағдайда да
х
п
 Equation. 3
0, өйткені
п>
Equation. 3
0, өйткені
п>
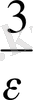 үшін
үшін
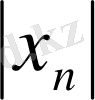 Equation. 3
Equation. 3

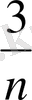 <
<
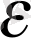 Equation. 3
Equation. 3
олай болса
N
 Equation. 3
үшін E
Equation. 3
үшін E
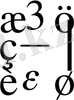 Equation. 3 санын алуға болады.
Equation. 3 санын алуға болады.
Бұл мысалда біз ерекше жағдайға кездесіп отырмыз: айнымалы өзінің шегі 0-ге кезекпен біресе жуықтап , біресе одан алыстайды.
3) Енді
x
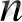 Equation. 3 =
Equation. 3 =
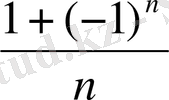 Equation. 3
Equation. 3
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz