Ұқсастық түрлендіру және оның аналитикалық мағынасы: мектеп геометриясында есеп шығарудың әдістемесі


Қостанай мемлекеттік педогогикалық институты
жаратылыстану-математика факультеті
физика-математика кафедрасы
Ануарбекова Айгерим Хамитовна
«Ұқсастық түрлендіру және оның аналитикалық мағынасы»
курстық жұмыс
Қостанай, 2018
Мазмұны
Кіріспе 3
1 Ұқсас түрлендірудің теориялық мәні 5
1. 1 Ұқсастық түрлендірудің негізгі әдістері 5
1. 2 Ұқсас түрлендіру анықтамасы 5
1. 3 Үшбұрыштардың екі қабырғасы және олардың арасындағы бұрышы бойынша ұқсастық белгісі 9
2 Мектеп геометрия курсындағы ұқсас түрлендіру бойынша есеп шығару ерекшеліктері 11
2. 1 Ұқсас түрлендірулердің есептері 11
2. 2 Түрлендіру әдісін қолдану 18
Қорытынды 24
Пайдаланған әдебиеттер тізімі 25
Кіріспе
Тақырыптың өзектілігі. Геометрияны оқытуда есептерді шеше білу дағдысын қалыптастыру және оны жалпы түрде дамыту аса маңызды мәселелердің бірі болып табылады. Геометриялық есептерді шешу туралы жалпы білік - дағдылар әдетте көптеген есептерді шешу арқылы қалыптасады. Олай болса, мұғалім мен оқушының жүйелі түрде ұзақ уақыт еңбектенуіне тура келеді. Шешілу жолы беймәлім, әр түрлі теориялық фактілерді байланыстыруды қажет ететін, оқушылар шығара алмайтын жаңа есептер де жиі кездеседі. Сондықтан оқушыларды кез келген геометриялық есепті шешудің жалпы тәсілдерімен қаруландыру керек.
Есептерді геометриялық әдіспен шешкенде логикалық ойлаудың жәрдемімен белгілі теоремалар арқылы тұжырымдауды қажет ететін сөйлемдерді дәлелдейміз. Ал есептерді алгебралық әдіспен шешкенде ізделген шаманы табу, не тұжырымдауға тиісті сөйлемді дәлелдеу тікелей есептеу жолымен немесе теңдеулер мен олардың жүйелерін құру арқылы іске асады. Тікелей есептеу әдісінің мәні мынада: есептің берілгендері мен белгісіздерінің жан-жақты байланыстарынан аралық қосымша белгісіз шамалар тізбегі құрылады, тізбекке қатысатын әрбір белгісіз шама анықталады немесе іздеген шама белгілі шамалар арқылы өрнектеледі.
Мектеп геометрия курсын оқытудың негізгі мақсаты - оқушылардың геометрия ғылымының негіздерін меңгеруі мен оларды практикаға қолдануға үйрету, кеңістік түсінігін және елестетуін қалыптастыру, логикалық ойлауын дамыту, негізделген, тұжырымды ой қорытуы мен дәлелдеу қабілетін жетілдіру, ойды дәл және анық жеткізе алу. Осы мақсаттарға жету есептер шығару іс - әрекетін меңгерумен бірге жүзеге асады. Есептер шығару нәтижесінде оқушылар алған білімдерін тиянақтап, теориялық материалды қолдана білуге үйренеді, есеп шығара отырып жаңа білімдер алады. Сонымен қатар, есептер шығару - оқушылардың талдау, жинақтау, салыстыру, жалпылау, нақтылау т. б. ойлау операциясын меңгеретін де ортасы.
Жоғарыда айтылғандар осы зерттеу жұмысы үшін тақырыпты таңдаудың өзектілігін көрсетеді.
Зерттеу нысаны - мектеп геометрия курсында ұқсас түрлендіру әдісіне есептер шығару барысы.
Зерттеу пәні - мектепте геометрияны оқыту әдістемесі.
Жұмыстың негізгі мақсаты - ұқсас түрлендіру әдісіне есептер шығару жолдарын айқындау және есептер шығаруда назар аудару керек болатын жалпы әдістемелік ережелерді жасау.
Болжам: ұқсас түрлендіру әдісіне есептер шығаруды үйрету жоғары дәрежеде болады, егер:
1) ұқсас түрлендіру әдісіне есептер шығаруды үйретуден бұрын қарапайым салу есептерімен жеткілікті жұмыс жүргізілетін болса;
2) Салу есептері тек қана өзіндік нысан ретінде ғана емес, сондай-ақ декарттық координат жүйесінің элементі ретінде де қарастырылады;
3) ұқсас түрлендіру әдісіне есептер шығару, салу есептерін жақсы меңгергеннен соң орындалады;
Зерттеудің міндеттері:Зерттеудің проблемасын шешу, болжамның дұрыстығына көз жеткізу және мақсатқа жету үшін келесі мәселелер орындалады:
- осы тақырып бойынша ғылыми-әдістемелік әдебиеттерді зерттеу;
- заманауи оқу құралдарына осы тақырыптың баяндалуына логикалық дидактикалық талдау жүргізу;
- алынған мәліметтерді жалпылау және жүйелеу;
- жасалынған әдістемені пайдаланудың тиімділігін есептер шығаруда тексеру;
Зерттеу әдістері:Жұмыстың мақсатына жету, болжамды тексеру және жоғарыда қойылған мәселелерді шешу үшін келесі әдістер пайдаланылды:
- мектепте геометрияны оқытуға қатысты бағдарламаларды, оқу құралдарын, әдістемелік материалдарды үйрену;
- әртүрлі авторлық мектеп оқулықтарын салыстырмалы талдау арқылы жұмыс тақырыбына сай материалдарды жинақтау, сұрыптау;
- озат мұғалімдердің іс-тәжірибелерімен танысу, зерделеу;
- сабақ үстінде оқушылардың іс-әрекеттерін бақылау.
Жұмыстың құрылымы:кіріспеден, екі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен құралған.
1 Ұқсас түрлендірудің теориялық мәні
1. 1 Ұқсастық түрлендірудің негізгі әдістері
Шамалардың біртектілігін сараптау және теңдеулерді сараптау әдістерінің айырмашылығы - олардың физикалық қасиеттері мен құбылыстарын жете білуде болып табылады. Бірінші жағдайда шамалар біртектілігіне талдау жасау физикалық шамалардың біртектілігі формулаларына да қолданылады, екінші жағдайда - шамалар арасындағы аналитикалық байланысқа қолданылады.
Бұл бөлімде геометриялық модельдер мен натуралардың физикалық теңдеулер арөылы алыну мысалдары көрсетілген. Бұл жоба бойынша теңдеулерге талдама жасау әдісі біртекті шамаларды талдау әдісімен жақындастырылып, ұқсастықтың классикалық теориясымен сай келеді. Фигуралардың ұқсастығы жайлы ғылым б. э. дейін Ү-ІҮ ғ. ғ. Гиппократ Хиосскийдің, Архит Таренскийдің, Евдокс Книдский т. б. еңбектерінде жарық көрген. Ол Евклидтің ҮІ «Бастау» кітабында да баяндалды. Қасиеттері. Ұқсастық евклид кеңістігінің өзіне бейнеленуі.
Ұқсастық түзу бойындағы нүктелер ретін мақтайды, яғни егер нүкте нүктелер арасында жатса, және, , - олардың сай келетін бейнелері де сол нүктелер арасында жатады . және .
Бір нүктеде жатпайтын нүктелер, кез келген ұқсастықта бір түзу бойында жатпайтын нүктелерге ауысады.
Ұқсастық түзуді түзуге, кесіндіні кесіндіге, сәулені сәулеге, бұрышты бұрышқа, бұрышты бұрышқа, шеңберді шеңберге айналдырады.
Ұқсастық кезінде бұрыш өз шамасын сақтайды.
Ұқсастық өзіндік (өзіндік емес) деп аталынады, егер қозғалыс өзіндік (өзіндік емес) болса. Өзіндік ұқсастық фигуралар ориентациясын сақтайды, ал өзіндік емес - оны қарама-қарсыға өзгертеді.
Екі үшбұрыш бір- біріне ұқсас болып келеді, егер
- Олардың бұрыштары тең болса немесе жақтары пропорционал болса.
- Ұқсас фигуралар ауданы оларға ұқсас сызықтар квадратына пропорционал (мысалы, жақтарының) . Шеңбер аудандары олардың квадраттарының диаметрлеріне қатысты пропорционал (немесе радиустарына) .
- Белгілеу
Ұқсастықтарды белгілеу үшін ~белгісі қолданылады.
1. 2 Ұқсас түрлендіру анықтамасы
Ұқсас түрлендіру анықтамасы қозғалыстың анықтамасына ұқсас: егер F фигураның Ғ 1 фигурасына түрлендіру кезінде нүктелер арасындағы қашықтық бір санға бірнеше есе өссе, немесе кемісе, онда ол ұқсас түрлендіру деп аталады. Демек, F фигурасының кез келген A және В нүктелері түрлендіру кезінде F 1 фигурасының сәйкесінше А 1 және В 1 нүктелеріне ауысса, онда А 1 В 1 = кАВ, к саны ұқсастық коэффициенті деп аталады.
Ұқсас түрлендірудің анықтамасын енгізген соң, гомотетия ұқсас түрлендіру болатындығы дәлелденеді. Теорема координаттар әдісін қолдану арқылы дәлелденеді. Центрі О нүктесі, коэффициенті к болатын гомотетия аламыз.
Координат жүйесін оның бас нүктесі гомотетия центрімен дәл келетіндей етіп таңдап аламыз. А. В. Погореловтың оқулығында бірдей ұқсас фигуралардың анықтамасы беріледі, содан соң үшбұрыштардың ұқсастығы қарастырылады.
А. С. Атанасянның және т. б. оқулығында әуелі ұқсас көпбұрыштаp оқытылады, содан соң ұқсас фигуралардың жалпы анықтамасы беріледі. Жалпы алғанда, түрлі оқулықтардағы ұқсас фигуралар анықтамаларының бір-бірінен айтарлықтай алшақтығы жоқ: «Егер Ғ және Ғ 1 екі фигуралары бір-біріне ұқсас түрлендірулер арқылы көшетін болса, онда олар ұқсас деп аталады».
Ұқсас түрлендірулер қасиеттерінен, ұқсас көпбұрыштардың сәйкес бұрыштары тең, ал сәйкес қабырғалары пропорционал екендігі шығады. Жеке алғанда, ABC және A
1
B
1
C
1
ұқсас үшбұрыштарында
 A=
A=
 A
1
,
A
1
,
 В=
В=
 В
1
,
В
1
,
 С=
С=
 С
1
,
С
1
,
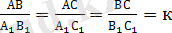 ;
;
Үшбұрыштардың ұқсастық белгілерін тұжырымдайық:
1) Егер бір үшбұрыштың екі бұрышы, екінші үшбұрыштың сәйкес екі бұрышына тең болса;
2) Егер біреуінің екі қабырғасы, екіншісінің сәйкес екі қабырғасына пропорционал, ал олардың арасындағы бұрыштар тең болса;
3) Егер бір үшбұрыштың қабырғалары, екінші үшбұрыштың қабырғаларына пропорционал болса, онда ол үшбұрыштар ұқсас болады.
Бұл белгілер гомотетияны қолдану арқылы жиі дәлелденеді.
Бірінші дәлелдеудің сатыларын көрсетейік:
1) Центрін қалауымызша алып, к коэффициентімен ∆А 1 В 1 С 1 үшбұрышына үшін гомотетия орындаймыз. Гомотетия нәтижесінде алынған үшбұрышты А 2 В 2 С 2 деп белгілейміз.
2) ∆А 2 В 2 С 2 = ∆АВС және ∆ А 2 В 2 С 2 = ∆А 1 В 1 С 1 екендігі дәлелденеді.
3) ∆А 1 В 1 С 1 үшбұрышы ABC үшбұрышынан ұқсас түрлендіру және қозғалыс нәтижесінде алынғандықтан, олар ұқсас болады.
к - гомотетияның берілген коэффициенті.
Кез келген ( х; у ) нүктесі ( кх; ку ) нүктесіне көшетіндей түрлендіру қарастырамыз, осы түрлендірудің гомотетия екендігін дәлелдейміз.
Қандай да болмасын f фигурасының кез келген А( х 1 , у 1 ) нүктесін алайық, ол А 1 ( кх 1 ; ку 1 ) нүктесіне ауысады.
ОА түзуі координат басынан өтеді, демек оның теңдеуі ах+ву= 0 түрінде болады. Ол А нүктесінің координаталарын қанағаттандырады, яғни ах 1 + ву 1 =0. А 1 нүктесінің де координаталары да осы теңдеуді көрсетейік:
а ( кх 1 ) + в(к у 1 ) = к ( ах 1 + ву 1 ) = к ∙0 =0,
Демек, А 1 нүктесі де ОА түзуінде жатады.
ОА=
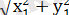 , ОА
1
=
, ОА
1
=
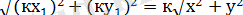 .
.
Онда, ОА=к∙ОА 1 ол гомотетия анықтамасы бойынша біздің түрлендіру центрі О нүктесі, коэффициент к болатын гомотетия.
Осы түрлендірудің ұқсас түрлендіру болатындығын дәлелдейік. Ол үшін A 1 B 1 = к∙АВ екендігін көрсетеміз. Мұндағы А және В - берілген нүктелер, ал А 1 және В 1 нүктелері осы гомотетияда А және В нүктелері көшетін нүктелер.
Қозғалыстағы сияқты ұқсас түрлендіру кезінде бір нүктеде жататын A, В, С нүктелері, бір түзуде жататын А 1 В 1 С 1 нүктелеріне көшеді. Егер В нүктесі А және С нүктелерінің арасында жатса, онда В 1 нүктесі А 1 және С 1 нүктелерінің арасында жатады. Бұдан ұқсас түрлендіру кезіңде түзудің түзуге, жарты түзудің жарты түзуге, кесіндінің кесіндіге көшіретіндігі шығады.
Гомотетияны қолдану арқылы ұқсас түрлендіру кезінде сәулелер арасындағы бұрыштардың өзгермейтіндігі дәлелденеді.
Ұқсастық түрлендіру жәрдемімен ұқсас фигуралар ұғымына анықтама беріледі.
Геометрия курстарында ұқсас фигуралар ұғымы қарастырылады. Кейде ұқсас фигуралардың жалпы анықтамасы мүлдем берілмейді, тек үшбұрыштар мен көпбұрыштардың ұқсастығы қарастырылады.
Кеңістіктегі гомотетия және ұқсас түрлендіру жазықтықтағы секілді анықталады. Кеңістіктегі гомотетия ұқсас түрлендіру болатындығы дәл осылай дәлелденеді [20] .
Теорема 1 . Егер бір үшбұрыштың екі бұрышы екінші үшбұрыштың eкі бұрышына тең болса, ондай үшбұрыштар ұқсас болады.
Д ә л е л д е у
. Айталық, ABC және А
1
В
1
С
1
үшбұрыштарында
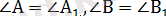 болсын. Сонда, ∆ABC
∞ ∆
А
1
В
1
С
1
болатынын дәлелдейміз.
болсын. Сонда, ∆ABC
∞ ∆
А
1
В
1
С
1
болатынын дәлелдейміз.
Айталық,
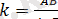 болсын. А
1
В
1
С
1
үшбұрышына ұқсастық
болсын. А
1
В
1
С
1
үшбұрышына ұқсастық
коэффициенті k болып келген қандай да бip ұқсас түрлендіруді, мысалы гомотетияны қолданайық (9-сурет) . Сонда АВС үшбұрышына тең қандай да бip A
2
В
2
C
2
үшбұрышы шығады. Шынында да, ұқсас түрлендіру бұрыштарды сақтап қалдыратындықтан,
 болады. Олай болса, АВС және A
2
В
2
C
2
үшбұрыштарында
болады. Олай болса, АВС және A
2
В
2
C
2
үшбұрыштарында
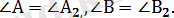 Әрі қарай,
Әрі қарай,
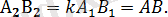 Олай болса, ABC және A
2
В
2
C
2
үшбұрыштары екінші белгі бойынша (қабыр- ғасы мен оған іргелес жатқан бұрыштары бойынша) тең болады.
Олай болса, ABC және A
2
В
2
C
2
үшбұрыштары екінші белгі бойынша (қабыр- ғасы мен оған іргелес жатқан бұрыштары бойынша) тең болады.
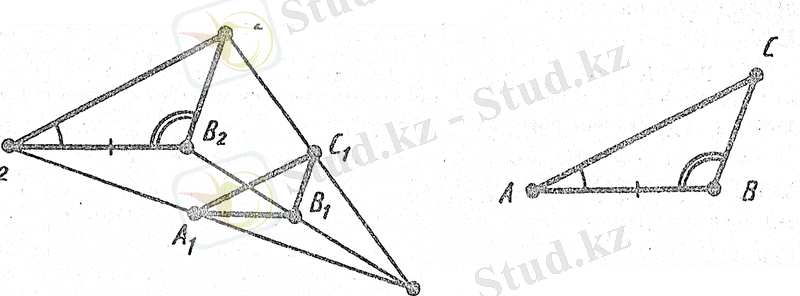
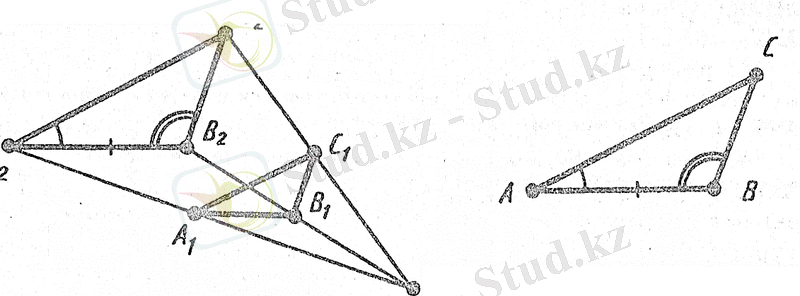
1-сурет
1 В 1 С 1 және A 2 В 2 C 2 үшбұрыштары гомотетиялы, ендеше, ұқсас болатындықтан, ал A 2 В 2 C 2 және ABC үшбұрыштары тең және сондықтан ұқсас болатындықтан А 1 В 1 С 1 және ABC үшбұрыштары ұқсас болады. Теорема дәлелденді [27] .
Есеп (1) . АВС үшбұрышының АВ қабырғасына параллель жүргізілген түзу оның АС қабырғасын A 1 нүктесінде, ал ВС қабырғасын В 1 нүктесінде қиып өтеді. Сонда ∆АВС ∞ ∆А 1 В 1 С 1 болатынын дәлелдеңдер.
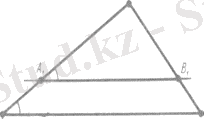
2-сурет
Ш е ш у i (2-сурет) . АВС және А 1 В 1 С 1 үшбұрыштарының С төбесіндегі бұрышы ортақ, алСА 1 В 1 және CAB бұрыштары тең, өйткені оларАВменА 1 В 1 параллель түзулерін AC түзyi қиып өткенде шығатын сәйкес бұрыштар. Олай болса, eкi бұрышы бойынша∆АВС ∞ ∆А 1 В 1 С 1 болады.
1. 3 Үшбұрыштардың екі қабырғасы және олардың арасындағы бұрышы бойынша ұқсастық белгісі
Теорема2. Егер бір үшбұрыштың eкi қабырғасы екінші үшбұрыштың қабырғасына пропорционал болып және осы қабырғалар жасайтын бұрыштар тең болса, ондай үшбұрыштар ұқсас болады [4] .
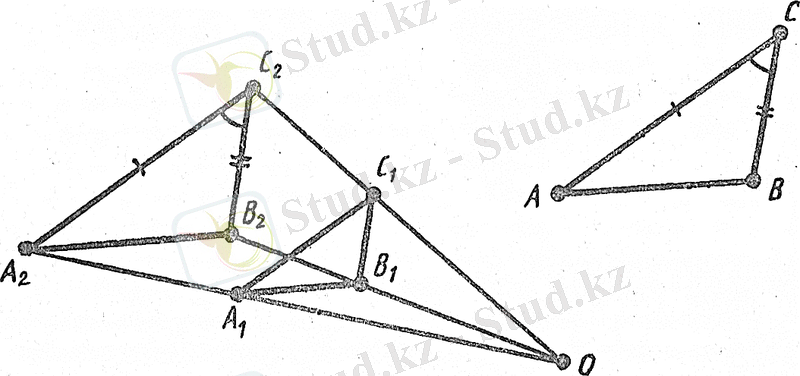
3-сурет
Д ә л е л д е у
. (3 теореманың дәлелдеуіне ұқсас дәлелденеді) . Айталық, АВС және А
1
В
1
С
1
үшбұрыштарында
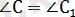 және AC = kA
1
C
1
, BC = kB
1
C
1
болсын. Сонда ∆АВС ∞ ∆А
1
В
1
С
1
болатындығын дәлелдейміз.
және AC = kA
1
C
1
, BC = kB
1
C
1
болсын. Сонда ∆АВС ∞ ∆А
1
В
1
С
1
болатындығын дәлелдейміз.
А
1
В
1
С
1
үшбұрышына коэффициенті kұқсас түрлендіруді, мысалы (гомотетияны, қолданамыз (11-сурет) . Сонда ABC үшбұрышына тең болатын қандай да бip A
2
В
2
C
2
үшбұрышы шығады. Шынында да, ұқсас түрлендіру бұрыштарды сақтап қалдыратындықтан,
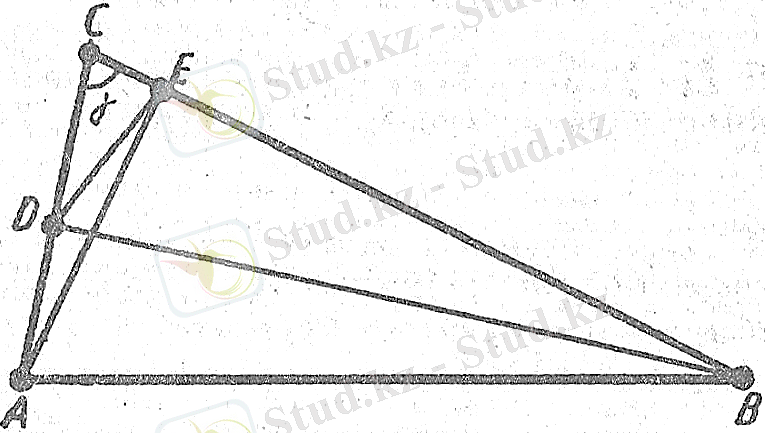
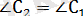 болады. Демек, ABC мен A
2
В
2
C
2
үшбұрыштарының
болады. Демек, ABC мен A
2
В
2
C
2
үшбұрыштарының
 болады. Әpi қарай A
2
C
2
= kA
1
C
1
= AC, В
2
С
2
꞊ kВ
1
С
1
=BC. Олай болса, ABC және A
2
В
2
C
2
үшбұрыштары бipiншi белгі (eкi қабырғасы және олардың арасындағы бұрышы) бойынша тең болады.
болады. Әpi қарай A
2
C
2
= kA
1
C
1
= AC, В
2
С
2
꞊ kВ
1
С
1
=BC. Олай болса, ABC және A
2
В
2
C
2
үшбұрыштары бipiншi белгі (eкi қабырғасы және олардың арасындағы бұрышы) бойынша тең болады.
4-сурет
А 1 В 1 С 1 және A 2 В 2 C 2 үшбұрыштары гомотетиялы, ендеше ұқсас болатындықтан, ал A 2 В 2 C 2 және ABС үшбұрыштары тең, сондықтан бұлар да ұқсас болғандықтан, А 1 В 1 С 1 және АВС үшбұрыштары ұқсас болады. Теорема дәлелденді [4] .
Есеп (2) . С бұрышы сүйір болып келген ABC үшбұрышының АЕ мен BDбиіктіктері жүргізілген. (12 - сурет) . Сонда ∆ABC ∞ ∆EDC болатынын дәлелдеңдер.
Ill е ш у i. ABC мен EDC үшбұрыштарының С төбесіндегі бұрыш екеуіне ортақ. Осы бұрышпен іргелес жатқан қабырғалардың пропорционал болатынын дәлелдейік. Сонда, ЕС꞊AСcosγ, DC꞊ВС cosγ . Яғни үшбұрыштардың Сбұрышына іргелес жатқан қабырғалары пропорционал болады. Демек, eкi қабырғасы мен олардың арасындағы бұрышы бойынша ∆ABC ∞ ∆EDC болады.
2 Мектеп геометрия курсындағы ұқсас түрлендіру бойынша есеп шығару ерекшеліктері
2. 1 Ұқсас түрлендірулердің есептері
Шеңбер. Шеңбер деп берілген нүктеден бірдей қашықтықта жатқан жазықтықтың барлық нүктелерінен тұратын фигураны айтады. Берілген нүкте шеңбердің центрі деп аталады.
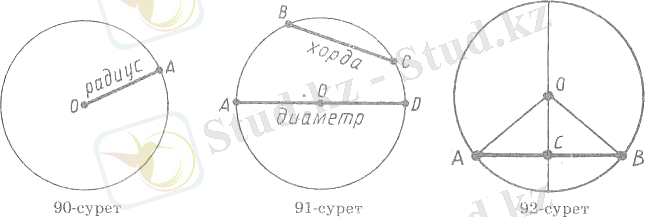
Шеңбер нүктелерінен оның центріне дейінгі ара қашықтық шеңбердің радиусы деп аталады. Радиус деп, сондай-ақ шеңбер нүктесін оның центрімен қосатын кез келген кесіндіні айтады (4-сурет) .
Шеңбердің екі нүктесін қосатын кесінді хорда деп аталады. Центр арқылы өтетін хорда диаметр деп аталады. 5-суреттегі ВС - хорда, AD- диаметр.
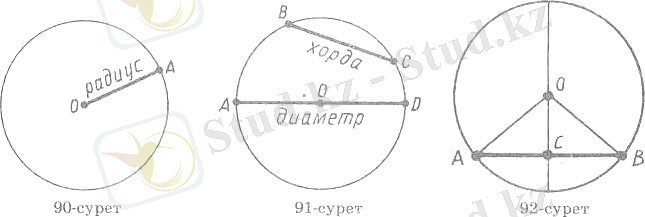
4-сурет
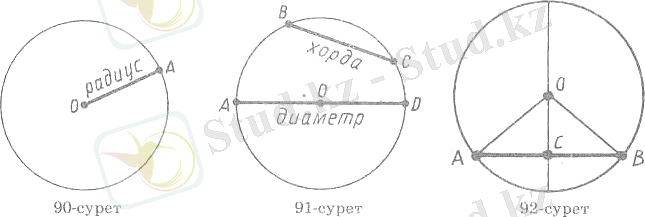
5-сурет
6-сурет
Есеп (3) . Хорданың ортасы арқылы өтетін диаметр хордаға перпендикуляр болатынын дәлелдеңдер.
Шешуі. АВ - шеңбердің хордасы, ал С- оның ортасы болсын (6-сурет) . АОВ- табаны АВболатын тең бүйірлі үшбұрыш. Оның ОА және ОВқабырғалары шеңбердің радиустары болғандықтан тең. Тең бүйірлі үшбұрыш -тың табанына жүргізілген медианасының қасиеті бойынша ОС кесіндісі биіктік болып табылады. Сондықтан хорданың ортасы арқылы өтетін диаметр хордаға перпендикуляр болады
Үшбұрышқа сырттай сызылған шеңбер
Егер шеңбер үшбұрыштың барлық төбелері арқылы өтсе, онда ол үшбұрышқа сырттай сызылған шеңбер деп аталады.
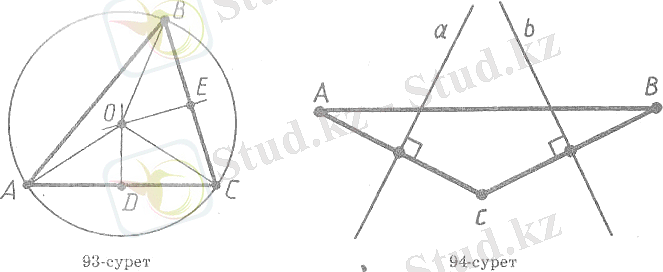
Теорема 3 . Үшбұрышқа сырттай сызылған шеңбердің центрі үшбұрыш қабырғаларының орталары арқылы жүргізілген перпендикулярдың қиылысу нүктесі болып табылады.
7-сурет
8-сурет
Дәлелдеу . Айталық ABC - берілген үшбұрыш және О - оған сырттай сызылған шеңбердің центрі болсын (7-сурет) . АОС үшбұрышы тең бүйірлі: оның ОАмен ОСқабырғалары радиустар болғандықтан тең. Бұл үшбұрыштың OD медианасы оның биіктігі де болып табылады. Сондықтан шеңбердің центрі АСқабырғасына перпендикуляр әрі оның ортасынан өтетін түзудің бойында жатады. Дәл осылайша шеңбердің центрі үшбұрыштың қалған екі қабырғасының да перпендикулярында жататыны дәлелденеді. Теорема дәлелденді [17] .
Ескерту. Кесіндінің ортасы арқылы өтіп және оған перпендикуляр болатын түзуді көбінесе орта перпендикуляр деп атайды. Осыған байланысты кейде былай дейді: үшбұрышқа сырттай сызылған шеңбердің центрі үшбұрыш қабырғаларының орта перпендикулярының қиылысу нүктесінде жатады.
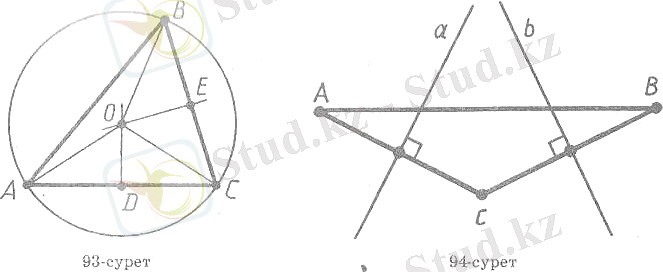
Есеп (4) . Үшбұрыштың екі қабырғасының орта перпендикуляры қиылысатынын дәлелдеңдер.
Ш е ш у і. Айталық, ABC - үшбұрыш, ал а және b - оның АС және ВС қабырғаларының орта перпендикуляры болсын (8-сурет) . а жөне b түзулері қиылыспайды, яғни параллель деп жориық. АСтүзуі а түзуіне перпендикуляр. ВСтүзуі b түзуіне перпендикуляр, демек, ол a түзуіне де перпендикуляр, өйткені а және b түзулері параллель. Сонымен АС және ВС түзулерінің екеуі де а түзуіне перпендикуляр, олай болса, олар параллель. Ал бұл дұрыс емес. АС және ВСтүзулері С нүктесінде қиылысады. Біз қайшылыққа келдік. Пікір дәлелденді [17] .
Шеңберге жанама
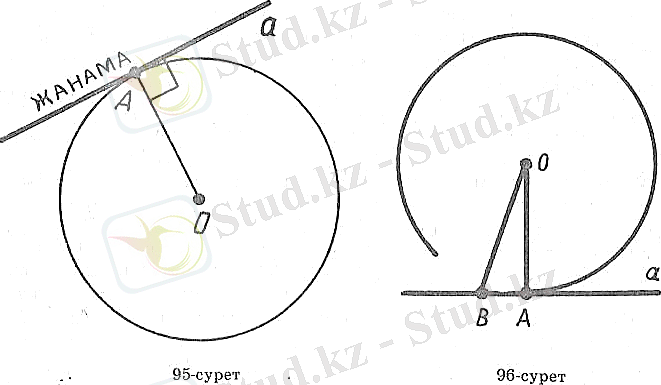
Шеңбердің бір нүктесі арқылы өтіп және осы нүктеге жүргізілген радиусқа перпендикуляр болатын түзу жанама деп аталады. Шеңбердің берілген нүктесі жанасу нүктесі деп аталады.
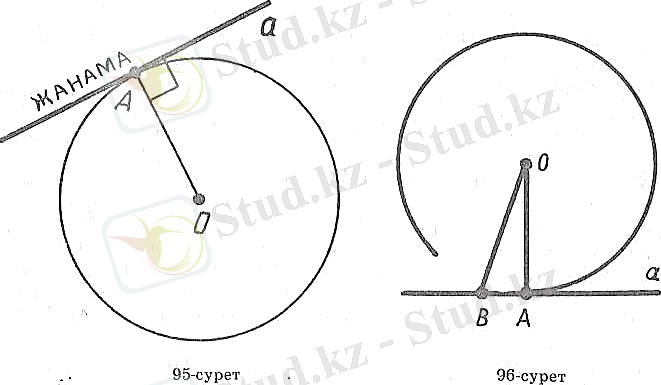
9-суретте а түзуі шеңбердің Анүктесі арқылы ОА радиусына перпендикуляр болып өтеді. а түзуі шеңберге жанама болып табылады. А нүктесі жанасу нүктесі болып табылады. Былай айтуға да болады: шеңбер а түзуін А нүктесінде жанайды.
9-сурет
10-сурет
Есеп (5) . Шеңбер мен жанаманың жанасу нүктесінен басқа ортақ нүктесі жоқ екенін дәлелдеңдер.
Шешуі. a - шеңберге А нүктесінде жүргізілген жанама болсын (10-сурет) . Жанама мен шеңбердің А нүктесінен өзге тағы бір ортақ нүктесі В бар деп жориық. АОВ- табаны АВболатын тең бүйірлі үшбұрыш болады. Оның ОАжәне ОВ қабырғалары - шеңбердің радиустары. Тең бүйірлі үшбұрыштың табанындағы бұрыштары тең, ал Атөбесіндегі бұрышы тік болғандықтан, бұл үшбұрыштың екі тік бұрышы бар болады. Ал, бұл мүмкін емес. Біз қайшылық -қа келдік. Пікір дәлелденді.
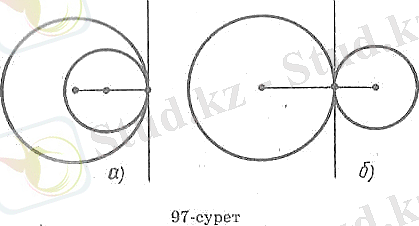
11-сурет
Ортақ нүктесі бар екі шеңбердің осы нүктеде ортақ жанамасы бар болса, шеңберлер осы нүктеде жанасады дейді (11- сурет) . Егер шеңберлердің центрлері ортақ жанаманың бір жағында жатса, онда жанасу іштей жанасу деп аталады (11, а - сурет) . Егер шеңберлердің центрлері ортақ жанаманың әр жағында жатса, онда жанасу сырттай жанасу деп аталады (11, б-сурет) .
Салу есептерін шешуде пайдаланылатын геометриялық орындар әдісінің мәнісі мынада. Айталық, салу есебін шешкенде екі шартты бірдей қанағаттандыратын X нүктесін табу керек болсын. Бірінші шартты қанағаттандыратын нүктелердің геометриялық орны қайсыбір Ғ 1 фигурасы болады, ал екінші шартты қанағаттандыратын нүктелердің геометриялық орны қайсыбір Ғ 2 фигурасы болады. Ізделінді X нүктесі Ғ 1 фигурасына да, Ғ 2 фигурасына да тиісті, яғни олардың қиылысу нүктесі болып табылады.
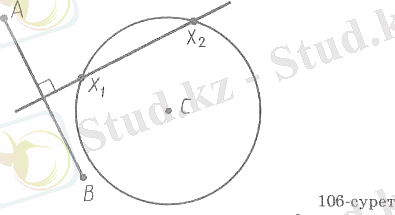
12-сурет
Егер бұл геометриялық орындар қарапайым болса (мысалы, түзулер мен шеңберлерден тұрса), біз оларды сала аламыз және қажетті X нүктесін тауып алуымызға болады. Мысал келтірейік.
Есеп (6) . A, В, С үш нүкте берілген, А және В нүктелерінен бірдей қашықтықта және С нүктесінен берілген қашықтықта X нүктесін табу керек.
Ш е ш у і . Ізделінді X нүктесі екі шартты қанағаттандырады:
1) ол А мен В нүктелерінен бірдей қашықтықта жатады;
2) ол С нүктесінен берілген қашықтықта жатады.
Бірінші шартты қанағаттандыратын нүктелердің геометриялық орны - АВкесіндісіне перпендикуляр әрі оның ортасынан өтетін түзу (12-сурет) . Екінші шартты қанағаттандыратын нүктелердің геометриялық орны - центрі С нүктесінде, ал радиусы берілген ара қашықтыққа тең болатын шеңбер. Ізделінді X нүктесі осы геометриялық орындардың қиылысуында жатады.
Есеп (7) . Ұқсас үшбұрыштар периметрлерінің қатынасы олардың сәйкес қабырғаларының қатынасындай болатындығын дәлелдеңдер.
Шешуi : Айталық, ABC және А 1 В 1 С 1 - ұқсас үшбұрыштар болсын. Сонда А 1 В 1 С 1 үшбұрышының қабырғалары ABC үшбұрышының қабырғаларына пропорционал болады, яғни A 1 В 1 = kAB, В 1 С 1 ꞊ k ВС, А 1 С 1 = kАС. Осы теңдіктерді мүшелеп қоссақ, шығатыны:
A 1 В 1 + В 1 С 1 + А 1 С 1 = k(AB+ ВС +АС) .
Бұдан
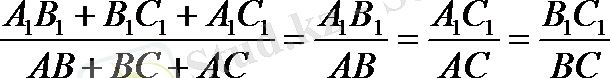 ,
,
яғни үшбұрыштардың периметрлерінің қатынасы олардың сәйкес қабырғаларының қатынасындай болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz