Зат бөлшектерінің толқындық қасиеттері: де-Бройль жорамалы мен оның тәжірибелік расталуы


Бөлшектердің толқындық қасиеттері"
1. Бөлшек күйін кванттық механикада бейнелеу. Толқындық функция. Суперпозиция принципі
2. Микробөлшектердің толқындық қасиеттері және аны қталмаушылық қатынасы.
3. Зат бөлшектерінің толқындық қасиеттері. Де Бройль жорамалы
4. Зат бөлшектері толқындық қасиеттерінің тәжірибеде расталуы
Қорытынды
Пайдаланылған әдебиеттер
Кіріспе
Зат бөлшектерінің толқындық қасиеттері жайындағы де-Бройль идеясын дамыта келе, австрия физигі Э. Шредингер өзінің атақты теңдеуін ұсынды (1926) . Осы теңдеу әр түрлі күш өрістерінде қозғалатын бөлшектің толқындық функцияларын табуға мүмкіндік береді. Шредингер теңдеуі былай жазылады:
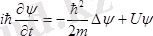 , (1)
, (1)
мұндағы т - бөлшек массасы, і - жорамал бірлік, U - бөлшектің потенциалдық энергиясы,
 - Лаплас операторы.
- Лаплас операторы.
Кез келген физикалық теория сияқты кванттық механика да кейбір постулаттарға негізделеді. Осы постулаттардың дұрыстығын кванттық механиканың болжауларын бөлшектердің толқындық қасиеттері ескерілетін эксперимент нәтижелерімен салыстырып растауға болады.
Кванттық механиканың бірінші постулаты:бөлшектің күйі кванттық механикада кеңістіктік координаттар және уақыттың функциясы болып табылатын Ψ толқындық функциямен бейнеленеді.
Корпускулалық толқындық дуализмге сәйкес кванттық теорияда бөлшек күйі Ψ(r, t) -пси функциямен беріледі. Бұл комплекс функция және формальды түрде толқындық қасиеттерге ие.
1926 ж М. Борн кванттық механикадағы толқындық функцияның ықтималдық мағынасын былайша тұжырымдады:Ψ(x, y, z, t) толқындық функцияның модулінің квадраты берілген t≥0 уақыт мезетінде кеңістіктің координаты x, y, z M=M(x, y, z) нүктесінде бөлшектің табылу ықтималдығының ω тығыздығын анықтайды.
Бөлшектердің толқындық қасиеттері анық байқалған тәжіри-белерге америка физиктері К. Дэвиссон және Л. Джермер тәжірибелері жатады 1. Тәжірибе схемасы суреттерде көрсетілген. =500 және үдет-кіш кернеу U=54 В болғанда шағылған электрондардың әсіресе айқын максимумы байқалған.
1. Бөлшек күйін кванттық механикада бейнелеу. Толқындық функция. Суперпозиция принципі
Сәулелену кванттары - фотондардың екіжақты қасиеттері болады, оларды бірінші жағдайда корпускулалар (бөлшектер) ретінде, ал екінші жағдайда толқындар ретінде қарастыруға болады. Осы идеяны 1923-1924 жылдары нөлден өзгеше тыныштықтық массаға ие болатын бөлшектерге арнап қолданған де Бройль болды. Оның болжауынша, бұл бөлшектердің корпускулалық қасиеттерімен қатар толқындық қасиеттері де болады. Әрине, оның ғылыми болжамы сол кезде күтпеген өте батыл ой болды.
Де Бройль қатысын басқа да қарапайым әдіспен алуға болады. Оптика курсынан белгілі, толқындық түйдектің топтық жылдамдығы
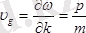
формуламен сипатталады.
Осыдан де Бройль қатысын аламыз (интегралдау тұрақтысын нөлге теңестірсе)
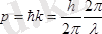
Бұл өрнекті үйреншікті түрде жазуға болады
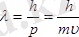
Осы қатыс де Бройль формуласы деген атпен белгілі.
Енді де Бройль толқынының физикалық мағынасына тоқталайық. Бөлшектердің толқындық қасиеттері болғандықтан, кванттық механиканың
 алғашқы даму барысында, бөлшекті толқындық түйдек түрінде қарастыру көрінісі басым болды. Толқындық теория бойынша, түйдектің өлшемі бөлшектің өлшемімен бірдей болады. Егер бөлшек ретінде еркін электронды алса, онда есептеулер бойынша толқындық түйдек
алғашқы даму барысында, бөлшекті толқындық түйдек түрінде қарастыру көрінісі басым болды. Толқындық теория бойынша, түйдектің өлшемі бөлшектің өлшемімен бірдей болады. Егер бөлшек ретінде еркін электронды алса, онда есептеулер бойынша толқындық түйдек
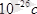 - тен кейін жайылып кетеді. Сонымен, еркін электронды толқындық түйдек түрінде қарастыру көрінісі дұрыс болмады, себебі электрон - тұрақты бөлшек. Де Бройль толқынына дұрыс мағына берген неміс физик - теоретигі Макс Борн болды. Оның айтуынша, егер бөлшек толқындық функциямен сипатталса, оның модулінің квадраты (яғни де Бройль толқынының қарқындылығы) кеңістіктің әр түрлі нүктелерінде бөлшекті табу ықтималдығын көрсетеді.
- тен кейін жайылып кетеді. Сонымен, еркін электронды толқындық түйдек түрінде қарастыру көрінісі дұрыс болмады, себебі электрон - тұрақты бөлшек. Де Бройль толқынына дұрыс мағына берген неміс физик - теоретигі Макс Борн болды. Оның айтуынша, егер бөлшек толқындық функциямен сипатталса, оның модулінің квадраты (яғни де Бройль толқынының қарқындылығы) кеңістіктің әр түрлі нүктелерінде бөлшекті табу ықтималдығын көрсетеді.
Классикалық физика көріністері бойынша, электронды зарядталған шарик ретінде қарастыруға болады. Ол шарик белгілі бір уақыт мезетінде қатаң анықталған орын алсын, яғни оның анықталған координаты болсын. Осы мезетте шарик анықталған импульске ие болады.
Кванттық теория көріністері бойынша, электрон толқындық қасиеттерге ие болады. Осы қасиеттердің негізінде біз бірмезетте электронның импульсін және координатын анықтай алмаймыз. Бұл пікірді Гейзенберг 1927 жылы мына түрде тұжырымдады: бөлшектің координаталарын және импульстерін бірмезетте дәл өлшеу мүмкін емес. Осы тұжырымдауды Гейзенбергтің анықталмағандықтар қатысы деп атайды.
Жалпы жағдайда бұл қатыс мына түрде жазылады :
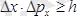 . (2. 3)
. (2. 3)
(2. 3) - Гейзенбергтің анықталмағандықтар қатысы деп аталынады. Бұл қатыс бойынша, егер
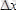 - бөлшектің
- бөлшектің
 координатын өлшеудегі қатесі болса, ал
координатын өлшеудегі қатесі болса, ал
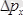 - оның
- оның
 өсі бағытындағы импульсін өлшеудегі қатесі болса, онда екі өлшеу қателерінің көбейтіндісі ешқашан да шаманың реті бойынша Планк тұрақтысынан кіші болмайды. Сонымен:
өсі бағытындағы импульсін өлшеудегі қатесі болса, онда екі өлшеу қателерінің көбейтіндісі ешқашан да шаманың реті бойынша Планк тұрақтысынан кіші болмайды. Сонымен:
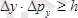 ,
,
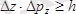 .
.
Планк тұрақтысы өте аз шама болғандықтан, анықталмағандықтар қатыстары макроденелер үшін білінбейді.
(2. 3) қатыс бойынша, егер координатаның мәні дәл анықталса
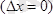 , онда импульстің мәні дәл анықталмайды
, онда импульстің мәні дәл анықталмайды
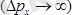 және керісінше.
және керісінше.
Гейзенбергтің анықталмағандықтар қатысын мына түрде де жазуға болады:
 . (2. 4)
. (2. 4)
Бұл қатыс бойынша, егер жүйенің энергиясы
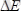 дәлдікпен өлшенсе, онда осы өлшеуге қатысты
дәлдікпен өлшенсе, онда осы өлшеуге қатысты
 уақыт минимальді анықталмағандыққа ие болады. (2. 3) және (2. 4) қатыстарын тағы да мынадай қатыстармен толықтыруға болады:
уақыт минимальді анықталмағандыққа ие болады. (2. 3) және (2. 4) қатыстарын тағы да мынадай қатыстармен толықтыруға болады:
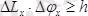 ,
,
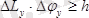 ,
,
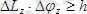 , (2. 5)
, (2. 5)
мұндағы
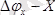 - өсьті айналдыра бұру бұрышының анықталмағандығы,
- өсьті айналдыра бұру бұрышының анықталмағандығы,
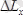 - бұрыштық моменттің х өсі бағытындағы анықталмағандығы. Сонымен, микродүниеде көп жағдайда физикалық шамалардың мәндері бірмезетте дәл анықталмайды.
- бұрыштық моменттің х өсі бағытындағы анықталмағандығы. Сонымен, микродүниеде көп жағдайда физикалық шамалардың мәндері бірмезетте дәл анықталмайды.
Де Бройль идеясы бойынша, бөлшектердің толқындық қасиеттері
болады. Осыған байланысты, кванттық механикаға мынадай постулат енгізуге болады: бөлшектің күйі толқындық функция
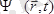 - мен сипатталады, оның модулінің квадраты t уақыт мезетінде координаты
- мен сипатталады, оның модулінің квадраты t уақыт мезетінде координаты
 - ға тең нүктеде табу ықтималдығының тығыздығын береді. Жалпы айтқанда, толқындық функция
- ға тең нүктеде табу ықтималдығының тығыздығын береді. Жалпы айтқанда, толқындық функция
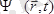 (пси-функция) комплекс функция болып саналады. Ол бөлшектің қозғалысын анықтайтын белгілі бір дифференциалдық теңдеуді қанағаттандырады. Мысалы,
(пси-функция) комплекс функция болып саналады. Ол бөлшектің қозғалысын анықтайтын белгілі бір дифференциалдық теңдеуді қанағаттандырады. Мысалы,
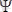 - функция кванттық механиканың негізгі теңдеуі Шредингер теңдеуінің шешімі болып табылады. Толқындық функция бөлшекті табу ықтималдығын анықтайтын көмекші комплекс шама, сондықтан оның тікелей физикалық мағынасы болмайды. Табу ықтималдығы нақты оң шама болу керек,
- функция кванттық механиканың негізгі теңдеуі Шредингер теңдеуінің шешімі болып табылады. Толқындық функция бөлшекті табу ықтималдығын анықтайтын көмекші комплекс шама, сондықтан оның тікелей физикалық мағынасы болмайды. Табу ықтималдығы нақты оң шама болу керек,
пси - функцияның модулінің квадраты бұл шартты қанағаттандырады.
Ақырсыз кішкене аймақ
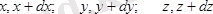 қарастырайық,
қарастырайық,
оның көлем элементін
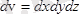
 деп белгілейік. Ықтималдық теориясы бойынша
деп белгілейік. Ықтималдық теориясы бойынша
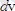 көлемдегі бөлшекті табу ықтималдығы мынаған тең:
көлемдегі бөлшекті табу ықтималдығы мынаған тең:
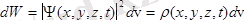 , (3. 1)
, (3. 1)
мұндағы
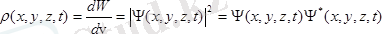 (3. 2)
(3. 2)
ықтималдық тығыздығы деп аталынады. Енді t уақыт мезетінде v көлемдегі табу ықтималдығын қарастырамыз:
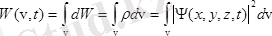 . (3. 3)
. (3. 3)
Бұл өрнек шын оқиғаның ықтималдығы. Ықтималдық теориясы бойынша шын оқиғаның ықтималдығы 1-ге тең деп қабылдауға тиістіміз. Егер осы келісімге тоқталсақ, (3. 3) -ті бірге теңестіреміз:
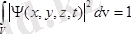 . (3. 4)
. (3. 4)
Сонымен біз нормалау шартын алдық. Осы шартты қанағаттандыратын
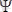 функциясы нормаланған функция деп аталынады.
функциясы нормаланған функция деп аталынады.
Толқындық функция келесі шарттарды қанағаттандырады.
1.
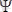 функция үзіліссіз болады және оның туындысы да үзіліссіз болу керек, себебі зарядтың және токтың тығыздығы үзіліссіз шамалар (ол шамалар толқындық функцияның көмегімен табылады) .
функция үзіліссіз болады және оның туындысы да үзіліссіз болу керек, себебі зарядтың және токтың тығыздығы үзіліссіз шамалар (ол шамалар толқындық функцияның көмегімен табылады) .
2.
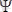 функция кеңістікте ақырлы және бірмәнді болу керек. Оның ақырлы болуы (3. 4) -ті қанағаттандырады және бірмәнділігі бастапқы мезеттегі толқындық функцияның мәні белгілі болса, кейінгі мезеттегі мәнін табуға болатындығын көрсетеді.
функция кеңістікте ақырлы және бірмәнді болу керек. Оның ақырлы болуы (3. 4) -ті қанағаттандырады және бірмәнділігі бастапқы мезеттегі толқындық функцияның мәні белгілі болса, кейінгі мезеттегі мәнін табуға болатындығын көрсетеді.
3.
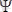 функция белгілі бір шекаралық шарттарды қанағаттандырады, себебі кванттық теңдеулердің шешімі математикалық физиканың кейбір есептерінің шешімін еске түсіреді. Егер осы үш шарт орындалса ғана толқындық функция кванттық теңдеудің жалғыз шешімі болып табылады.
функция белгілі бір шекаралық шарттарды қанағаттандырады, себебі кванттық теңдеулердің шешімі математикалық физиканың кейбір есептерінің шешімін еске түсіреді. Егер осы үш шарт орындалса ғана толқындық функция кванттық теңдеудің жалғыз шешімі болып табылады.
Классикалық физикада суперпозиция принципі жиі қарастырылады. Бұл принцип кванттық механикада да өте үлкен рөль атқарады, оның екі анықтамасы бар.
1. Егер жүйе
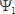 және
және
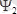 - мен сипатталатын күйлерде орналаса алса, онда ол осы екі функциялардың сызықтық комбинациясынан түзілген функциямен сипатталатын күйде де орналаса алады
- мен сипатталатын күйлерде орналаса алса, онда ол осы екі функциялардың сызықтық комбинациясынан түзілген функциямен сипатталатын күйде де орналаса алады
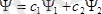 ,
,
мұндағы
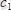 және
және
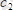 - кез келген комплекс сандар, олар
- кез келген комплекс сандар, олар

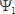 және
және
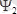 күйлердің амплитудаларын анықтайды.
күйлердің амплитудаларын анықтайды.
2. Егер толқындық функцияны кез келген нөлден өзгеше комплекс санға көбейтсек, онда жаңа толқындық функция жүйенің бастапқы күйіне сәйкес келеді.
Квантмеханикалық суперпозиция принципінің орындалуы үшін, қарастыратын теңдеулер сызықтық теңдеулер болуы керек. Егер күрделі күй бар болса, онда (4. 1) өрнек былай жазылады:
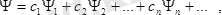
мұндағы
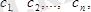 комплекс амплитудалар.
комплекс амплитудалар.
2 Микробөлшектердің толқындық қасиеттері және анықталмаушылық қатынасы .
Электрон әрі корпускулалық, әрі толқындық қасиеттері бар ерекше бөлшек, оның кейде корпускулалық, кейде толқындық қасиеттері білінеді; бұл сыртқы жағдайға байланысты. Әйтеуір электрон классикалық бөлшек емес. Сондықтан электронды (сондай-ақ әрбір элментар бөлшекті) макробөлшектерге тән физикалық шамалармен тек жуықтап қана сипаттауға болады. Осы жағдайға байланысты толқындық механикада мынадай принцип бар: элеткронның орнын және импульсін біл мезгілде дәл өлшеуге болмайды, басқаша айтқанда электронның координаттарын және жылдамдықтарын бір мезгілде дәл өлшеу мүмкін емес. Мысалы, электронның х координатасын өлшегендегі қателік
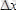 болып, оны осы х осі бағдарындағы жылдамдығын өлшегендегі қателік
болып, оны осы х осі бағдарындағы жылдамдығын өлшегендегі қателік
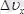 болса, онда
болса, онда
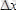 пен
пен
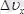 көбейтіндісінің шамасы Планк тұрақтысынан кем болмайды, яғни
көбейтіндісінің шамасы Планк тұрақтысынан кем болмайды, яғни
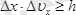 , дәлірек айтқанда
, дәлірек айтқанда
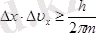 немесе
немесе
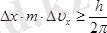 (6)
(6)
мұндағы
 - электронның массасы,
- электронның массасы,
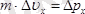 - импульсті өлшеудегі қателік болады, сонда:
- импульсті өлшеудегі қателік болады, сонда:
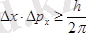 , (7)
, (7)
осылайша
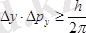
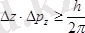 .
.
Осы (7) қатыстарды ең алғаш (1927 ж. ) неміс физигі Гейзенберг ұсынған болатын-ды, сондықтан бұлар Гейзенбергтің анықталмаушылық қатыстары деп аталады. Бұл қатысқа қарағанда, егер координатаның мәні дәл болса (мысалы
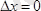 ), онда импульстің белгілі мәні болмайды (өйткені
), онда импульстің белгілі мәні болмайды (өйткені
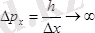 ), сондай-ақ импульстің мәні дәл болса (мысалы
), сондай-ақ импульстің мәні дәл болса (мысалы
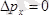 ), координатаның мәні болмайды (себебі
), координатаның мәні болмайды (себебі
 ) .
) .
Анықталмаушылық қатыстары заттың негізгі толқындық қасиеттерінен келіп шығады. Бұл қатыстар макрожүйелерге тән ұғымдарды микрожүйелерге қолдануға болмайтындығын көрсетеді.
3. Зат бөлшектерінің толқындық қасиеттері. Де Бройль жорамалы
Оптикалық құбылыстардың көпшілігін ( дифракция, интерференция)
жүйелі түрде толқындық көзқарас тұрғысынан кескіндеуге болатын оптика курсынан белгілі. Ал кейбір құбылыстарда (фотоэффект, Комптон эффект) жарық өзінің корпускулалық табиғатын анық байқатады.
Толқындық теория тұрғысынан қарағанда жарық
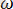 тербеліс жиілігі мен
тербеліс жиілігі мен
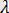 толқын ұзындығы арқылы сипатталады. Корпускулалық теория бойынша жарық фотонының
толқын ұзындығы арқылы сипатталады. Корпускулалық теория бойынша жарық фотонының
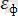 энергиясы,
энергиясы,
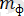 массасы мен
массасы мен
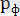 импульсы мынаған тең:
импульсы мынаған тең:
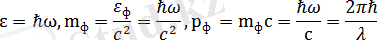
Сөйтіп жарық фотонының импульсы мен жарық толқыны ұзындығы арасындағы байланыс
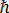 Планк тұрақтысы арқылы өрнектеледі.
Планк тұрақтысы арқылы өрнектеледі.
Француз ғалымы Луи де Бройль (1892-1987) жарықтың осы корпускулалық- толқындық табиғиты жөніндегі түсініктерді дамыта келе, 1924 ж. корпускулалық - толқындық дуализм тек оптикалық құбылыстарға тән ерекшелік емес, ол барлық микродүние физикасында жан - жақты қолданылуға тиіс деген батыл жорамал ұсынды.
Бөлшектердің корпускулалық және толқындық қасиеттерін сипаттайтын шамаларды байланыстыратын математикалық өрнектер дәл фотондардікі сияқты. Сонымен қозғалыстағы кез келген бөлшекпен бір толқындық процесс байланысқан болады.
Е
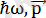
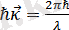 (3. 1)
(3. 1)
Оптикалық құбылыстар жағдайында (3. 1) өрнек фотон импульсын анықтау үшін пайдаланылады: фотон - тыныштық массасы нөлге тең. С жарық жылдамдығымен қозғалатын бөлшек. Осы қатынас, де - Бройльша, зат бөлшектеріне салыстырылатын жазық монохромат толқын ұзындығын береді.
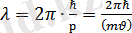 (3. 2)
(3. 2)
Тыныштық массасы нөл емес бөлшектер үшін р-
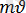 (3. 2. ) өрнектерді де - Бройль теңдеулері деп аталады. (3. 3. ) өрнегімен анықталатын толқын ұзындығы де - Бройль ұзындығыдеп аталады.
(3. 2. ) өрнектерді де - Бройль теңдеулері деп аталады. (3. 3. ) өрнегімен анықталатын толқын ұзындығы де - Бройль ұзындығыдеп аталады.
Де Борйль толқын ұзындығын энергияның функциясы ретінде табалық. Егер
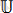 потенциалдар айырмасы әсерінен электрон
потенциалдар айырмасы әсерінен электрон
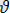 жылдамдыққа ие болса, онда оның
жылдамдыққа ие болса, онда оның
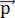 импульсы
импульсы
р
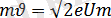
тең болады. Осы электронмен де Бройль толқыны байланысқан, оның толқын ұзындығы
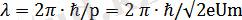 (3. 5)
(3. 5)
Электрон энергиясы Е
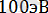 болсын. Осындай электрон үшін де Бройль толқын ұзындығын есептейік. Электрон жылдамдығы мына теңдіктен е
болсын. Осындай электрон үшін де Бройль толқын ұзындығын есептейік. Электрон жылдамдығы мына теңдіктен е
 -
-
 2 анықталады:
2 анықталады:
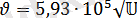
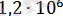 м/с
м/с
ал толқын ұзындығы
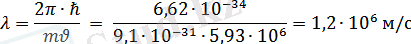
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz