Толқындық функция

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Мазмұны Кіріспе 1. Толқындық функция

2. Шредингер теңдеуін шешу мысалдары

3. Туннельдік эффект.

4. Дирак теңдеуі

Қорытынды

Пайдаланылған әдебиеттер тізімі

Кіріспе

Бұған дейін айтып кеткеніміздей, XX ғасырдың басында ашылған бірқатар құбылыстар мен тәжірибелік айғақтар классикалық физиканың негізгі келіп, оларды зерделеу нәтижесінде жаңа, кванттық көзқарас дами бастады. Микробөлшектердің корпускулалық-бөлшектік қасиеттерінің анықталуы, атомдық физика саласындағы зерттеулер классикалық физика заңдарын микробөлшектерге қолдануға қойылатын шектеулерді айқындады. Мұның өзі микробөлшектердің қозғалыс және өзара әсерлесу заңдарын сипаттайтын кванттық механиканың туындап, дамуына себепкер болды.

Релятивтік емес (баяу бөлшектерге арналған) кванттық механиканың негізгі теңдеуін 1926 жылы Э . Шредингер тұжырымдап жазды. Бұл теңдеуді біз қарастырмаймыз, тек оның негізгі сипаттамасы мен салдарларын талдау жеткілікті.

Бұл - толқындық теңдеу және одан тәжірибелерде бақыланатын бөлшектердің толкындық қасиеттері шығады. Кванттық механикада бөлшектің күйін толқындық функциямен сипаттайды. Толқындық функция - координаталар мен уақыттың комплекстік функциясы, оның айқын түрі Шредингер теңдеуінің шешуінен шығады да, соңында бөлшекке әрекет ететін күштердің сипатымен анықталады.

Кеңістіктің берілген нүктесіндегі де Бройль толқындарының интенсивтігі (амплитудасының квадраты) осы нүктеге түсетін бөлшектердің санын анықтайтыны туралы жоғарыда айтқанбыз. Ал, егер жеке бөлшек қарастырылса, оған сәйкес де Бройль толқынының интенсивтігі бөлшектің осы нүктенің маңына түсу ықтималдығынбілдіреді. Кванттық механиканың ең маңызды ерекшелігі - микробөлшектің күйін ықтималдылық тұрғысынан сипаттау. 1926 жылы М. Борн ықптималдық амплитпудасыдеп аталатын шама толкындық заңдылықпен өзгереді деген болжам айтты, бұл шаманы толқындың функция немесе ψ(пси) - функциясы деп атайды.

1. Толқындық функция

Кез келген фундаменталды физикалық теорияның құрылымында күй түсінігі және күй динамикасын түсіндіретін теңдеулер маңызды элементтер болып табылады.

Классикалық механикада бөлшектер күйі берілген уақыт мезетінде x, y, z координаттармен 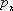, , 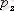импульстермен беріледі, ал динамиканың негізгі теңдеу - Ньютонның екінші заңы. Микродүние физикасында бөлшектер күйінің мұндай анықтамасы және күй функциясы болып табылатын күштер түсінігі мүлдем мағынасын жоғалтады.

Бөлшектердің толқындық қасиеттерінің болуы микробөлшектердің күйін, толқындық қасиеті бар қандай да бір функция көмегімен түсіндіруге болатынын айқындайды.

Кванттық механикада микробөлшектердің күйі кеңістіктік координаттар және уақыт функциясы болып табылатын 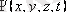толқындық функциямен беріледі. Релятивистік емес жағдайда бұл күйдің уақыт бойынша өзгеруі, яғни микробөлшектердің динмикасы кванттық теориялардың негізгі теңдеуі - Шредингер теңдеуімен сипатталады.

Толқындық функция математикалық мағынада өріс (ол комплексті болғандықтан 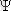функциясымен сипатталатын толқындар байқалмайды) болып табылады. Толқындық функцияның физикалық мағынасының түсініктемесін алғаш рет М. Борн берді, ол төменде келтірілген.

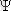комплексті функциясының 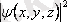модулының квадраты координаттары x, y, z болатын нүкте айналасындағы 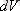көлемде бөлшектердің болу ықтималдығының тығыздығын береді. Микробөлшектерді t уақыт мезетінде осы көлем ішінде болу ықтималдығы келесі өрнекпен беріледі

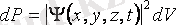. (11. 1)

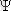функциясы өзінің мағынасы бойынша қандай да бір шарттарды қанағаттандыруы қажет. Толқындық функция барлық жерде үздіксіз және бірмәнд і болуы керек. Сонымен қатар (11. 1) өрнегімен анықталатын ықтималдық толқындық функцияның нормалдау шартына сәйкес бірге тең болуы тиіс.

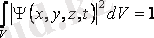. (11. 2)

Келтірілген шарттардың кванттық механикада үлкен мәні бар. Шредингер теңдеуінің шешімдері осы талаптарды тек белгілі бір шарттарында ғана, мысалы энергияның белгілі бір дискретті мәндерінде ғана қанағаттандырады.

Толқындық функция микробөлшектер күйінің негізгі сипаттамасы. Кванттық механикада толқындық функция арқылы осы күйдегі берілген объекті сипаттайтын физикалық шаманының орташа мәнін есептеуге болады.

Күйдің уақыт бойынша өзгеруі, яғни микробөлшектер динамикасы,

релятивистік емес жағдайда, кванттық теориялардың негізі болып табылатын Шредингердің стационар емес теңдеуімен сипатталады

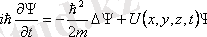, (11. 3)

мұндағы 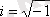- жорамал бірлік;

- бөлшек массасы;

- Лаплас операторы;

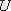- микробөлшектің потенциалдық энергиясы.

Бұл теңдеуді қандай да бір классикалық физиканың заңдарынан қорытылып шығарылмайды. Классикалық физикада Ньютонның екінші заңы қандай рөл атқарса, релятивистік емес кванттың механикада Шредингер теңдеуі дәл сондай рөл атқарады.

Кванттық механикада микробөлшек стационар күш өрісінде орналасқан және оның потенциалдық энергиясы уақытқа тәуелді емес болатын, стационар есептер көптеп кездеседі. Бұл жағдайда Шредингердің стационар теңдеуі қолданылады

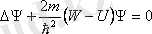. (11. 4)

Бұл теңдеудегі 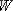параметрінің мағынасы бөлшектің толық энергиясы, ал бұл теңдеудің 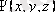шешімі кеңістіктік координатар функциясы болып табылады. Шредингер теңдеуі дербес туындылы теңдеу және оның шешімі үшін бастапқы және шекаралық шарттар берілуі қажет.

Берілген 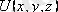жағдайда, (11. 4) теңдеуін қанағаттандыратын 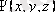функциясы меншікті функция , ал теңдеудің шешімінен шығатын 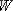энергия мәндері меншікті мәндер деп аталады.

Толқындық функцияның ықтималдық мағынасы.

Кез келген физикалық теория сияқты кванттық механика да кейбір постулаттарға негізделеді. Осы постулаттардың дұрыстығын кванттық механиканың болжауларын бөлшектердің толқындық қасиеттері ескерілетін эксперимент нәтижелерімен салыстырып растауға болады.
Кванттық механиканың бірінші постулаты:бөлшектің күйі кванттық механикада кеңістіктік координаттар және уақыттың функциясы болып табылатын Ψ толқындық функциямен бейнеленеді.
Корпускулалық толқындық дуализмге сәйкес кванттық теорияда бөлшек күйі Ψ(r, t) -пси функциямен беріледі. Бұл комплекс функция және формальды түрде толқындық қасиеттерге ие.

1926 ж М. Борн кванттық механикадағы толқындық функцияның ықтималдық мағынасын былайша тұжырымдады:Ψ(x, y, z, t) толқындық функцияның модулінің квадраты берілген t≥0 уақыт мезетінде кеңістіктің координаты x, y, z M=M(x, y, z) нүктесінде бөлшектің табылу ықтималдығының ω тығыздығын анықтайды. Демек,
ω=dp/dv=〖"Ψ" 〗^2 (1)
Осы өрнекті мына түрде жазамыз:
dp=〖"Ψ" 〗^2dv=Ψ*Ψdv (2)
мұндағы Ψ*-толқындық Ψ функциямен комплекс түйіндес функция, dp-бөлшектің берілген кванттық күйі үшін қайсыбір уақыт мезетінде бөлшектің М нүктесін қоршап тұрған dv элементар көлемінде табылу ықтималдығы.
(2) формуладан Ψ(x, y, z, t) толқындық функциямен бейнелетін берілген кванттық күйдегі бөлшекті кеңістіктің көлемі v шектеулі аймағында табу ықтималдығын да есептеуге болатындығы көрінеді. Шынында да
P=∫dp=∫_vωdv
болатындықтан, (1) және (2) ні ескеріп мына өрнекті аламыз:
P=∫_v 〖"Ψ" 〗^2dv немесе P=∫_vΨ*Ψdv (3)
Кванттық механикада (1) - (3) өрнектері толқындық функцияның ықтималдық мағынасын анықтайды.

Біз электронның корпускулалық қасиеті бар екендігін, яғни ол масса, энергия, импульс моменті, сызықты өлшемімен жəне т. б. қасиеттерімен сипатталатындығын білеміз. Сонымен қатар көптеген эксперименттік фактілер бойынша, электрон тек корпускулалық қасиетке ғана ие болып қоймайды, оның толқындық қасиеті де болатындығы анықталған болатын .

Толқындық (кванттық) механикада электронның қозғалысына байланысты толқындық қозғалыс қарастырылады. Ол қозғалыс - толқындық функциямен сипатталады, сонда бұл функция

кеңістіктің əрбір нүктесінде уақытқа байланысты монохроматты толқын түрінде сипатталады:

( x , y , z , t ) ₀ e

i

t ( k r )

мұндағы, E / немесе 2 ; мұндағы k - толқындық вектор, Е - бөлшектің стационар өрісте тұрақты болып қалатын толық энергия, n - толқын бетіне тұрғызылған нормаль.

(3. 1. 1)

формуладағы

( k r ) xk _x yk _y zk _z .

мұндағы

k _x , k _y , k _z

координаталар

бойынша толқындық

векторлар

компоненттері, олар

~ 77 ~

k _x

2

cos ; k _y

2

cos ; k _z

2

cos

(3. 1. 3)

kx:

cos ;ky:

cos ;kz:

cos:

(3. 1. 3):

мұндағы cos, cos, cos - толқын бетіне нормаль бойымен бағыттаушы косинустар.

Ал толқындық функцияның градиенті векторлық шама, олай болса:

ⁱ 0 _x

^j 0 _y

^k 0 _z

жəне оған Лаплас операторын қолдансақ, онда

2 ² ₂ ² ₂ ² ₂ x y z

мұндағы i ₀ , j ₀ , k ₀ координат осьтері бойымен алынған бірлік

векторлар. Онда (3. 1. 1) жазық монохрамат толқынның, уақыт бойынша өзгерісі:

i i ^E t

ал координат бойынша өзгерісі: 2 P ²

Энергияның сақталу заңы бойынша:

^{P

2} U ( x , y , z ) E

2 m

U ( x , y , z ) U ;

Шредингердің дифференциалдық теңдеуі деп аталады. Бұл микроəлемдегі сипатталатын негізгі кванттық механика процесі. Мұның шешуі атом энергиясының деңгейін, оған сəйкес келетін кванттық сандарды жəне сəулелену процесінде оның таралу облысындағы ерекше проблемеларды шешеді. (3. 1. 10) теңдік Шредингердің стационар теңдеуі деп аталады. Бұл теңдеу толқынның амплитудасы уақытқа тəуелді болмаған процесс кезінде қолданылады.

Шредингер теңдеуі электронның орбита бойымен қозғалуымен қатар, толқындық функция арқылы сипатталатын толқынның таралуын қарастырады. Толқындық функция электронның күйін сипаттайтын физикалық шарттың нақты түрін көрсетеді. Шредингер теңдеуі арқылы теңдеудің меншікті мəндерін жəне меншікті функцияларын табуға болады.

Толқындық теория бойынша жарықтың интенсивтігі берілген нүктедегі электр векторының амплитудасының квадратына пропорционал, ал корпускулалық теория бойынша бірлік беттен бірлік уақытта өткен фотондар санына (nф) пропорционал. Олай болса жарық векторының амплитудасының квадраты бірлік беттен бірлік уақытта өткен фотон санына пропорционал немесе осы беттен өту ықтималдығына пропорционал деп санауға болады.

Осылайша қарастыру электронға қолданылса, толқындық функцияның физикалық мағынасы: қарастырылып отырған көлем

элементі - dV болса, онда ₀ ² dV - толқындық функцияның амплитудасымен көлем элементінің көбейтіндісі, электроның көлем элементінде болу ықтималдығын көрсетеді. Сонда электронның алынған көлем элементінде болу ықтималдылығы толқындық функцияның амплитудасының квадраты жəне көлем элементіне пропорционал болады.

2. Шредингер теңдеуін шешу мысалдары

Шредингер теңдеуі, толқындық теңдеу - релятивистік емес кванттық механиканың негізгі теңдеуі. Мұны алғаш рет Э. Шредингер тапты (1926) . Ньютонның механикадағы қозғалыс теңдеулері мен Максвелл электрдинамикадағы теңдеулері классик. физикада қандай түбегейлі рөл атқарса, Шредингер теңдеуі кванттық механикада сондай рөл атқарады. Шредингер теңдеуі толқындық функция (пси функция) арқылы кванттық нысандар күйінің уақыт бойынша өзгеруін сипаттайды. Егер бастапқы кездегі толқындық функцияның мәні 0 белгілі болса, онда Шредингер теңдеуін шешу арқылы осы функцияның кез келген уақыт мезетіндегі мәнін (x, y, z, t) табуға болады. V(x, y, z, t) потенциалы тудыратын күштің әсерінен қозғалатын, массасы m бөлшек үшін Шредингер т. мына түрде жазылады:, мұндағы d2/dx2+d2/dy2+d2/dz2 Лаплас операторы, =h/2 - Планк тұрақтысы. Бұл теңдеу Шредингердің уақытқа тәуелді теңдеуі деп аталады. Егер V уақытқа тәуелсіз болса, онда Шредингер теңдеуі төмендегі түрде жазылады:, мұндағы Е-кванттық жүйенің толық энергиясы. Бұл теңдеу Шредингердің стационер күйдегі теңдеуі деп аталады. Кеңістіктің шектелген аумағында қозғалатын кванттық жүйелер (бөлшектер) үлесі Шредингер теңдеуінің шешімі энергияның кейбір дискретті (үздікті) мәндерінде n1, n2, …, nn, … ғана болады; бұл қатардың мүшелері бүтін кванттық сандармен (n) нөмірленеді. Әрбір n-нің мәніне n (x, y, z) толқындық функциясы сәйкес келеді. Толқындық функцияның толық жиынтығы n1, n2, …, n, белгілі болса, кванттық жүйенің барлық параметрлерін анықтауға болады. Шредингер теңдеуі табиғаттағы микробөлшектердің бөлшектік-толқындық қасиеттерін матем. өрнек арқылы толық сипаттайды және ол сәйкестік принциптерін қанағаттандырады. Бұл теңдеу шекті жағдайда (де Бройль толқынының ұзындығы қарастырылып отырған қозғалыстың өлшемдерінен әжептәуір кіші болғанда) бөлшектердің қозғалысын классик. механика заңдарымен сипаттауға мүмкіндік береді. Шредингер теңдеуінен қозғалысты траектория арқылы сипаттайтын классик. механика теңдеулеріне ауысу толқындық оптикадан геометрик. оптикаға ауысуға ұқсас. Матем. көзқарас бойынша Шредингер теңдеуі толқындық теңдеуге жатады және өзінің құрылымы бойынша периодты әсер ететін жіңішке ішектің тербелісін сипаттайтын теңдеуге ұқсас. Бірақ ішектің тербелісін сипаттайтын теңдеудің шешімі берілген уақыт мерзіміндегі ішектің геометр. пішінін беретін болса, ал Шредингер теңдеуі шешімінің тікелей физикалық мағынасы болмайды. Дегенмен толқындық функция квадратының n(x, y, z, t) /2 физикалық мағынасы бар. Ол бөлшектің температурасы ӘС уақыт мезетіндегі координаттары x, y, z, нүктенің төңірегінде бірлік көлемде болу ықтималдылығын анықтайды. Ықтималдықтарды қосу теоремасына сүйеніп микробөлшекті температурасы ӘС уақыт кезеңінде шекті V көлемде мына өрнек арқылы табуға болады: мұндағы W - микробөлшектің V көлемде орналасу ықтималдылығы. Бірөлшемді шексіз терең потенциалдық шұңқырдағы микробөлшектің күйі.

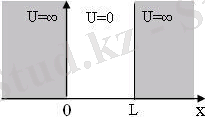
Массасы m бөлшек Ох осі бойымен ғана қозғалсын. Бөлшектің қозғалысы шұңқырдың қабырғаларымен шектеулі, қабырғалардың координаталары x=0 және x=L. Мұндай өрістегі бөлшектің потенциалдық энергиясы 11. 1 - суретте көрсетілген. Бөлшектің 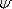функциясы х координатасына ғана тәуелді болғандықтан, Шредингердің (11. 4) стационарлық теңдеуі мына түрде жазылады

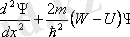(11. 5)

Бөлшек шұңқырдан шыға алмайды, сондықтан 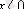және 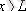аймақтарда 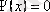. Пси-функцияның үздіксіздік шартынан шығатыны, шұңқырдың шекараларында ол нөлге тең болуы қажет

11. 1 сурет

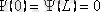. (11. 6)

Шекаралық шарт - (11. 6) теңдеуі (11. 5) теңдеуіне қосымша. Шұңқырдың шектерінде (бұл аймақта 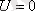) (11. 5) өрнегі мына түрде жазылады

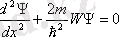. (11. 7)

Бұл теңдудің шешімін табу дегеніміз, бөлшектің 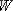(знергетикалық спектр) толық энергиясының мүмкін мәндерін және осы мәндерге сәйкес келетін 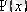толқындық функциясын табу.

Жоғарыдағы (11. 7) теңдеуі - тербелістер теориясындағы белгілі теңдеу. Ол (11. 6) шартты энергияның мына мәндерінде қанағаттандырады

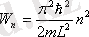, (11. 8)

мұндағы 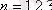- бүтін сандар.

Бұл нәтиже микробөлшектің потенциалдық шұңқырдағы энергетикалық спектрі дискретті және бөлшек энергиясы квантталатынын көрсетеді. Ал 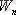энергияның кванттық мәндері - энергия деңгейлері , n - бас кванттық сан деп аталады.

Бөлшектің меншікті функциясы (11. 8) өрнегіне сәйкес,

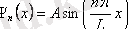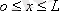, . (11. 9)

Нормалау (11. 2) шартынан 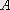коэффициенті табылады,

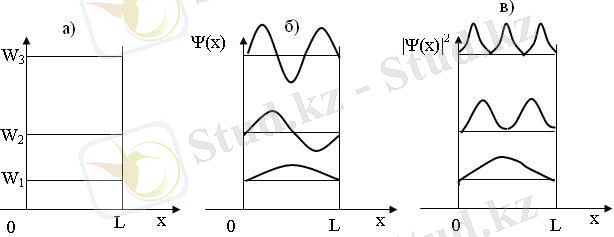
11. 2 сурет

және (11. 9) өрнегі мына түрде жазылады

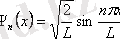. (11. 10)

Бөлшектің потенциалдық шұңқырдағы энергетикалық деңгейлері 11. 2 -суретте (а), сонымен қатар 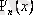функциясының сызбасы (б) және координатасы х нүкте айналасында бөлшектің болуының 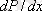(в) - ықтималдық тығыздығының сызбалары келтірілген.