Диофант теңдеулерінің теориясы мен шешу алгоритмдері: екі белгісізді және жоғары дәрежелі теңдеулер


Кіріспе
Математиканы оқытудың маңыздылығы математикалық ойлау стилінің қалыптасуы болып табылады. Математикалық білім беру жалпы адамның мәдени қалыптасуына үлес қосады.
Қазіргі кезде шешімі ылғи айқын болмаса да, адамның алдына көптеген міндеттер қойылуда. Сондықтан кейде бұл сұрақтардың дұрыс жауабы көптеген нұсқалармен берілуі мүмкін. Үйлесімді және дұрыс нұсқаны қалай таңдауға болады?
Міне, математиканың ең әдемі тарауларының бірі - бүтін сандардағы теңдеулерді шешу тақырыбы осы сұрақпен тығыз байланысты. Бұл ғылыми жоба бүтін санды теңдеулерге арналған сандар теориясының арифметикалық мағынасын қарастырады.
Анықталмаған теңдеулерді қазір диофант теңдеулері деп те атайды. Ол әрбір теңдеудің тек бір ғана рационал шешуін анықтаумен шектеледі. Онда анықталмаған теңдеулерді жалпы шешу тәсілдері жоқ. Шыққан нәтиженің дұрыстығы дәлелденбейді, тек есеп шартын қанағаттандыруы ғана тікелей тексеріледі.
Зерттеу жұмысының мақсаты
- олимпиадалық есептерде кездесетін теңдеулерді диофанттық теңдеулерді шешу алгоритімі бойынша қарастыру ;
- анықталмаған теңдеулерді шешудің әдіс-тәсілдерінің тиімділігін көрсету;
-жеке тұлғаның шығармашылық, ізденімпаздылық қабілетін дамыту;
-диофант теңдеулерінің теориясын және осы тақырыпқа арналған таңдамалы есептерді шығару жолдарын қарастыру
Зерттеу жұмысының міндеті
-Екі белгісізді екінші дәрежелі диофант теңдеулерін зерттеу
- Дәрежесі екіден жоғары екі белгісізді диофант теңдеулерін зерттеу
-таңдамалы есептерді шығара білу
Зерттеу жұмысының өзектілігі
Қазіргі таңдағы өзекті мәселелердің бірі математика пәні бойыша ҰБТ- да немесе олимпиадаларда кездесетін, бірақ мектеп бағдарламасында терең игерілмеген күрделі есептерді шешудің әдіс - тәсілдерін қолдана білу.
Осындай күрделі есептердің біріне диофант теңдеулерін жатқызуға болады.
Менің зерттеу жұмысымның өзектілігі - осы әдіс - тәсілдерді диофант теңдеулеріне қолдана отырып, есептер құрастыру және теңдеулерді оңай жолмен шешу.
Зерттеу жұмысының болжамы
Егер диофант теңдеулерді бүтін сандар жиынында шешудің әдемі әрі тиімді тәсілдерін терең зерттеп, қарастыратын болсақ:
- Дәрежесі екіден жоғары екі айнымалысы бар теңдеулердің нақты шешімін табуға болады.
Зерттеу жұмысының жаңашылдығы
Диофант теңдеулерді бүтін сандар жиынында шешудің әдемі әрі тиімді тәсілдерін терең зерттеп, қарастыра келе, дәрежесі екіден жоғары екі айнымалысы бар теңдеулердің нақты шешу жолдары анықталды.
І. Диофант теңдеулері
1. 1 Бір белгісізді Диофант теңдеулері
Бір белгісізді бірінші дәрежелі теңдеуді қарастырайық.
a 1 x + a 0 = 0 (1. 1)
мұндағы a 1 және a 0 - бүтін сандар. Егер де a 0 саны a 1 - ге бөлінсе, онда
бұл теңдеу бүтін сан болады:
 .
.
Бүтін сандарда (1) теңдеудің әрқашан шешімі бола бермейді. Осы екі теңдеудің, мысалы: 3x - 27 = 0 және 5x + 21 = 0 . Бірінші теңдеудің шешімі бүтін сан болса, ал екінші теңдеудің шешімі жоқ.
Дәрежесі бірден үлкен болғанда теңдеулер оқиғасында да мұндай жағдайды кездестіруге болады:
Мысалы, бірінші теңдеудің
x
2
+ x - 2 = 0, x
1
= 1, x
2
= -2 -
бүтін шешімі бар, ал мына жағдайда бүтін санның шешімі болмайды, себебі оның түбірі иррационал
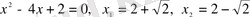 .
.
Бүтін коэффициентті n - дәрежелі бүтін түбірлі теңдеу мына формуламен жеңіл табылады.
a n x n + a n -1 x n -1 + . . . + a 1 x + a 0 = 0 ( n ≥ 1) (1. 2)
нақты x = a мына теңдеудің бүтін түбірі болса, онда
a 0 = - a ( a n a n - 1 + a n - 1 a n - 2 + . . . + a 1 )
Соңғы теңдеуден
 -
дің
-
дің
 -
ға қалдықсыз бөлінетіні көрініп тұр; қарастыра келе, әр бүтін түбірі бар
(2) -
теңдеу бос теңдеулер жиынының бөліндісі болып келеді. Теңдеудегі бүтін сандардың шешімін табу үшін, бөлінділерден
-
ға қалдықсыз бөлінетіні көрініп тұр; қарастыра келе, әр бүтін түбірі бар
(2) -
теңдеу бос теңдеулер жиынының бөліндісі болып келеді. Теңдеудегі бүтін сандардың шешімін табу үшін, бөлінділерден
 -
ді табу керек, оны теңдеуге қойған кезде тепе
-
теңдікке айналдырады. Мысалы,
1, -1, 2
және
-2
сандарының барлық бөлінділері өзара бос мүше теңдеуін көрсетеді
x
10
+ x
7
+ 2x
3
+ 2 = 0,
мұнда тек қана бір түбір болады, яғни
x = -1
. Осы әдіс арқылы мына теңдеудің
x
6
- x
5
+ 3x
4
+ x
2
- x + 3 = 0
бүтін сандарда шешімі болмайтынын жеңіл дәлелдеуге болады. [1]
-
ді табу керек, оны теңдеуге қойған кезде тепе
-
теңдікке айналдырады. Мысалы,
1, -1, 2
және
-2
сандарының барлық бөлінділері өзара бос мүше теңдеуін көрсетеді
x
10
+ x
7
+ 2x
3
+ 2 = 0,
мұнда тек қана бір түбір болады, яғни
x = -1
. Осы әдіс арқылы мына теңдеудің
x
6
- x
5
+ 3x
4
+ x
2
- x + 3 = 0
бүтін сандарда шешімі болмайтынын жеңіл дәлелдеуге болады. [1]
1. 2 Екі белгісізді бірінші дәрежелі теңдеулер
Екі белгісізді бірінші дәрежелі теңдеуді қарастырайық.
ax + by + c = 0 (2. 1)
мұндағы а және b - нөлден өзгеше бүтін сандар, ал с - кез келген бүтін сан. Яғни, ең үлкен ортақ d = (a, b) бөлгіші 1 - ден артық болса, онда мына теңдіктер орындалады: a = a 1 d, b = b 1 d; (3) теңдеу мына түрге келеді:
(a 1 x + b 1 y) d + c = 0.
Егер
с
саны
d -
ға бөлінсе, онда осы теңдеудің шешімі болады. Осыдан,
 болса, онда барлық коэффициенттер
d -
ға бөлінеді де,
(3)
теңдеуді
d -
ға қысқартып, мынадай теңдеу аламыз:
болса, онда барлық коэффициенттер
d -
ға бөлінеді де,
(3)
теңдеуді
d -
ға қысқартып, мынадай теңдеу аламыз:
a
1
x
+
b
1
y
+
c
1
= 0,
 .
.
 және
және
 коэффициенттері үшін
с
= 0 жағдайын қарастырайық. Онда
(3)
теңдеу былай жазылады:
коэффициенттері үшін
с
= 0 жағдайын қарастырайық. Онда
(3)
теңдеу былай жазылады:
ax + by = 0 (2. 1')
х - ке қатысты осы теңдеуді шешкенде, мынаны аламыз:
 .
.
Егер у саны а - ға қалдықсыз бөлінсе, онда х - тің мәні бүтін сан болады. Бірақ у - ті а арқылы былай жазуға болады:
y = at ,
мұндағы
t
(
t
= 0,
 . Осы белгілеуді келесі теңдеуге қойса:
. Осы белгілеуді келесі теңдеуге қойса:
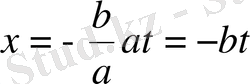 ,
,
келесі формуланы аламыз:

Келесі жағдайға көшейік. Егер
 болса.
болса.
Алдымен (3) теңдеудің нақты шешімдерін тауып, яғни x 0 , y 0 - ді:
ax 0 + by 0 + c = 0.
Теорема 1 . a және b сандары жай сандар болсын және (3) - теңдеудің шешімі [ x 0 , y 0 ] болсын. Онда осы формулалар (3) теңдеудің шешімдері
x = x 0 - bt, y = y 0 + at (2. 2)
формуласымен беріледі. [2. 65] .
Дәлелдеу . [x 0 , y 0 ] - (3) теңдеудің кез келген шешімі болсын. Осы теңдіктерден ax + by + c = 0 және ax 0 + by 0 + c = 0 екені шығады. Осыдан:
ax - ax
0
+ by - by
0
= 0;
 .
.
y - y 0 - бүтін сандар және a, b - өзара жай сандар. Сондықтан x 0 - x саны b - ға қалдықсыз бөліну керек, яғни x 0 - x мынадай түрге келеді:
x 0 - x = bt ,
мұндағы t - бүтін сан. Онда
 ,
,
және x = x 0 - bt, y = y 0 + at деп аламыз.
(4) теңдеудің түрі мынадай болады: [x, y], [x 1 , y 1 ] (4) формула бойынша
t = t 1, (3) теңдеудің шешімі болады. Осындай тексеру жүргізу үшін x = x 0 - bt,
y = y 0 + at (3) теңдеудің сол жағына қояйық.
ax 1 + by 1 + c = ax 0 - abt 1 +by 0 +abt 1 + c = ax 0 + by 0 +c , бірақ [ x 0 , y 0 ] - шешімі, онда
ax 0 + by 0 +c = 0, ax 1 + by 1 + c = 0,
яғни [x 1 , y 1 ] - (3) теңдеудің шешімі. Осымен теорема дәлелденді.
Сонымен, ax + by + c = 0 теңдеуінің бір ғана шешімі белгілі болса, онда қалған шешімдері арифметикалық прогрессиядан табылады:
x 0 - x = bt , y = y 0 + at.
Ескере кетейік, с = 0 болғанда, x = -bt, y = at формуланың шешімдері мына формуладан белгілі болады:
x 0 - x = bt , y = y 0 + at.
Егер x 0 = y 0 = 0 болса, онда x = 0, y = 0 мынау теңдеудің шешімі болады:
ax + by = 0
Егер
 болса, онда (3) теңдеудің
болса, онда (3) теңдеудің
 бола ма? Мысал келтірейік.
бола ма? Мысал келтірейік.
 - теңдеуі берілсін.
- теңдеуі берілсін.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,

Ақырғы шешімге келеміз:
 ,
,


 .
.
Осы теңдеудің шешімі х = 9, у = 22 болады. Және теорема бойынша оның барлық шешімі прогрессия арқылы табылады:


 қысқартылмайтын бөлшегін қарастырайық.
a
-ның
b
-ға бөлгендегі
қысқартылмайтын бөлшегін қарастырайық.
a
-ның
b
-ға бөлгендегі

және қалдығын
 деп белгілейік. Онда мынаны аламыз:
деп белгілейік. Онда мынаны аламыз:
 .
.
Енді
b
-ны
 -ге бөлгендегі
-ге бөлгендегі
 - және
- және
 - қалдығы болсын. Онда
- қалдығы болсын. Онда

Дәл солай

 , (2. 3)
, (2. 3)
 (2. 4)
(2. 4)
Алынған теңдеуді мынадай түрге келтірейік:



Дәл сол сияқты
 және т. с.
және т. с.

 -ны
k
түрінде жазайық.
-ны
k
түрінде жазайық.


Осыдан мынаны аламыз:
P 3 = P 2 q 3 + P 1 ; Q 3 = Q 2 q 3 + Q 1 .
Индукцияны қолданып, осы қатынасты сол сияқты екені көрініп тұр
P k = P k-1 q k + P k-2 , Q k = Q k-1 q k + Q k-2 (2. 5)
барлық
 үшін орындалады.
үшін орындалады.

 -
ның орнына
-
ның орнына
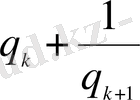 -
ді қойсақ:
-
ді қойсақ:

Осыдан,
 болғандықтан,
болғандықтан,


Осылай,
 үшін (7) теңдеу
үшін (7) теңдеу
 үшін де орындалады.
үшін де орындалады.
Енді,

 (2. 6)
(2. 6)
Әрине,

(7) формуланы қолдана отырып,

Жақша ішіндегі өрнек, k -ны k - 1-мен алмастыру арқылы шығады. Осылай алмастыруды жалғастыра отырып, мынадай теңдеу аламыз:

Осыдан,

(8) теңдеуді қолдана отырып, егер k = n болса:
 (2. 7)
(2. 7)
Енді теңсіздікті шешуге келейік.
ax + by + c = 0, (a, b) = 1 . (2. 8)
(9) қатынасты былай жазайық:


(-1) n - 1 c - ке көбейтейік. Онда
a[(-1) n - 1 cQ n - 1 ] + b[(-1) n cP n - 1 ] + c = 0.
Осыдан, [x 0 , y 0 ] сандары үшін
 (2. 9)
(2. 9)
(10) теңдеудің шешімдері болады да, теорема бойынша осы барлық теңдеулердің шешімдері мынадай болады:

1. 3 Екі белгісізді екінші дәрежелі теңдеулер
Көп жағдайда екі белгісізді екінші дәрежелі теңдеуде х және у бүтін сандарында аз жағдайда шекті санға ие болады. Мына теңдеуді қарастырсақ:
a 0 x n + a 1 x n - 1 y + a 2 x n - 2 y 2 + … + a n y n = c
мұнда n - бүтін сан, яғни екіден жоғары, ал a 0 , a 1 , a 2 , …, a n , c - бүтін сандар.
Біздің ғасырымыздың басында А. Туэнің дәлелдеуі бойынша, мұндай теңдеу бірыңғай бірінші дәрежелі екімүше және екінші дәрежелі үшмүше сол жақтағы бірыңғай бөлімнің теңдеуі болып келген жағдайда х және у бүтін сандарының шешімі шекті болады. Осы ақырғы оқиғада біздің теңдеу екі формуланың біреуін қабылдайды.
(ax + by) n = c 0 , (ax 2 + bxy + cy 2 ) n = c 0 , (3. 1)
сонымен, бірінші және екінші дәрежелі теңдеуге қосылады, бұл шешімде
 -
ге тең болуы үшін,
n -
ші дәрежелі бүтін сан болуы керек. Бұл жерде А. Туэнің әдісін қолдана алмаймыз, себебі кейбір түсініктемелерде теңдеу шешімінің шекті санының тапсырмасын дәлелдеу күрделі болуына байланысты.
-
ге тең болуы үшін,
n -
ші дәрежелі бүтін сан болуы керек. Бұл жерде А. Туэнің әдісін қолдана алмаймыз, себебі кейбір түсініктемелерде теңдеу шешімінің шекті санының тапсырмасын дәлелдеу күрделі болуына байланысты.
(1) теңдеудің екі бөлімін y n бөлейік. Сонда біздің теңдеуіміз мына түрді қабылдайды:
 (3. 2)
(3. 2)
бұл теңдеу жеңіл болуы үшін:
 (3. 3)
(3. 3)
біздің жорамалымыз бойынша барлық түбір әр түрлі және
 , бірақ бұл теңдеудің түбірі төменгі дәрежелі бүтін коэффициентті бола алмайды. Бұл оқиға біздің сұрағымыздың негізі болып келеді. [4]
, бірақ бұл теңдеудің түбірі төменгі дәрежелі бүтін коэффициентті бола алмайды. Бұл оқиға біздің сұрағымыздың негізі болып келеді. [4]
Жоғары алгебраны дәлелдеуде, алгебралық теңдеудің кем дегенде бір түбірі болады, осыдан кез келген көпмүше z - a бүтінге бөлінеді, егер a - оның
түбірі болса, осыдан көпмүшені туынды түрде көрсету
 (3. 4)
(3. 4)
мұнда a 1 , a 2 , …, a n - барлық берілген көпмүшелердің n түбірі болады. Осы көпмүшені туынды түрінде қолдана отырып, біз (2) теңдеуді мына түрде көшіріп аламыз.
 (3. 5)
(3. 5)
Айталық,
(4)
теңдеуде
[x
k
; y
k
]
бүтін сандарында шексіз көп шешім болады. Яғни,
у
абсолюттік ұзындығында қандай да бір шешім болады. Егер шексіз көп жұп шектеулі болса, қандай да бір анық сан абсолюттік ұзындық бойынша аз,
у
қандай да,
х -
тан үлкен, онда мұндай жағдайда
х -
тың сол жақ бөлігі үлкен болар еді, ал оң жақ бөлігі шектеулі күйінде қалар еді, бұл мүмкін емес.
у
үлкен болсын делік, онда (4) теңдеудің оң жақ бөлігі кем болады, яғни, сол жақ бөлігі де кем болуы керек. Бірақ теңдеудің сол жақ бөлігінде
 және
және
 құрайтын
n
көбейтінді туындысы бүтін болғанда бірден кем болмайды. Яғни, сол жақ бөлігінің кем болуы, абсолюттік ұзындықтың қандай да бір түріне сәйкес келеді.
құрайтын
n
көбейтінді туындысы бүтін болғанда бірден кем болмайды. Яғни, сол жақ бөлігінің кем болуы, абсолюттік ұзындықтың қандай да бір түріне сәйкес келеді.
 .
.
Бұл айырмашылық тек мына жағдайда кем болуы мүмкін, егер
 шынымен теңсіздік орны болмаса
шынымен теңсіздік орны болмаса
 . Ал басқа жағдайда біздің айырмашылығымыздың модулі кем болуы мүмкін емес, себебі
. Ал басқа жағдайда біздің айырмашылығымыздың модулі кем болуы мүмкін емес, себебі
 .
.
Теңдеудің сол жақ бөлігінің екі айырмашылығы, екі көбейткіші бір уақытта модуль бойынша кем бола алмайды, себебі
 (3. 6)
(3. 6)
күшіне қарай, сандар арасында
 біркелкілері жоқ. Егер бір айырмашылық модуль бойынша кіші болса, немесе абсолюттік ұзындығы
біркелкілері жоқ. Егер бір айырмашылық модуль бойынша кіші болса, немесе абсолюттік ұзындығы
 . Бұл абсолюттік ұзындықтың мәні абсолюттік ұзындықтың мәнінің нәтижесінен аспайды. Яғни барлық сандардай
. Бұл абсолюттік ұзындықтың мәні абсолюттік ұзындықтың мәнінің нәтижесінен аспайды. Яғни барлық сандардай
 өзара әр түрлі болса, онда абсолюттік ұзындықтың мәні ең кіші немесе модуль айырмашылығы
өзара әр түрлі болса, онда абсолюттік ұзындықтың мәні ең кіші немесе модуль айырмашылығы
 нөлден жоғары болады (m ≠ s) . Ұзындықты 2
d
арқылы белгілеп,
у
-тың шексіз өсуіне байланысты қандай да бір
у
-тың үлкен болуы жеткілікті.
нөлден жоғары болады (m ≠ s) . Ұзындықты 2
d
арқылы белгілеп,
у
-тың шексіз өсуіне байланысты қандай да бір
у
-тың үлкен болуы жеткілікті.
 ,
,
яғни
 (3. 7)
(3. 7)
Онда абсолюттік ұзындық немесе модуль, абсолюттік ұзындықтың туындысы туындыға, модульға немесе көбейтінділерге тең болса, онда (4) теңдеуден мына теңдеуді аламыз:
 (3. 8)
(3. 8)
Бірақ бұл теңдікте айырмашылықтың әрқайсысын
 кішкентай ұзындығына ауыстырсақ, ал
кішкентай ұзындығына ауыстырсақ, ал
 -
ді бірлікке ауыстырсақ, ондағы
-
ді бірлікке ауыстырсақ, ондағы
 бүтін саннан кем бола алмайды, онда
(7)
теңдеудің сол жақ бөлігі оң жақ бөлігінен кіші болады және біз мына теңсіздікті аламыз:
бүтін саннан кем бола алмайды, онда
(7)
теңдеудің сол жақ бөлігі оң жақ бөлігінен кіші болады және біз мына теңсіздікті аламыз:

немесе
 , (3. 9)
, (3. 9)
мұндағы
c
1
, x
n
мен
 -
нен тәуелсіз.
-
нен тәуелсіз.
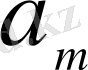 саны
n -
нен аса көп емес, ал
[x
k
; y
k
]
жұптары, қандай да бір
(8)
теңсіздігінде
m
болуы қажет. Сонда анық
m
саны болады, және
(8)
теңсіздікте
a
m
шексіз көп қолданылады. Басқа сөзбен айтқанда,
(1)
теңдеудің бүтін сандарда шексіз көп шешім болады, яғни
(3)
бүтін коэффициентті алгебралық теңдеуінде
а
түбірі болады, сонда қандай да бір
q
үлкен болса теңсіздік орындалады. [5] .
саны
n -
нен аса көп емес, ал
[x
k
; y
k
]
жұптары, қандай да бір
(8)
теңсіздігінде
m
болуы қажет. Сонда анық
m
саны болады, және
(8)
теңсіздікте
a
m
шексіз көп қолданылады. Басқа сөзбен айтқанда,
(1)
теңдеудің бүтін сандарда шексіз көп шешім болады, яғни
(3)
бүтін коэффициентті алгебралық теңдеуінде
а
түбірі болады, сонда қандай да бір
q
үлкен болса теңсіздік орындалады. [5] .
 , (3. 10)
, (3. 10)
мұндағы А - тұрақты, p және q сандарына тиісті емес. p және q - бүтін сандар, ал n - дәрежелі теңдеу, бұл а - ны қанағаттандырады. Егер а нақты санның туындысы болса, онда оны былай таңдауға болады. p және q бүтін сандарының (9) теңсіздікте нақты шексіз көп шешімі болады. Бірақ біздің оқиғада бүтін коэффициентті алгебралық теңдеудің а түбірі болып келеді. Мұндай сандар алгебралық теңдеу деп аталады және негізгі құрылымға ие болады. Алгебралық санның дәрежесі деп бүтін коэффициентті алгебралық теңдеудің ең кіші дәрежедегі дәрежені айтамыз және ол бұл санды қанағаттандыруы керек.
А. Туэнің дәлелдеуі бойынша, p және q бүтін санында алгебралық санның а - дәрежедегі n теңсіздіктің шешімі тек шексіз сан болады. [6] .
 (3. 11)
(3. 11)
Бірақ егер
 (9)
теңсіздіктің оң жақ бөлігі
(10)
теңсіздіктің оң жақ бөлігінен
q
кіші болады, себебі
(9)
теңсіздіктің оң жақ бөлігі
(10)
теңсіздіктің оң жақ бөлігінен
q
кіші болады, себебі
 . Осыған орай
(10)
теңсіздігі
p
және
q
бүтін сандарында шекті сан шешімін қабылдай алады, яғни
(9)
теңсіздік те тек шекті сан шешімін қабылдайды.
n = 2
кез келген
А -
ға байланысты болғанда
(1)
теңдеу бүтін сандар шекті сан шешімін қабылдайды, егер
(3)
теңдеудің барлық түбірі бүтін коэффициентті теңдеудің
n -
ге қарағанда дәреженің түбірі болса,
p
және
q
бүтінінің шексіз көп шешімі болатынын жеңіл құрастыруға болады. Осыған байланысты А. Туэнің теоремасы әрі қарай күрделене түсті. Осыған орай А. Туэнің дәлелдеу әдіс теоремасының принципі ұзындыққа арналған жоғары шегінің шешімін табуға мүмкіндік бермейді, басқа сөзбен айтқанда,
. Осыған орай
(10)
теңсіздігі
p
және
q
бүтін сандарында шекті сан шешімін қабылдай алады, яғни
(9)
теңсіздік те тек шекті сан шешімін қабылдайды.
n = 2
кез келген
А -
ға байланысты болғанда
(1)
теңдеу бүтін сандар шекті сан шешімін қабылдайды, егер
(3)
теңдеудің барлық түбірі бүтін коэффициентті теңдеудің
n -
ге қарағанда дәреженің түбірі болса,
p
және
q
бүтінінің шексіз көп шешімі болатынын жеңіл құрастыруға болады. Осыған байланысты А. Туэнің теоремасы әрі қарай күрделене түсті. Осыған орай А. Туэнің дәлелдеу әдіс теоремасының принципі ұзындыққа арналған жоғары шегінің шешімін табуға мүмкіндік бермейді, басқа сөзбен айтқанда,

 және
және
 мүмкін ұзындық шегінің
мүмкін ұзындық шегінің
 ,
a
1
, a
2
, …, a
n
және
с
коэффициенттері бойынша. Бұл сұрақ қазіргі күнде, яғни ұзындық шешімінің шегін табуға мүмкіндік жоқ екені ашық айтылады. Бірақ А. Туэнің әдісі арқылы
(3)
теңдеудің шегі бар сандар шешімін табуға болады, бірақ ол өте күрделі болып келеді. Бұл теңдеу түрі арнайы сыныптарға тереңдетіп түсіндірілген.
,
a
1
, a
2
, …, a
n
және
с
коэффициенттері бойынша. Бұл сұрақ қазіргі күнде, яғни ұзындық шешімінің шегін табуға мүмкіндік жоқ екені ашық айтылады. Бірақ А. Туэнің әдісі арқылы
(3)
теңдеудің шегі бар сандар шешімін табуға болады, бірақ ол өте күрделі болып келеді. Бұл теңдеу түрі арнайы сыныптарға тереңдетіп түсіндірілген.
Мысалы, математик Б. Н. Делон көрсеткендей, мына теңдеу бойынша
ax 3 + y 3 = 1.
а бүтіні х және у бүтін сандарында x = 0, y = 1 - ден басқа, тек қана бір шешімі болады. Бұдан басқа, мына теңдеуде
ax 3 + bx 2 y + cxy 2 + dy 3 = 1 .
a , b , c және d бүтіндері х және бүтінінде бес шешімі болады.
P (x, y) бүтін коэффициентті х және у - ке қатысты көпмүше болсын, яғни
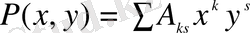 ,
,
мұндағы A ks - бүтін сан. Егерде бүтін коэффициентті басқа екі көпмүшемен туынды ретінде көрсету мүмкін болмаса, біз оны келтірілмейтін көпмүше деп атаймыз, және оның әрқайсысы жай сан. К. Зигель өте күрделі және негізгі әдіс бойынша мына теңдеуді:
P (x, y) = 0,
былай дәлелдеді.
P (x, y) - келтірілмейтін көпмүше екінші дәрежелі x , y - ке қарағанда жоғары болады. х және у бүтінінде шексіз көп шешімі болады, егер a n , a n - 1 , …, a 0 , a -1 , …, a -n және b n, b n - 1 , …, b 0 , b -1 , …, b -n бүтін болса, біздің теңдеуге x, y орнына мынаны қойсақ:

біз тепе-теңдікті аламыз
P (x, y) = 0
мұндағы n - кез келген бүтін сан.
1. 4 Дәрежесі екіден жоғары екі белгісізді теңдеулер
Кейбір ерекше жағдайлардан басқа дәрежесі екіден артық теңдеудің шешімдерінің саны ақырлы болады, егер x пен y бүтін сан болса. Ең алдымен біріншіден мына теңдеуді қарастырайық:
a 0 x n + a 1 x n - 1 y + a 2 x n - 2 y 2 + … + a n x n = c
мұндағы n - бүтін сан, екіден үлкен, және бүкіл сандар a 0 , a 1 , a 2, . . . , a n c - бүтін сандар.
Ғасыр басында А. Туэ дәлелдеген, мұндай теңдеу санның соңғысы есептеудің бүтін сандары x және y тек қана осындай жағдайларда болады, теңдеудің сол жағы бір текті бөлігі бірінші дәрежелі екі мүше немесе екінші дәрежелі үш мүше болғанда, осы жағдайда теңдеу мынадай түрде болады:

 ,
,
Біз мұндай жағдайда А. Туэ әдісін дәлелдеуі бойынша соңғы санның теңдеуін шығады. Теңдеудің екі жағын бөліп шығарамыз, сонда теңдеуіміз осындай түрге келеді:
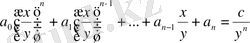
Қарапайым болу үшін теңдеүдің түбірі:

 , бұл теңдеудің түбірі бола алмайды.
, бұл теңдеудің түбірі бола алмайды.
Жоғары алгебрада дәлелденеді, әр түрлі алгебра теңдеулерде болмаса да бір түбірі болады, бұдан шығатыны көп мүше бөлінеді z - a , егер a оның түбірі,
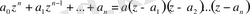
мұндаға

 . . . ,
. . . ,
 көпмүшенің түбірі. Осыдан мынадай формула шығады:
көпмүшенің түбірі. Осыдан мынадай формула шығады:

Теңдеудің бүтін сандар арасында
 шешімдер саны ақырсыз болсын. Онда,
y
k
абсолюттік шамасы шектелмейді. Онда,
x
k
абсолюттік шамасы шектелмейтін болады. Онда теңдеудің сол жағы шектелмейтін, ал оң жағы шектелген болады. Бұл мүмкін емес. Енді
y
k
абсолют шамасы өте үлкен болсын, онда теңдеудің оң жағы кішкентай болуы керек. Бірақ теңдеудің сол жағы
шешімдер саны ақырсыз болсын. Онда,
y
k
абсолюттік шамасы шектелмейді. Онда,
x
k
абсолюттік шамасы шектелмейтін болады. Онда теңдеудің сол жағы шектелмейтін, ал оң жағы шектелген болады. Бұл мүмкін емес. Енді
y
k
абсолют шамасы өте үлкен болсын, онда теңдеудің оң жағы кішкентай болуы керек. Бірақ теңдеудің сол жағы
 және
a
0
көбейтіндісі болады. Ал
және
a
0
көбейтіндісі болады. Ал
 абсолют шамасы бойынша бірден кем емес. Осы айырым
a
m
нақты сан болғанда кішкентай болады, яғни
a
m
=a+bi,
абсолют шамасы бойынша бірден кем емес. Осы айырым
a
m
нақты сан болғанда кішкентай болады, яғни
a
m
=a+bi,
 теңдігі орындалмайды. Қарсы жағдайда айырымның модулі мейлімше кішкентай болады. Өйткені
теңдігі орындалмайды. Қарсы жағдайда айырымның модулі мейлімше кішкентай болады. Өйткені

Сол жақтағы көбейтіндінің екі көбейткіші бір мезгілде абсолюті кішкентай бола алмайды, өйткені формула және a m әр түрлі.

Егер айырымның абсолют шамасы
 кем болса, онда екіншісі теңдік бойынша осы модульден кіші болуы керек. Бұл қосындының абсолют шамасы қосылғыштардың абсолют шамасынан аспайтыны шығады.
кем болса, онда екіншісі теңдік бойынша осы модульден кіші болуы керек. Бұл қосындының абсолют шамасы қосылғыштардың абсолют шамасынан аспайтыны шығады.
a
m
қос -қостан әр түрлі болғандықтан
 айырымның ең кіші мәні (
айырымның ең кіші мәні (
 ) оны
2d
деп белгілесек онда
y
k
меншікті үлкен мәніне
) оны
2d
деп белгілесек онда
y
k
меншікті үлкен мәніне
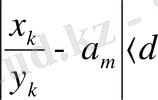
онда,
 s=1, 2, . . . , n,
s=1, 2, . . . , n,

Көбейтінің модулі көбейткіштердің модуліне тең болғандықтан

шығады . Осы теңдікте
 абсолют шамасын одан кіші d мәнімен, ал
абсолют шамасын одан кіші d мәнімен, ал
 мәнімен ауыстырса, онда теңдіктің сол жағы оң жағынан кіші болады
мәнімен ауыстырса, онда теңдіктің сол жағы оң жағынан кіші болады

және теңсіздіктер орындалады:

мұндағы
c
,
x
n
,
y
n
тәуелсіз.
a
m
сандарының саны m
-
нен аспайды, ал
 жұптарының саны ақырсыз. Сондықтан кейбір
q
үшін оған сәйкес
a
m
теңсіздік ақырсыз орындалады. Басқа сөзбен айтқанда егер теңдеудің бүтін шешімдерінің саны ақырсыз болса, онда коэффиценттері бүтін сан болатын алгебралық теңдеудің
q
мейлінше үлкен мәндерде теңсіздік орындалатын
a
түбірі табылады. [7] .
жұптарының саны ақырсыз. Сондықтан кейбір
q
үшін оған сәйкес
a
m
теңсіздік ақырсыз орындалады. Басқа сөзбен айтқанда егер теңдеудің бүтін шешімдерінің саны ақырсыз болса, онда коэффиценттері бүтін сан болатын алгебралық теңдеудің
q
мейлінше үлкен мәндерде теңсіздік орындалатын
a
түбірі табылады. [7] .
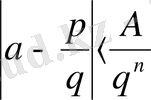
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz