Ренкин шартының мысалы

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 42 бет
Таңдаулыға:

ӘЛ-ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ

МЕХАНИКА-МАТЕМАТИКА ФАКУЛЬТЕТІ

АҚПАРАТТЫҚ ЖҮЙЕЛЕР КАФЕДРАСЫ

Бағдаршам туралы есеп
тақырыбына жазылған

ДИПЛОМДЫҚ ЖҰМЫС

Орындаған
______________________
(қолы)
Файзулла А.Т.
Ғылыми жетекші
ф.-м.ғ.д., профессор
_____________________
(қолы)
Кангужин Б.Е.

Норма бақылаушы
_____________________
(қолы)
Жуманов Ж.М.

Қорғауға жіберілді
Кафедра меңгерушісі
PhD докторы
_____________________
(қолы)
Бакибаев Т.И.

Алматы 2014

РЕФЕРАТ

Дипломдық жұмыс 49 беттен, 20 суреттерден, 15 қолданылған әдебиеттер мен 1 қосымшадан тұрады.
Кілт сөздер: БАҒДАРШАМ, МАКРОСКОПИЯЛЫҚ ҮЛГІ, МИКРО-СКОПИЯЛЫҚ ҮЛГІ, ТРАНСПОРТТЫҚ АҒЫМ, ТРАНСПОРТТЫҚ КЕП-ТЕЛІС, КЕПТЕЛІС ТЫҒЫЗДЫҒЫ, ЛАЙТХИЛЛ-УИЗЕМ-РИЧАРДС МОДЕЛІ.
Жұмыстың өзектілігі: Бүгінде жол жүрудің басты ережесі-бағдаршам. Онсыз қала көшелеріндегі кептелісте көлік жүргізуші мен қара жаяу халық үшін бір бағытта жүруге мүмкіндік жоқ. Сол себепті жолдың жөнделмеуі мен тұрғындар жиі жүретін көшелердегі бағдаршамдардың жетіспеуі күн тәртібінде күйіп тұрған мәселенің бірі болып тұр. Күресу жолдарының ең тиімді және арзан түрі транспорттық көлік ағымдарын математикалық пішіндеу арқылы зерттеу болып табылады.Сол себепті ҚР-да осы саланы дамыту өзекті мәселе деп есептеледі.
Жұмыстың зерттеу нысаны: Қалалық көлік қозғалыс ағындарының макроскопиялық және микроскопиялық үлгісі, ақпараттық жүйесі.
Жұмыстың мақсаты: Бағдаршам туралы есепті пайымдау.Кептеліс болдырмау.
Жұмыстың нәтижелері: Кинетикалық теңдеуден макроскопиялық модельдерді шығару.
Жұмыстың практикалық мағынасы: Әзірше дипломдық жұмыстың нәтижелері теоретикалық болып тұр, жұмыста аталған ұсыныстар өзге шет елдерде қолданыс тапқан. Практикада қолданылады деп болжанады.
Жұмыстағы қолданылған әдістер: Ықтималдықтар теориясының әдістері, пішіндеу әдістері, программалау әдістері.

РЕФЕРАТ

Дипломная работа состоит из 49 страниц, 20 рисунков, 15 источников и 1 приложения.
Ключевые слова: СВЕТОФОР, МАКРОСКОПИЧЕСКАЯ МОДЕЛЬ, МИКРОСКОПИЧЕСКАЯ МОДЕЛЬ, ТРАНСПОРТНЫЙ ПОТОК, ТРАНСПОРТНЫЙ ЗАТОР, ПЛОТНОСТЬ ЗАТОРА, МОДЕЛЬ ЛАЙТХИЛЛА-УИЗЕМА-РИЧАРДСА.
Актуальность работы: На сегодняшний день главным правилом дорожного движения является светофор. Без него в уличных заторах пешеход и водитель не могут двигаться в одном направлении. Есть множество различных способов борьбы против возникновения транспортных заторов.Самым выгодным и доступным способом борьбы является исследование транспортных потоков с помощью математического моделирования. Поэтому в РК развивать эту сферу является актуальной задачей.
Объект исследования: Макроскопическая и микроскопическая модель движения городского транспорта и информационные системы.
Цель работы: Основная цель: улучшить задачу светофора. Избежание заторов.
Результаты работы: Вывод макроскопических моделей из кинетического уравнения
Практическое значение работы: Пока что результаты работы являются теоретическими, приведенные предложения по улучшению дорожных движений используются в развитых странах. В дальнейшем планируется использование на практике
Использованные методы в работе: Методы теории вероятностей, методы моделирования, методы программирования.

ABSTRACT

Diploma project consists of 49 pages, 20 figures, 15 references and 1 appendix.
Keywords: TRAFFIC LIGHT, MACROSCOPIC AND MICROSCOPIC MO-DEL, TRAFFIC FLOW, CONGESTION, DENSITY CONGESTION, LWR'S MODEL.
Actuality: To date, the main rule is the traffic lights. Without him in the street congestion of pedestrians and drivers can not move in the same direction. There are many different ways to fight against the occurrence of congestion. The most profitable and affordable way to fight is to study the traffic flow using mathematical modeling. Therefore, in the Republic of Kazakhstan to develop this sphere is an urgent task.
Object of research: Macroscopic and microscopic model of urban transport and informatione systems.
Objective: The main objective: improve traffic problem. Avoid congestion.
Deliverable: Derivation of macroscopic models from the kinetic equation.
Practical Importance: So far, results are theoretical, given suggestions to improve traffic movements used in developed countries. In the future we plan to use in practice
The methods used in the work: Methods of probability theory, modeling techniques, programming methods.

МАЗМҰНЫ
КІРІСПЕ 7
1 СВЕТОФОР 2.0, TRANSCAD ЖӘНЕ TRANSMODELER АҚПАРАТТЫҚ ЖҮЙЕЛЕРІНДЕ БАҒДАРШАМДЫ АЛЬТЕРНАТИВТІ БАСҚАРУДЫ ТАЛДАУ 8
1.1 СВЕТОФОР 2.0 компьютерлік бағдарламасы 8
1.2 TransModeler трафик пакетінде бағдаршам сигналдарын альтернативті түрде басқаруды талдау 8
1.3 TransCad географиялық ақпараттық жүйесінде көлік ағымының қозғалысын бақылау 11
2 КӨЛІК АҒЫМЫН ТАЛДАУҒА АРНАЛҒАН ҚАЖЕТТІ МАТЕМАТИКАЛЫҚ ТҮСІНІКТЕР МЕН ДЕРЕКТЕР 13
2.1 Макроскопиялық модельдер 13
2.1.1 Лайтхилл-Уизем-Ричардс моделі 13
2.1.2 Танака моделі 20
2.1.3 Уизем моделі 21
2.1.4 Пэйн моделі және оның жинақталуы 21
2.1.5 Кинетикалық модельдер 21
2.1.6 Стохастикалық модельдер 22
2.2 Микроскопиялық модельдер 22
2.2.1 Ньюэллдің тиімді жылдамдық моделі 23
2.2.2 Трайбераның ақылды жүргізуші моделі 24
2.2.3 Клеткалы автомат модельдері 26
3 БАҒДАРШАМ ТУРАЛЫ ЕСЕП 32
3.1 Бағдаршам түсінігі 32
3.2 Бағдаршамның жұмыс істеу принципі 32
3.3 Бағдаршам туралы есеп (ҚАНДАЙ ЖАҒДАЙДА БАҒДАРШАМ АЛДЫНДА КЕПТЕЛІС ОРЫН АЛМАЙДЫ) 35
ҚОРЫТЫНДЫ 38
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 39

Қысқартылған сөздер тізімі

LWR моделі - Лайтхилл-Уизем-Ричардс моделі
АТҚ - Автокөліктік транспорттық қозғалыс
АЖ - Ақпараттық жүйелер
ST - Sim Traffic
ГАЖ - Географиялық ақпараттық жүйесі
ОЖ - Операциялық жүйелер

Анықтамалар

Бағдаршам - жарықпен белгі беру арқылы көшедегі, автомобиль жолы мен темір жолдағы қозғалысты реттеуге арналған құрылғы.
Кептеліс - жолдың өткізу мүмкіндігінен ағын тығыздылығының жоғары болғандыктан, көлік ағынның жылдамдылығының нөлге дейін түсуіне сәйке келетін күй.
Көлік, көлік кешені - экономиканың инфрақұрылымын қалыптастыратын салалардың бірі.
Жолаушы ағымы - белгілі бір уақыт көлеміндегі бір бағытта тасымалданған жолаушылар санын анықтайтын көлік өнімінің өлшеуіші.

КІРІСПЕ

Сіз бен біз күнделікті өмірде бағдаршам сынды адамзаттың кезекті таңғажайып өнертабысымен жиі ұшырасып қалып жатамыз, оның көмегіне жүгінеміз. Ал сол аталған бағдаршамның тамыры мен дамуы, жұмыс жасау принципі туралы мәліметтерді жете біле бермейміз. Математикалық тұрғыдан қарағанда бағдаршамның жұмыс жасау әрекетіне, кептеліс орын алған кездегі тиімді шешімді табуға бағытталған нақты есептеулер қолданылады.
Мен өзімнің дипломдық жұмысымда ең алдымен бүгінгі таңда өзекті мәселелердің бірі-бағдаршам қызметін жақсарту арқылы кептеліс пен басқа да жол апаттарын болдырмаудың жолдарын қарастырдым. Және де транспорттық көлік ағымын талдауға қажетті математикалық түсініктер мен деректерге, яғни макроскопиялық, микроскопиялық моделлерге, физиктер мен математиктердің көлік ағымының қозғалысын бақылауға, бағдаршам сигналдарының жұмыс істеу моделіне бағытталған есептеулеріне аса тоқталып өттім. Сонымен қоса, географиялық ақпараттық жүйелердің ішіндегі ең кең қолданыс тапқандарын зерттедім.
Әдетте көлік ағымы, кептеліс және бағдаршам қаз қатар жүретін түсініктер болып табылатыны хақ. Сондықтан мен бағдаршам туралы есепке тоқталмас бұрын транспорттық көлік ағымын сипаттап, кептеліс орын алған жағдайдағы шешімге қол жеткізуді ашып көрсетуді жөн көрдім.
Жұмыстың негізгі бөлімінде макроскопиялық моделдердің негізгі түрлері келтірілген, әсіресе біржолақты транспорттық көлік ағымына мысалдар жиі кездеседі.Гидродинамикалық аналогияларға терең назар аударылған.Бұл бөлімнің кілттік түсінігі сақталу заңына арналған транспорттық көлік ағымын суреттейтін бастапқы Коши есебінің жалпы шешімі болып табылады. Атап айтқанда, Лайтхилл-Уизем-Ричардс моделіне жете тоқталдым. Бұл макроскопиялық модел транспорттық көлік ағымы қозғалысының динамикасын есептеудегі тапсырмас дүние болып табылады. Және бұл модел біз қарастырып отырған макроскопиялық моделінің айырмалық және дифференциалды-айырмалық аналогы болып табылады. Сонымен қоса Танака моделіне, Пэйн моделіне, Уизем моделіне және олардың жинақталуына назар аударылған.
Транспорттық көлік ағымы қозғалысы мен кептеліс жағдайын анықтаған соң бағдаршамның осы аталғандармен қай уақытта тиімді және қай уақытта тиімсіз қызмет ететіндігін зерттедім. Әсіресе қандай жағдайда бағдаршам алдында кептеліс орын алмайтындығын көрсететін есепке тоқталдым.

1 СВЕТОФОР 2.0, TRANSCAD ЖӘНЕ TRANSMODELER АҚПАРАТТЫҚ ЖҮЙЕЛЕРІНДЕ БАҒДАРШАМДЫ АЛЬТЕРНАТИВТІ БАСҚАРУДЫ ТАЛДАУ

1.1 СВЕТОФОР 2.0 компьютерлік бағдарламасы

Бағыты
Автокөліктер санының күннен күнге артуы қалалардағы жол жүйесінің жұмысын қиындатты. Автокөліктер санының артуы қаладағы бағдаршам санына тікелей әсер етеді. Сондықтан бүгінгі таңда жол жүйесін реттеудегі маңызды бөліктің бірі-жол тораптарын қалыпқа келтіру болып саналады.
Алайда жол тораптарын реттеу бүгінде жеткілікті емес. Ең алдымен, Біз бағдаршам жұмысының кешенді тиімділік бағасын анықтауымыз қажет.
Жол тораптарын реттеу үшін сапалы есептеулер қажет. Осы мақсатта қазірігі таңда Светофор 2.0 бағдарламасы бізге қол ұшын бере алады. Бұл бағдарлама американдық Highway Capacity Manuаl 2000 жол тораптарының тиімділігін анықтайтын әдістемесі негізінде жасалған. Ол Ресей жолдарына икенделу мақсатында өзгертілген.
(2.0) нұсқасы бағдаршам сигналының жұмыс істеу тәртібін AutoCad бағдарламасында түрлендіруге мүмкіндік береді. Енді тек визуалды басқарудағы жасыл сигнал ұзақтығы мен оны реттеудегі жобалаудың қалпын көруге ғана болмайды, сонымен қоса жобалау нәтижелерін AutoCad бағдарламасы арқылы баспаға жіберуге болады.
Соңғы (2.0) нұсқасы жол торабындағы көліктер ұзындығын анықтауғы мүмкіндік береді. Ол желілік кептелістерді болдырмаудың таптырмас құралы болып саналады.
Желілік кептеліс - жол торабындағы кезек ұзындығы келесі қозғалыс болып жатқын жол торабын жауып қалу.
Светефор 2.0 бағдарламасымен жұмыс істеу
Жаңа файл құру немесе өзге дайын файлдарды ашу үшін бірінші жұмыс терезесінде жол тораптарына жақындауға мүмкіндік береді. Бұл кезең келесі батырмалар арқылы іске асады:
- жол торабына жаңа жақындау тәсілін табу
- жақындау тәсілін жою
- өзгертулерді сақтау
Осы және өзге кезеңдерде жоба файлын сақтау үшін келесі батырма қолданылады:
- жоба файлын сақтау

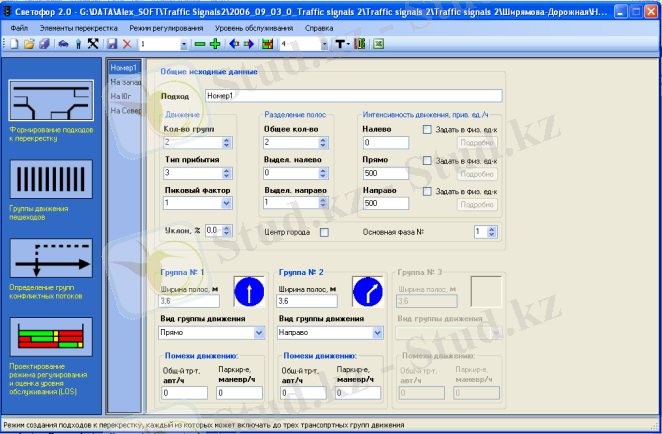
1.1-сурет. Жол торабына жақындау тәсілін жасау терезесі

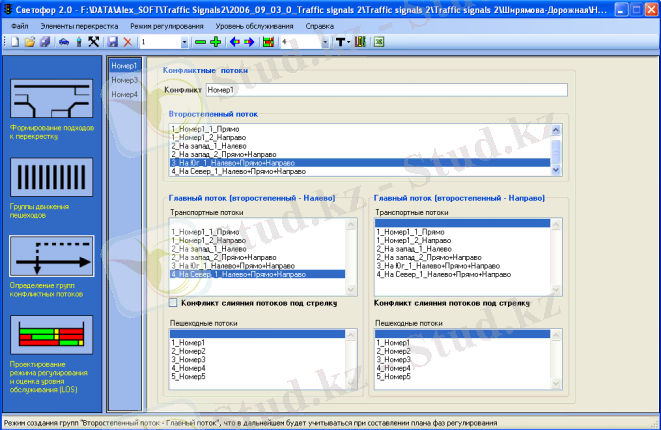
1.2-сурет. Басымдылық ережелерін анықтау терезесі

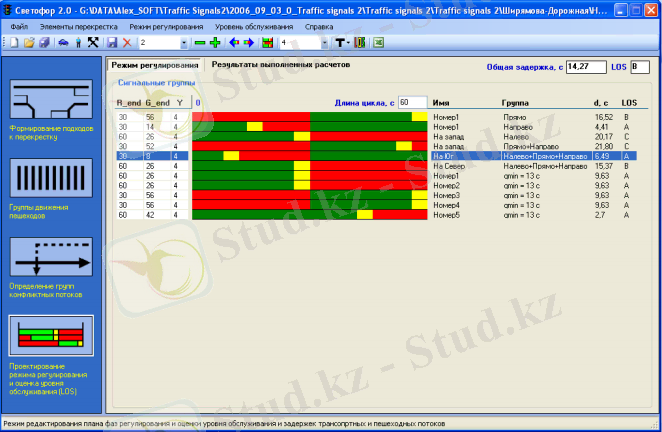
1.3-сурет. Қалыпқа келтіру тәртібін жобалау терезесі

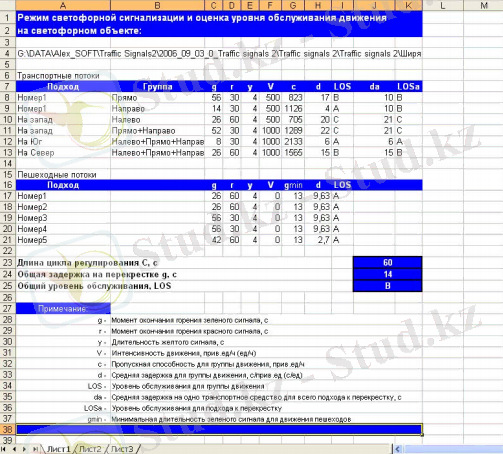
1.4-сурет. Есептеулерді MS Excel-ге экспорттау

1.2 TransModeler трафик пакетінде бағдаршам сигналдарын альтернативті түрде басқаруды талдау

TransModeler моделдеудің мықты және әмбебап трафик пакеті болып табылады. Қозғалысты жобалау және есептерді модельдеуінің кең спектріне қолданылады. TransModeler автожолдардан орталық мөлтек аудандарға дейінгі көлік желілерін имитациялай алады. Және де жол мультимодальді желілердің кең аймағын жоғары нақтылықпен және егжей-тегжейлі талдай алады. Біз ағым динамикасының бағасын, бағдаршам сигналын және оның қызметін, сонымен қоса желінің ортақ өндірімділігін үйлестіру үшін географиялық ақпараттық жүйенің (ГАЖ) 2-лік және 3-тік ортада қиын жүйелердің қозғалысын моделдей және елестете аламыз.
TransModeler қиын қосымшаларды жеңіл қолданудағы жаңа көкжиектерге әкеледі.Ол АҚШ-тағы ең танымал TransCad программалық жабдықтамасымен интеграцияланады.
Соңғы зерттеулер негізінде, TransModeler трафикті моделдеуді жаңа заманауи бейнеге келтіру мақсатында озық әдістемелік әдіс-айланы және бағдарламалық технологияны пайдаланады. TransModeler модлдері тарихи немесе жолға байланысты модельді уақытқа негізелген жүргізушінің динамикалық жол бағдарынан көрініс табады.
Ол қоғамдық көлікті, автокөліктер мен жүк көліктерін имитациялайды, оған қоса ал платаны электронды құрастыру, қозғалысты бақылау,анықтау секілді мүмкіншіліктерінің кең спектрін өңдейді.TransModeler сапар сұранысын болжамдау бағдарламалық қамсыздандыруымен жұмыс істейді, ол көліктік жоба мен жоспардың оперативті анализін орындауға арналған. Трафикті модельдеуінің нәтижелері кейін сапар сұранысын болжамдау үшін кері қолданыла алады.
Қолданудағы жеңілділік
Суппорт Corporation, географиялық ақпараттық жүйелер мен көлік саласындағы жетекші программалық жабдықтама болып табылады. TransModeler жол инженерлері мен кескіндеушілері қолдануға жеңіл болу үшін құрастырылған. TransModeler қолданушы интерфейсі түсінуге өте жеңіл және Windows стандарттарын толық қамтамасыз ететін жалғыз модельдеудің программалық жабдықтамасы болып есептеледі.
TransModeler бірнеше жобаларды, желілер,сұраныс көрінісін құрастыру мен басқаруға, бағдаршам сигналдарын альтернативті түрде басқаруды талдауға мүмкіндік береді. TransModeler келесі мүмкіндіктерге ие:
Corsim және SimTraffic-тен модельдеу мәліметтерін импорттау;
Бірнеше тізім үшін әртүрлі кіру файлдарын басқару;
Жергілікті масштабта трафик операцияларын имитациялау үшін үлкен желі-лердің ішкі облыстарын экспорттау.

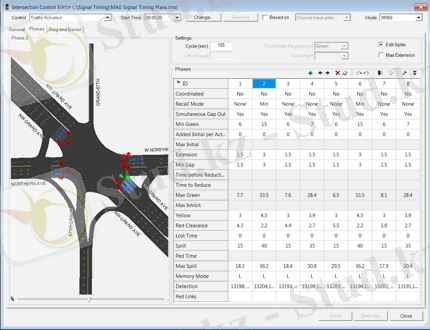
1.5-сурет. TransModeler трафик пакетіндегі жолдарды толтыру сұлбасы

TransModeler SE талапты есептемелік тапсырмаларды орындайтын, техникалық программалық жабдықтаудың жоғары өнімділігі болып табылады.
Сәйкесінше, біз ең жылдам, қарапайым бағаланған кез келген уақыт моментінде қол жетімдісін таңдауды ұсынамыз. TransModeler Windows 7 қажет етеді.
Операциялық жүйесі
Windows 7 немесе Windows 8. Біз 64-разрядтық ОЖ ұсынамыз, сондықтан сіз қосымша жадқа TransModeler SE-дің жаңа 64-разрядты нұсқасы арқылы қол жеткізе аласыз.
TransModeler SE ең жылдам процессорлерге тиімді, және біз үлкен модельдермен жұмыс үшін 4, 6 немесе 8-ядролық, 1 немесе 2 прцессорлық машиналарды ұсынамыз. TransModeler SE көпағымды кілттік процедуралар, бейнелерді автоматты тану бар және бірнеше ядро мен бірнеше процессорлар артықшылығына ие.
Процессор (CPU)
Жұмыс станциялары үшін біз Intel Haswell және Ivy Bridge процессорларын ұсынамыз (Core i7 және Xeon E3-1200 және E5-2600 үшінші және төртінші буындары ), себебі олар Intel Core 2 ескі процессорларымен салыстырғанда өнімділіктің маңызды жетілдірулерін ұсынады. Core i7 және Xeon 35003600 және 55005600 екінші буындағы сериялары, сондай-ақ, тиімді нұсқалар. Негізгі
үстел үстілік i5 процессорлары да қанағаттандырарлық, алайда аздап баяулау.
Қазіргі уақытта біздің жұмыс станциялардың жылдам компьютерлері екі 3.1GHz E5-2687W 8-ядролық процессоры барDell T7600, 192 Гбайт жады және 64-битті Windows 7 Professional.
Ноутбуктар үшін біз ең жылдам Haswell мобильді төрт ядролы i7s радиаторларын ұсынамыз,себебі олар аккумулятордың едәуір ұзақ қызмет уақытына ие және жұмыс үстелі сияқты жылдам болуы мүмкін.

Қозғалысты басқару
TransModeler бағдаршам мен әртүрлі интеллектуалды көліктік жүйелер (ИКЖ) сигналдарын имитациялайды.
Жол сигналдары:
TransModeler жол сигналдарын басқарудың ауқымды спектрін имитациялайды:
# Бағдаршам сигналдарының ортақ жүйелерін имитациялау, сонымен қоса сигналды басқару жетегін қозғалысқа келтіру;
# Бағдаршам сигналдарын басқарудың тым қиын жүйелерін имитациялау, сонымен қоса басқару жетегімен келісілген және үйлестірілген;
# Тасымалдау стратегиясының моделі мен көлік құралдарын апаттық қолданылу сигналдары басымдылыққа ие;
# Диаграмманың фазалық топтар, тұжырымдама бөгеттері және сақина негізінде немесе сигналдық реттеушілерді іске қосу үшін келтіріліп отырған шаблондарды қолдану керек.

1.6-сурет. Қала ішіндегі қозғалыс сұлбасы

1.3 TransCad географиялық ақпараттық жүйесінде көлік ағымының қозғалысын бақылау

TransCad ең алғаш және жалғыз географиялық ақпараттық жүйе болып табылады (ГАЖ), оны мамандар арнайы көлік қозғалысы туралы мәліметтерді сақтау, көру, басқару және саралау үшін жасап шығарған.
TransCad географиялық ақпараттық жүйе мен транспорттық көлік қозғалысының моделлеу мүмкіндіктерін бір интеграцияланған платформасын қамтиды.
TransCad кез келген көлік түріне, кез келген масштабта және бөлшектеу деңгейінде қолданыла алады.
TransCad ұсынады:
* тасымалдауға арналған арнайы мүмкіндіктері бар сапалы ГАЖ қоздырғышы;
* көлік қондырғыларын көруге, саралауға арналған құрылғылар;
* маршрутизациялауға, саяхаттау сұранысын жобалауға, қоғамдық көлікке, логистикаға, аймақтың орналасуы мен оны басқаруға арналған программалық модульдер.
TransCad нұсқалары:
TransCad екі нұсқада жасалған: Standart (немесе толық TransCad) және TransCad негіздері. TransCad негіздері дәл Standart TransCad жасалған программалық жабдықтамасы арқылы құрылған.
TransCad өзге ГАЖ, САПР және мәліметтер қорымен қолданыла алады
Мәліметтерге кіру: TransCad өз мәліметтерін қолдана отырып карта жасауға мүмкіндік береді. Егер сіз өз мәліметтеріңізді Excel парағында, Access кестелерінде, файлдар мәліметтер базасында немесе Oracle, SQL Server сияқты кез келген ODBC мәліметтер көзіне сәйкес файлдарда сақтасыңыз, онда TransCad сіздің мәліметтеріңізбен жұмыс жасай алады. Мастер мини- картасын жасау мәліметтерді бейнелеу, георграфиялық анализдеу және орналастыру мүмкіндіктерін береді.
TransCad транспорттық кәсіпқойлар қолданатын, транспорттық мәліметтерді сақтауға, бейнелеуге, басқаруға және анализдеуге арналған алғаш және жалғыз Географиялық ақпараттық жүйе (ГАЖ). TransCad кез келген басқа пакет бойынша теңдесі жоқ мүмкіндіктерді қамтамасыз ете отырып, біріктірілген платформа негізінде, Географиялық ақпараттық жүйесін модельдеудің транспорттық мүмкіндіктерімен үйлестіреді.TransCad транспорттың кез келген түрі үшін, кез келген масштабта қолданыла алады. TransCad келесі мүмкіндіктерді қамтамасыз етеді:
Тасмалдауға арналған арнайы кеңейтулері бар қуатты ГАЖ қозғалтқыш;
Транспорттық қосымшаларға арналған бейнелеу, сипаттау және анализ жасау құрал-саймандарын;
Бағдарлауға, саяхат сұранысын болжауға, қоғамдық транспортқа, логистикаға, орналасуға және аймақтарды басқаруға арналған программалық модульдерді қамтамасыз етеді.
Операциялық жүйесі
Windows 7 немесе Windows 8. Біз 64-разрядтық ОЖ ұсынамыз, сондықтан сіз қосымша жадқа TransModeler SE-дің жаңа 64-разрядты нұсқасы арқылы қол жеткізе аласыз.
TransModeler SE ең жылдам процессорлерге тиімді, және біз үлкен модельдермен жұмыс үшін 4, 6 немесе 8-ядролық, 1 немесе 2 прцессорлық машиналарды ұсынамыз. TransModeler SE көпағымды кілттік процедуралар, бейнелерді автоматты тану бар және бірнеше ядро мен бірнеше процессорлар артықшылығына ие.
Процессор (CPU)
Жұмыс станциялары үшін біз Intel Haswell және Ivy Bridge процессорларын ұсынамыз(Core i7 және Xeon E3-1200 және E5-2600 үшінші және төртінші буындары ), себебі олар Intel Core 2 ескі процессорларымен салыстырғанда өнімділіктің маңызды жетілдірулерін ұсынады. Core i7 және Xeon 35003600 және 55005600 екінші буындағы сериялары, сондай-ақ, тиімді нұсқалар. Негізгі үстел үстілік i5 процессорлары да қанағаттандырарлық, алайда аздап баяулау.
Қазіргі уақытта біздің жұмыс станциялардың жылдам компьютерлері екі 3.1GHz E5-2687W 8-ядролық процессоры барDell T7600, 192 Гбайт жады және 64-битті Windows 7 Professional.
Ноутбуктар үшін біз ең жылдам Haswell мобильді төрт ядролы i7s радиаторларын ұсынамыз,себебі олар аккумулятордың едәуір ұзақ қызмет уақытына ие және жұмыс үстелі сияқты жылдам болуы мүмкін.

2 КӨЛІК АҒЫМЫН ТАЛДАУҒА АРНАЛҒАН ҚАЖЕТТІ МАТЕМА-ТИКАЛЫҚ ТҮСІНІКТЕР МЕН ДЕРЕКТЕР

2.1 Макроскопиялық модельдер

Бұл тарауда макроскопиялық моделдердің негізгі (тарихи және мүмкін болатын қосымшалар тұрғысынан алғанда) түрлері келтірілген, әсіресе біржолақты транспорттық көлік ағымына мысалдар келтірілген. Гид-родинамикалық аналогияларға терең назар аударылған.Бұл бөлімнің кілттік түсінігі сақталу заңына арналған транспорттық көлік ағымын суреттейтін бастапқы Коши есебінің жалпы шешімі болып табылады.

2.1.1 Лайтхилл-Уизем-Ричардс моделі

ХХ ғасырдың 40 жылдарының екінші жартысы мен 50 жылдары КСРО мен АҚШ жарылғыш заттың атылуы кезінде пайда болатын үдерістерді зерттеумен қарқынды айналысқан. Сонымен қоса сақталу заңының теңдеулеріне арналған бастапқы-шеткі есепті (және осындай теңдеулер жүйесін) байқауға көп көңіл бөлінген. Осы уақытта осыған ұқсас теңдеулер кездесетін қосымшалардың артуы байқалған. Осылайша 1955 жылы тәуелсіз зерттеулер барысында алғашқы біржолақты (жол екі жаққа қарай шексіз, қозғалыс солдан оңға қарай (анықтылық үшін), ешқандай автокөліктік құралдар ағыны жоқ) транспорттық көлік ағымының макроскопиялық (гидродинамикалық) моделі ұсынылып, кейіннен Лайтхилл-Уизем-Ричардс моделі атанды (осы модельді жиі Лайтхилл-Уизем1 моделі деп атайды).
Лайтхилл-Уизем-Ричардс моделінде келесілер бағамдалады:
Ағымның v(t,x) жылдамдығы мен ρ(t,x) тығыздығы арасында өзара бірмәнді тәуелділік бар;
АТҚ тығыздығының ρ(t,x) сақталу заңы орындалады. ρ(t,x) жазуы t уақытындағы х координаталы трасса нүктесінің маңайындағы ұзындық бір-лігінің АТҚ санын білдіреді. Кейде Уитемнің орнына Уизем деп атайды( С.П.Новиковтың еңбектерінде).
Яғни, v(t,x)-t уақытындағы х координаталы трасса нүктесінің маңайындағы АТҚ жылдамдығы. Ары қарай барлық жерде транспорттық көлік ағымы макроскопиялық модельдермен сипатталатын кеңістік масштабтары АТҚ-ға тән көлемді айтарлықтай асыратындығы болжанады.
Басқаша айтқанда, транспорттық көлік ағымы алдағы жағдайға байланысты АТҚ әрекеті жете суреттелген кейбір макроскопиялық модельдерге бағынады.
Және бұл модель біз қарастырып отырған макроскопиялық модельдің айырмалық және дифференциалды-айырмалық аналогы болып табылады. Осылайша ρ(t,x), v(t,x) анықтауға ұсынылған тәсілдің дұрыстығы макроскопиялық модельді микроскопиялыққа орнықты жуықтауға негізделген.

2.1-сурет. Транспорттық көлік ағымының қалып-күй теңдеуі

Бірінші жобалауды келесі шартпен көрсетеміз:

vt,x=Vρt,x. (1)

V(ρ) функциясына қатысты келесі жобаланады:

V'ρ0 (2)

мұнда Ԛ(ρ) = ρV(ρ) - АТҚ ағымының көлемі. Ԛ(ρ) тәуелділігін көбінесе іргелі (немесе негізгі) диаграмма деп атайды. Біржолақты ағым үшін Ԛ"(ρ)0 деп есептелінеді (мұны келесі түрде түсінуге болады: әртүрлі тығыздықтағы жолдардағы екі бірдей және тәуелсіз қозғалыс дәл осы жолдардағы бастапқы тығыздықтардың арифметикалық ортасына тең екі бірдей тығыздықтағы қозғалысқа қарағанда тиімсіздеу болады. Алайда егер бірнеше жолды бір жолға біріктірсе, онда шынайы өмірде көрсетілген көлік ағымының байқауларына сүйенсек Ԛ(ρ) ойыстығынан бас тартуға тура келеді.
Сурет 1. және Сурет 2. Мәскеу қаласының Көлік Инфраструктурасын Зерттеу Орталығының Автозавод көшесінен Варшавский шоссесіне дейінгі үшінші көліктік сақинаның аймағындағы төрт жолақ бойынша жиналған мәліметтер елтірілген. Негізінде V(Ԛ) тәуелділігі есептелінген еді.
АТҚ-ның бір жолдан екінші жолға орын ауыстыруы ағым көлемінің азаюына әкеледі ( бір жағынан орта бір жолдан екінші жолға орналасу тезірек қозғалуға мүмкіндік береді, алайда екінші жағынан орта есеппен мұндай тәсіл орын ауыстыруға қосымша шығын келтіреді, сонымен қоса бір АТҚ екіншінің алдына орын ауыстыру кезінде қозғалысты баяулатады).

2.2-сурет. Іргелі диаграмма

Екінші жобалауды сақталу заңымен келтірейік:

abρ(t+∆,x)dx-abρt,xdx= -tt+∆Qρτ,bdτ-tt+∆Qρτ,adτ. (3)

Сайып келгенде, t=0 жартылай жазықтығындағы кез келген тікбұрышты Г контурына келесі формула орындалады:

rρt,xdx-Qρt,xdt=0. (4)

ρ(t,x) тегіс нүктелерінде:

dρdt+d(vρ)dx=dρdt+d(Vρρ)dx=dρdt+dQ( ρ)dx=0. (5)

Бастапқы шарт түрін көрсетейік (Риман шартының түрі)

𝜌0,x=ρ- , xx-ρ0x, x-=xx+,ρ+, x=x+ (6)

Коши есебі (4), (5) кептеліс тарауын сипаттау кезінде пайда болады:
ρ0 - ′(x)0 , ρ+=ρmax болсын делік, мұнда ρmax - мүмкін болатын мак-сималды тығыздық, келесі мәселе транспорттық көлік ағымы бойынша алдағы кептеліс туралы мағлұматты қалай жіберуге болатынын анықтау керек.

2.3-сурет. Ажыраудағы R-H шарты

(3) арақатынасқа ораламыз. Осы арақатынас ρ(t,x) тығыздықты ажырау функциясына да орындалғанын атап өткен жөн. Оған қоса функция ажырауында ρ(t,x) - тығыздықтың кенет ұлғаюы байқалады, бұл кептеліс шекарасына сәйкес келеді. t уақытында ажырау х координата нүктесінде және ρ(t,x-0)=ρ- , ρ(t,x+0)=ρ+ болсын делік. Осы ажырауға (t;x) жазықтығында қисық L сай келсін деп қарастырайық. (t,x)ϵ L нүктелерінің маңайынан Сурет 3. көрсетілгенде тікбұрышты контур аламыз (анық болу үшін сағат тілі бойынша деп бағдарлаймыз). Сонда (3) арақатынас келесіні білдіреді:

0=r(ρt,xdx-Qρt,xdt-ρ+c-Qρ+∆t-(ρ-c-Q (ρ-))∆t+0(∆t). (7)

мұнда c=dxdt - (t,x) нүктесіндегі L көлбеуіне сәйкес келеді, ∆ t - t осіндегі контур проекциясының ұзындығы. ∆ t--0 болғанда бұл теңдік с ажырауының қозғалыс жылдамдығының келесі шартына айналады. Әдетте бұл шарт Гюгонио-Ранкин2 шарты деп аталады:

c=σρ+,ρ+=Qρ+-Qρ-ρ+-ρ-R-H. (8)
----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

----------------------------------- ----------------------------------- ----------

[2] Бұл шартты қосымша Гюгонио шарты деп те атайды. Ранкинның орнына Ренкин деп атайды.
(4) теңдеуінің әрқашан әлсіз шешімі болады екен (3) арақатынасты және (5) бастапқы шартты әлсіз мағынада қанағаттандырады). Бірақ келесі мысал көрсетіп отырғандай теңдеу сансыз көп шешімге ие бола алады, яғни бірмәнділік жоқ.

2.4-сурет. Ренкин шартының мысалы

Мысал. Хопф теңдеуін3 қарастырамыз

dρ dt+ρdρdx=0 (9)

және Риманның бастапқы шарты

ρ0,x=1, x=0-1, x0. (10)

ρqt,x=1, x=1-q2,-q, 1-q2,x=0 q, 0x= 1-q2,-1, 1-q2tx (11)

----------------------------------- ----------------------------------- ----------

3 Хопф теңдеуінде айнымалыларды және белгісіз функцияны ауыстыруды Лайтхилл-Уизем-Ричардс моделінде кездесетін атақты жағдай Гриншилдс моделінде көруге болады. Функция t 0 болған кезде (4) теңдеуді және (5) бастапқы шартты қанағаттандырады (ажырауларда R-H шартының орындалуын тексеру жеткілікті).
О.А.Олейник 1958 жылы ұсынған ажырау тұрақтылығының шарты ретінде жалғыз ғана шешім іріктеу шартын таңдайды.
Мысалы t=0 жартылай жазықтығындағы нүктеде анықталған кез келген q=1 болған жағдайда.
Ажырауда R-H шартынан өзге Е-шарты4 да орындалу керек:

∀ρ∈ρ-,ρ+--σρ-,ρ+=σρ-,ρ+, егерρ-ρ+
∀ρ∈ρ+,ρ---σρ-,ρ+=σρ-,ρ+, егер ρ-ρ+ (12)

2.5-сурет. Жылдамдық теңдеуі
----------------------------------- ----------------------------------- ----------

4 Бұл шартты қосымша энтропиялық шарт, О.А.Олейник энтропиялық шарты, Е - шартты О.А.Олейник деп те атайды.Е-шарты ( және R - H шарты ) қайдан пайда болғаны төменде аталып өтіледі.
Бөлшектік - тұрақты бастапқы шарттар класстарында Е - шартын ρ(t,x) динамикасын бірмағыналы және конструктивті анықтау арақатынасындағы мүмкін болатын ажырауларды іріктеу шарты ретінде қосылатынын атап өткен жөн.
x=0 нүктесінде бастапқы мәліметтердің ажырауын баттастырып қою арқылы, яғни x=δ бөлшегінен бөлек ρ(0,х) сәйкес келетін ρδ(0, х) - монотонды өспелі үздіксіз функцияны енгізу арқылы limδ--0+ρδt,x=ρ1(t,x) көре аламыз ( мысалы, мінездемелердің5 классикалық тәсілін пайдалану арқылы ).
Яғни ρ2(t,x) классикалық емес шешімі тұрақты шешім болып табылмайды. ρ2(t,x) шешімінің ажырауында Е-шарты орындалмайтындығын байқау қиын емес, сондықтан ρ2(t,x) шешім болып табылмайды.
Е-шарты геометриялық интерпретацияға ие ( анықтылық үшін ρ-ρ+ ):
Ԛ(ρ) функциясының графигі ρϵ(ρ-,ρ+) болған жағдайда ( ρ-,Ԛ(ρ-)) және( ρ+,Ԛ(ρ+)) нүктелері арқылы өтетін түзуден төмен жатқан жоқ. С ажырауының қозғалыс жылдамдығы осы түзудің көлбеуіне тең.

Мысал. Тағы да Хопф теңдеуін және бастапқы шартты қарастырамыз
ρ0,x=-1, x=01, x0. (13)
Коши есебінің (4), (5) келесі әлсіз шешімдері болуы мүмкін:

ρ1t,x=-1, x=-txt, -tx=t1, xt ρ2t,x=-1, x=01, x0 (14)

2.1.2 Танака моделі

1963 жылы Танакада ұсынылған V(ρ)тәуелділігін анықтаудың бір тәсілін мысал ретінде келтірейік.
Автокөлік құралдарының біржолақты ағымы қарастырылады. Тығыздық ρ(V)=1d(V) , мұнда d(V)=L+C1+C2V2 - Vағым жылдамдығы берілген автокөлік құралдарының арасындағы орташа (қауіпсіз) арақашықтық (сонымен қоса, d(V) динамикалық габарит немесе көріну дистанциясы деп те атайды), L - автокөлік құралдарының орташа ұзындығы , C1 - жүргізушілердің әрекетін сипаттайтын уақыт, C2 - тежегіш жолына пропорционалды коэффициент. d(V) тәуелділігінен (2) шартты қанағаттандыратын V(ρ) (1) тәуелділігін алуға болады.
C2 коэффициенті негізінде жолдағы шарттарға байланысты болады. Осылайша қалыпты шарттарда

dvм=5,7м+0,504c*vмc+0,0285c2м*v2м2c 2 (15)

Сулы асфальт үшін

dvм=5,7м+0,504c*vмc+0,0570c2м*v2м2c 2 (16)

Мұз басқан жол үшін

dvм=5,7м+0,504c*vмc+0,1650c2м*v2м2c 2 (17)

2.1.3 Уизем моделі

Келесі қадам жүргізушілердің көз қырағылығына байланысты болады:

vt,x=Vρt,x-D(ρt,x)ρ(t,x)dρ(t,x)dx, Dρ0; (18)

dρdt+dQ(ρ)dx=ddx(D(ρ)dρdx (19)

Оң жақ бөліктерінде пайда болған жаңа диффузиялық буындар ( (1) және (4) салыстырғанда) жүргізушілер алдағы көліктердің тығыздығы артқанда жылдамдықтарын азайтады және тығыздық азайғанда кері артатынына са келеді. Гидродинамикалық (макроскопиялық) модел (2), (5), (6) Уизем моделі деп аталады.

2.1.4 Пэйн моделі және оның жинақталуы

Пэйн моделі (1971ж) маңызды қадамдардың бірі болды. Бұл моделін сақталу заңы ретінде қараструға болады

dρdt+d(vρ)dx=0 (20)

бұл жерде жылдамдық тығыздыққа тәуелді болмайды деп жорамалданады. Жылдамдық үшін V шынайы жылдамдықтың қалаулы жылдамдыққа ұмтылу теңдеуі жазылады
Vρ-Dρρdρdx (21)
мұнда τ (τ~1 сек) - ұмтылу жылдамдығын білдіреді (электротехникалық терминологияда τ- тынығу уақыты)

ddtv=dvdt+vdvdx=-1τ(v-(Vρ-D(ρ)ρdρdx )) (22)

----------------------------------- ----------------------------------- ----------

5 (t,x) жазықтығындағы мінездемелер қауымының теңдеуі келесі түрде болады:
.dxdt=Q'(ρ(t,x)) Сондықтан ρ(t,x) функциясынан уақыт бойынша толық туынды мінездеме бойында бар: dρdt=dρdt=dρdxdxdt=dρdt+Q'ρdρdx=dρd t+dQ(ρ)dx=0,
яғни ρ(t,x)=const- мінездеме бойымен.
Алынған теңдеулер жүйесін қатаң гиперболалығы байқалады (ddх мат-рицасының әртүрлі өзіндік заттың мағынасы бар)6 .
Екі түрлі сақталу заңдарының жүйесіне глобальді уақыт бойынша жалпы шешімді қалай дұрыс анықтау керектігі белгісіз (Х.Пэйн жүйесі осындай жүйенің мысалы бола алады, оған қоса сызықтық емес оң жақ бар).
Жүйелерге арналған тұтқырлықтың жойылу тәсілі оң бөліктегі анықталған тура D(ρ)матрицасын таңдауға сезгіш болып келеді.
Алайда соңғы 15 жылда бір айнымал кеңістікті сақталу заңының қатаң гиперболалық жүйелерінде бірқатар алға басу байқалды.
Шешім ажырауларын баттастыру қалауы Лайтхилл-Уизем-Ричар моделінен Уизем моделіне алып келді. Және осы қалау Пэйн моделіне диффузиялық реттеулерді енгізуге түрткі болды. Осылайif Р.Кюн (1993), Кернер-Конхойзер(1994) және т.б. жаңа модельдер пайда болды.
Онда тығыздық пен жылдамдықтан басқа автокөлік құралдары жүргізушілерінің бір бөлігі ағым ішінде орын ауыстыру үшін тұрақты қозғалысты босатуға көмектесетін тұрақтылық параметрі бар.

2.1.5 Кинетикалық модельдер

Газдық динамиканың аналогиясын жалғастыра отырып И.Пригожин және Р.Херман 1961 жылы транспорттық көлік ағымын кинетикалық теңдеумен сипаттауды ұсынған (одан кейін 1975 жылы С.Павери-Фонтана, 1995 жылы Д.Хельбинг және т.б).
Кеңейтілген фазалық кеңістіктегі (t,x,V) тығыздық үшін жылдамдық пен кинетикалық теңдеудің келесі интеграцияланған жылдамдығы арқылы әртүрлі функцияларды көбейту - кинетикалық теорияда газдық днамиканың (гидродинамиканың) теңдеулері шығады. Осы сияқты көлік ағымының кинетикалық модельдерінен (көп жолақтыларды да қосқанда) макроскопиялық (гидродинамикалық) модельдерін шығаруға болады.
Кинетикалық және гидродинамикалық модельдердің ортасында аралық модельдер болады, оларды мезоскопиялық деп атайды.

----------------------------------- ----------------------------------- ----------

6 Келесі айтарлықтай деректі ескерген жөн: көлік ағымының гидродинамикалық моделлердің соларға ұқсас гидродинамикалық аналогтарынан басты айырмашылығы әдетте теідеулердің гиперболалық (қатаң) жүйелері мен олардың диффузиялық аналогтерінен пайда болатын оң жақ бөлігінде болып табылады. Бұл мүлтіксіз болып көрінеді. Себебі көліктік сұйықтық - оң жақ бөлікте болатын уәждемелі сұйықтық. Бұл ескерту көлік ағымдарының гидродинамикалық моделлерін есептеуде жарты ғасырдан астам уақытта құралған есептеу алгоритмдерін қолдануға мүмкіндік береді.
2.1.6 Стохастикалық модельдер

Жақында А.П.Буслаев және басқалармен көпжолақтықтарды зерттеудің қызықты идеялары ұсынылды.

2.2 Микроскопиялық модельдер

Бұл тарауда біржолақты транспортты ағындардың қозғалысын микроскоптиялық модельдеудің негізгі тәсілдері жайлы және микроскопиялық пен макроскопиялық модельдер арасындағы байланыс жайлы айту жоспарланған. Бәрінен бұрын, тиімді жылдамдық және көшбасшыға еру модельдері сипатталады. Сонымен қатар кең таралған модельдердің бірі (соңғы он жылда) - Трайбердің ақылды жүргізушімоделі де сипатталады. Осы бөлімнің қорытындысында қосымшаларды талап етілген клеткалы автоматтар(олар көбінесе белгілі макроскопиялық модельдердіңайырмалық аналогтары болып табылады) моделдері келтіріледі.

2.2.1 Ньюэллдің тиімді жылдамдық моделі

АТҚ біржолақты ағында солдан оңға қарай нөмірленген болсын. sn(t) aрқылы t=0 уақыт сәтіндегі n - АТҚ-ның ортасының координатасын белгілейік. Айталық

hn t=Sn+1 t-Sn t,Vn t=Sn' t. (23)

Ньюэллдің микроскопиялық моделінде (бұл модель 1961 ж. ұсынылды және тиімді жылдамдық модельдерінің алғашқыларының бірі болып табылады [1], [5]).

Sn' t+τ=Vnt+τ=V1hnt,V' p0, (24)

деп негіз етіп алынады (әр жүргізуші үшін көшбасшыға дейінгі арақашықтыққа байланысты қауіпсіз қозғалыс жылдамдығы болады) , мұндағы τ - жүргізушілер реакциясын сипаттайтын уақыт.

vt,Snt+vtt,Snt+vt,Sntvxt,Sntτ ≈Vρt,Snt+V'ρt,Sntρxt,Snt12ht,Snt,ht t,Snt+vt,Snthxt,Snt≈vxt,Sntht,Snt. (25)

Екінші теңдеуді - ρ2 көбейтіп және функцияның аргументтерін (t=0 жазықтығында жақын қисықтардыңесептік жиынтығынан ρ(t,x) және v(t,x) үзіліссіздік бойынша жалғастыра отырып) түсіре отырып келесі жүйеге келеміз:

V+Vt+VVxτ≈Vρ+V'ρ2ρ ρx, (26)

ρt+(vρ)x≈0. (27)

Осылайша, біз, [1] қолданып, τ және

Dρ=-V'(ρ)2 (28)

үшін жаңа интерпретация ала отырып, Пэйн моделін енгіздік. Егер біз басында τ=0 деп алсақ, онда жоғарыда айтылған операцияларды орындау нәтижесінде Уизем моделіне келетін едік. Егер тіпті V(ρ)-мен салыстыруда

V'ρρx12h (29)

қосылғышын елемесек (ескере кетейін, һ-ты аз шама деп есептейміз), Лайтхилл - Уизем - Ричардс моделін алатын едік.
Жоғарыда қолданылған әдісті автомодельді редукция деп атайды. Автомодельді редкцияның жақсы мысалы ретінде нөлдік массалары бар бірдей (ұзындықтары мен қаттылықтары белгілі) серіппелермен байланысқан (шеттері бекітілген) қыл тербелісі моделінен шығатынкөптеген бірдей (массалары белгілі) шарлардан тұратын толқынды теңдеудің Д'Аламбер жасаған (1980) қорытындысын айтуға болады. Әрбір шардың қозғалысы Ньютонның екінші заңымен сипатталады (шардың и тепе-теңдік күйінен ауытқуы үшін) және тек қана көршілес шарлардың жағдайларына тәуелді ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.