Маскет-Леверет (MLT) жылу моделі: автомодельді шешімдердің сандық-аналитикалық зерттелуі және сапалық қасиеттері


Қазақстан Республикасының Білім және Ғылым министрлігі
Абай атындағы Қазақ Ұлттық Педагогикалық Университеті
Математикалық талдау кафедрасы
ТҮЛЕКТІК ЖҰМЫС
Тақырыбы
Маскет - Леверет теңдеуінің автомодельді шешімі туралы
Алматы 2009
МАЗМҰНЫ
Кіріспе
Гидродинамика теңдеулерінің автомодельді
шешімдерінің қолданылуы . . .
1-ТАРАУ. ЕКІ ФАЗАЛЫ ЖЫЛУ АРҚЫЛЫ СҮЗГІЛЕУДІҢ ЕСЕПТЕРІН САНДЫҚ-АНАЛИТИКАЛЫҚ ТӘСІЛ АРҚЫЛЫ ЗЕРТТЕУ . . .
1. 1. Мұнай қабаттарына жылу арқылы әсер ету . . .
1. 2. Маскет - Левереттің жылу моделі (MLT-моделі) . . .
1. 3. Автомодельді шешімдердің теориясы . . .
1. 4. Сандық зерттеу . . .
2-ТАРАУ. MLT-МОДЕЛІНІҢ АВТОМОДЕЛЬДІ ШЕШІМДЕРІНІҢ САПАЛЫҚ ҚАСИЕТТЕРІ . . .
2. 1. Маскет - Левереттің жылу моделі . . .
2. 2. Параболалық типтегі автомодельді шешімдер . . .
2. 3. Соңғы жылдамдықтың интерпретациясы . . .
2. 4. Ұңғыманың әсер ету зонасы . . .
2. 5. Коэффициенттердің термодинамикалық қасиеттері . . .
2. 6.
 су қанығуының монотондылық шарттары . . .
су қанығуының монотондылық шарттары . . .
Қорытынды бөлім . . .
Пайдаланған әдебиеттер . . .
Гидродинамика теңдеулерінің автомодельді шешімдерінің қолданылуы
Барлық мұнай өндіру технологиясының есептеу әдістерінің болжауы бойынша мұнай қорының орналасқан жері симметриялық базистік элементтерге қарай бөлінуі тиіс және де олар скважиналардың үзіліссіз орналасуына сай келуі керек. Базистік элементтер негізінде анализ жасау процесі мұнай өндіру саласында барлық өндірістік технологиялық схемалардың алғы шарты болып табылады. Базистік элементті симметриялық шарттары бар, скважиналардағы берілген аймақтарда жер қыртысының біртекті жүйелерінде сол элементтің шектеулі және тұйық жүйелері ретінде қарастыруға болады. Ең соңында барлық алынған базистік көрсеткіштерге сай өндіріс орнына арналған есептеулер жүргізіледі.
Әрбір базистік элементтегі біртекті емес сұйықтықты қуыс ортада сүзгілеуден өткізе отырып, бірөлшемді модельді жерасты гидродинамикасы арқылы сипаттау мұнай өндіру саласының автоматтандырылған басқару процесінің негізін қалайды. Сондықтан да көптеген зерттеушілер жерасты гидродинамикасының бірөлшемді сандық модельдерін зерттеу мен негіздеуге көбірек көңіл бөледі.
Мұнай өндіру процестерінде инженерлік регуляр тәсілдерін қолдануда гидродинамикалық модельдер негізгі рөл атқарады. Олар бірөлшемді модельдерді дәлдікпен есептеу және тұрақты шешім қабылдау, параболалық типтегі және сырғымалы толқындар типіндегі автомодельді шешім қабылдау негізін қалайды.
Гидродинамика теңдеулерінің автомодельді шешімдері кеңінен қолданылады:
- теңдеулердің негізгі шешімі ретінде қызығушылық тудырады;
- жалпылама теңдеулердің жуықтап есептеу тәсілдерін құрғанда негізгі эталон ретінде пайдаланылады;
- алдын ала негізгі теңдеулердің сандық және аналитикалық негіздерін зерттеуге қолданылады;
- кең көлемдік тапсырмалардың шекаралық және бастапқы шарттарының құрылымы есептелмей қалған көптеген жағдайларда бұл асимптотикалық көзқарас қалыптастырады, ал бұл аймақ кейде өте қызықты болып келеді;
- теоремамен байланыстыра отырып салыстырғанда айнымалы негіздерді сапалы есептеуге арналған теоретикалық зерттеу аппаратын береді;
- кейбір қолданбалы аймақтарда (мысалы, мұнай өндірісінде) болжауды бағалау құралы ретінде қолданылады.
1-ТАРАУ
ЕКІ ФАЗАЛЫ ЖЫЛУ АРҚЫЛЫ СҮЗГІЛЕУДІҢ ЕСЕПТЕРІН САНДЫҚ-АНАЛИТИКАЛЫҚ ТӘСІЛ АРҚЫЛЫ ЗЕРТТЕУ
Бұл бөлімде мұнай қабаттарын екі фазалы жылу арқылы сүзгілеудің термогидродинамикалық процестерін сандық-аналитикалық тәсілмен зерттеу қарастырылады.
- Мұнай қабаттарына жылу арқылы әсер ету.
Өте қою және парафин аралас мұнай көздері мен құрамы өте нашар жеңіл (сұйық) мұнай көздерін өңдеуде жылу арқылы сүзгілеу өте тиімді және дайындалған технологиялық әдіс болып табылады. Мұнай қабатына жылу арқылы әсер етудің басты мақсаты мұнайға жылу арқылы әсер етіп, оның қоюлығын азайтып жылжымалылығын арттыру болып табылады. Ал парафин аралас мұнай үшін парафинді қуыстарда кристалл күйіне айналдырмас үшін жылумен әсер етеді.
Жылу технологиясының екі түрі бар: мұнай айдайтын ұңғымалар арқылы су буы немесе ыстық сумен мұнайды сығымдау және мұнай өндіріліп жатқан ұңғымаларды жылу буы арқылы өңдеу.
Мұнайды жер қатпарынан шығаруда жылу технологиясының әртүрлі гидродинамикалық схемалары пайда болады: мұнай айдау мен өндіру ұңғымалары бір бағытта сығымдап, мұнай қабатын жылыту мен суыту арқылы; ұңғымаларда тоқтаған кезде жылу капилярлығын сіңіру арқылы; мұнайдың тұнба аймақтарын ағызу және т. б.
Мұнайдың күрделі жылу технологиясын тек қана инженерлік есептер арқылы пайдалану практика жүзінде мүмкін емес және жаңа математикалық модельдеу тәсілдерін пайдалануды қажет етеді.
1. 2. Маскет Левереттің жылу моделі (MLT-моделі)
Бір өлшемді MLT моделінің теңдеуі біртекті изотроптық қуыс ортадағы тұрақты динамикалық су қаныққандығы
 , бірқалыпты температура
, бірқалыпты температура
 және орташа қысым
және орташа қысым
 үшін өрнектегенде мына түрде болады:
үшін өрнектегенде мына түрде болады:
 (1)
(1)
мұндағы
 екі фазалы сұйықтықтың толық шығыны. (1) теңдеулер жүйелерінің коэффиценттері
екі фазалы сұйықтықтың толық шығыны. (1) теңдеулер жүйелерінің коэффиценттері
 және
және
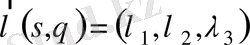 MLT моделінен шығатын функционалды параметрлерден анықталады және олардың физикалық мағынасына келсек, олар мынандай қасиеттерге ие болады:
MLT моделінен шығатын функционалды параметрлерден анықталады және олардың физикалық мағынасына келсек, олар мынандай қасиеттерге ие болады:
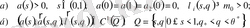
а
) қасиеті
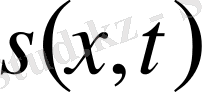 және
және
 үшін сәйкес параболалық және теңөлшемді параболалық теңдеулерді қамтамасыз етеді және де
үшін сәйкес параболалық және теңөлшемді параболалық теңдеулерді қамтамасыз етеді және де
 (
t -
параметр) үшін жай теңдеулердің туындамауын қамтамасыз етеді.
(
t -
параметр) үшін жай теңдеулердің туындамауын қамтамасыз етеді.
1. 3. Автомодельді шешімдердің теориясы
MLT-моделі мен Маскет Левереттің екі фазалы изотермиялық сүзгілеу модельдері сияқты математикалық модельдерді пайдалану өте күрделі математикалық аппаратты талап етеді. Практикада қарапайым және еркін қолданылатын тәсілдер өте бағалы болып табылады. Сондай жолдардың бірі ретінде модельдің дәл есептелген теңдеулері негізінде жер қатпарындағы мұнай қабатын жуықталған формулалармен сығымдауды сипаттау осы уақытқа дейін практикада табысты қолданылып келеді. Оларға тек
х
айнымалысына тәуелді стационар шешімдер,
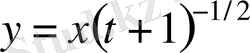 -не тәуелді параболалық типтегі автомодельді шешімдер,
-не тәуелді параболалық типтегі автомодельді шешімдер,
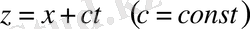 тәуелді жылжымалы толқындар және т. б шешімдер жатады. М. Маскеттің (сығымдау заңдары), И. А. Чарнойдың (ұңғыманың әсер ету зонасы) параболалық автомодель негізінде құрылған қарапайым формулалары осы уақытқа дейін мұнай кен орындарында изотермиялық тәсілдердің инженерлік анализін өңдеудің құралы болып есептеледі.
тәуелді жылжымалы толқындар және т. б шешімдер жатады. М. Маскеттің (сығымдау заңдары), И. А. Чарнойдың (ұңғыманың әсер ету зонасы) параболалық автомодель негізінде құрылған қарапайым формулалары осы уақытқа дейін мұнай кен орындарында изотермиялық тәсілдердің инженерлік анализін өңдеудің құралы болып есептеледі.
Жоғарыда айтылғандарды ескере отырып мұнай қабатына жылу тәсілдерінің әсер етуін жай дифференциалдық теңдеумен өрнектелген MLT моделінің аналитикалық (автомодельдік) шешімдерін табудан бастаймыз. Мынандай жағдайда қарастырамыз, (1) теңдеуде қоспаның толық шығыны
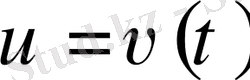 берілген және бұл қоспаның бір бағыттағы жылжуы жылу технологиясының режимдеріне сай келеді. Осыдан кейін
берілген және бұл қоспаның бір бағыттағы жылжуы жылу технологиясының режимдеріне сай келеді. Осыдан кейін
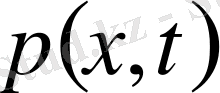 функциясына тәуелсіз
функциясына тәуелсіз
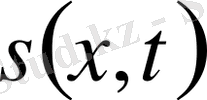 ,
,
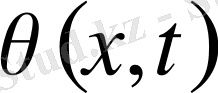 функциялары табылуы мүмкін. Шарт бойынша
функциялары табылуы мүмкін. Шарт бойынша
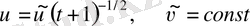 берілген (бұдан ары қарай
берілген (бұдан ары қарай
 -ның үстіндегі толқынды түсіреміз) , енді (1) жүйенің тек
-ның үстіндегі толқынды түсіреміз) , енді (1) жүйенің тек
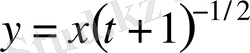 тәуелсіз бір айнымалыға тәуелді
тәуелсіз бір айнымалыға тәуелді
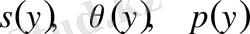 параболалық типінің автомодельді шешімін табуға болады және олар келесі теңдеулерді қанағаттандырады:
параболалық типінің автомодельді шешімін табуға болады және олар келесі теңдеулерді қанағаттандырады:
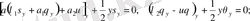 (2)
(2)
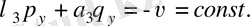 (3)
(3)
Екі фазалы сұйықтықты сүзгілеу екі ұңғыманың ортасынан өтеді деп алайық және олар мына нүктеде орналасқан
 Анығырақ айтсақ,
Анығырақ айтсақ,
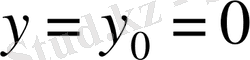 нүктесі мұнай айдау ұңғымасына, ал
нүктесі мұнай айдау ұңғымасына, ал
 - пайдаланып жатқан ұңғымаға сай келеді (
- пайдаланып жатқан ұңғымаға сай келеді (
 болуыда мүмкін) .
болуыда мүмкін) .
 ұңғымада не
ұңғымада не
 түрінде беріледі:
түрінде беріледі:
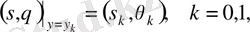 (4)
(4)
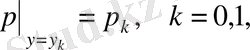 (5)
(5)
не мына өлшемдегі
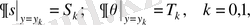 (6)
(6)
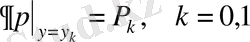 (7)
(7)
поток түрінде беріледі:
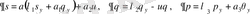 ,
,
мұндағы
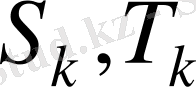 және
және
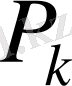 -тұрақтылар.
-тұрақтылар.
 және
және
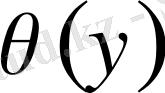 үшін (2), (4) бірінші шектік есепті шешеміз.
үшін (2), (4) бірінші шектік есепті шешеміз.
.
 коэффициентін белгілі функция деп алып,
коэффициентін белгілі функция деп алып,
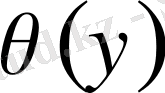 үшін келесі өрнектерге келеміз:
үшін келесі өрнектерге келеміз:
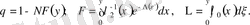 (8)
(8)
Мұндағы
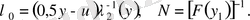
(8) өрнектен келесі бағалау орындалады:
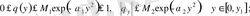 (9)
(9)
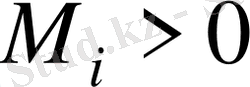 және
және
 тұрақтылары
тұрақтылары
 мәндеріне тәуелді емес.
мәндеріне тәуелді емес.
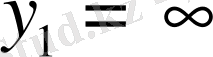 деп алып, (9) теңсіздіктегі
деп алып, (9) теңсіздіктегі
 мен
мен
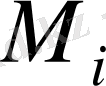 тұрақтыларын жуықтап есептейміз, сонда
тұрақтыларын жуықтап есептейміз, сонда
 болғандағы
болғандағы
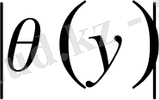 асимптотикасын анықтаймыз.
асимптотикасын анықтаймыз.
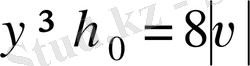 болсын, сонда
болсын, сонда
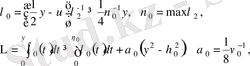
және ары қарай (9) теңсіздікте
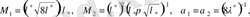
болғанда жеңіл орындалады. Мұндағы
 .
.
Енді
 үшін (2) теңдеуді қарастырамыз.
үшін (2) теңдеуді қарастырамыз.
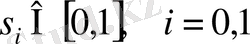 аралығына тәуелсіз (4) шарттағы
аралығына тәуелсіз (4) шарттағы
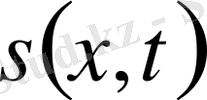 үшін мынадай бағалаулар белгілейміз
үшін мынадай бағалаулар белгілейміз
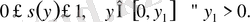 (10)
(10)
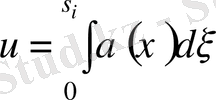 функциясын енгізейік және
функциясын енгізейік және
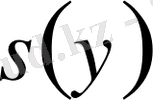 үшін (2) теңдеудің коэффициенттері белгілі деп алып, теңдеуді мына түрге келтіреміз
үшін (2) теңдеудің коэффициенттері белгілі деп алып, теңдеуді мына түрге келтіреміз
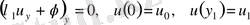 . (11)
. (11)
Мұндағы

(11) теңдеуді интегралдау арқылы мынаны аламыз
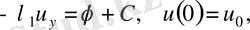 (12)
(12)
мұндағы
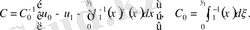 а
) -қасиетінен
а
) -қасиетінен
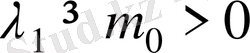 деп алсақ, онда (12) теңдеуден мына түрге келеміз
деп алсақ, онда (12) теңдеуден мына түрге келеміз
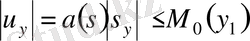 . (13)
. (13)
MLT-моделінің функционалдық параметрлерінің қасиеттеріне сәйкес теңсіздік орындалатынын байқаймыз:
в)
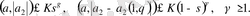
Теорема 1 (Тербелістің таралуының соңғы жылдамдығы туралы) .
а), б) және в) шарттары орындалсын, онда
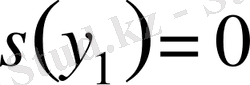 [немесе
[немесе
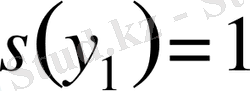 ],
],
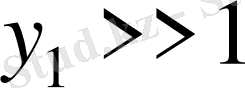 үшін
үшін
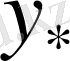 табылады.
табылады.
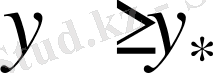 болғанда
болғанда
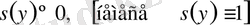 ,
(14)
,
(14)
яғни
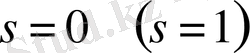 фронты соңғы жылдамдықпен таралады.
фронты соңғы жылдамдықпен таралады.
Дәлелдеу.
 (15)
(15)
деп алайық. Мұндағы
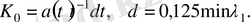
 және
және
 тұрақтылары
тұрақтылары
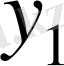 -ге тәуелді емес болғандықтан
-ге тәуелді емес болғандықтан
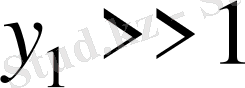 және
және
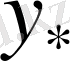 тұрақтысыда тәуелді емес.
тұрақтысыда тәуелді емес.
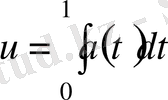 үшін (11) теңдеуді қарастырамыз.
үшін (11) теңдеуді қарастырамыз.
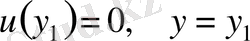 болғанда
болғанда
 деп алайық, онда
деп алайық, онда
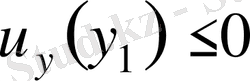 және
және
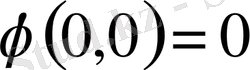 сияқты
сияқты
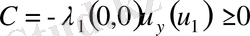 болады. Сонда
болады. Сонда
 болғанда
болғанда
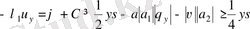 ,
,
Мұндағы
 (15) теңдікте анықталған. Осылайша мына теңсіздікке келеміз:
(15) теңдікте анықталған. Осылайша мына теңсіздікке келеміз:
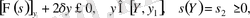 (16)
(16)
мұндағы
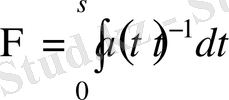 . Енді (16) теңсіздікті интегралдау арқылы
. Енді (16) теңсіздікті интегралдау арқылы
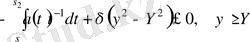 теңсіздігін аламыз.
теңсіздігін аламыз.
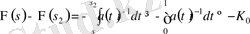 сияқты алдыңғы теңсіздікті
сияқты алдыңғы теңсіздікті
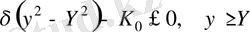 түрге келтіреміз, ал бұл
түрге келтіреміз, ал бұл
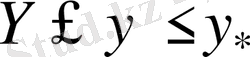 болғанда ғана орындалады. Демек, (16)
болғанда ғана орындалады. Демек, (16)
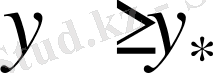 болғандағы дұрыстығын тексеру үшін (14) орындалуы қажет.
болғандағы дұрыстығын тексеру үшін (14) орындалуы қажет.
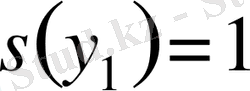 болғандағы жағдай
болғандағы жағдай
 орнына қарастырылады. Теорема дәлелденді.
орнына қарастырылады. Теорема дәлелденді.
(8), (12) өрнектерді
 вектор функциясы үшін Коши есебі түрінде жазамыз:
вектор функциясы үшін Коши есебі түрінде жазамыз:
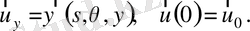 (17)
(17)
Мұндағы
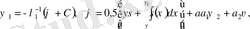
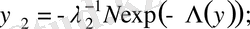
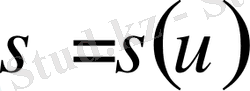 функциясы
функциясы
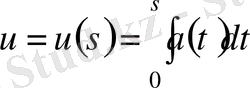 функциясына кері функция;
C
,
N
- тұрақтылар және
функциясына кері функция;
C
,
N
- тұрақтылар және
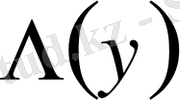 функциясы (8), (12) теңдіктерде анықталған. Кез келген
функциясы (8), (12) теңдіктерде анықталған. Кез келген
 үшін
а
),
б
) қасиеттері және
үшін
а
),
б
) қасиеттері және
 функциясы құрылымына қарай аргументтерінің жиынтығы үзіліссіз.
функциясы құрылымына қарай аргументтерінің жиынтығы үзіліссіз.
MLT-моделінің параметрлерінің қасиеттерінен в ) шартының келесі сәйкестігі шығады:
г
)
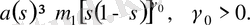
Теорема 2 (Гельдер үзіліссіздігі туралы) .
а), г) шарттары орындалсын делік, онда (17) есептегі
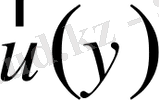 есептеу үшін априорлық бағалау орындалады. :
есептеу үшін априорлық бағалау орындалады. :
 (18)
(18)
Егер
 [немесе
[немесе
 ] болса, онда
] болса, онда
 тұрақтысы тек қана
тұрақтысы тек қана
 -ке тәуелді, барлық жағдайда
-ке тәуелді, барлық жағдайда
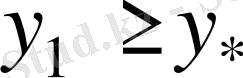 және жеке жағдайда
және жеке жағдайда
 деп алса болады.
деп алса болады.
Дәлелдеу.
Алдымен
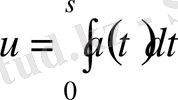 -ға кері Гельдердің үзіліссіздігімен өрнектейміз:
-ға кері Гельдердің үзіліссіздігімен өрнектейміз:
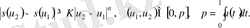
Ол үшін
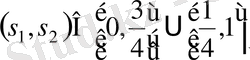 аралығында
аралығында
 орындалуы жеткілікті. Анықталуы үшін
орындалуы жеткілікті. Анықталуы үшін
 деп алсақта болады, сонда
деп алсақта болады, сонда
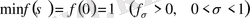 үшін теңсіздіктер тізбегінің ең соңғысы
үшін теңсіздіктер тізбегінің ең соңғысы
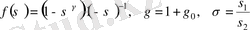 функциясын қарастырудан шығады.
функциясын қарастырудан шығады.
Сонымен
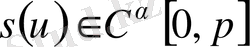 екені дәлелденді.
екені дәлелденді.
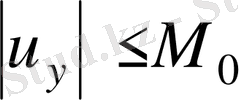 болса, онда
болса, онда
 болады. Енді (8), (12) теңдеулердің
болады. Енді (8), (12) теңдеулердің
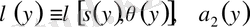 және басқа да Гельдер бойынша үзіліссіз коэффициенттері (18) -теңсіздік бойынша табылады.
және басқа да Гельдер бойынша үзіліссіз коэффициенттері (18) -теңсіздік бойынша табылады.
 және
және
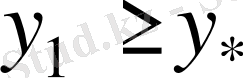 сияқты
сияқты
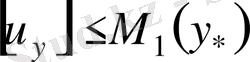 бағалауыда орындалады және де тербелістің таралуының соңғы жылдамдығына сәйкес
бағалауыда орындалады және де тербелістің таралуының соңғы жылдамдығына сәйкес
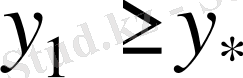 болғанда
болғанда
 болуы керек, онда теореманың тұжырымдарының дұрыстығына көз жеткіземіз.
болуы керек, онда теореманың тұжырымдарының дұрыстығына көз жеткіземіз.
Теорема 3.
а), г) шарттары орындалғанда барлық
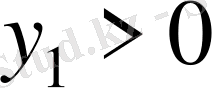 үшін (17) Коши есебінің бір ғана шешімі бар
үшін (17) Коши есебінің бір ғана шешімі бар
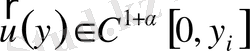 . Егер
. Егер
 болса, онда табылған шешімді
болса, онда табылған шешімді
 жалғастыруға болады.
жалғастыруға болады.
 болғанда
болғанда
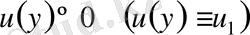 болады.
болады.
Дәлелдеу.
Теореманың бірінші бөлігі (18) бағалау және қасиеттері
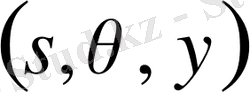 жай дифференциалдық теңдеулердің классикалық шешімдерінен дәлелденеді. Ал теореманың соңғы тұжырымдамасы 1, 2-теоремалардың салдары болып табылады. Теорема дәлелденді.
жай дифференциалдық теңдеулердің классикалық шешімдерінен дәлелденеді. Ал теореманың соңғы тұжырымдамасы 1, 2-теоремалардың салдары болып табылады. Теорема дәлелденді.
(2), (4) есептің жалпы шешімі деп
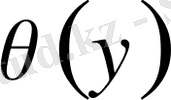 және
және
 функцияcын айтамыз, мұндағы
функцияcын айтамыз, мұндағы
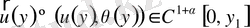 - (17) есептің шешімі, ал
- (17) есептің шешімі, ал
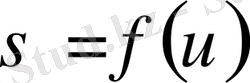 болса
болса
 функциясына кері функция. Мұндай жалпы шешім дәлелденген теоремадан шығады.
функциясына кері функция. Мұндай жалпы шешім дәлелденген теоремадан шығады.
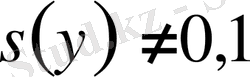 болғанда (2), (4) есептің
у
нүктесіндегі
болғанда (2), (4) есептің
у
нүктесіндегі
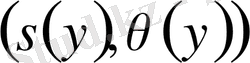 жалпы шешімі оның классикалық шешімі де болып табылады.
жалпы шешімі оның классикалық шешімі де болып табылады.
1. 4. Сандық зерттеу
Сандық эксперимент үш түрлі есепке жүргізілді:
I - бір бағыттағы сығымдау [(2), (4) есеп] ;
II - қысымды беогілі бір мөлшерде еөмендету - ұңғыманың әсер ету зонасы туралы есеп [(2), (5) есеп] ;
III - ағымға қарсы термокапилярлық сіңіру
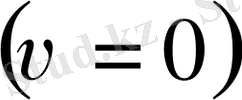 .
.
Әрбір жағдайдың өз ерекшелігі бар, бірақ есепті шығаруда жалпы сандық алгоритмдерін құрудың қиындықтары мынада:
-
 тәуелсіз айнымалының өзгеру аймағы шектеусіз;
тәуелсіз айнымалының өзгеру аймағы шектеусіз;
- теңдеулер жүйесі сызықты емес және туындылардың үлкен мәнінде матрица диоганальды емес;
- мұнайлы ортаның физикалық қасиеттеріне қарай
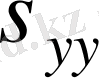 және
және
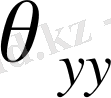 болғанда коэффициенттер өте аз, ал
болғанда коэффициенттер өте аз, ал
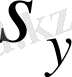 және
және
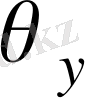 болғанда коэффициенттер таңбасын өзгертеді, яғни, шешімге тәуелді бұрылу нүктесі бар дегенді білдіреді. Демек, ішкі шекаралық қабаттардың пайда болғанын көрсетеді.
болғанда коэффициенттер таңбасын өзгертеді, яғни, шешімге тәуелді бұрылу нүктесі бар дегенді білдіреді. Демек, ішкі шекаралық қабаттардың пайда болғанын көрсетеді.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz