Шекаралық шарты болымсыз Штурм-Лиувилл операторының спектрлік қасиеттері


МАЗМҰНЫ
КІРІСПЕ . . 8
I Тарау
- Түрлендіру операторлары . . . 15
- Кесіндідегі Штурм-Лиувиллдің шекаралық есептері . . . 18
- Кеңістік туралы түсінік . . . 21
II Тарау
2. Штурм-Лиувиллдің болымсыз операторы . . . 36
2. 1. Алғашқы мәліметтер . . . 42
2. 2. Штурм-Лиувиллдің болымсыз операторының шекаралық шартын қорытып шығару . . . 42
- Сыңар операторды тұрғызу . . . 45
- Болымсыз Штурм-Лиувилл операторының спектрінің
табиғаты . . . 46
- Шекаралық шарты болымсыз Штурм-Лиувилл операторының волтерлі болуының үзілді-кесілді шарты . . . 49
- Шекаралық шарты болымсыз Штурм-Лиувилл есебінің шешімсіздігінің үзілді-кесілді шарты . . . 52
III Тарау
3. 1 Шекаралық шарты болымсыз, Штурм-Лиувилл операторының
спектрінің шексіз көп екендігі туралы . . . 53
3. 2 Шекаралық шарты болымсыз Штурм-Лиувилл операторының
меншікті функциясының нормасы . . . 56
3. 3 Спектрдің шекаралық шартқа тәуелділігі туралы . . . 56
3. 4 Моделді оператор жағдайы . . . 60
Қорытынды . . . 67
Қолданылған әдебиеттер тізімі . . . 68
АННОТАЦИЯ
В настоящей дипломной работе изучены спектральные свойства оператора Штурма-Лиувилля с вырожденным краевым условием. Полученные результаты носят предварительный характер.
АННОТАЦИЯ
Бұл еңбекте шекаралық шарты болымсыз Штурма-Лиувилл операторының спектрәлдік қасиеттері зерттелген. Алынған нәтижелер түпкілікті емес, әлі де зерттей түсуді қажет етеді.
Abstract
In the present degree job the spectral properties of the operator of Storm - Lyuvill with by a regional condition are investigated. The received results carry preliminary character.
КІРІСПЕ
Штурм-Лиувилл операторлары шамамен 1830 жылдан бастап зерттеле бастады десек-те дәл осы күнге дейін өзінің толық шешімін таба қойған жоқ. Көптеген мәселелердің түйіндері тарқатыла қойған жоқ, солардың бірі болымсыз Штурм-Лиувилл операторының спектрәлдік қасиеттері, яғни шекаралық шарттары мына
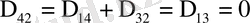 (0. 1)
(0. 1)
теңдіктерді қанағаттандыратын мынадай
, (0. 2)
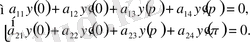 (0. 3)
(0. 3)
Штурм-Лиувилл операторлары, мұндағы
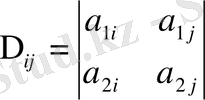 ,
,
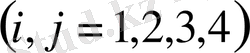 , (0. 4)
, (0. 4)
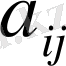 -Штурм-Лиувилл операторының шекаралық шартының коэффициенті. Соңғы уақытқа дейін бұл оператордың спектрәлдік қасиеттері туралы ешнәрсе белгісіз еді. Өткен XX-ғасырдың басында пайда болған Биркгофтың теориясына бұл оператор енбей қалған және бұл кездейсоқ жай емес. Қысқаша айтсақ мұндай операторлардың спектрәлдік қасиеттері q(x) коэффициентіне өте тәуелді, ал Биркгоф қарастырған жағдайда бұлай емес еді. Біздің бұл есепке тісіміз бата қоймады, сондықтан тек кейбір дербес жағдайларды қарастырумен шектелдік.
-Штурм-Лиувилл операторының шекаралық шартының коэффициенті. Соңғы уақытқа дейін бұл оператордың спектрәлдік қасиеттері туралы ешнәрсе белгісіз еді. Өткен XX-ғасырдың басында пайда болған Биркгофтың теориясына бұл оператор енбей қалған және бұл кездейсоқ жай емес. Қысқаша айтсақ мұндай операторлардың спектрәлдік қасиеттері q(x) коэффициентіне өте тәуелді, ал Биркгоф қарастырған жағдайда бұлай емес еді. Біздің бұл есепке тісіміз бата қоймады, сондықтан тек кейбір дербес жағдайларды қарастырумен шектелдік.
Бұл дипломдық жұмыс екі бөлімнен, кіріспеден қорытындыдан және іс барысында қолданылған әдебиеттер тізімінен тұрады. Бірінші бөлім көмекші қызмет атқарады, барлық негізгі нәтижелер екінші бөлімде келтірілді. Бірінші бөлімде, кейінірек қолданылатын барлық анықтамалар мен негізгі ұғымдар келтірілді.
Екінші бөлімнің бірінші бөлімшесінде Штурм-Лиувиллдің операторлар теориясының негізгі анықтамалары мен қарапайым деректері хабарланды, сонан соң мәселенің мәні айқындалды.
МӘСЕЛЕНІҢ МӘНІ. Егер
(0. 1)
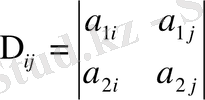 ,
,
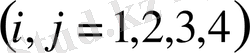 , (0. 2)
, (0. 2)
болса, онда мына
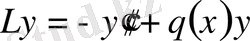 , (0. 3)
, (0. 3)
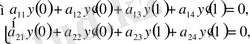 (0. 4)
(0. 4)
Штурм-Лиувилл операторының спектрәлдік қасиеттері қандай?
Дәл осы бөлімшеде, кейінірек көп қолданылатын, қарапайым ғана лемма дәлелденді.
ЛЕММА 1. 3. Анықтауыш
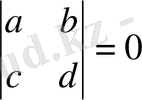 ,
,
болсын делік, онда егер
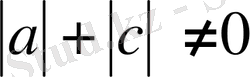 болса, онда
болса, онда
 және
және
 немесе басқаша айтсақ
немесе басқаша айтсақ
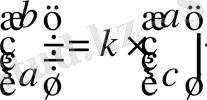 (0. 5)
(0. 5)
мұндағы
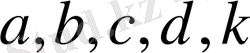 - комплекс сандар.
- комплекс сандар.
Осы лемма арқылы келесі 1. 4 леммасы дәлелденді, ол біздің шекаралық есеп пен спектрі жоқ Коши есебі арасында байланыс бар екенін нақты көрсетіп берді. Жалпы айтқанда спектрі жоқ есептерді волтерлік есептер деп атайды.
ЛЕММА 1. 4. Егер (4) шекаралық шарттар өзара сызықтық тәуелсіз болса және
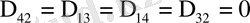 , (0. 6)
, (0. 6)
теңдіктері орындалса, онда бұл шекаралық есеп Кошидің есебі болады.
Екінші бөлімшеде болымсыз оператордың шекаралық шарты мұқият зерттеліп, нәтижесінде 2. 1 лемма мен 2. 1 теоремасы дәлелденді.
ЛЕММА 2. 1. Егер мына
1)
 ; 2)
; 2)
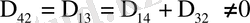 , (0. 7)
, (0. 7)
теңсіздіктер орындалса, онда (0. 4) шекаралық шарты мынадай
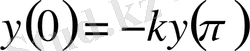 ,
,
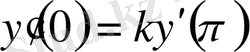 , (0. 8)
, (0. 8)
шекаралық шартпен бірдей болады, мұндағы
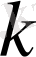 - белгілі бір комплекс сан.
- белгілі бір комплекс сан.
ТЕОРЕМА 2. 1. Егер
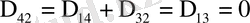 , (0. 9)
, (0. 9)
болса, онда комплекс
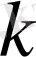 саны табылып
саны табылып
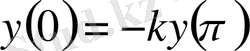 ,
,
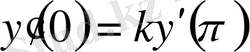 . (0. 10)
. (0. 10)
теңдіктері орындалады, яғни басқаша айтсақ болымсыз шекаралық шарт осындай шартқа айналады.
Үшінші бөлімшеде болымсыз Штурм-Лиувилл операторының сыңары тұрғызылды.
Төртінші бөлімшеде шекаралық шарты болымсыз Штурм-Лиувилл операторының спектрәлдік қасиеттері зерттелді, нәтижесінде екі лемма және екі теорема дәлелденді. Олар мыналар:
ЛЕММА 4. 1.
Егер
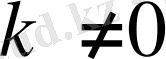 болса, онда
болса, онда
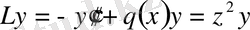 , (0. 11)
, (0. 11)
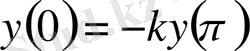 ,
,
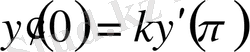 (0. 12)
(0. 12)
Штурм-Лиувилл операторының характеристикалық анықтауышы мына
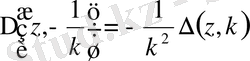 . (0. 13)
. (0. 13)
қанағаттандырады.
ЛЕММА 4. 2.
Егер
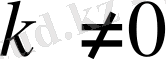 және
және
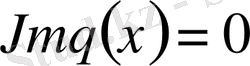 болса, онда сыңар оператордың меншікті мәндері мына
болса, онда сыңар оператордың меншікті мәндері мына
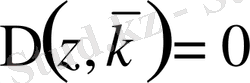 . (0. 14)
. (0. 14)
теңдеуінің түбірлері болады.
ТЕОРЕМА 4. 1.
(а) егер Штурм-Лиувиллдің шекаралық есебі болымсыз болса, онда ол мынадай
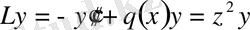 , (0. 15)
, (0. 15)
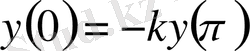 ,
,
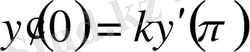 (0. 16)
(0. 16)
болады, мұндағы
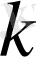 -бірлік дөңгелекте орналасқан комплекс сан.
-бірлік дөңгелекте орналасқан комплекс сан.
(б)
Егер Штурм-Лиувиллдің болымсыз операторының
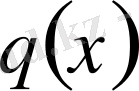 коэффициенті нақты функция болса, онда ол (15) +(16) түрінде болады, тек
коэффициенті нақты функция болса, онда ол (15) +(16) түрінде болады, тек
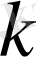 параметрі жоғарғы жарты дөңгелекте болады, ал төменгі жарты дөңгелектегі
параметрі жоғарғы жарты дөңгелекте болады, ал төменгі жарты дөңгелектегі
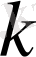 -лар сыңар операторды анықтайды.
-лар сыңар операторды анықтайды.
ТЕОРЕМА 4. 2.
Егер
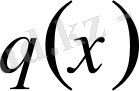 нақты функция, ал
нақты функция, ал
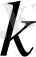
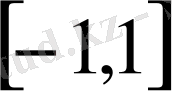 кесіндісінің нөлден өзгеше саны болса, онда (15) +(16) операторы мен оның сыңарының спектрлері бірдей болады.
кесіндісінің нөлден өзгеше саны болса, онда (15) +(16) операторы мен оның сыңарының спектрлері бірдей болады.
САЛДАР 4. 2.
Егер
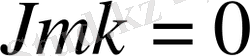 және
және
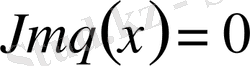 болса, онда (15) +(16) есептің спектрі
болса, онда (15) +(16) есептің спектрі
 осіне қарағанда симметриялы болады.
осіне қарағанда симметриялы болады.
Бесінші бөлімшеде бір 5. 1 қорытынды леммасы дәлелденген, кейінірек олар кеңінен қолданылады.
ЛЕММА 5. 1.
Егер экспонента сияқты
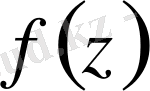 функциясының бүкіл комплекс жазықтықта нөлдері жоқ болса, онда
функциясының бүкіл комплекс жазықтықта нөлдері жоқ болса, онда
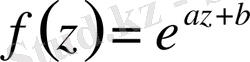 (0. 17)
(0. 17)
теңдігі орындалады, мұндағы
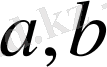 -белгілі комплекс сандар.
-белгілі комплекс сандар.
САЛДАР 5. 1.
Егер экспонента сияқты жұп
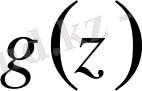 функциясының нөлдері жоқ болса, онда ол нөлден өзгеше тұрақты шама.
функциясының нөлдері жоқ болса, онда ол нөлден өзгеше тұрақты шама.
Мына
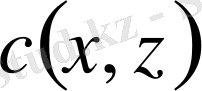 ,
,
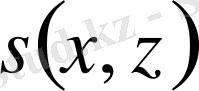 функциялары
функциялары
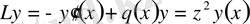 , (0. 18)
, (0. 18)
теңдеуінің мына
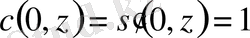 ,
,
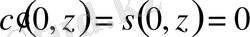 . (0. 19)
. (0. 19)
шарттарды қанағаттандыратын шешімдерінің фундаментәлді жүйесі болсын. Онда келесі лемма орындалады.
ЛЕММА 5. 2. Егер
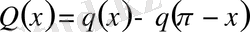
болса, онда мынадай
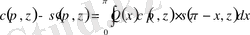 , (0. 20)
, (0. 20)
теңдік орындалады.
Боргтың келесі леммасы да болымсыз Штурм-Лиувилл операторының спектрәлдік қасиеттерін зерттегенде маңызды қызмет атқарады.
ЛЕММА 5. 3.
Егер
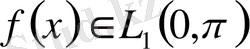 және
және
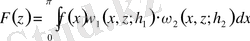 , (0. 21)
, (0. 21)
ал
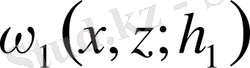 мен
мен
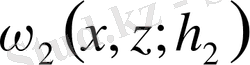 функциялары коэффициенттері сәйкесінше
функциялары коэффициенттері сәйкесінше
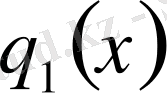 ,
,
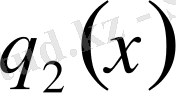 болатын Штурм-Лиувилл теңдеулерінің шешімі болса, онда
болатын Штурм-Лиувилл теңдеулерінің шешімі болса, онда
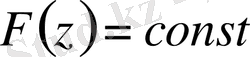 (0. 22)
(0. 22)
теңдігі
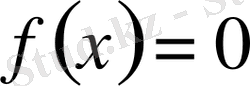 болғанда ғана орындалады. Бұл бөлімшенің негізгі нәтижесі мына теорема.
болғанда ғана орындалады. Бұл бөлімшенің негізгі нәтижесі мына теорема.
ТЕОРЕМА 5. 1. Жоғарыдағы (0. 15) +(0. 16) операторының спектрі жоқ болуы үшін
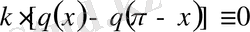 ,
,
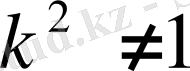 . (0. 23)
. (0. 23)
шарттары орындалуы қажетті әрі жеткілікті.
Келесі алтыншы бөлімшеде болымсыз Штурм-Лиувилл операторының тағы да бір ерекше қасиеті зерттелді.
Алынған нәтиженің мән-мағынасы теореманың тұжырымынан көрініп тұр.
ТЕОРЕМА 6. 1. Мына
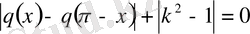 . (0. 24)
. (0. 24)
теңдік орындалған жағдайда және тек осы жағдайда ғана (0. 15) +(0. 16) оператордың спектрі бүкіл комплекс z жазықтығы болады.
Зерттеу барысында жаңа ұғым пайда болды, біз оны келесі анықтама ретінде тұжырымдадық.
АНЫҚТАМА 7. 1 Спектрі жоқ немесе бүкіл комплекс жазықтық болатын Штурм-Лиувилл операторын Штурм-Лиувиллдің болымсыз операторы деп атаймыз.
Келесі теорема Штурм-Лиувилл операторының болымсыз болуының үзілді-кесілді шартын анықтайды.
ТЕОРЕМА 7. 1. Мына
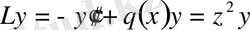 , (0. 25)
, (0. 25)
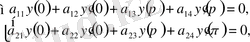 (0. 26)
(0. 26)
Штурм-Лиувилл операторы болымсыз болуы үшін мына,
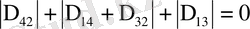 , (0. 27)
, (0. 27)
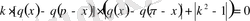 , (0. 28)
, (0. 28)
шарттардың орындалуы қажетті әрі жеткілікті, мұндағы
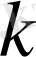 -жоғарыдағы (0. 16) шекаралық шарттың тұрақтысы, ал q(x) -комплекс мәнді үздіксіз функция.
-жоғарыдағы (0. 16) шекаралық шарттың тұрақтысы, ал q(x) -комплекс мәнді үздіксіз функция.
Сегізінші бөлімшеде 8. 1 леммасы мен 8. 1 теоремасы дәлелденді. Енді соларға тоқталайық.
ЛЕММА 8. 1.
Егер (0. 15) +(0. 16) Штурм-Лиувилл операторының
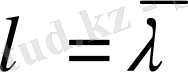 нақты меншікті мәні бар болса, онда
нақты меншікті мәні бар болса, онда
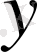 ,
,
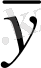 функциялары бір Штурм-Лиувилл теңдеуінің сызықтық тәуелді шешімдері болады. Мұндағы
функциялары бір Штурм-Лиувилл теңдеуінің сызықтық тәуелді шешімдері болады. Мұндағы
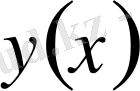 дегеніміз
дегеніміз
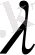 меншікті мәніне сәйкес меншікті функция.
меншікті мәніне сәйкес меншікті функция.
ТЕОРЕМА 8. 1.
Егер (0. 15) +(0. 16) операторының кемінде бір нақты
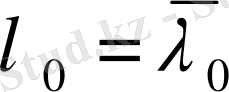 меншікті мәні бар болса, онда
меншікті мәні бар болса, онда
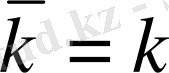 .
.
Тоғызыншы бөлімшеде шекаралық шарты болымсыз операторының спектрінің шекаралық шартқа тәуелділігі зерттелді, нәтижесінде 9. 1, 9. 2 леммалар мен 9. 1 теоремасы алынды. Олар мыналар:
ЛЕММА 9. 1. Егер мына
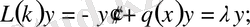
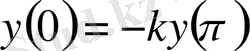 ,
,
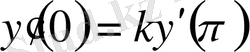 , (0. 29)
, (0. 29)

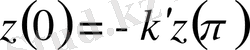 ,
,
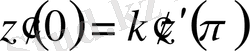 , (0. 30)
, (0. 30)
Екі операторға ортақ
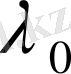 деген меншікті мән бар болса, онда
деген меншікті мән бар болса, онда
а)
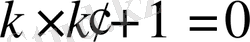 ; немесе
; немесе
б) осы меншікті мәнге сәйкес екі меншікті функция өзара сызықты тәуелді.
ЛЕММА 9. 2.
Егер
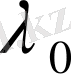 жоғарыдағы (0. 29), (0, 30) операторларына ортақ меншікті мән болса, онда
жоғарыдағы (0. 29), (0, 30) операторларына ортақ меншікті мән болса, онда
а)
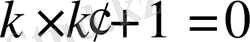 ; немесе (0. 31)
; немесе (0. 31)
б)
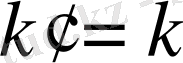 . (0. 32)
. (0. 32)
ТЕОРЕМА 9. 1.
Егер
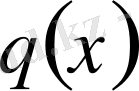 - үзіліссіз нақты функция, ал
- үзіліссіз нақты функция, ал
 болса, онда мына
болса, онда мына
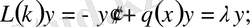
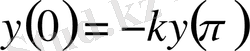 ,
,
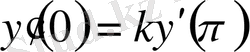 (0. 33)
(0. 33)
операторлардың әртүрлі
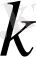 -лар сәйкес спектрлері мүлдем әртүрлі болады, яғни спектрлердің жиын ретінде ортақ мүшелері болмайды.
-лар сәйкес спектрлері мүлдем әртүрлі болады, яғни спектрлердің жиын ретінде ортақ мүшелері болмайды.
Оныншы бөлімшеде зерттелген оператордың ең қарапайым үлгісі қарастырылды, және сол арқылы бұрынғы нәтижелер тексерілді.
ТЕОРЕМА 10. 1.
Егер
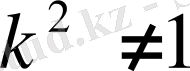 болса, онда то
болса, онда то
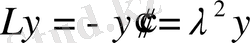 ,
,
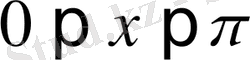 (0. 34)
(0. 34)
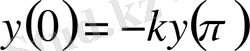 ,
,
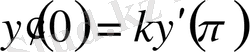 (0. 35)
(0. 35)
шекаралық есебінің нөлден өзгеше шешімі жоқ, яғни Кошидің есебі сияқты.
ТЕОРЕМА 10. 2.
Егер
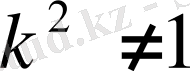 , ал
, ал
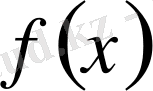 функциясы
функциясы
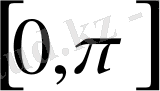 сегментінде үзіліссіз болса, онда мына
сегментінде үзіліссіз болса, онда мына
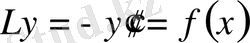 ,
,
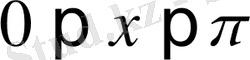 (0. 36)
(0. 36)
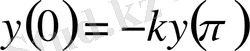 ,
,
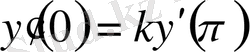 , (0. 37)
, (0. 37)
шекаралық есептің бірегей шешімі бар және ол мынадай,
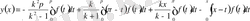 . (0. 38)
. (0. 38)
- 1. 1. Түрлендіру операторы
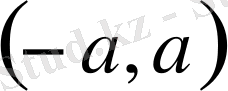
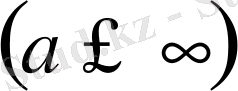 интервалында Штурм-Лиувиллдің дифференциалдық теңдеуін қарастырайық:
интервалында Штурм-Лиувиллдің дифференциалдық теңдеуін қарастырайық:
(1. 1)
мұндағы
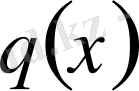 - осы интервалдағы үзіліссіз комплексті функция, ал
- осы интервалдағы үзіліссіз комплексті функция, ал
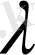 -комплексті параметр. Кейінірек
-комплексті параметр. Кейінірек
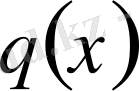 функциясын бұл теңдеудің потенциалы немесе
функциясын бұл теңдеудің потенциалы немесе
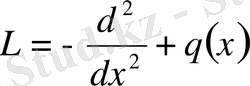 Штурм-Лиувилл операторына сәйкес келетін функция деп атаймыз. Бастапқы берілген (1) теңдеудің шешімін
Штурм-Лиувилл операторына сәйкес келетін функция деп атаймыз. Бастапқы берілген (1) теңдеудің шешімін
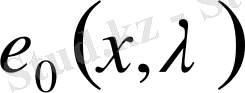 арқылы белгілейік.
арқылы белгілейік.
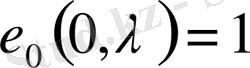 ,
,
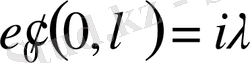 (1. 2)
(1. 2)
(здесь индекс «0» означает, что начальные данные задаются в точке 0, а буква
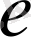 напоминает, что они такие же, как у функции
напоминает, что они такие же, как у функции
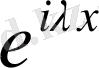 , с которой совпадает
, с которой совпадает
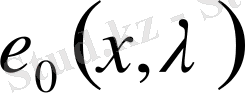 , если
, если
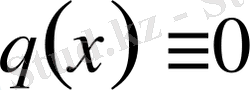 ) .
) .
ТЕОРЕМА 1. 1. (2)
бастапқы берілген (1) теңдеудің шешімі
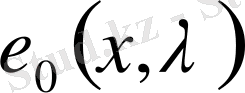 мына түрде болады:
мына түрде болады:
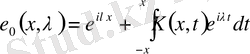 , (1. 3)
, (1. 3)
Мұндағы
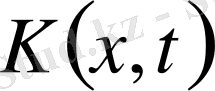 - үзіліссіз функция, Римана функциясы арқылы өрнектелген теңдеу мынадай
- үзіліссіз функция, Римана функциясы арқылы өрнектелген теңдеу мынадай
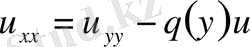
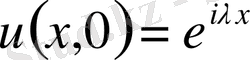 ,
,
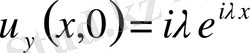
мына формуладан
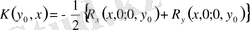 .
.
Интегралдық оператор
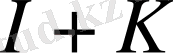 мына формула арқылы анықталған
мына формула арқылы анықталған
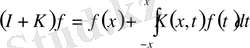 ,
,
түрлендіру операторы деп атаймыз,
 нүктесінде бастапқы шарт сақталынған. Ол мынадай
нүктесінде бастапқы шарт сақталынған. Ол мынадай
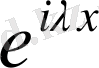 функцияны ( (2) бастапқы берілген қарапайым теңдеу (1) түрінің шешімі ) сол сияқты бастапқы берілген (1) теңдеудің шешіміне көшіреді.
функцияны ( (2) бастапқы берілген қарапайым теңдеу (1) түрінің шешімі ) сол сияқты бастапқы берілген (1) теңдеудің шешіміне көшіреді.
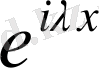 және
және
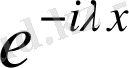 функциялары
функциялары
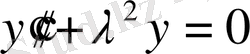 теңдеуінің шешімінің фундаментальді жүйесін құрастырады. Бастапқы берілген 0-нүктесінде (1) теңдеудің шешімін
теңдеуінің шешімінің фундаментальді жүйесін құрастырады. Бастапқы берілген 0-нүктесінде (1) теңдеудің шешімін
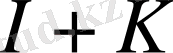 операторы бұл теңдеудің кез келген шешіміне түрлендіреді. Сондықтан бастапқы берілген (1) теңдеуінің шешімі
операторы бұл теңдеудің кез келген шешіміне түрлендіреді. Сондықтан бастапқы берілген (1) теңдеуінің шешімі
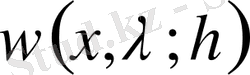
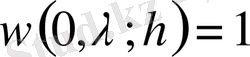 Equation. 3,
Equation. 3,
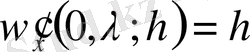 (1. 4)
(1. 4)
Мына түрде қарастырсақ:
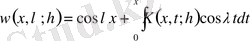 , (1. 5)
, (1. 5)
мұндағы
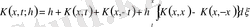 . (1. 6)
. (1. 6)
Бастапқы берілген (1) теңдеудің аналитикалық
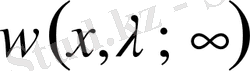 шешімі
шешімі
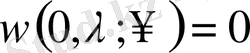 Equation. 3,
Equation. 3,
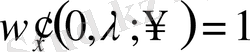 (1. 7)
(1. 7)
Мына түрде беруге болады
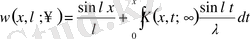 , (1. 8)
, (1. 8)
мұндағы
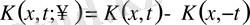 . (1. 9)
. (1. 9)
Осы 1. 1. теоремасынан мынадай салдар шығады.
САЛДАР 1. 1. (4), (7) бастапқы берілгендер үшін (1) теңдеудің шешімін мына түрде жазуға болады
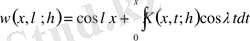 , (1. 10)
, (1. 10)
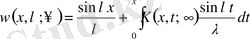 , (1. 11)
, (1. 11)
мұндағы
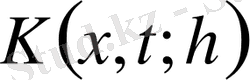 функция,
функция,
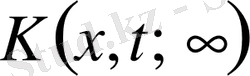 функциясы (6), (9) формуласындағы (3) операторының
функциясы (6), (9) формуласындағы (3) операторының
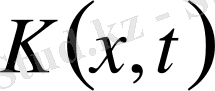 ядросы бойынша өрнектеледі.
ядросы бойынша өрнектеледі.
(3), (10), (11) теңдігінің оң жағында анықталған
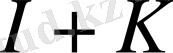 ,
,
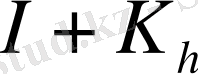 ,
,
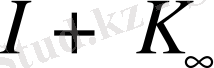 , операторын 0 нүктесіне байланған түрлендіру операторы деп атаймыз.
, операторын 0 нүктесіне байланған түрлендіру операторы деп атаймыз.
ЛЕММА 1. 1.
Егер (2) бастапқы берілгендер үшін (1) теңдеудің
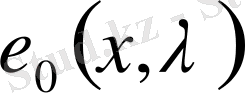 шешімі барлық
шешімі барлық
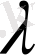 мәнінде (3) формуламен берілсе, онда
мәнінде (3) формуламен берілсе, онда
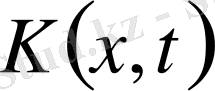 ядросы мына теңдеуді қанағаттандырады
ядросы мына теңдеуді қанағаттандырады
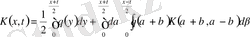 (1. 12)
(1. 12)
және, керісінше, егер
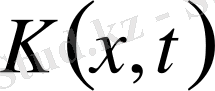 функциясы (12) теңдеуін қанағаттандырса, онда (3) формуласы оң жағындағы барлық
функциясы (12) теңдеуін қанағаттандырса, онда (3) формуласы оң жағындағы барлық
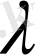 мәндерінде үшін (2) бастапқы берілгендер үшін (1) теңдеудің
мәндерінде үшін (2) бастапқы берілгендер үшін (1) теңдеудің
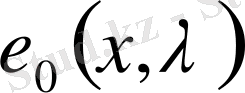 шешімі болады.
шешімі болады.
ТЕОРЕМА 1. 2. (12) теңдеудің жалғыз ғана шешімі бар. Бұл шешім үзіліссіз және мына теңсіздікті қанағаттандырады
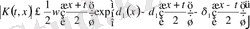 , (1. 13)
, (1. 13)
мұндағы
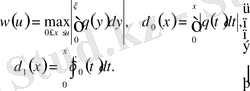 (1. 14)
(1. 14)
Егер
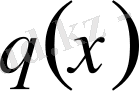 функциясы
функциясы
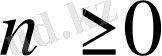 үзіліссіз туындысы болса, онда
үзіліссіз туындысы болса, онда
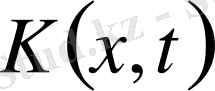 ядросының
ядросының
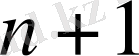 екі жақты алмастыру бойынша үзіліссіз туындысы бар.
екі жақты алмастыру бойынша үзіліссіз туындысы бар.
САЛДАР 1. 2.
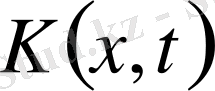 функциясы (3) түрлендіру операторының ядросы болу үшін
функциясы (3) түрлендіру операторының ядросы болу үшін
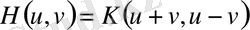 функциясы Гурс есебінің шешімі болуы қажетті және жеткілікті:
функциясы Гурс есебінің шешімі болуы қажетті және жеткілікті:
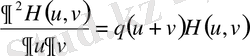 ,
,
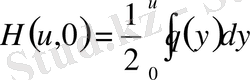 ,
,
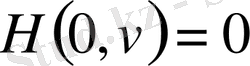 . (1. 15)
. (1. 15)
Егер
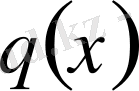 функциясы үзіліссіз дифференциалданса, онда (1. 15) есебі былай түрленеді:
функциясы үзіліссіз дифференциалданса, онда (1. 15) есебі былай түрленеді:
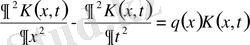 ,
,
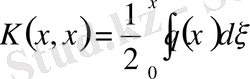 ,
,
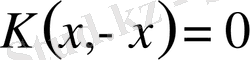 . (1. 16)
. (1. 16)
- Ақырғы интервалдағы Штурма-Лиувиллдің шекаралық есебі
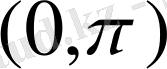 аралығында Штурма-Лиувилл теңдеунің шекаралық есебін қарастырайық:
аралығында Штурма-Лиувилл теңдеунің шекаралық есебін қарастырайық:
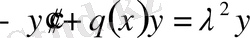 , (2. 1)
, (2. 1)
және екі шекаралық шарттармен
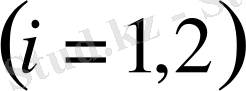 :
:
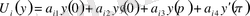 , (2. 2)
, (2. 2)
мұндағы
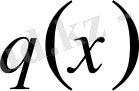 - қосатын комплексмәнді функция,
- қосатын комплексмәнді функция,
 - туындылы комплексті сандар.
- туындылы комплексті сандар.
Параметрмәні
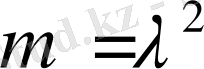 болғанда, мұндай шекаралық есептердің нөлдік шешімдері болса, онда оны меншікті мән деп атаймыз, ал оған сәйкес шешім- меншікті функция деп аталады. (1) теңдеуінің фундаментальді жүйесінің шешімі мына анықталған бастапқы берілгендерді
болғанда, мұндай шекаралық есептердің нөлдік шешімдері болса, онда оны меншікті мән деп атаймыз, ал оған сәйкес шешім- меншікті функция деп аталады. (1) теңдеуінің фундаментальді жүйесінің шешімі мына анықталған бастапқы берілгендерді
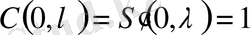 ,
,
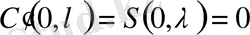 мынау
мынау
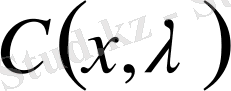 ,
,
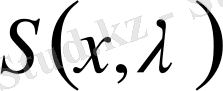 арқылы белгілейік ( сонымен
арқылы белгілейік ( сонымен
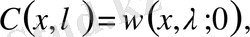
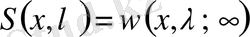 алдынғы бөлімшеде белгіленген ) . Сондықтан (1) теңдеуінің
алдынғы бөлімшеде белгіленген ) . Сондықтан (1) теңдеуінің
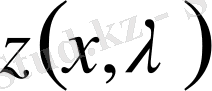 жалпы шешімі
жалпы шешімі
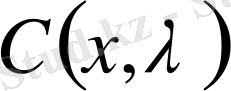 ,
,
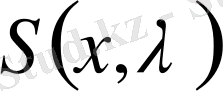 :
:
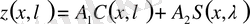 функциясының сызықты комбинациясы болса, онда
функциясының сызықты комбинациясы болса, онда
 , (2. 3)
, (2. 3)
бұдан, (1), (2) шекаралық есептің нөлдік шешімі болады сонда ғана, егер теңдеулер жүйесі
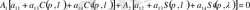 ,
,
 ,
,
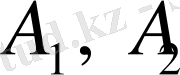 коэффициенттерінің нөлдік шешімі болса. Сондықтан меншікті мән қарастырылған есепке квадрат түбірмен оның характеристикалық функциясы сәйкес келеді.
коэффициенттерінің нөлдік шешімі болса. Сондықтан меншікті мән қарастырылған есепке квадрат түбірмен оның характеристикалық функциясы сәйкес келеді.
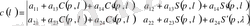 . (2. 4)
. (2. 4)
Мына анықтауышты ескере отырып вронскиан
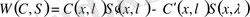 бірге тең болатындығын көреміз, сол арқылы
бірге тең болатындығын көреміз, сол арқылы
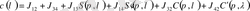 , (2. 4
/
)
, (2. 4
/
)
Функциясын табамыз. Мұндағы
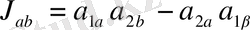 -анықтауыш, шекаралық шарттың коэффициенті
-анықтауыш, шекаралық шарттың коэффициенті
 ,
,
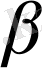 матрица бағандарынан құралған.
матрица бағандарынан құралған.
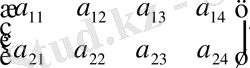 .
.
Бұдан
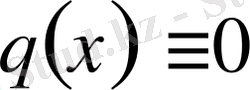 болғанда, (1) -(2) шекаралық есептің
болғанда, (1) -(2) шекаралық есептің
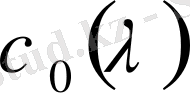 характеристикалық функциясы мына түрге келеді:
характеристикалық функциясы мына түрге келеді:
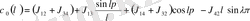 (2. 6)
(2. 6)
және қарапайым жағдайда, яғни
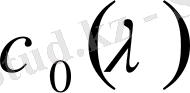 функцисы нөлден өзгеше болғанда меншікті жүйенің толықтығы және тек шекаралық шарттарға қоюға болатын қосарланған функция туралы сұрақ туады. Бұл келесі 3 шарттың орындалу мүмкіндігін көрсетеді:
функцисы нөлден өзгеше болғанда меншікті жүйенің толықтығы және тек шекаралық шарттарға қоюға болатын қосарланған функция туралы сұрақ туады. Бұл келесі 3 шарттың орындалу мүмкіндігін көрсетеді:
1)
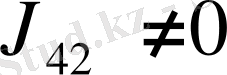 ;
2)
;
2)
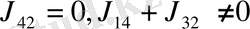 ;
3)
;
3)
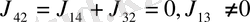 . (2. 7)
. (2. 7)
Шекаралық шарт бұлардың кемінде біреуін қанағаттандырса, онда ол болымды деп аталады.
ТЕОРЕМА 2. 1.
(1) -(2) толық болымды шекаралық шарттармен берілген меншікті жүйе және қосарланған функцияның шекаралық есебін
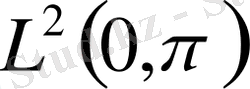 кеңістігінде қарастырған.
кеңістігінде қарастырған.
Қосарланған функция анықтамасын еске түсірейік.
(4) анықтауышын
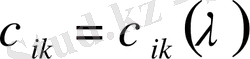 элементі арқылы белгілеп, (1) теңдеуінің шешімін құрастырайық:
элементі арқылы белгілеп, (1) теңдеуінің шешімін құрастырайық:
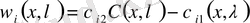 . (2. 8)
. (2. 8)
(3) формуласынан тура
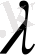 -ға тең екендігін көреміз.
-ға тең екендігін көреміз.
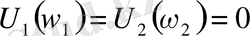 ,
,
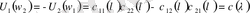 .
.
(1) -(2) шекаралық есептің
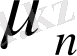 меншікті мәні
меншікті мәні
 - еселік деп аталады, егер
- еселік деп аталады, егер
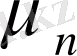
 функциясының
функциясының
 еселік түбірі болса.
еселік түбірі болса.
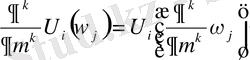 ,
,
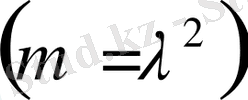 ,
,
болса, онда функция
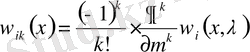 ,
,
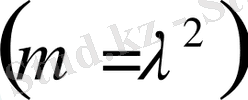
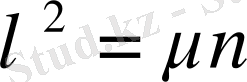 - (2) шекаралық шартын қанағаттандырады, егер
- (2) шекаралық шартын қанағаттандырады, егер
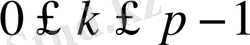 болса.
болса.
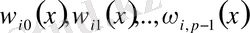
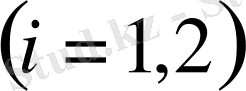 функциялары тізбек құралады, біріншісі нөлден өзгеше
функциялары тізбек құралады, біріншісі нөлден өзгеше
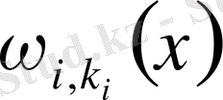 функциясы меншікті болады, ал келесілері функцияларға қосарланған. (1) теңдеуін
функциясы меншікті болады, ал келесілері функцияларға қосарланған. (1) теңдеуін
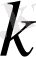 рет
рет
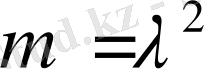 бойынша дифференциалдай отырып, (2) шекаралық шартын және
бойынша дифференциалдай отырып, (2) шекаралық шартын және
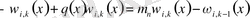 теңдеуін қанағаттандыратын меншікті және қосарланған функциялар тізбегін қорытып шығарайық.
теңдеуін қанағаттандыратын меншікті және қосарланған функциялар тізбегін қорытып шығарайық.
Бөліктелген шекаралық шарттармен берілген
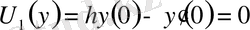 ,
,
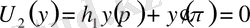 (2. 9)
(2. 9)
шекаралық есептерді қарастыра отырып
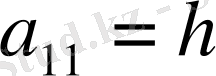 ,
,
 ,
,
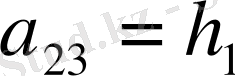 ,
,
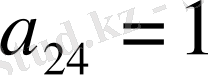 ,
,
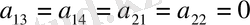 . (2. 9
/
)
. (2. 9
/
)
аламыз. Бұдан
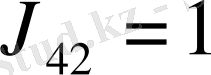 болған жағдайда шекаралық шарт болымды, ал меншікті жүйе және қосарланған функция толығымен
болған жағдайда шекаралық шарт болымды, ал меншікті жүйе және қосарланған функция толығымен
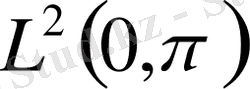 кеңістігінде жатады.
кеңістігінде жатады.
Шындығында, меншікті және қосарланған функциялардың (1), (9) шекаралық шарттары
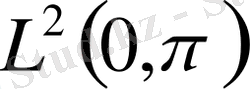 кеңістігінде базис құрады. .
кеңістігінде базис құрады. .
1. 3. 1. Нормаланған кеңістік.
Функцианалдық тандаудағы көбінесе кездесетін жалпы кеңістіктер сызықтық (векторлық) топологиялық кеңістік, яғни
C
комплекс сандар өрісінің (немесе
R
нақты сандарының )
 сызықтық кеңістік болып табылады. Бұл кеңістік бір мезгілде топологиялық және сызықты операциялар осы кеңістікте үзіліссіз. Дербес, бірақ өте қажетті жағдай,
сызықтық кеңістік болып табылады. Бұл кеңістік бір мезгілде топологиялық және сызықты операциялар осы кеңістікте үзіліссіз. Дербес, бірақ өте қажетті жағдай,
 сызықтық кеңістігінде қасиеттері қарапайым евклидтік кеңістігінің векторлар ұзындығының қасиеттерінің жалпыламасы болатындай векторлар нормасын (ұзындығын) сиғызуға болады. Дәл
сызықтық кеңістігінде қасиеттері қарапайым евклидтік кеңістігінің векторлар ұзындығының қасиеттерінің жалпыламасы болатындай векторлар нормасын (ұзындығын) сиғызуға болады. Дәл
 элементінің нормасы деп,
элементінің нормасы деп,
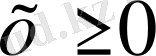 және
және
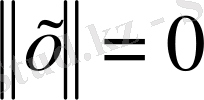 тек қана
тек қана
 болған жағдайда орындалатын
болған жағдайда орындалатын
 - нақты санын атаймыз.
- нақты санын атаймыз.
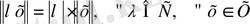 ,
,
 , егер(
, егер(
 )
)
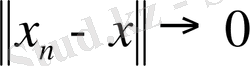 болса
болса
және
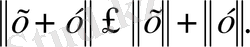 - ”үшбұрыш теңсіздігі„ орындалса
- ”үшбұрыш теңсіздігі„ орындалса
 сызықтық кеңістігіндегі екі түрлі
сызықтық кеңістігіндегі екі түрлі
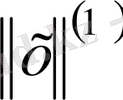 және
және
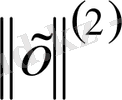 нормасын енгізейік.
нормасын енгізейік.
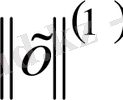 және
және
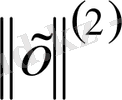 номалары эквивалентті деп аталады, егер кез келген
номалары эквивалентті деп аталады, егер кез келген
 үшін
үшін
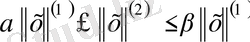 теңсіздігі орындалатындай
теңсіздігі орындалатындай
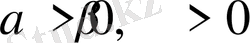 сандары табылса. Бұдан еуі норма сызықтық кеңістікте эквивалентті
сандары табылса. Бұдан еуі норма сызықтық кеңістікте эквивалентті
 әрқайсысы бір-біріне тәуелді болатыны анық. Бұл жағдайда егер
Х
сызықтық кеңістігінде екі эквивалентті норма және
Х
1
және
Х
2
- сәйкесінше нормаланған кеңістіктері берілсе, онда берілген кеңістіктердің бірінде жинақталатын қатар, екінші кеңістікте де сондай шекке жинақталады. Бұл жайт, әр кеңістікте өзімізге жұмыс істеуге ыңғайлы эквивалентті нормалардың бірін таңдауға мүмкіндік береді.
әрқайсысы бір-біріне тәуелді болатыны анық. Бұл жағдайда егер
Х
сызықтық кеңістігінде екі эквивалентті норма және
Х
1
және
Х
2
- сәйкесінше нормаланған кеңістіктері берілсе, онда берілген кеңістіктердің бірінде жинақталатын қатар, екінші кеңістікте де сондай шекке жинақталады. Бұл жайт, әр кеңістікте өзімізге жұмыс істеуге ыңғайлы эквивалентті нормалардың бірін таңдауға мүмкіндік береді.
Егер қарастырып отырған Х кеңістігіміз - ақырлы өлшемді болған жағдайда, норманы таңдау кеңістікті өзгертпейді. Анығырақ: Кез келген ақырлы өлшемді сызықтық кеңістікте барлық нормалар эквивалентті.
Мысал 3. 1.
Евклид кеңістігі
.
 -сызықты жүйесі мүмкін болатын барлық
n
- өлшемді
-сызықты жүйесі мүмкін болатын барлық
n
- өлшемді
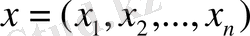 векторларынан құралсын.
векторларынан құралсын.
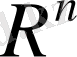 . Егер
. Егер
 - кеңістігінде келесі нормалардың бірін енгізе алсақ, яғни
- кеңістігінде келесі нормалардың бірін енгізе алсақ, яғни
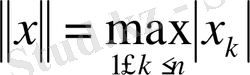 немесе
немесе
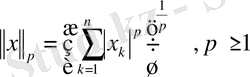 , онда
, онда
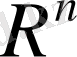 -
евклидтік кеңістігі деп аталатын нормаланған кеңістікті аламыз. Нормалардың аксиомалары сөзсіз тексеріледі. Бұл кезде, екінші норма үшін үшбұрыш теңсіздігі ақырлы қосынды үшін Минковский теңсіздігінің қолдану салдары болып табылады.
-
евклидтік кеңістігі деп аталатын нормаланған кеңістікті аламыз. Нормалардың аксиомалары сөзсіз тексеріледі. Бұл кезде, екінші норма үшін үшбұрыш теңсіздігі ақырлы қосынды үшін Минковский теңсіздігінің қолдану салдары болып табылады.
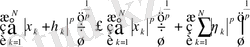 .
.
Егер векторлар «координатасы» комплекс сандар болса, онда
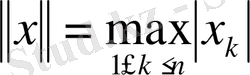 немесе
немесе
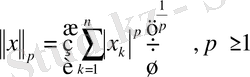 ,
,
(мүндағы
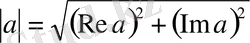 -
-
 -комплекс санның модулі) нормасымен анықталған
-комплекс санның модулі) нормасымен анықталған
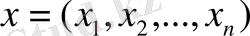 векторының комплекс бағанынан құралған сызықтық система нормаланған кеңсітік болып және евклидтік кеңістік тәріздес
векторының комплекс бағанынан құралған сызықтық система нормаланған кеңсітік болып және евклидтік кеңістік тәріздес
 деп белгіленеді.
деп белгіленеді.
 нүктесі
нүктесі
 жиынының шектік нүктесі деп аталады, егер
жиынының шектік нүктесі деп аталады, егер
 нүктесінің кез келген маңайында
нүктесінің кез келген маңайында
 нүктесінен өзге болатын М жиынының кемінде бір нүктесі жатса. Басқа сөзбен айтқанда,
нүктесінен өзге болатын М жиынының кемінде бір нүктесі жатса. Басқа сөзбен айтқанда,
 -
-
 жиынының шектік нүктесі дейміз, егер кез келген
жиынының шектік нүктесі дейміз, егер кез келген
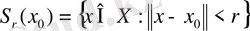 шарында
шарында
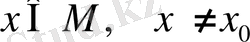 нүктесі табылса.
нүктесі табылса.
 нүктесі
нүктесі
 жиынының шектік нүктесі болуы үшін
жиынының шектік нүктесі болуы үшін
 ,
,
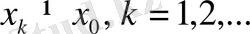 . нүктесіне жинақталатын
. нүктесіне жинақталатын
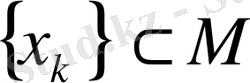 тізбегінің бар болуы қажетті және жеткілікті.
тізбегінің бар болуы қажетті және жеткілікті.
, ал
- М жиынының шектік нүктелер жиыны болсын. Онда
жиыны М жиынының тұйықталуы деп аталады. Басқа сөзбен айтқанда,
- бұл құрамында М жиыны бар өте кішкентай тұйық жиын.
болатын М жиыны тұйық деп немесе берілген жиын тұйық деп аталады, егер шектік нүктелерінің бәрі өзінде жатса.
сызықтық кеңістігіндегі
жиыны сызықты көпбейнелік деп талады, егер кез келген
және
сандары үшін
сызықтық комбинациясы
жиынында жатса.
жиыны
жиынының бір бөлігі болғандықтан, сызықты көпбейнеліктің анықтамасынан
жиыны да сызықтық кеңістік екендігі шығады. Мұндай
жиыны нормасы бойынша
жиынында тұйық болмайтынын ескерту қажет.
 (
(
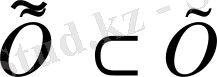 ) нормаланған кеңістігінде жататын
) нормаланған кеңістігінде жататын
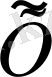 сызықты көпбейнелігін
сызықты көпбейнелігін
 жиынында тығыз дейміз, егер
жиынында тығыз дейміз, егер
 и
и
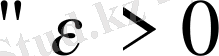 саны үшін
саны үшін
 теңсіздігі орындалатындай
теңсіздігі орындалатындай
 элементі табылса. Демек, егер
элементі табылса. Демек, егер
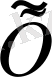
 жиынында тығыз болса, онда
жиынында тығыз болса, онда
 үшін
үшін
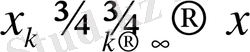 болатындай
болатындай
 тізбегі табылады.
тізбегі табылады.
Жоғарыда айтылған анықтаманы тұйықталумен салыстырсақ, «
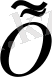 жиыны
жиыны
 жиынында тығыз»,
жиынында тығыз»,
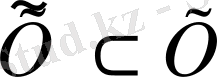 ,
,
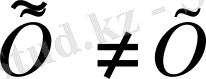 тұжырымы
тұжырымы
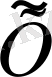 сызықты көпбейнеліктің
сызықты көпбейнеліктің
 нормасы бойынша тұйықталуы
нормасы бойынша тұйықталуы
 -пен сәйкес келетінін байқаймыз. Бұл кезде,
-пен сәйкес келетінін байқаймыз. Бұл кезде,
 кеңістігін
кеңістігін
 нормасы бойынша
нормасы бойынша
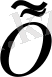 сызықты көпбейнеліктің толықтырушысы деп те атаймыз. Әрбір сызықты нормаланған
сызықты көпбейнеліктің толықтырушысы деп те атаймыз. Әрбір сызықты нормаланған
 кеңістігінің толықтырушысы бар және бұл толықтырушы
кеңістігінің толықтырушысы бар және бұл толықтырушы
 -ті өзіне көшіретін изометриялық бейнесіне дейін дәл болатын жалғыз жиын.
-ті өзіне көшіретін изометриялық бейнесіне дейін дәл болатын жалғыз жиын.
Спектральді теорияның ең басты сұрақтарының бірі- меншікті және қосалқы функциялар жүйесінің толықтығын қарастырып отырған кеңістікте зерттеу.
 кеңістігіндегі
кеңістігіндегі
 жүйесінің толықтығы көбінесе
жүйесінің толықтығы көбінесе
 векторына тартылған, яғни
векторына тартылған, яғни
 векторының барлық сызықты комбинациясынан құралған сызықты көпбейнеліктің Х жиынында барлық жерде дерлік тығыз екенін дәлелдеу нәтижесінен шығады. Берілген элементтердің қарастырып отырған кеңістікте сызықты қабықшасы тығыз болуы үщін «жиі» немесе «жақын» орналасуы қажеттігі туралы келесі теоремада айтылады.
векторының барлық сызықты комбинациясынан құралған сызықты көпбейнеліктің Х жиынында барлық жерде дерлік тығыз екенін дәлелдеу нәтижесінен шығады. Берілген элементтердің қарастырып отырған кеңістікте сызықты қабықшасы тығыз болуы үщін «жиі» немесе «жақын» орналасуы қажеттігі туралы келесі теоремада айтылады.
Теорема 3. 1.
(
Мюнц
) .
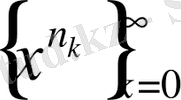 функциясының сызықты қабықшасы (мұндағы
функциясының сызықты қабықшасы (мұндағы
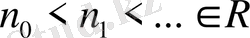 ,
,
 )
)
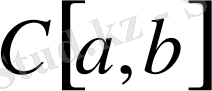 кеңістігінде тығыз болуы үшін
кеңістігінде тығыз болуы үшін
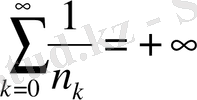 қатарының жинақталуы қажетті және жеткілікті.
қатарының жинақталуы қажетті және жеткілікті.
Нормаланған кеңістіктердің толықтығын түсіндіру үшін келесі лемманы қарастырайық.
Лемма 3. 1.
(
тізбектердің жинақталуы туралы
) . Кез келген
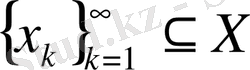 жиыны үшін нормаланған (толық емес болуы мүмкін)
жиыны үшін нормаланған (толық емес болуы мүмкін)
 кеңістігінде келесі тұжырымдар эквивалентті:
кеңістігінде келесі тұжырымдар эквивалентті:
1)
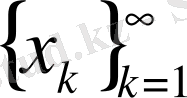 жинақталады;
жинақталады;
2)
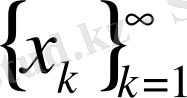 -тізбегінің кез келген
-тізбегінің кез келген
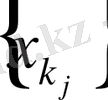 -тізбекшесі жинақталады;
-тізбекшесі жинақталады;
3)
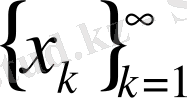 -тізбегі фундаментальді және берілген
-тізбегі фундаментальді және берілген
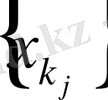 - тізбекшесі жинақталады;
- тізбекшесі жинақталады;
4)
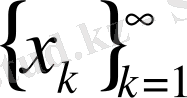 -тізбегі фундаментальді және
-тізбегі фундаментальді және
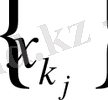 - жинақталатын тізбекшесі бар;
- жинақталатын тізбекшесі бар;
5)
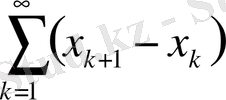 - қатары жинақталады.
- қатары жинақталады.
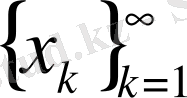 тізбегінің тізбекшесі деп,
тізбегінің тізбекшесі деп,
 , ретімен құралған
, ретімен құралған
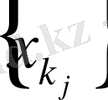 тізбекті айтамыз, яғни
тізбекті айтамыз, яғни
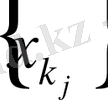 тізбекшесінің
тізбекшесінің
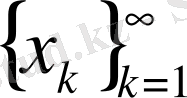 тізбегінің элементтерінің реті сақталады екен.
тізбегінің элементтерінің реті сақталады екен.
1. 3. 2. Гильберт кеңістігі.
Көптеген есептерде ерекше дербес жағдай туындайды, егер
 сызықтық кеңістігінде евклидтік кеңістігіндегі қарапайым скалярлық көбейтіндінің жалпылауы болатын скалярлық көбейтіндіні енгізсек. Яғни,
x
,
у
сызықтық кеңістігінде евклидтік кеңістігіндегі қарапайым скалярлық көбейтіндінің жалпылауы болатын скалярлық көбейтіндіні енгізсек. Яғни,
x
,
у

 элементтерінің скалярлық көбейтіндісі деп, (
x
,
у
) деп белгіленетін келесі қасиеттерді қанағаттандыратын комплекс санды айтамыз.
элементтерінің скалярлық көбейтіндісі деп, (
x
,
у
) деп белгіленетін келесі қасиеттерді қанағаттандыратын комплекс санды айтамыз.
- Барлық кезде (x, x) 0 және (x, x) = 0, тек қанаx= 0 болған жағдайында ;
- ;
- , кез келгенС.
саны норманың барлық аксиомаларын қанағаттандырады. Сондықтан, x элементінің нормасы ретінде
санын аламыз. Бұндай кеңістікті сыртқы Гильберт кеңістігі деп атаймыз. Функционалдық талдауды негіздеу үшін, қарастырып отырған кеңістіктің толық болғандығы маңызды ( кеңістіктің элементтерінің фундаментальді тізбегі осы кеңістіктің элементіне жинақталуы үшін, яғни кез келген x m , x n
Х үшін n, m →∞ , x n - x m → болса, онда Х жиынының элементі болатындай
шегі табылады) .
Толық сызықты нормаланған және толық сыртқы гильберт кеңістігі, сәйкесінше, банах және гильберт кеңістігі деп аталады. Бұл жағдайда, метрикалық кеңістіктің толықтыруы ретінде (рационал саннан нақты санға өтуі) сызықты нормаланған кеңістік банах (гильберт) кеңістігіне келтіреді.
Егер кеңістіктегі норма
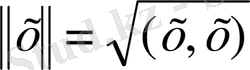 скалярлық көбейтіндіден туындаса, онда «параллелограмм тепе-теңдігі орындалады»:
скалярлық көбейтіндіден туындаса, онда «параллелограмм тепе-теңдігі орындалады»:
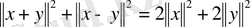 . (3. 1)
. (3. 1)
Кәдімгі евклидтік кеңістік гильберт кеңістігінің қарапайым мысалы бола алады. Гильберт кеңістігі ретінде комплексті бағандардың
 кеңістігін де алуға болады және онда скалярлық көбейтінді келесі формуламен анықталады:
кеңістігін де алуға болады және онда скалярлық көбейтінді келесі формуламен анықталады:
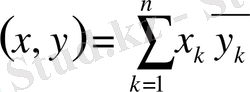 для всех
для всех
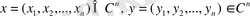 .
.
Бірақ, функционалдық талдауда басты рөлді ақырсыз өлшемді кеңістіктер, яғни сызықты тәуелсіз векторлардың ақырсыз санынан құралған кеңістіктер атқарады.
Осындай кеңістіктердің мысалын келтірейік.
1. 3. 3. Функционалдық кеңістіктердің негізгі мысалдары.
Мысал 3. 2.
Элементтері -
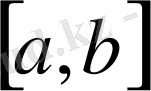 тұйық интервалында
тұйық интервалында
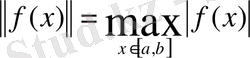 нормасымен анықталған үзіліссіз комплексмәнді функциялар болатын Банах кеңістігі. Бұл кезде
нормасымен анықталған үзіліссіз комплексмәнді функциялар болатын Банах кеңістігі. Бұл кезде
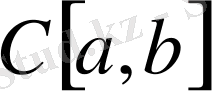 кеңістігінде норма бойынша жинақталу- математикалық анализ курсынан белгілі бірқалыпты жинақталу болып табылады.
кеңістігінде норма бойынша жинақталу- математикалық анализ курсынан белгілі бірқалыпты жинақталу болып табылады.
Мысал 3. 3.
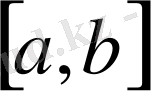 тұйық интервалында
тұйық интервалында
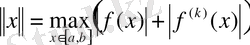 , (мұндағы
, (мұндағы
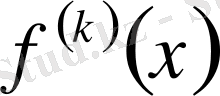 - к-ші ретті
f(x)
функциясының туындысы) нормасымен анықталған комплексмәнді үзіліссіз дифференциалданатын функцияларынан құралған
- к-ші ретті
f(x)
функциясының туындысы) нормасымен анықталған комплексмәнді үзіліссіз дифференциалданатын функцияларынан құралған
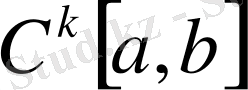 Банах кеңістігі.
Банах кеңістігі.
 - тізбегінің жинақталуы - бұл
- тізбегінің жинақталуы - бұл
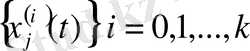 тізбектерінің
тізбектерінің
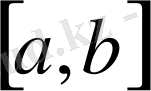 интервалындағы бірқалыпты жинақталу.
интервалындағы бірқалыпты жинақталу.
Мысал 3. 4.
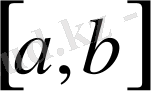 интервалында
интервалында
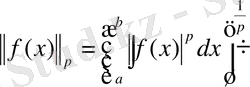 (
p
1) функция дәрежесімен анықталған барлық
р
бойынша қосындыланатын
(
p
1) функция дәрежесімен анықталған барлық
р
бойынша қосындыланатын
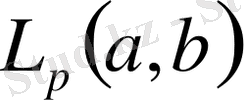 Банах кеңістігі.
Банах кеңістігі.
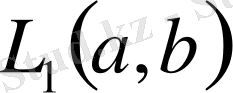 кеңістігіндегі норма бойынша жинақталу деп, ал
кеңістігіндегі норма бойынша жинақталу деп, ал
 -
кеңістігіндегі норма бойынша тізбектердің жинақталуын орташа квадраттық жинақталу деп атайды.
-
кеңістігіндегі норма бойынша тізбектердің жинақталуын орташа квадраттық жинақталу деп атайды.
Мысал 3. 5.
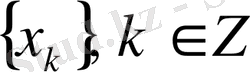 (бүтін сандар жиыны) ақырсыз тізбектерінің
(бүтін сандар жиыны) ақырсыз тізбектерінің
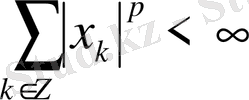 , ал нормасы
, ал нормасы
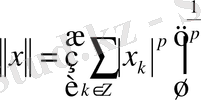 бойынша анықталатын
бойынша анықталатын
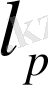 -Банах кеңістігі.
-Банах кеңістігі.
Мысал 3. 6.
p
= 2 жағдайында
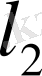 және
және
 - гильберт кеңістіктері, мысалы,
- гильберт кеңістіктері, мысалы,
 -да скалярлық көбейтінді
-да скалярлық көбейтінді
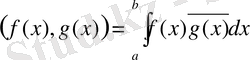 .
.
және
кеңістіктері
жағдайында Гильберт кеңістігі бола алмайтындығына оңай көз жеткізуге болады, өйткені бұл кеңістіктерге енгізілген нормалар (3. 1) параллелограмм тепе- теңдігін қанағаттандырады.
Бұл кеңістіктердің барлығы ақырсыз өлшемді, бұл
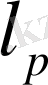 үшін оңай көрсетіледі:
үшін оңай көрсетіледі:
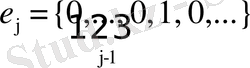 -саналатын векторлар саны сызықты тәуелсіз.
-саналатын векторлар саны сызықты тәуелсіз.
1. 3. 4. Лебег интегралы ұғымы.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz