Коши теңсіздігі: орта мектептегі теңсіздіктерді дәлелдеудегі қолданылуы


Қазақстан Республикасы Білім және Ғылым Министрлігі
Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті
Шымкент институты
Жоғары математика кафедрасы
Е. Исаев - 050109 «Математика мұғалімі»
мамандығының күндізгі оқу бөлімінің
4 курсындағы 12-26 тобының студенты
ДИПЛОМДЫҚ ЖҰМЫС
«Коши теңсіздікі және оның орта мектепте теңсіздіктерді дәлелдеуге қолданылуы»
Ғылыми жетекшісі : Жоғары математика кафердрасының
доценті Ж. Қырғызбаев
Шымкент 2010
Қазақстан Республикасы Білім және Ғылым Министрлігі
Қ. А. Ясауи атындағы Халықаралық қазақ-түрік университеті
Шымкент институты
Жоғары математика кафедрасы
«Қорғауға жіберілсін»
Жоғары математика
Кафедрасының меңгерушісі,
Доцент К. Абдурахманов
«___» 2010 ж.
ДИПЛОМДЫҚ ЖҰМЫС
«Коши теңсіздікі және оның орта мектепте теңсіздіктерді дәлелдеуге қолданылуы»
Орындаған : Физика-математика факультетінің 4 курсындағы
12-26 тобының студенті Е. Исаев
Ғылыми жетекшісі : Жоғары математика кафердрасының
доценті Ж. Қырғызбаев
Шымкент 2010
Мазмұны
Кіріспе . . . 3
1. Арифметикалық орта мен игеометриялық ортаны
салыстыру . . . 4
2. Коши теңсіздігі және оның теңсіздіктерді дәлелдеуде
қолданылуы . . . 10
3. Коши теңсіздігі және оның орта мектепте теңдеулер мен
олардың жүйелерін шешуде қолдануы . . . 46
4. Теңсіздіктерді дәлелдеуге берілген есептер . . . 55
Қорытынды . . . 59
Пайдаланылатын әдебиеттер . . . 60
Кіріспе
Өмірде абсолют бірдей өзароа тең екі нәрсені табу қиын. Сондықтан да бізге теңдеулермен емес, көбшнесе теңсіздіктермен араласуға тура келеді. Теңсіздіктермен адам баласы өте ертеде балалық шағынан бастап кездеседі. Мысалы, бастауыш сыныптарда қарапайым теңсіздіктер қарастырылады. Алайда теңсіздіктердің негізі қасиеті алғаш рет 9-сыныптарда алгебра курсында ғана қарастырылады.
Негізгі мектеп пен орта мектептегі ең күрделі және оқушыларга қиын тақырыптардың бірі - теңсіздіктерді дәлелдеу болып табылады. Орта мектептерде теңсіздіктерді кейбір қарапайым тәсілдері ғана қарастырылады. Теңсіздіктерді дәлелдеуге берілген есептерде көбінесе орташа шамалардың негізгі қасиеттері қолданылады. Сондықтан да оқушыларға орта мектептерде орташа шамалардың түрлерін және олардың арасындағыт орындалатын арақатыстарды таныстырған тиімді. Мұғалімдерге көмекші құрал ретінде ұсынылып отырған бұл дипломдық жұмыста орташа шамалардың теңсіздіктерді дәлелдеуде қолданылуы қарастырылған.
Дипломдық жұмыс кіріспеден және төрт параграфтан, қорытынды мен әдебиеттер тізімінен тұрады.
Дипломдық жұмыстың кіріспесінде жұмыстың мақсаты, ал оның алғашкы 1-ші параграфында арифметикалық орта мен геометриялық ортаның арасындағы негізгі арақатыс қарастырылған.
Жұмыстың келесі 2-ші параграфында Коши теңсіздігі және оның теңсіздіктерді дәлелдеуге қолданылуы баяндалған.
Дипломдық жұмыстың бұдан кейінгі 3-ші параграфында Коши теңсіздігін теңдеулер мен олардың жүйелерін шешу мәселері қарастырылған.
4-ші параграфта Коши теңсіздігін қолданып, дәлелденетін теңсіздіктерге жаттығулар құрастырылған.
Жұмыстың соңында қорытынды мен әдебиеттер тізімі келтірілген.
1. Арифметикалық орта мен игеометриялық ортаны салыстыру
Мына екі шаманы салыстыруды алдымызға мақсат етіп қоялық.
Қайсысы улкен:
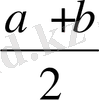 немесе
немесе
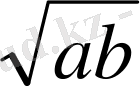 ?
?
Айталық бізге екінші мүшесінен бастап әрбір мүшесі өзінің алдында тұрған мүшесіне бірдей сен 3-ті қосқанда шығатын, яғни мүшелері арифметикалық прогрессия құратын мынадай тізбек берілсін: 2, 5, 8, 11, 14, . . .
Бұл тізбектің мынадай қасаиеті бар: қатар туұрған кез келген үш мүшесінің ортадағысы шекті мүшелерінің қосындысының жартысына тең. Мысалы: 5, 8, 11
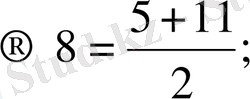 8, 11, 14
8, 11, 14
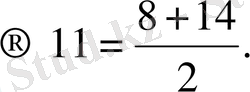
Екі санның арифметикалық ортасы
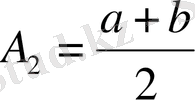 деп аталатын мұндай өрнектер математикада және өмірде жиі кездеседі.
деп аталатын мұндай өрнектер математикада және өмірде жиі кездеседі.
Мысалы: трапецияның орта сызығы оның табандарының арифметикалық ортасына тең (1-сурет) .
b
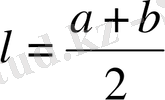
1-сурет
Кесіндінің абциссасының ортасы оның ұштарының арифметикалық ортасына тең (2-сурет) .
y
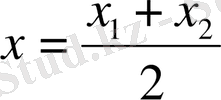
x
0 x 1 x x 2
Енді мынадай есепті қарастырайық. Трапецияның табандары a және b - ға тең. Шеңберге сырттай сызылған тең бүйірлі трапецияның биіктігін анықтаңдар.
Ш е ш у і : 3-суреттен есептің шартын пайдаланып, мынаны табамыз:
P
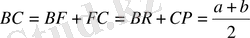 D C
D C
M F
өйткені BR=BF, CF=CP; O N
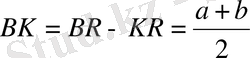 A B
A B
R K
Демек,
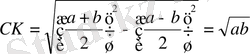
Бұл өрнекті екі санның геометриялық ортасы деп айтады. Оны Г
2
=
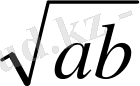 арқылы белгілейік.
арқылы белгілейік.
Екі санның геометриялық ортасы да орта мектепте жиі кездеседі. Мысалы, мүшелері оң таңбалы геометриялық прогрессияның кез келген мүшесі алдыңғы мүшесімен жалғас мүшелерінің геометриялық ортасына тең болады.
Тік бұрышты үшбұрыштың тік бұрышынан гипотенузасына түсірілген биіктік гипотенузаның табандарын бөлетін кесінділердің геометриялық ортасына тең болады (4-сурет) .
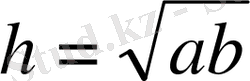
h
a b
4-сурет
Тік бұрышты үшбұрыштың катеті гипотенузасы мен өзінің оған түсірілген проекциясының геометриялық ортасына тең болады (5-сурет) .
x
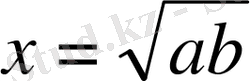
b
a
5-сурет
Трапецияны екі ұқсас трапецияға бөлетін табандарына параллель жүргізілген түзу трапецияның табандарының геометриялық ортасы болып табылады.
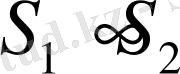 ,
,
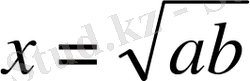
Енді осы екі оң таңбалы а және b сандарының арифметикалық ортасы мен геометриялық ортасын өзара салыстырайық. Айталық, a=1, b=4 болсын. Сонда
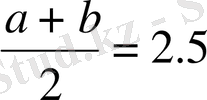 және
және
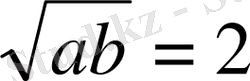 болатындықтан, мынаны байқаймыз:
болатындықтан, мынаны байқаймыз:
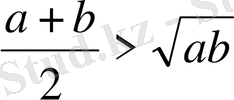 . Барлық уақытта осылай ма?
. Барлық уақытта осылай ма?
Мұні біз 3-суреттен де байқаған едік. MN-трапецияның орта сызығы боғандықтан, ол дөңгелектің диаметрінен улкен, яғни
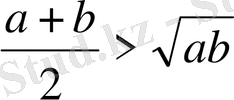 болады. Осы теңсіздіктің тағы да екі геометриялық дәлелдемесін келтірейік.
болады. Осы теңсіздіктің тағы да екі геометриялық дәлелдемесін келтірейік.
ІІ-тәсіл. Жарты шеңберге іштей сызылған тік бұрышты АВС үшбұрышын қарастырайық. С = 90 0 , CD-оның биіктігі.
Айталық, AB > BC, AD = a, DB = b болсын.
Сонда
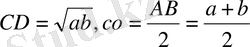 және CD<CO болатындығын ескерсек, онда
және CD<CO болатындығын ескерсек, онда
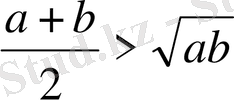 болып шығады.
болып шығады.
ІІІ-тәсіл. Айталық радиустары R мен r-ге тең екі шеңбер өзара сырттай жанассын (6-сурет) . Сонда -нан мынаны табамыз:
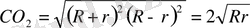 .
.
Ал бірак
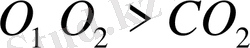 , cондықтан
, cондықтан
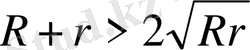 немесе
немесе
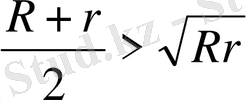 O
1 R
O
1 R
C r
O 2
A B
6-сурет
Бұл екі қарастырылған мысалда біз
 болатындығын көреміз.
болатындығын көреміз.
a>0 және b>0 болғанда, бұл теңсіздік әр уақытта тура бола ма?
Жоғарыдағы теңсіздіктің дұрыстығын былайда дәлелдеп көрсетуге болвады. Мына айырманы қарастырайық:
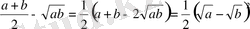
Бұдан егер
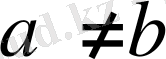 болса, онда
болса, онда
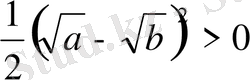 болатындығын, ал егер a=b болса, онда
болатындығын, ал егер a=b болса, онда
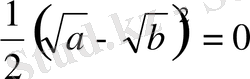 болатындығын көреміз.
болатындығын көреміз.
Сонымен, теріс емес екі оң санның арифмтикалық ортасы олардың геометриялық ортасынан кем болмайтындығын дәлелдедік:
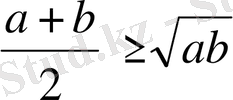 . Теңдік белгісі a=b болған жағдайда ғана орындалады.
. Теңдік белгісі a=b болған жағдайда ғана орындалады.
Толық математикалық индукция әдісін қолданып, бірнеше оң сандардың арифметикалық ортасының олардың геометриялық ортасынан, кем еместігін яғни

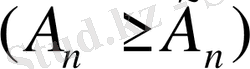 (1)
(1)
дәлелдеп көрсетуге болады. Теңдік белгісі тек
 болған жағдайдағана орындалады. (1) теңсіздікті Коши теңсіздшіш деп айтады.
болған жағдайдағана орындалады. (1) теңсіздікті Коши теңсіздшіш деп айтады.
(1) теңсіздікті дәлелдеудің бірнеше (әртүрлі) тәсілдері бар. Бірақ олардың ішіндегі жеңілі жоқ. Бұлардың әрқайсысында өзіндік тапқырлық, өзіндік ізденіс бар. Бұл мында (1) теңсіздіктің француздың көрнекті математигі Коши (1789-1857) берген дәлелдемесін келтірумен шектелеміз.
(1) теңсіздіктің n = 1 үшін дұрыстығы ақиқат, оның n = 2 үшін дұрыстығы жоғарыда дәлелденді.
Алдымен алдынала мынандай көмекші тұжырымды дәлелдейміз: егер (1) теңсіздік n = k үшән дұрыс болса, онда ол n = 2k үшін дұрыс болады. Расында да,

Сөйтіп, (1) теңсіздікті n = k үшін дұрыс деп жорығанда, оның n = 2k ушін де дұрыс болатындығын дәлелдедік. (1) теңсіздік жоғарыда n = 2 үшін дұрыстығын дәлелденген еді. Демек, ол n = 4, 8, 16, 32, . . . , яғни n = 2 l , мұндағы l-кез келген натурал сан ушін дұрыс болады.
Енді (1) теңсіздікетің кез келген натурал n саны үшін дұрыстығын дәлелдейік. Айталық n кез келген натурал сан болсын. Егер n саны 2 санының бүтін дәрежесі болып келсе, онда жоғарыдағы дәлелдегеніміз бойынша (1) теңсіздік ондай n-дер үшін дұрыс болады. Егер n саны 2 санының бүтін дәрежесі болмаса, онда n-ге сондай q санын қосып, n+q саны 2санының бүтін дәрежесі болатындай етіп шығарып алуға болады. Айталық n+q = 2 l болсын. Сонда жоғарыдағы дәлелденілген көмекші тұжырымдама бойынша мына теңсіздік орындалады:
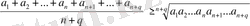 (2)
(2)
мұндағы
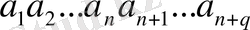 -кез келген оң сандар.
-кез келген оң сандар.
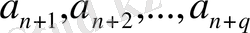 сандарын таңдап алу өз еркімізге байланысты болғандыктан,
сандарын таңдап алу өз еркімізге байланысты болғандыктан,
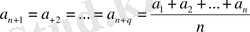 деп алайық.
деп алайық.
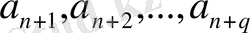 cандарын мұндай етіп таңдап алғаннан кейін (2) теңсіздік мынадай түрге келеді:
cандарын мұндай етіп таңдап алғаннан кейін (2) теңсіздік мынадай түрге келеді:

Бұдан
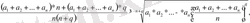
немесе

Соңгы теңсіздіктің екі жағында бірдей (n+q) дәрежеге шығарып табатынымыз:

Бұдан
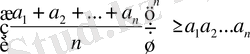
немесе:
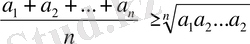
Сөйтіп, (1) теңсіздіктің кез келген натурал сан n үшін дұрыстығы дәлелденді.
Енді (1) теңсіздіктегі теңдік белгісінің барлық шамаларының тек өзара тең болған жағдайда ғана орындалатындағын корсетелік.
Ол үшін шамаларының кез келген екеуін, мысалы мен ні өзара тең емес деп алайық. Бұл жағдайда (1) формулада > таңбасының орындалатындығын, яғни
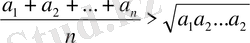 көрсетелік.
көрсетелік.
Дәлелдеуі:
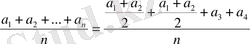 екені айқын.
екені айқын.
(1) формуланы бұл өрнектердің әрбір екеуне қолданып, мынаны табамыз:
 (3)
(3)
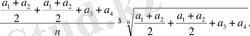 (4)
(4)
Егер
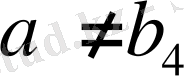 болса, онда
болса, онда
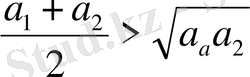 және
және
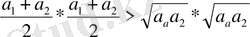 Демек, болғанда (4) теңсіздіктің оң жағы (3) теңсіздіктің оң жағынан артық, ал олардың сол жақтары өзара тең. Сондықтан (3) теңсіздікте теңдік белгісінің орындалуы мүмкін емс, яғни шамаларының кем дегенде екеуі өзара тең болмаған жағдайда
Демек, болғанда (4) теңсіздіктің оң жағы (3) теңсіздіктің оң жағынан артық, ал олардың сол жақтары өзара тең. Сондықтан (3) теңсіздікте теңдік белгісінің орындалуы мүмкін емс, яғни шамаларының кем дегенде екеуі өзара тең болмаған жағдайда
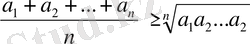 теңсіздігі орындалады.
теңсіздігі орындалады.
Сонымен, Коши теңсіздігінің дұрыстығы толығымен дәлелденді.
2. Коши теңсіздігі және оның теңсіздіктерді дәлелдеуде қолданылуы
Бірнеше оң сандардың арифметикалық ортасы мен геометриялық ортасы байланыстарын Коши теңсіздігі орта мектепте теңсіздіктердің дұрыстығын дәлелдеуге өте жиі қолданылады.
Енді соған мысалдар қарастырайық.
1-мысал.
Теңсіздікті дәлелдеңдер:
 (мұндағы a>0, b>0, c>0)
(мұндағы a>0, b>0, c>0)
Дәлелдеуі: Берілген теңсіздіктің сол жағына (1) теңсіздікті қолданып, мынаны табамыз:
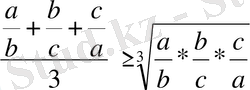 немесе
немесе
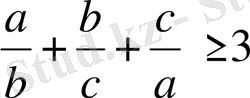
Сонымен, теңсіздіктің дұрыстығы дәлелденді.
2-мысал. Теңсіздікті дәлелдеңдер:
 (a>0, b>0, c>0, d>0)
(a>0, b>0, c>0, d>0)
Дәлелдеуі: (1) теңсіздікті қолданып, мыналарды табамыз:
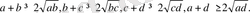
Осы теңсіздіктерді мушелеп көбейтіп, аныктайтынымыз:
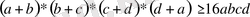
Сонымен, теңсіздіктің дұрыстығы дәлелденді.
3-мысал. Теңсіздікті дәлелдеңдер:
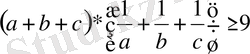 (a>0, b>0, c>0)
(a>0, b>0, c>0)
Дәлелдеуі: (1) теңсіздікті қолданып, табамыз:
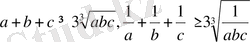
Соңғы екі теңсіздікті мүшелеп, көбейтсек
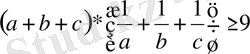 теңсіздігі келіп шығады.
теңсіздігі келіп шығады.
Сонымен, теңсіздіктің дұрыстығы дәлелденді.
4-мысал.
Оң таңбалы а, b және с сандары үшін мына теңсіздіктің орындалатындығын дәлелдеңдер:
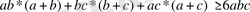
Дәлелдеуі: Теңсіздіктің екі жағында, бірдей -ға мүшелеп бөлсек, ол мынадай турге келеді:
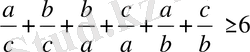 немесе
немесе
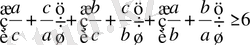 .
.
Осы теңсіздіктің сол жағында тұрған әрбір қосылғышқа (1) теңсіздікті қолдансақ:
 Осыдан
Осыдан
 немесе
немесе
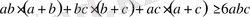
Сонымен, теңсіздіктің дұрыстыгы дәлелденді.
5-мысал: Оң таңбалы а, в және с сандары үшін мына теңсіздіктің орындалатындығын дәлелдеңдер:
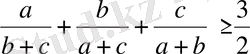 (2)
(2)
Дәлелдеуі: Теңсіздікті дәлелдеу үшін мынадай шартты белгілер енгізейік:
 , (3)
, (3)
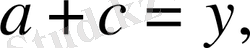 (4)
(4)
 (5)
(5)
Сонда
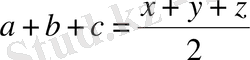 (6)
(6)
Енді (6) теңдіктен біртіндеп, (3), (4), (5) теңдіктерді мүшелеп шегерсек, онда

Бұл мәндерді (2) теңсіздікке апарып қойсақ, онда ол мынадай түрге келеді:
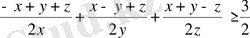 немесе
немесе
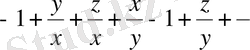
яғни

Соңғы теңсіздіктің сол жағындағы әрбір жақшаның ішінде тұрған қосылғыштар 2 - ден кем емес, сондықтан бұл теңсіздік дұрыс, олай болса, (2) теңсіздік те дұрыс болады.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
6-мысал.
Егер үшбұрыштың қабырғаларының ұзындықтары а, в, с болса, онда
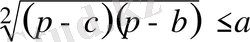 теңсіздігінің орындалатынын дәлелдеңдер, мүндағы р - жарты периметр.
теңсіздігінің орындалатынын дәлелдеңдер, мүндағы р - жарты периметр.
Шешуі:
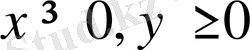 нақты сандары үшін
нақты сандары үшін
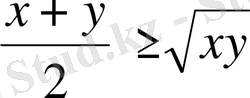 теңсіздігінің
теңсіздігінің
орындалатындығы айқын. Сонда
2р = а + в + с
болатындықтан, бүл теңсіздікке сәйкес
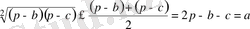 -ға ие боламыз.
-ға ие боламыз.
Осыны дәлелдеу талап етілген еді.
7-мысал. Жарты периметрі р-ға тең болатын кез келген үшбұрыштың
ауданы
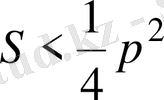 теңсіздігін дәлелдеңдер.
теңсіздігін дәлелдеңдер.
Дәлелдеуі:
 теңсіздігінің орындалатындығын көрсету жеткілікті. Герон формуласын пайдаланамыз:
теңсіздігінің орындалатындығын көрсету жеткілікті. Герон формуласын пайдаланамыз:
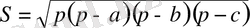
мұнда а, в, с - үшбұрыштың қабырғаларының ұзындықтары,
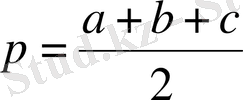
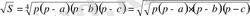
Енді Коши теңсіздігін
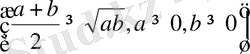 екі рет қолданамыз:
екі рет қолданамыз:
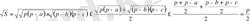
Бұл жерде теңдік белгісі тек
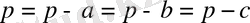 болғанда ғана орындалады. Ал бірақта, үшбұрышта
болғанда ғана орындалады. Ал бірақта, үшбұрышта
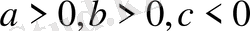 болатындықтан,
болатындықтан,
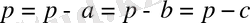 теңдігі ешқашанда орындалмайды. Демек,
теңдігі ешқашанда орындалмайды. Демек,
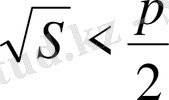 .
.
Бізден осыны дәлелдеу талап етілген еді.
8-мысал.
Егер
 болса, онда
болса, онда
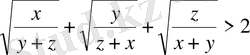 теңсіздігінің орындалатындығын дәлелдеңдер.
теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі
: Коши теңсіздігіне
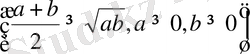 сәйкес анықтайтынымыз:
сәйкес анықтайтынымыз:
 . Теңдік белгісі
. Теңдік белгісі
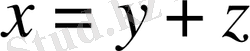 болғанда ғана орындалады.
болғанда ғана орындалады.
Дәл осылайша,
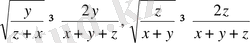 теңсіздіктерін
теңсіздіктерін
шығарып аламыз. Бұлардан
 екені келіп шығады. Теңдік белгісі
x = y + z, y = z + x, z = x + y
болғанда ғана орындалады. Оларды қоссақ,
x + y + z = 2(x + y + z),
яғни
x + y + z = 0.
екені келіп шығады. Теңдік белгісі
x = y + z, y = z + x, z = x + y
болғанда ғана орындалады. Оларды қоссақ,
x + y + z = 2(x + y + z),
яғни
x + y + z = 0.
Бұлай болуы мүмкін емес, өйткені оң сандардың қосындысы оң сан болады. Демек,
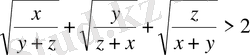
Дәлелдеу керегі де осы еді.
9-мысал. Теңсіздікті дәлелдеңдер:
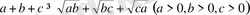
Дәлелдеуі: Коши теңсіздігіне сәйкес, мынаны табамыз:
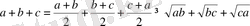
Сонымен, теңсіздіктің дұрыстыгы дәлелденді.
10-мысал. Теңсіздікті дәлелдеңдер:
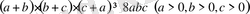
Дәлелдеуі: Коши теңсіздігін қолданып, мынаны табамыз:

Осы теңсіздіктерді мүшелеп көбейтіп, анықтайтынымыз:

Сонымен, теңсіздіктің дұрыстыгы дәлелденді.
11-мысал. Егер S = а 1 +а 2 + . . . + а п , мұндағы а х , а 2 , . . . , а п - барлығы бірдей
өзара тең емес оң таңбалы сандар болса, онда мына теңсіздіктің орындалатындығын дәлелдеңдер:
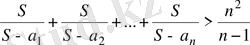
Дәлелдеуі: Арифметикалық орта мен геометриялық ортаның арасындағы арақатыс бойынша табатынымыз:
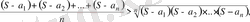
немесе
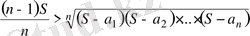 (1)
(1)
Дәл осылайша анықтайтынымыз:
 . (2)
. (2)
(1) мен (2) теңсіздікті өзара мүшелеп, көбейтіп табатынымыз:
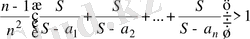 ,
,
бұдан
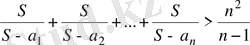
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
12-мысал. Егер үшбұрыштың қабырғаларының ұзындықтары а, в, с-ға, ал жарты периметрі р-ға тең болса, онда мына теңсіздіктің
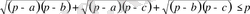
орындалатынын дәлелдеңдер.
Дәлелдеуі:
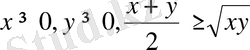 болғандықтан, мынаны табамыз:
болғандықтан, мынаны табамыз:
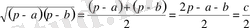 ,
,
мұндағы
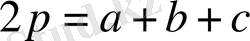 . Демек,
. Демек,
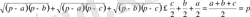
Осыны дәлелдеу талап етілген еді.
13-мысал.
Барлық натурал сан n үшін

теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі
:
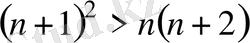 теңсіздігінің екі жағында бірдей ондық негіз бойынша логарифм десек:
теңсіздігінің екі жағында бірдей ондық негіз бойынша логарифм десек:
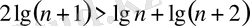
болады.
Бұдан Коши теңсіздігіне сәйкес мынау шығады:
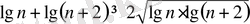
Демек,
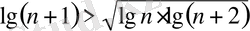
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
14-мысал.
х-тің барлық оң мәндері үшін
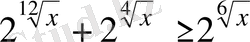 теңсіздігінің орындалатындығын дәлелдеңдер.
теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі:
Дәлелденілуге тиісті теңсіздіктің сол жағына
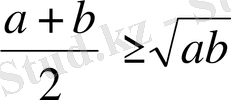
теңсіздігін қолданып, табатынымыз:
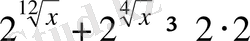
Жоғарыдағы теңсіздікті дәрежеге шығарып, анықтайтынымыз:

Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
15-мысал. Кубтың төбелеріне кез келген тәсілмен 1 ден 8-ге дейінгі
натурал сандар жазылған, оның әрбір жағына осы жағының
төбелеріндегі сандардың көбейтіндісі жазылған. Сондағы шыққан 6
санның көбейтінділерінің қосындысы N-нің 1152 ден артық
болатындығын дәлелдеңдер.
Дәлелдеуі:
Кубтың
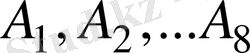 төбелерінде тұрған сандарды
төбелерінде тұрған сандарды
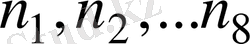 деп белгілесек, оның жағындағы сандар
деп белгілесек, оның жағындағы сандар
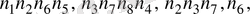
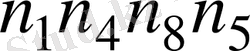 ,
,
 болады. Бұл сандардың 1 және 2, 3 және 4, 5 және 6 -лары кубтың параллель жақтарында орналасқан сандар болады. (9-сурет) . Сонда Коши теңсіздігіне сәйкес мынадай теңсіздіктер орындалады:
болады. Бұл сандардың 1 және 2, 3 және 4, 5 және 6 -лары кубтың параллель жақтарында орналасқан сандар болады. (9-сурет) . Сонда Коши теңсіздігіне сәйкес мынадай теңсіздіктер орындалады:
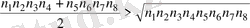 ,
,
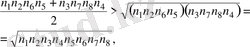 9- сурет
9- сурет
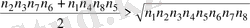
Түбір астындағы өрнек:
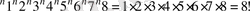 болғандықтан, бұл теңсіздіктерді мүшелеп қоссақ,
болғандықтан, бұл теңсіздіктерді мүшелеп қоссақ,
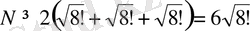 болады да, оның оң жағында тұрған саны 1152- ден артық екендігін байқау қиын емес.
болады да, оның оң жағында тұрған саны 1152- ден артық екендігін байқау қиын емес.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
16-мысал.
х>0 болғанда, натурал сан n үшін
 теңсіздігінің орындалатындығын дәлелдеңдер.
теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі. Коши теңсіздігіне сәйкес оң х 1 х 2 , . . . , х п сандары үшін
мына теңсіздіктің орындалатындығы айқын.
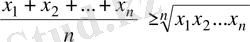
Егер
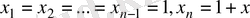 деп алсақ, онда
деп алсақ, онда
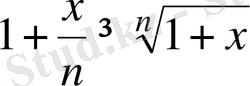 болады.
болады.
Сонымен берілген теңсіздіктің дұрыстыгы дәлелденді.
17-мысал. а-сүйір бүрышы үшін мына теңсіздіктің орындалатындығын дәлелдеңдер:
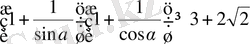
Дәлелдеуі: а>0, в>0 болғанда,
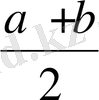 орындалатындығы айқын.
орындалатындығы айқын.
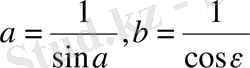 деп алсақ, онда
деп алсақ, онда
 болғандықтан, Коши
болғандықтан, Коши
теңсіздігіне сәйкес мынаны табамыз:
 Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
18-мысал.
Теңсіздікті дәлелдеңдер:
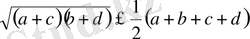
мұндағы a, b, с, -теріс емес оң сандар.
Дәлелдеуі: Теңсіздіктің дұрыстығы Коши теңсіздігінен тікелей келіп
шығады, өиткені
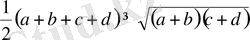
Сонымен, теңсіздіктің дұрыстыгы дәлелденді.
19-мысал.
Теңсіздікті дәлелдеңдер:
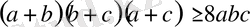 ,
,
мұндағы а, b, с-теріс емес оң сандар.
Дәлелдеуі: Коши теңсіздігін қолданып, мыналарды табамыз:

Осы теңсіздіктерді мүшелеп көбейтіп, анықтайтынымыз:
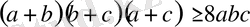
Сонымен, теңсіздіктің дұрыстығы дәлелденді.
20-мысал.
Айталық барлығы оң таңбалы
а
1
, а
2
, . . . , а
п
сандарының орын ауыстыруынан шыққан сандар болсын. Сонда
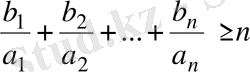 теңсіздігінің орындалатындығын дәлелдеңдер.
теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі: Коши теңсіздігіне сәйкес анықтайтынымыз:
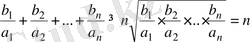
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
21-мысал.
Теңсіздікті дәлелдеңдер:
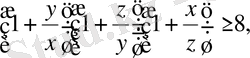

Дәлелдеуі:
Кез келген оң а саны үшін Коши теңсіздігіне сәйкес
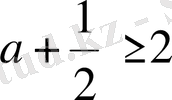 теңсіздігінің орындалатындығы белгілі. Сондықтан
теңсіздігінің орындалатындығы белгілі. Сондықтан
 теңсіздігі орындалатындығы айқын.
теңсіздігі орындалатындығы айқын.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
22-мысал. а>0 болғанда, 2а 3 +11>9а теңсіздігінің орындалатындығын
дәлелдеңдер.
Дәлелдеуі:
Оң сандардың арифметикалық ортасы олардың геометриялық ортасынан кем болмайтындықтан, Коши теңсіздігіне сәйкес мынаны табамыз:
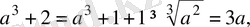
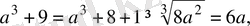
Осы екі теңсіздікті мүшелеп қосып анықтайтынымыз: 2а 3 +11>9а.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
23-мысал.
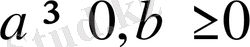 болғанда, мына теңсіздіктің
болғанда, мына теңсіздіктің
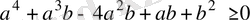 орындалатындығын дәлелдеңдер.
орындалатындығын дәлелдеңдер.
Дәлелдеуі: Теріс таңбалы емес сандардың арифметикалық ортасы
олардың геометриялық ортасынан кем болмайтындықтан,
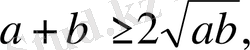
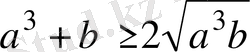 теңсіздіктері орындалады.
теңсіздіктері орындалады.
Осы теңсіздіктерді мүшелеп көбейтіп, табатынымыз:
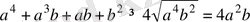 немесе
немесе
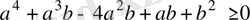
Теңдік белгісі
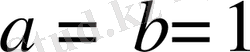 болғанда немесе
болғанда немесе
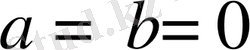 болғанда ғана орындалады.
болғанда ғана орындалады.
Сонымен, теңсіздіктің дұрыстыгы дәлелденді.
24-мысал.
а
 0
болғанда, мына теңсіздіктің орындалатындығын
0
болғанда, мына теңсіздіктің орындалатындығын
дәлелдеңдер: а 3 +3а 2 +15>13а.
Дәлелдеуі:
Коши теңсіздігіне сәйкес табатынымыз:

Осы теңсіздіктерді мүшелеп көбейтіп, анықтайтынымыз:
 немесе
немесе
 немесе
немесе
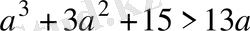
Дәлелдеу керегі де осы еді.
25-мысал.
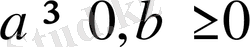 болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
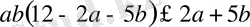
Дәлелдеуі: Коши теңсіздігіне сәйкес мына теңсіздіктердің орындалытындығы айқын:
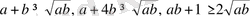
Осы теңсіздіктің алғашқы екеуін мүшелеп қосып табатынымыз:
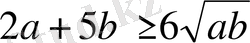
Енді осы теңсіздікті жоғарыдағы
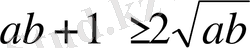 теңсіздігіне мүшелеп көбейтіп, анықтайтынымыз:
теңсіздігіне мүшелеп көбейтіп, анықтайтынымыз:
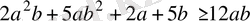 немесе
немесе
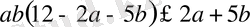
Теңдік белгісі
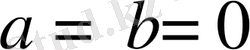 болғанда ғана орындалады.
болғанда ғана орындалады.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
26-мысал.
а
 0
болғанда мына теңсіздіктің орындалатындығын дәлеледеңдер:
а
4
+ а
3
-
8а
2
+ 4а +
4 > 0.
0
болғанда мына теңсіздіктің орындалатындығын дәлеледеңдер:
а
4
+ а
3
-
8а
2
+ 4а +
4 > 0.
Дәлелдеуі: Теріс емес сандардың арифметикалық ортасы мен геометриялық ортасының арасындағы қатыс бойынша табатынымыз:
 (1)
(1)
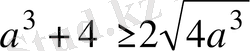 (2)
(2)
Осы теңсіздіктерді мүшелеп көбейтіп, анықтайтынмыз:
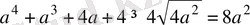 немесе
немесе

(1) теңсіздік тек болғанда ғана, ал (2) теңсіздік тек
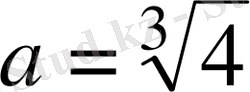 болғанда ғана тең бола алады. Демек, жоғарыдағы (1) және (2) арақатыстардың екеуі де бірдей теңдікке айналатын параметр о-ның ешқандай мәндері жоқ. Сондықтан, қатаң теңсіздік орындалады.
болғанда ғана тең бола алады. Демек, жоғарыдағы (1) және (2) арақатыстардың екеуі де бірдей теңдікке айналатын параметр о-ның ешқандай мәндері жоқ. Сондықтан, қатаң теңсіздік орындалады.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
27-мысал.
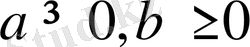 болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
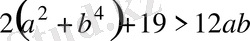
Дәлелдеуі: Коши теңсіздігіне сәйкес мынаны табамыз:
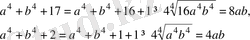
Осы екі теңсіздікті мүшелеп қосып, анықтайтынымыз:

Дәлелдеу керегі де осы еді.
28-мысал:
 болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:

Дәлелдеуі: Коши теңсіздігіне сәйкес мынаны табамыз:

Осы екі теңсіздікті мүшелеп қосып, анықтайтынымыз
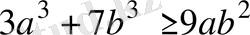
Теңдік белгісі тек
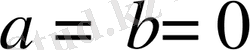 болғанда ғана орындалады.
болғанда ғана орындалады.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
29-мысал.
а-ның теріс таңбалы емес кез келген мәндерінде
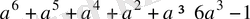 теңсіздігінің орындалатындығын дәлелдеңдер.
теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі:
І-тәсіл.
Егер
а = 0
болса, онда қатаң теңсіздік
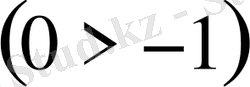 орындалады.
орындалады.
Айталық, енді
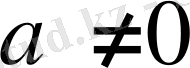 болсын. Дәлелденуге тиісті теңсіздіктің екі
болсын. Дәлелденуге тиісті теңсіздіктің екі
жағында бірдей
a
3
>0 боліп, мынаны табамыз:
 немесе
немесе
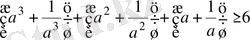
Сонда
а>0
болғанда, Коши теңсіздігіне сәйкес
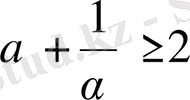
болатын-дықтан, соңғы теңсіздіктің орындалатындығы айқын.
ІІ-тәсіл.
Коши теңсіздігіне сәйкес
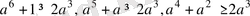
теңсіздіктерінің орындалатындығы айқын. Осы теңсіздіктерді өзара
мүшелеп қосып, анықтайтынымыз:
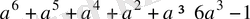
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
30-мысал.
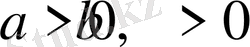 болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:

Дәлелдеуі: Дәлелденуге тиісті теңсіздікті мына түрде жазуға
болатындығы айқын:
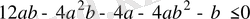
Сонда
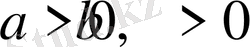 болатындықтан, бұл теңсіздіктің екі жағында
болатындықтан, бұл теңсіздіктің екі жағында
2ab
-ға бөлуге болады:
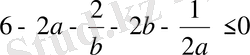 немесе
немесе

Бұдан Коши теңсіздігіне сәйкес:

болғандықтан, соңғы теңсіздіктің, одан берілген теңсіздіктің дұрыстығы келіп шығады.
Теңдік белгісі тек
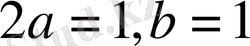 яғни
яғни
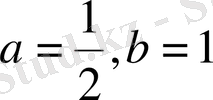 болған жағдайда ғана орындалады.
болған жағдайда ғана орындалады.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
31-мысал.
а-
ның кез келген теріс емес мәндерінде
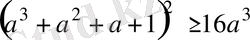 теңсіздігінің орындалатындығын дәлелдеңдер.
теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі : Дәлелденілуге тиісті теңсіздіктің екі жағыда теріс таңбалы емес, сондықтан оны мына түрде жазуға болады:
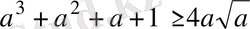 немесе
немесе
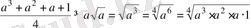
Бұл теңсіздіктің дұрыстығы ақиқат, өйткені теріс таңбалы емес сандардың арифметикалық ортасы олардың геометриялық ортасынан кем емес. Теңдік белгісі тек а 3 =а 2 =а =1, яғни а = 1 болған жағдайда ғана орындалады.
Сонымен, берілген теңсіздіктіц дұрыстыгы дәлелденді.
32-мысал.
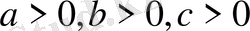 болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
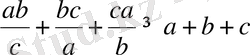
Дәлелдеуі: Коши теңсіздігіне сәйкес табатынымыз:
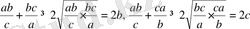
Осы үш теңсіздікті өзара мүшелеп қосып, анықтайтынымыз:
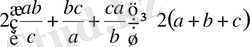 немесе
немесе
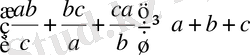
Теңдік белгісі тек а = b = с болғанда ғана орындалады.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
33-мысал.

 -
натурал сан болғанда, мына теңсіздіктің орындалатынын дәлелдеңдер:
-
натурал сан болғанда, мына теңсіздіктің орындалатынын дәлелдеңдер:
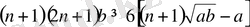
Дәлелдеуі:
Коши теңсіздігіне сәйкес
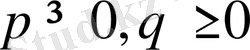 болғанда
болғанда
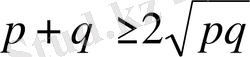
болатындықтан, төмендегі теңсіздіктер орындалады:
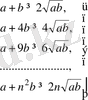 (1)
(1)
Осы (1) теңсіздіктердің барлығын өзара мүшелеп қосып, табанынымыз:
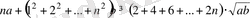 (2)
(2)
Сонда
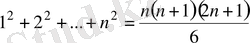 және
және
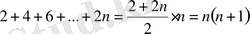
болатындықтан, (2) теңсіздікті мына түрде жазуға болады:
 немесе теңсіздікті n-ге бөлсек:
немесе теңсіздікті n-ге бөлсек:
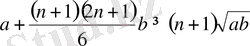 немесе
немесе
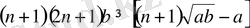
Дәлелдеу керегі де осы еді.
34-мысал.
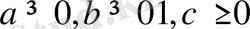 болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
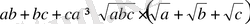 .
.
Дәлелдеуі: Коши теңсіздігіне сәйкес мына теңсіздіктің орындалатындығы айқын:
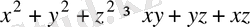 ,
,
Өйткені

Сондықтан осы теңсіздікке сәйкес анықтайтынымыз:
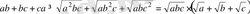
Теңдік белгісі тек a=b=c болған жағдайда ғана орындалады.
Сонымен, берілген теңсіздіктің дурыстыгы дәлелденді.
35-мысал.
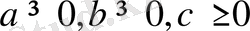 болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
болғанда, мына теңсіздіктің орындалатындығын дәлелдеңдер:
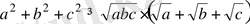
Дәлелдеуі : Коши теңсіздігіне сәйкес төмендегі теңсіздіктердің орындалатындығы айқын:
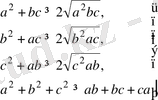 (1)
(1)
(1) теңсіздіктерді мүшелеп қосып, табатынымыз:
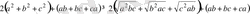
Немесе

Теңдік белгісі тек a=b=c болғанда ғана орындалады.
Сонымен, берілген теңсіздіктің дұрыстыгы дәлелденді.
36-мысал.
Егер
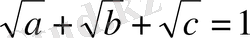 болса, онда
болса, онда

теңсіздігінің орындалатындығын дәлелдеңдер.
Дәлелдеуі : Есептің шартын мына түрде жазуға болады.
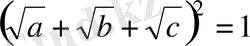
Немесе
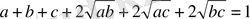 (1)
(1)
Коши теңсіздігіне сәйкес мына теңсіздіктердің орындалатындығы айқын:
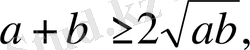 (1)
(1)
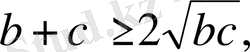 (2)
(2)
 (3)
(3)
(1), (2), (3) және (4) арақатыстарды косып, табатынымыз:

Немесе
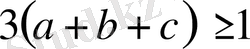
Бұдан
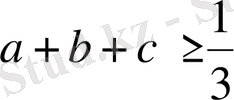
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz