Жарық интерференциясын бақылау әдістері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 45 бет
Таңдаулыға:

МАЗМҰНЫ

КІРІСПЕ

І ЖАРЫҚТЫҢ ИНТЕРФЕРЕНЦИЯСЫ

Тербелістер мен толқындардың когеренттігі және интерференция

1. 2. Жарық интерференциясын бақылау әдістері

1. 3. Толқындық шепті бөлу арқылы когерентті шоқтарды алу әдістері

1. 4 Интерференциялық жолақтардың ені

1. 5 Жарық көзі мөлшерінің интерференциялық көрініс сапасына әсері

1. 6 Жарықтың монохроматты болмауының интерференцияға әсері

1. 7 Оптикалық жол ұзындығы

1. 8 Амплитуданы бөлу арқылы оптикада когерентті шоқтарды алу амалдары

1. 9 Жұқа пленкалардың түстері

1. 10 Бірдей қалыңдық жолақтары

1. 11 Бірдей көлбеулік жолақтары

ІІ ИНТЕРФЕРЕНЦИЯ ҚҰБЫЛЫСЫНЫҢ ЗЕРТТЕУЛЕРДЕ ҚОЛДАНЫЛУЫ

2. 1 Интерференциялық аспаптар

2. 2 Екі сәулелік интерферометрлер

ІІІ ЖАРЫҚ ТАБИҒАТЫ ЖӨНІНДЕГІ КӨЗҚАРАСТЫҢ ДАМУ ТАРИХЫ

3. 1 Даму тарихы туралы қысқаша шолу

3. 2 Жарықтың толқындық теориясының шығуы

3. 3 Жарықтың корпускулалық теориясының шығуы

3. 4 Жарықтың толқындық теориясының қайта дамуы, оның электромагниттік табиғатының бекуі

3. 5 Жарықтың кванттық теориясының шығуы

ҚОРЫТЫНДЫ

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

КІРІСПЕ

Қазіргі заманғы ғылыми-техникалық прогресті үздіксіз дамытып отыруда, оптика-механикалық прибор құрылысының маңызы өте зор. Өйткені, металлургияның, машина жасау саласының, химияның, геологияның, геодезияның, медицинаның, космонавтиканың оптика-механикалық аспаптарды қолданбайынша қарқынды өркендеуі мүмкін емес.

Жұмыстың өзектілігі: Оптиканы оқыту - физика ғылымының негіздері - эксперименттік фактлерді, заңдарды, теорияларды және олардың практикалық қолданылуын, аспаптар мен құрал жабдықтарды пайдалана білу, өлшеу нәтижелерін дұрыс ала білуге үйрету. Оптикада жарық пен рентген сәулелерінің табиғаты мен қасиеттері және олардың затқа ететін әсерлері қарастырылады.

Жарық - табиғаттың, өмірдің, өндірістің, техниканың ең басты факторы. Олай болса, материяның айрықша формасы - жарық туралы оқушылардың бойында диалектикалық материалистік көзқарасты қалыптастыру - оптиканы оқытудың басты қажеттілігі болып табылады.

Жұмыстың мақсаты: Жарықтың толқындық қасиетін оқыту барысында табиғаты әр түрлі тербелістер мен толқындар туралы оқушылардың түсініктері жалпыланып қорытындыланады және олар жарықтың табиғаты жөніндегі көзқарастың дамуымен танысады. Жарықтың кванттық қасиетін оқыту барысында оқушыларда оның фотондар ағыны екендігі көзқарас қалыптасып, оны растайтын фотоэффект, Комптон-эффект, жарықтың қысымы, фотохимиялық реакция сияқты құбылыстармен танысады.

Жарық жөніндегі ілімнің даму тарихы оқушыларға таным процесінің шексіз екендігін және оның диалектикалық сипатын толық ашып көрсетуге көмегін тигізеді.

Бұл жұмыста жарықтың қасиеттерін жеткілікті жоғары дәрежеде оқыту барысында оқушылар толқындық-корпускулалық дуализмдік қасиет тек фотондарға ғана емес, барлық бөлшектерге тән қасиет екендігін дұрыс ұғына білетіндігі қарастырылады.

І ЖАРЫҚТЫҢ ИНТЕРФЕРЕНЦИЯСЫ

1. 1. Тербелістер мен толқындардың когеренттігі және интерференция

Күнделікті тәжірибеден жақсы белгілі нәрсе, екі жарық көзінің бақылау жүргізілетін қалқаның (экранның) кез-келген нүктесін жарықтандыруы әрбір жарық көзінің жеке жарықтандыруларының қосындысына тең болатындығы. Осы эмпирикалық заң (фотометриялық қосылу заңы) аумақты жарық көзінің әртүрлі бөліктері шығаратын жарығына да қолданылады.

Суперпозиция принципіне сәйкес бір толқынның жарық векторы басқа толқынның жарық векторымен ешқандай өзгеріске ұшырамай-ақ қосылады. Осының нәтижесінде амплитудасы қосылатын толқындардың амплитудалары қосындысына тең толқын алынуы мүмкін. Ал толқын энергиясы амплитуданың квадратына пропорционал болатындықтан, қорытқы толқын энергиясы, жалпы алғанда, қосылатын толқындардың энергиялары қосындысына тең болмайды; өйткені бірнеше шамалардың қосындысының квадраты бұлардың квадраттарының қосындысына тең болмайды. Сонымен тәжірибе деректері бір қарағанда жарық жайындағы толқындық түсініктермен қайшы келетін сияқты. Бұдан басқа, бірқатар бұрыннан белгілі оптикалық құбылыстарда жарықталудың кезектесіп келетін максимум мен минимумдар, максимум және минимум жарықталулардың кезектесуі, яғни кеңістікте жарық энергиясы ағынының қайта үлестірілуі байқалады. Екі жарық шоғы қосылып қараңғылық туғыза алады. 1801 ж. ашылған (Юнг) осы ғажайып құбылыс жарықтың интерференциясы деп аталады. Осындай құбылыстар геометриялық оптика шеңберінде түсіндірілмейді. Жарықты толқын деп қарастырғанда ғана интерференцияны сәтті түсіндіруге болады. Осылай, жарықтың электромагниттік табиғаты ашылудан көп бұрын жарықтың толқын екендігі тағайындалды.

Әрине, осы аталған деректердің бәрі қандай да бір жалпы теориялық түсініктер тұрғысынан түсіндірілуі тиіс, яғни теория интерференциялық жолақтардың алынуы үшін қандай шарттардың орындалуы қажет екендігін көрсетуі, неліктен әдеттегі жарықтандыру жағдайында интерференциялық жолақтардың байқалмайтындығын түсіндіруі тиіс.

Периодтары бірдей бір бағытта тербелетін екі гармоникалық тербеліс

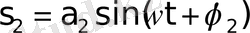; (1)

қосылған кезде қайтадан гармоникалық тербеліс

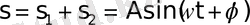(2)

алынады; мұндағы 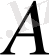-оның амплитудасы:

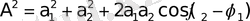(3)

(3) өрнегінен қорытқы тербеліс амплитудасының квадраты қосылатын тербелістердің амплитудалары квадраттарының қосындысына тең емес, яғни қосынды тербеліс энергиясы жеке тербеліс энергияларының қосындысына тең болмайтындығы келіп шығады. Қосылу нәтижесі бастапқы тербелістердің фазалары ( ) айырымына тәуелді болады.

Ескеретін нәрсе, таза гармоникалық тербелістер, яғни амплитудасы өзгермейтін шексіз ұзақ созылатын тербелістер болмайтындығы белгілі. Кез-келген нақты тербеліс белгілі уақытқа созылады, бұдан кейін оның үзілуі мүмкін, содан қайтадан, бірақ басқа фазада пайда болуы, тағы да үзілуі мүмкін т. т. Осы жағдайда амплитуда квадратына пропорционал қорытқы интенсивтік те уақытқа байланысты өзгеретін болады, және де осы өзгерістер өте тез өтеді болады. Интенсивтіктің тез өзгерісін сезетіндей қабылдағыштың болмауынан біз интенсивтіктің қайсыбір орташа мәнін тіркеуге мәжбүр боламыз; бұл айнымалы токпен қоректенетін электр лампысының жарықтылығындағы тербелістерді ілесе алмай қайсыбір тұрақты жарықтылықты тіркейтін көзге ұқсас.

Қорытқы тербеліс интенсивтігінің қайсыбір уақыт аралығындағы орташа мәнін есептейік:

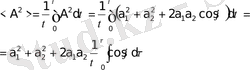
мұндағы . Егер бақылау уақыты ішінде өзгеріссіз қалатын болса (бұл уақыт қабылдағыш аспаптың инерттігіне сәйкес таңдалып алыну тиіс), онда

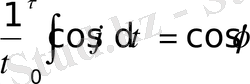демек 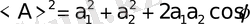, яғни .

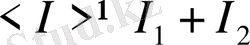Егер тербелістер кездейсоқ үзілетін болса, немесе орташалау уақыты ішінде бұлардың фазалары бейберекет өзгеретін болса, онда

сонда , яғни 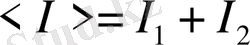болады.

Сонымен периодтары бірдей екі тербеліс қосылғанда мынадай екі жағдай байқалады:

бақылау үшін жеткіліктіуақыты ішінде екі тербелістің фазалар айырымы тұрақты болып қалады () . Мұндай аталады. Когерентті тербелістер қосылғанда қорытқы тербеліс интенсивтігі бастапқы тербелістердің интенсивтіктері қосындысынан өзгеше болады. Бұл құбылыстербелістердің интерференциясыдеп аталады;
уақыт ішінде фазалар айырымы бейберекет түрде өзгереді. Мұндай тербелістер когерентті болмайды да тербелістердің қорытқы интенсивтігі бастапқы тербелістердің интенсивтерінің қосындысына тең болады. Когерентті емес тербелістер қосылғанда интерференция байқалмайды.

Қосылатын тербеліс саны көп болғанда қорытқы амплитуда былай анықталады

(4)

Когерентті тербелістер үшін фазалардың айырмалары берілген нүктеде нақты және тұрақты мәнге ие болады да (4) өрнекке сәйкес қосынды интенсивтік жеке тербелістердің интенсивтіктерінің 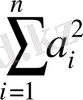қосындысынан үлкен де, кіші де бола алады. Амплитудалар бірдей болған жағдайда барлық тербелістер бірдей фазада келетін нүктелердегі интенсивтік

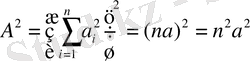болады,

яғни интенсивтіктің шұғыл өсуі ( 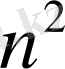есе) байқалады. Басқа нүктелерде интенсивтіктер өзара бірін-бірі өшіреді. Интерференция салдарынан кеңістікте тербелістердің интенсивтігі (энергиясы) қайта үлестіріледі.

Егер тербелістер когерентті болмаса, яғни бір-бірінен тәуелсіз өтетін болса, онда бұлардың фазалары 0-ден -ге дейінгі кездейсоқ мәндер қабылдайды, ал 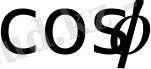бірдей ықтималдықпен оң да, теріс те (+1-ден -1-ге дейінгі) мәндер қабылдайды. Осы жағдайда (4) өрнегіндегі екінші қосындының орташа мәні нөлге тең болады. Сондықтан интенсивтіктің орташа мәні үшін мынаны жазуға болады

яғни қорытқы интенсивтік жеке тербеліс интенсивтерінің қосындысына тең болады.

Сонымен, кез-келген екі гармоникалық тербеліс әрқашан когерентті. Гармоникалық тербелістер интерференциялануға қабылетті монохромат толқындарды туғызады. Толқын ұзындықтары бірдей толқындардың интерференциялану шарты-бұлардың когеренттігі, яғни бақылау үшін жеткілікті уақыт ішінде фазалар айырымының өзгеріссіз сақталуы болып табылады.

Ескеретін нәрсе, “когерентті” және “когерентті емес” терминдері іс жүзінде ешқашан іске аспайтын идеал (мінсіз) күйлерді бейнелейді. Жиіліктері бірдей монохромат толқындар, яғни толқындардың шексіз ұзын цугтары ғана анық когерентті болады. Бейкогеренттік, яғни фазалардың статистикалық мағынада тіптен қалай болса солай өзгеруі де сирек кездеседі: екі жарық шоғы шын мәнінде тәуелсіз болады.

Когерентті толқындардың интерференцияға қабылетті болуы осы толқындар жететін кез-келген нүктеде когеренттік тербелістердің іске асатындығын көрсетеді. Егер толқындардың бағдары мен поляризациясы тербелістер өзара бағыттас болатындай болса, онда толқындар интерференцияланатын болады. Интерференция нәтижесі бақылау жүргізілетін орындағы интерференцияланушы толқындардың фазалар айырымымен анықталады. Фазалардың осы айырымы толқындардың бастапқы фазалар айырымына, және де толқындардың жарық көздерінен бақылау нүктесіне дейінгі жүрген жол айырымына тәуелді болады.

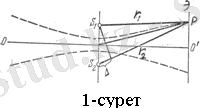
және 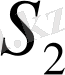әрқайсысы монохромат толқын шығаратын жарық көзі болсын (1-сурет) . Толқындар жазық және қалқадағы (экрандағы) бақылау нүктесінде бұлардың амплитудалары бірдей деп ұйғарайық. Сонда бірінші және екінші толқындардың нүктесінде туғызатын тербелістері мына түрде өрнектеледі

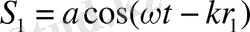және 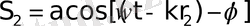, мұндағы ; -бастапқы фазалар айырымы.

нүктесіндегі қорытқы тербеліс мына түрде болады

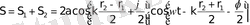(5)

мұндағы

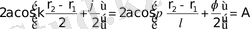
қорытқы тербеліс амплитудасы.

Бақылау нүктесіндегі тербеліс интенсивтігі амплитуда квадратына пропорционал

(6)

Когерент толқындар үшін тұрақты, демек, нүктесіндегі жарық интенсивтігі 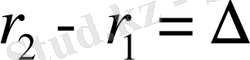қашықтықтарының айырымына ғана тәуелді; -шамасы жол айырымы деп аталады. Жол айырымы болуы себепті, осы екі толқынның бастапқы фазалары бірдей болған жағдайда да, осы толқындар кездесетін (түйісетін) нүктеде бұлардың туғызатын тербелістерінің фазалар айырымы болады.

Жол айырымы себепші болатын фазалар айырымы мынаған тең

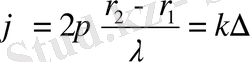. (7)

(7) өрнегін зерттеу арқылы жол айырымы мәндері қандай болғанда максимум және минимум интенсивтік байқалатындығын табамыз. Егер бастапқы фазалар бірдей болса ( ), болған жағдайда тербелістер фазалары бойынша дәл келеді де интенсивтік максимум мәніне жетеді. 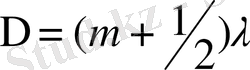болған жағдайда, тербелістер қарама-қарсы фазада болады да қорытқы интенсивтік минимум болады: . саны интерференция реті деп аталады, 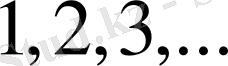мәндер қабылдайды.

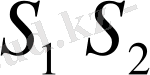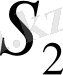Бірдей амплитудалармен сипатталатын және шартын қанағаттандыратын кеңістік нүктелерінің геометриялық орны осі бар айналу гиперболоидының бетін береді (1-сурет) . және нүктелері оның фокустары болады. Айналу гиперболоидтарының біреуінің сурет жазықтығымен қимасы пунктирмен көрсетілген. сызығымен кескінделген ортаңғы жазықтық интенсивтігі максимум жазықтықты сипаттайды.

Интенсивтіктің осы баяндалған үлестірілуі бастапқы фазалар айырымы нөлге тең екі когерент толқынның интерференциясы нәтижесінде алынған интерференциялық көрінісі (суреті) болып табылады.

Когерент емес толқындар үшін әрбір мәніне өзінің интерференциялық суреті сәйкес келеді және ол уақыттың өтуіне байланысты басқа суретке алмасады. Егер осындай алмасу жеткілікті тез өтетін болса, онда біз лездік интерференциялық суреттерді бақылай алмаймыз да, интенсивтіктің біркелкі үлестірілуіне сәйкес келетін қайсыбір орташаланған күйді қабылдайтын боламыз

1. 2. Жарық интерференциясын бақылау әдістері

Егер тәуелсіз екі жарық көзі немесе жарық шығарып тұрған дененің әртүрлі екі бөлігі кеңістіктің бір аймағына жарық толқындарын жіберетін болса, онда интерференция байқалмайды. Интерференциялық суреттің болмауы жарық көздері когерент емес толқындарды жіберетіндігін ғана көрсетуі мүмкін. Бұл жарық көздері шығаратын жарықтың монохромат еместігімен пара-пар, өйткені екі монохромат толқын әрқашан когерентті.

Жарық толқындарының монохромат еместігінің (когерент еместігін) физикалық себебі атомдық процестердің өту ерекшелігіне байланысты. Жарық шығарып тұрған дененің сәулесі зат құрамына кіретін атомдар шығаратын толқындардан құралады. Тәуелсіз екі жарық көзінде біз әрқашан атомдардың бір-бірімен байланыспаған сәуле шығаруымен істес боламыз. Жеке атомның сәуле шығару процесі өте қысқа уақытқа созылады ( 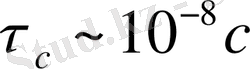), бұдан кейін ол сәуле шығару түріндегі энергия шығыны салдарынан да, қоршаған атомдармен әсерлесуі нәтижесінде де үзіледі. уақыты ішінде атом белгілі ұзындығы бар толқын цугын шығарып үлгереді. Мәселен, жарық жиілігі 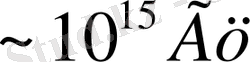болған жағдайда осындай цуг 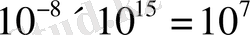толқын ұзындығын қамтиды, яғни осындай цугтың монохроматтығы өте жоғары болады. Сәуле шығаруы тоқтағаннан кейін атомның сәуле шығаруы қайтадан басталуы мүмкін, бірақ та толқындардың жаңа цугының фазасы оның алдындағы цуг фазасымен байланысы болмайды. Сондықтан осындай тәуелсіз екі атомның сәулелері фазаларының айырымы әрқашан сәуле шығарудың жаңа актысы басталған кезде өзгеретін болады.

Сонымен, жарық көзінде өтетін бірқатар физикалық процестер шығарылатын толқынның фазасы мен амплитудасын тұрақты деп санауға болатын ең кіші уақыт аралығын анықтайды. Осы уақыт аралығы когеренттік уақыты ( ) деп аталады, ол шамамен деп бағаланады. Когеренттік уақытын білу арқылы өте маңызды басқа физикалық шаманы- когеренттік ұзындығын бағалауға болады; ол-толқынның фазасы мен амплитудасы орташа алғанда тұрақты болып қалатын уақыт ішінде толқынның таралатын 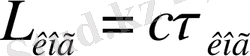қашықтығы.

Сірә, -тің қабылданған бағалануы жағдайында оптикадағы когеренттік ұзындығы 3-30 см болады. Кейбір дербес жағдайларда толқын цугы ұзындығымен ( ) дәл келуі мүмкін.

Осы айтылғандардан кәдімгі жарық көздері көмегімен интерференцияны алудың мүмкін еместігі жайында қорытынды жасауға болады. Осыған байланысты интерференциялық құбылыстар байқалатындай жағдайларды жасауға бола ма, және кәдімгі когерентті емес жарық көздерін пайдаланып өзара когерентті толқындарды алуға бола ма-деген сұрақ өзінен өзі туады. Осы сұраққа жауап беруге тырысайық.

Бір жарық көзі кеңістіктің 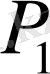және 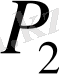әртүрлі нүктелерінде туғызатын тербелістерді қарастырайық. Егер тәжірибенің қандай да бір шарттары орындалатын жағдайда осы тербелістер когерентті болып шықса, онда бұларды қайтадан бір нүктеге тоғыстыру амалын табуға болады. Сонда осы нүктеде сірә интерференция байқалуы тиіс.

Алдымен нүктелік жарық көзімен, яғни сызықтық мөлшері оның шығаратын жарығының толқын ұзындығынан едәуір кіші болатын жарық көзін пайдаланамыз. Осы шектеудің ендірілуі сәуле шығарушы екі атом үшін қосымша жол айырымын ескермеуге мүмкіндік береді де, кез-келген нүкте үшін 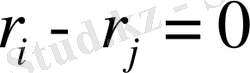деп алуға болады. Зерттелетін сәулені бір атомның шығаратын сәулесімен пара-пар, бірақ толқын фазасы мен амплитудасы когеренттік уақыты ішінде ғана тұрақты деп санауға болады.

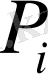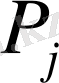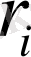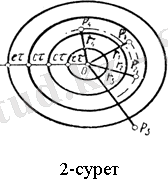
Нүктелік көзді нүктесіне орналастырамыз, және нүктелеріне дейінгі қашықтықтарды және 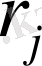арқылы белгілейміз (2-сурет) . Мұнда бірнеше жағдай болуы мүмкін:

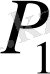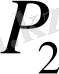1) және нүктелері нүктелік көзден бірдей ( ) қашықтықта орналасады. Бұл нүктелер бір цуг аумағында болады, яғни бұлардағы тербелістер әрқашан когерентті.

2) 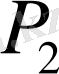және екі нүктенің орналасуындағы айырмашылық орындалатындай болады. Осындай нүктелер кез-келген уақыт мезетінде әртүрлі толқын цугтарына жататын болады, яғни бұлардағы тербелістер когерентті емес;

3) және нүктелері 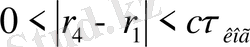болатындай орналасқан. Мұндай тербелістер жарым-жартылай когеренттік деп аталады, бұлар да орнықты интерференциялық суретті бақылауға мүмкіндік береді.

Демек, жарық көзі нүктелік болғанда, жол айрымы когеренттік ұзындығы аумағында жататын жағдайда, интерференцияны бақылауға болады. Бұл әйтеуір бір амалмен толқындардың екі жүйесін алып, бұдан кейін оларды кеңістіктің қандай да бір нүктесіне келтіру қажет екендігін білдіреді. Егер жол айырымы үшін 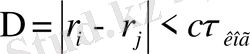шарты орындалатын болса, онда интерференция бақылануы тиіс.

Оптикада толқындардың екі жүйесін алу үшін шағылу және сыну заңдарына негізделген әртүрлі қондырғылар қолданылады. Сонда бір жарық көзі орнына екі шын, немесе шын және жорымал немесе екі жорымал жарық көзін алуға болады да осылар арқылы интерференция бақыланады. Осы жарық көздеріндегі айырмашылық мардымсыз, өйткені шын жарық көзінен шығарылған толқын тиісті оптикалық құрылғы көмегімен қайсыбір аймақта интерференцияланатын екі жарық толқынына бөлінеді. Ал жорымал кескіндерді пайдалану интерференцияны бақылауға мүмкіндік беретін сәулелердің қабаттасу аймағын анықтаудың ыңғайлы амалы ғана болады. Интерференция құбылысын бақылауды мүмкін ететін әртүрлі бірнеше сұлба (схема) бар. Бұлардың кейбіреулерін қарастырайық.

1. 3. Толқындық шепті бөлу арқылы когерентті шоқтарды алу әдістері

Юнг әдісі. Жарықтың интерференция құбылысын бірінші бақылаған және оны дұрыс түсіндірген Т. Юнг болды (1802) . Юнг тәжірибесінде (3-сурет) жарық көзі-жарықтандырылған 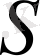саңылауы, бұдан шыққан жарық толқынының әртүрлі бөліктері және жіңішке саңылауларына түсіп, бұларды жарықтандырады. Жарық және 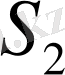кіші тесіктерден өтіп, дифракция нәтижесінде бастапқы бағытынан ауытқиды. Сондықтан толқынның екі бөлігі қабаттасады да, интерференцияланады. Юнг тәжірибесінде интерференцияны бақылау үшін саңылаулар ені өте кішкене болуы тиіс. Енінің мөлшері өте кіші болғанда ғана саңылауынан кейін сфераның бөлігі болып табылатын дұрыс толқындық шеп пайда болады. Бұл және 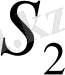саңылауларындағы тербелістердің фазалары бірдей болуын қамтамасыз етеді. 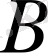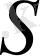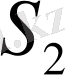Тәжірибе жүргізгенде және арасы 2 м болғанда, саңылауының ені ~0, 3 мм, ал және арасы 1 мм-ден аспауы керек.

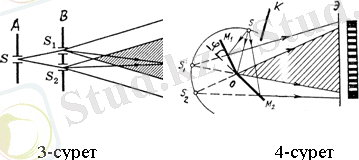
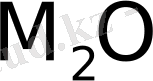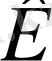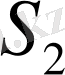Френельдің қос айнасы . Френель когерентті екі жарық көздері ретінде бір жарық көзінің екі жазық айнадағы кескіндерін пайдалануды ұсынды. және өте кішкене -бұрышпен көлбете орнатылған жазық айналар, -монохромат жарық көзі; -ден шыққан сәулелер экранға тікелей түспеуі үшін қалқа қойылған (4-сурет) . және -жарық көзінің жорымал кескіндері. 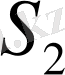Сонда жазық айналардан шағылған жарық толқындарын осы және жорымал кескіндерден шыққан деп қарауға болады. Бұлар когерентті жарық толқындары болып табылады. Өйткені олар, дұрысында, бір жарық көзінен шығып, қосайнадан шағылып, екі айрылған жарық толқындары. Бұлар берілген нүктеге әртүрлі жол жүріп келеді. Басқаша айтқанда алынған нүктеге келген толқындардың белгілі жол айырмасы болады. Сондықтан осы толқындар қосылысқан аймақта интерференциялық кескін байқалады. Френель тәжірибесінде жарық көзі айналар құрайтын қырына параллель жіңішке саңылау түрінде алынады. Осы интерференциялық максимумдар параллель жолақтар түрінде болады.

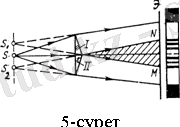
Френель қос призмасы. Френель сыну құбылысын пайдаланып та бір жарық көзінен шыққан жарықты екі шоққа айырып когерентті шоқтар алып, олардың интерференциясын бақылады (5-сурет) . 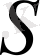жарық көзінен шыққан жарық төбесіндегі бұрышы 180 ⁰ -қа жақын қос призмадан өтеді. Жарық көзі ретінде бипризманың (табандары тиістіріліп орнатылған призмалар) сындыру қырына параллель орнатылған жарықтандырылған тар саңылау алынады Қос призма жарық шоқтарын қарама-қарсы бағытта бұрады, сөйтіп екі жорымал когерентті және жарық көздері пайда болады. Бұлардан шыққан жарық шоқтары бірімен-бірі қосылысып интерференциялық жолақтар береді.

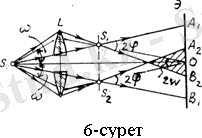
Бийе қос линзасы. Бұл интерференциялық тәжірибе диаметрі бойынша қақ бөлінген линза көмегімен іске асырылады (6-сурет) . Линзаның екі жартысы бір-бірінен аздаған шамаға ажыратылады да, бұлардың көмегімен жарық көзінің және шын кескіні алынады. Жартылай линзалардың арасындағы қуыс қалқамен жабылады. Интерференциялық көрініс және -ден шығатын жарық шоқтары қабаттасатын аймақта пайда болады.

Интерференциялық сұлбалардың (схемалардың) кейбір сипаттамаларын енгізейік. Өйткені Бийе тәжірибесінде бұлардың ең маңызды жақтары айқын көрінеді.

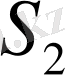және жарық көзінен шығатын сәулелер арасындағы 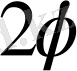бұрышының максимум мәні және шартына сәйкес келеді, яғни қалқанының шексіздікке орналасуына сәйкес келеді. 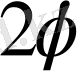апертура шамасы жарықталудың қайта үлестірілуі өтетін интерференциялық жолақтар пайда болатын-интерференция өрісінің бұрыштық мөлшерін анықтайды.

-тен экранның орталық нүктесі -ға келетін сәулелер арасындағы бұрышы нүктесіндегі интерференциялық эффекті анықтайтын сәулелердің ажыратылу бұрышын сипаттайды. Осы бұрыш интерференциялық өрістің кез-келген басқа нүктесі үшін де сол мәнін сақтайды. бұрышы интерференция апертурасы деп аталады. Интерференция өрісінде оған сәулелердің түйісу бұрышы сәйкес келеді, мұның шамасы бұрышымен кескіндерді тұрғызу ережелерімен байланысқан.

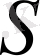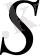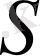Ллойд айнасы. жарық көзінен кіші бұрышпен жинақсыз жарық шағылдырғыш бетке-жазық металл айнаға түседі (7-сурет) . Айна жазықтығына перпендикуляр орнатылған экранда интерференция бақыланады. Осы жағдайда және оның айнадағы жорымал кескіні когерентті жарық көздері болады. Металл айнадан шағылғанда толқын фазасы -ге өзгеретіндіктен, және синфазалы емес, қарама-қарсы фазаларда болады. Сонымен, Ллойд сұлбасында (схемасында) интерференциялық сурет түгелдей таза геометриялық есептеумен салыстырғанда жарты жолаққа ығысқан болады.