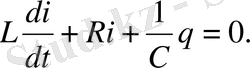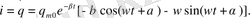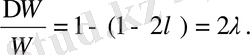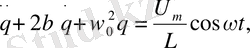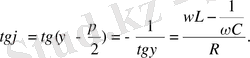Физикалық процестерді математикалық модельдеу және мектептегі оқытуға арналған демонстрациялық компьютерлік бағдарламалар


Мазмұны
Кіріспе . . . 3
І. Зерттелетін процестердің физикалық негіздері . . . 5
1. 1. Механикалық тербелістер . . . . 5
1. 2. Электр тербелістері7
1. 3. Заттардың α-бөлшектерін шашыратуы. Резерфорд тәжірибесі…. 15
ІІ. Физикалық процестерді зерттеудің математикалық әдістері……. 22
2. 1. Қарапайым дифференциалдық теңдеулерді жуықтап
шешу әдістері. Эйлер әдісі. . 22
2. 2. Рунге-Кутта әдісі. 24
2. 3. Ақырлы айырымдар әдісі. . 31
ІІІ. Компьютерді оқу процесінде қолдану . . . 33
3. 1. Компьютердің физиканы оқытудағы ролі. . . 33
3. 2. Компьютерді оқытуда қолдану әдістері. . 34
3. 3. Физикалық процестерді компьютерде моделдеу35
3. 4. Серіппелі маятниктің тербелісін моделдеу . . . 35
3. 5. Электрлік тербелмелі контурдағы өшетін
тербелістерді моделдеу . . . 44
3. 6. Альфа-бөлшектердің шашырауы бойынша Резерфорд
тәжірибелерін моделдеу . . . 48
3. 7. Өзара байланысты екі шаманың сызықтық
тәуелділігін моделдеу . . . 52
Қорытынды . . . 59
Пайдаланылған әдебиеттер . . . 60
Қосымшалар . . . 62
Кіріспе
Дипломдық жұмыстың тақырыбының өзектілігі. Дипломдық жұмыс физиканы орта мектептерде оқыту барысында қолданатын демонстрациялық бағдарламаларды құрастыруға және оның қолдану әдістемесін жасауға арналған.
Заманауи мектептердің компьютерлермен және интерактивті тақталармен толық қамтылуы мұғалім компьютермен жұмыс істеу жағынан психологиялық және кәсіптік дайын болмаса білім беруді өзгеріске алып келмейді.
Қазіргі уақытта есептеу техникасын физикалық зерттеулерде қолданудан үлкен тәжірибе жинақталған, негізгі физикалық мәселелерді шешудің жалпы әдістемелік жолы жасалған, сондайақ жалпы физикамен және теориялық физикамен қатар заманауи физиканың құрамдас бөлігі болатын физика бойынша білім стандартына кіретін жаңа пән-компьютерлік физика пайда болды деп айтуға болады.
Компьютерлік физиканың негізгі зерттеу әдісі - теориялық базасы ретінде математикалық моделдеу, ал эксперименттік базасы ретінде ЭЕМ қызмет ететін компьютерлік эксперимент болып табылады [2] .
Компьютерлік модельдеу теориялық физика, сандық талдау және бағдарламалау пәндерін интеграциялайды.
Бүгінгі күнде физиканы оқытуда көптеген маңызды физикалық құбылыстар мен тәжірибелерді, олардың қиындығына байланысты құралдардың көмегімен демонстрациялық түрде көрсете алмайды. Оларды түсіндіру үшін мұғалімнен үлкен “бейнелеу мүмкіндігін” талап етеді. Міне, сондықтанда осы сияқты күрделі процестерді модельдеу үшін компьютерлік бағдарламалар жасау тенденциясы пайда болды [1-7] . Күрделі демонстрациялың компьютерлік модельдері жасалса, мұғалім бастапқы мәндерді алдын-ала дайындап, материалдарды түсіндіру барысында процестің дамуының мүмкін болар варианттарын және оларға сәйкес графиктерді эксперименттік қондырғының компьютердегі моделінің көмегімен көп уақыт жұмсамай-ақ демонстрациялауға болады.
Бұдан бөлек мұндай бағдарламаларды күрделі деңгейлі әр түрлі қосымша тапсырмасы бар практикумдарда қолдануға болады.
Дипломдық жұмыстың мақсаты:
- демонстрациялық компьютерлік бағдарламаларды жасауға қажетті аналитикалық шешімдерді алу үшін моделі жасалатын физикалық процестерді зерттеу. Сандық әдістер негізінде алгоритмдер құру;
- Алынған шешімдер негізінде демонстрациялық бағдарламалар жасау және лабораториялық жұмыстар құрастыру;
- Құрастырылған лабораториялық жұмыстарды апробациядан өткізу.
Дипломдық жұмыс нәтижелерінің ғылыми жаңалығы:
Жұмыста алғаш рет:
- “Өзара байланысты екі шаманың сызықтық тәуелдлігін моделдеу”, Серіппелі маятниктің тербелісін моделдеу”, “Электрлік тербелмелі контурдағы өшетін тербелістерді моделдеу”, “Альфа-бөлшектердің шашырауы бойынша Резерфорд тәжірибелерін моделдеу” тақырыптары бойынша 11-сыныпқа араналған лабораториялық жұмыстар құрастырылды
Ғылыми және практикалық құндылығы:
Жұмыста зерттелетін физикалық процестерге теориялық талдау жасалып және бір қатар физикалық эксперименттерді моделдеуші бағдарламалар құрастырылған.
Дипломдық жұмыстағы теориялық нәтижелер мен компьютерлік бағдарламалар әр түрлі оқу орындарында физиканы оқыту процесінде және берілген материалды өзбетінше оқып үйренуде қолдануға болады.
Автордың үлесі:
Жұмыста, қорғауға ұсынылатын және жетекшімен бірге орындалған нәтижелерде автор, есептің қойылуына, зерттеу әдісін таңдауда, теориялық талдауларға, нәтижелерді тарату мен интеграциялау әдістеріне өз үлесін қосты.
І. Зерттелетін процестердің физикалық негіздері
1. 1. Механикалық тербелістер
Тербелістер туралы жалпы мәліметтер
Тербелістер деп белгілі бір дәрежеде қайталағыштығымен айқындалатын процестерді айтады. Мысалы, сағат маятнигінің тербелуі, ішектің немесе камертон таяқшасының тербелісі, радиоқабылдағыш контурының конденсатор астарларындағы кернеу және т. б. осындай қайталағыштық қасиетке ие болады.
Қайталанатын процестің физикалық табиғатына байланысты тербелістер: механикалық, электромагниттік, электромеханикалық және т. б. түрге бөлінеді. Бұл жерде механикалық тербелісті қарастырамыз.
Тербелмелі жүйеге жасалатын әсердің сипатына қарай еркін тербелістер, еріксіз тербелістер автотербелістер және параметрлік тербелістер болып ажыратылады.
Еркін тербелістер деп қозғалысқа келтірілгеннен кейін немесе орнықты қалпынан шығарылғаннан соң өзімен-өзі қалатын жүйеде өтетін тербелістерді айтады.
Еріксіз тербелістер деп тербелмелі жүйеге әлсін-әлі өзгеріп отыратын сыртқы күштің әсеріне кез болатын тербелістерді айтады.
Еріксіз тербелістер сияқты автотербелістер де тербелмелі жүйеге сыртқы күштердің әсер етуімен жүреді; алйда бұл әсерлер жүзеге асатын уақыт мезетінде тербелмелі жүйенің өзі белгілейді-сыртқы әсерлерді жүйенің өзі басқарады. Жоғары көтерілген гирдің немесе бұралған серіппенің энергиясы есебінен маятнигі түрткі алатын сағат осыған мысал бола алады.
Параметрлік тербелістер кезінде сыртқы әсер салдарынан жүйеде қандай да болсын параметрі, мысалы, тербеліс жасап тұрған шарик ілінген жіптің ұзындығы, периодты түрде өзгереді.
Гармониялық тербелістер, яғни тербелетін шама уақыт бойынша синус не косинус заңына сәйкес өзгеретін тербелістер қарапайым тербелістер қатарына жатады. Бұл тербелістер мына себептерден аса маңызды деп саналады: біріншіден табиғаттағы және техникадағы тербелістер көбінесе гармониялық тербелістерге жақын сипатта болады, және екіншіден басқа түрдегі периодты процестерді бірнеше гармониялық тербелістердің қосылуы ретінде қарастыруға болады.
Гармониялық тербелістер .
Серіппеге ілінген, массасы m шариктен тұратын жүйені қарастырайық (cурет) . Тепе-теңдік күйінде mg күші k∆l 0 cерпімділік күшімен теңгеріледі:
mg= k∆l 0 (1. 1)
Шариктің тепе-теңдік қалпынан ығысуын х координатасымен сипаттаймыз, әрі осін вертикаль бойынша төмен бағыттаймыз, ал осьтің нолін шариктің тепе-теңдік қалпымен үйлестіреміз.
Егер шарикті тепе-теңдіктен х-қа тең қашықтыққа ығыстырсақ, онда серіппенің ұзаруы ∆l 0 + х шамасына тең болады және қорытқы күштің х осіне
1-сурет.
проекциясы (бұл проекцияның жай ғана f әрпімен белгілейік) мынадай мән қабылдайды:
f=mg-k(∆l 0 +x) .
(1. 1) формуласындағы тепе-теңдік шартын ескере отырып, төмендегіні аламыз:
f=-kx. (1. 2)
(1. 2) формуласындағы ығысу мен күштің бағыттары қарама-қарсы екендігін білдіреді: егер шариктің тепе-теңдік қалпынан төмен қарай (х>0) ығысса, күш жоғары (f<0 ) бағытталады, шарик жоғары қарай (х<0) ығысқанда күш төмен (f>0) бағытталады. Сонымен f күшінің төмендегідей қасиеттері бар: 1) ол шариктің тепе-теңдік қалпынан ығысуына пропорционал, 2) ол әр қашанда тепе-теңдік қалпына қарай бағытталған.
Біз қарастырған мысалда (1. 2) күш шынында, өзінің табиғаты бойынша серпімді. Басқа тектегі күштерде де осындай заңдылық байқалуы мүмкін. Табиғатына қарамастан, мұндай күштерді квазисерпімді деп атау келісілген.
Шарикке арналған Ньютонның екінші заңы былай жазылады:
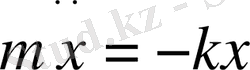
Бұл теңдеуді төмендегідей етіп түрлендірейік:
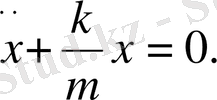 (1. 3)
(1. 3)
х-тағы коэффициент оң. Сондықтан оны мынадай түрде жазуға болады:
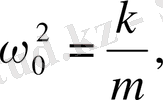 (1. 4)
(1. 4)
(1. 3) өрнегіне (1. 4) -өрнегіндегі белгілеуді қолдана отырып, мынаны аламыз:
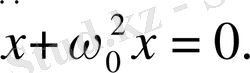 (1. 5)
(1. 5)
 циклдік жиілік.
циклдік жиілік.
Сонымен (1. 2) түріндегі күштің әсерінен болатын шарик қозғалысы екінші реттік біртекті дифференциалдық теңдеулер арқылы зерттеледі.
Бұл гармониялық тербеліс теңдеулерінің шешуі:
х(t
) =
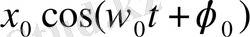 (1. 6)
(1. 6)
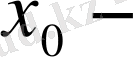 тербеліс амплитудасы,
тербеліс амплитудасы,
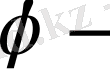 тербелістің бастапқы фазасы.
тербелістің бастапқы фазасы.
Тербеліс кезіндегі жылдамдық:
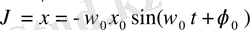 (1. 7)
(1. 7)
 жылдамдық тербелісінің амплитудасы
жылдамдық тербелісінің амплитудасы
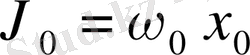 (1. 8)
(1. 8)
Тербелістер кезіндегі үдеу:
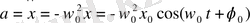 (1. 9)
(1. 9)
 тербеліс үдеуінің амплитудасы
тербеліс үдеуінің амплитудасы
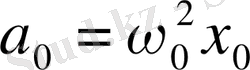 (1. 10)
(1. 10)
1. 2. Электр тербелістері
Актив кедергісі жоқ контурдағы еркін тербелістер
Электр тербелісі индуктивтілігі мен сыйымдылығы бар тізбекте пайда бола алады. Мұндай тізбек т е р б е л і с к о н т у р ы деп аталады. 5, а-суретте актив кедергісі нолгьге тең идеал контурдағы тербеліс процесінің жүйелі кезеңдері кескінделген.
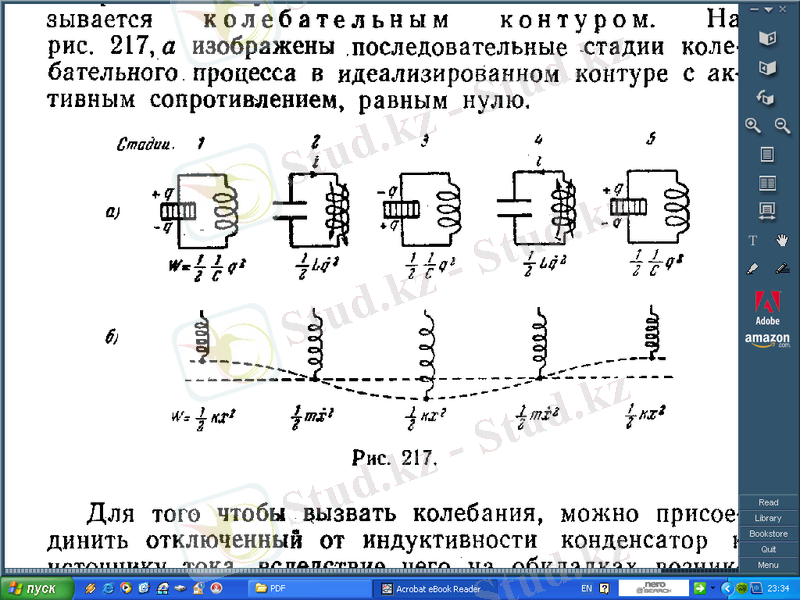
2-сурет.
Тербелісті туғызу үшін индуктивтіліктен ажыратылған конденсаторды ток көзіне қосу керек, осының салдарынан конденсатор астарларында шамасы
q
m
әр атты зарядтар пайда болады (1-кезең) . Астарлар арасында энергиясы
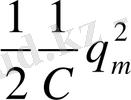 шамасына тең электр өрісі пайда болады. Егер осыдан кейін электр көзін ағытып, конденсаторды индуктивтілікпен тұйықтасақ, сыйымдылық разрядтала бастайды да контур бойымен ток өтетін болады. Нәтижесінде электр өрісінің энергиясы кеми бастайды да, есесіне индуктивтілік арқылы ағып өткен токтан пайда болатын магнит өрісінің өспелі энергиясы туады. Бұл энергия
шамасына тең электр өрісі пайда болады. Егер осыдан кейін электр көзін ағытып, конденсаторды индуктивтілікпен тұйықтасақ, сыйымдылық разрядтала бастайды да контур бойымен ток өтетін болады. Нәтижесінде электр өрісінің энергиясы кеми бастайды да, есесіне индуктивтілік арқылы ағып өткен токтан пайда болатын магнит өрісінің өспелі энергиясы туады. Бұл энергия
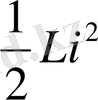 шамасына тең болады.
шамасына тең болады.
Тізбектің актив кедергісі нольге тең болғандықтан, электр өрсінің
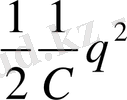 энергиясы мен магнит өрісінің
энергиясы мен магнит өрісінің
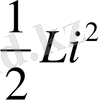 энергиясынан құралған толық энергия конденсатор астарларын қыздыруға жұмсалмастан тұрақты болып қалады. Cондықтан конденсатордағы кернеу, демек, электр өрісінің энергиясы нольге айналған мезетте, магнит өрісінің энергиясы, ендеше, ток та өзінің ең үлкен мәніне жетеді (2 кезең, осы мезеттен бастап ток өздік индукцияның э. қ. күштерінің есебінен ағатын болады) . Әрі қарай ток кеми бастайды, астарлардағы заряд өзінің бастапқы
q
m
шамасына жеткен кезде, ток күші нольге тең болады (3 кезең) . Осыдан кейінгі жерде процестер керісінше өтеді де (4 және 5 кезең), система бастапқы күйіне келеді (5 кезең), сөйтіп, барлық цикл қайтадан қайталай беретін болады. Сипатталған процестің барысында астарлардағы
q
заряд, конденсатордағы
U
кернеу және индуктивтілік арқылы өтетін
і
ток күші периодты түрде өзгеріске (яғни тербеліске) ұшырайды. Тербеліс электр өрісі энергиясы мен магнит өрісі энергиясының өзара айналуымен қосарласа өтеді.
энергиясынан құралған толық энергия конденсатор астарларын қыздыруға жұмсалмастан тұрақты болып қалады. Cондықтан конденсатордағы кернеу, демек, электр өрісінің энергиясы нольге айналған мезетте, магнит өрісінің энергиясы, ендеше, ток та өзінің ең үлкен мәніне жетеді (2 кезең, осы мезеттен бастап ток өздік индукцияның э. қ. күштерінің есебінен ағатын болады) . Әрі қарай ток кеми бастайды, астарлардағы заряд өзінің бастапқы
q
m
шамасына жеткен кезде, ток күші нольге тең болады (3 кезең) . Осыдан кейінгі жерде процестер керісінше өтеді де (4 және 5 кезең), система бастапқы күйіне келеді (5 кезең), сөйтіп, барлық цикл қайтадан қайталай беретін болады. Сипатталған процестің барысында астарлардағы
q
заряд, конденсатордағы
U
кернеу және индуктивтілік арқылы өтетін
і
ток күші периодты түрде өзгеріске (яғни тербеліске) ұшырайды. Тербеліс электр өрісі энергиясы мен магнит өрісі энергиясының өзара айналуымен қосарласа өтеді.
5, б-суретте контурдағы тербеліс серіппелі маятниктің тербелісімен салыстырылған. Конденсатор астарларына түсірілген заряд маятникті сыртқы күштердің әсерімен тепе-теңдік қалпынан шығаруға және оған берілген алғашқы
х
m
ауытқуға сәйкес келеді. Бұл жағдайда серіппенің серпімді деформациясының потенциялық энергиясы пайда болады. 2 кезең маятниктің тепе-теңдік қалпынан өтуіне сәйкес келеді. Осы мезетте квази серпімді күш нольге тең болады да, маятник инерциясы бойынша қозғала береді. Осы уақытта маятник энергиясы толығынан кинетикалық энергияға ауысады да
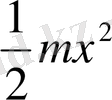 өрнегімен анықталатын болады. Осыдан кейінгі кезеңдерді салыстыруды оқушылардың өздеріне ұсынамыз.
өрнегімен анықталатын болады. Осыдан кейінгі кезеңдерді салыстыруды оқушылардың өздеріне ұсынамыз.
Электр және механикалық тербелістерді салыстырудан
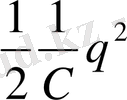 электр өрісі энергиясының серпімді деформацияның потенциялық энергиясына ұқсастығы, ал
электр өрісі энергиясының серпімді деформацияның потенциялық энергиясына ұқсастығы, ал
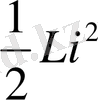 магнит өрісі энергиясының кинетикалық энергияға ұқсастығы шығады. Индуктивтілік
L
-
m
массасының ролін, сыйымдылыққа (1/С) кері шама -серпімділік коэффициенті
k
-ның ролін атқарады. Ақырында,
q
зарядына маятниктің тепе-теңдік қалыптан ығысуы
х
, ал
магнит өрісі энергиясының кинетикалық энергияға ұқсастығы шығады. Индуктивтілік
L
-
m
массасының ролін, сыйымдылыққа (1/С) кері шама -серпімділік коэффициенті
k
-ның ролін атқарады. Ақырында,
q
зарядына маятниктің тепе-теңдік қалыптан ығысуы
х
, ал
 -ток күшіне
-ток күшіне
 жылдамдық сәйкес келеді. Төменде көретініміздей, электр және механикалық тербелістің арасындағы ұқсастық оларды сипаттайтын математикалық теңдеулерге де қолданылады.
жылдамдық сәйкес келеді. Төменде көретініміздей, электр және механикалық тербелістің арасындағы ұқсастық оларды сипаттайтын математикалық теңдеулерге де қолданылады.
Тербеліс кезінде сыртқы кернеу контурға түспейді. Сондықтан
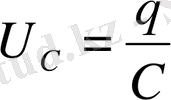 сыйымдылық пен
сыйымдылық пен
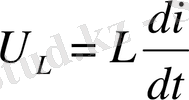 индуктивтілік кернеудің кемуі қосындысы нольге тең болуы тиіс:
индуктивтілік кернеудің кемуі қосындысы нольге тең болуы тиіс:
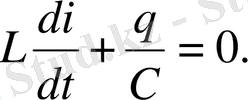
Бұл өрнек
L
-ге бөліп және
 қатынасын
қатынасын
 (
(
 ) арқылы ауыстырып, мына өрнекке келеміз:
) арқылы ауыстырып, мына өрнекке келеміз:
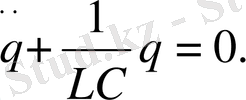 (
1. 11
)
(
1. 11
)
Егер
( 1. 12 )
Белгілеуін енгізсек, (1. 11) теңдеуді механикалық тербелістер жайындағы ілімнен бізге жақсы таныс мынадай түрге келеді:
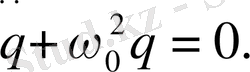 (1. 13)
(1. 13)
Бұл теңдеудің шешуі, біз білетін
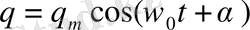 (1. 14)
(1. 14)
функция болып табылады.
Сөйтіп, конденсатор астарларындағы заряд жиілігі (1. 12) өрнегімен анықталатын гармониялық заң бойынша өзгереді. Бұл жиілік контурдың меншікті жиілігі деп аталады. Тербеліс периоды үшін Томсон формуласы деп аталатын өрнекті аламыз:
 (1. 15)
(1. 15)
Конденсатордағы кернеудің зарядтан айырмашылығы 1/С көбейткіштің болуында:
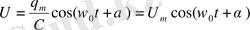 (1. 16)
(1. 16)
(1. 16) функцияны уақыт бойынша дифференциалдап, ток күшіне арналған
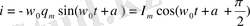 (1. 17)
(1. 17)
өрнегін аламыз:
(1. 14) пен (1. 17) формуланы салыстыра отырып, ток максимал мәніне жеткенінде заряд (сондай-ақ кернеу) нольге айналады, және керісінше болады деп қорытамыз. Заряд пен ток арасындағы сондай қатысты, энергетикалық түсінікті негізге ала отырып, біз бұрын анықтаған болатынбыз.
(1. 16) және (1. 17) формуладан
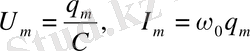
екені шығады.
(1. 12) формуласы бойынша ω 0 -ны ауыстыра отырып, мынаны аламыз:
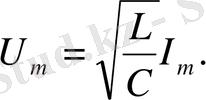 (1. 18)
(1. 18)
Өшетін еркін тербелістер
Кез келген нақты контур актив кедергіге ие болады. Контурда жиналған энергия қоры осы кедергіге бірте-бірте жылуға жұмсалады, осының салдарынан еркін тербелістер өшетін болады. Тербеліс теңдеуін сыйымдылықтағы, индуктивтіктегі және актив кедергідегі кернеу кемуінің қосындысының нольге тең болуынан шығарып алуға болады:
Бұл өрнекті
L
-ге бөліп және
i
-ді
 арқылы, ал
арқылы, ал
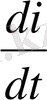 -ні
-ні
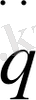 арқылы ауыстырып, мынаны аламыз:
арқылы ауыстырып, мынаны аламыз:
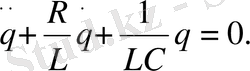 (
1. 19
)
(
1. 19
)
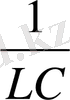 -
нің контурдың
ω
0
меншікті жиілігінің квадратына тең екенін ескеріп және
-
нің контурдың
ω
0
меншікті жиілігінің квадратына тең екенін ескеріп және
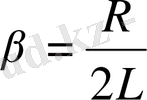 (
1. 20
)
(
1. 20
)
белгілеуін енгізе отырып, (1. 19) теңдеуін мына түрге келтіруге болады:
( 1. 21 )
Соңғы теңдеу өшетін механикалық тербелістің дифференциал теңдеімен дәл келеді.
 шартында, яғни
шартында, яғни
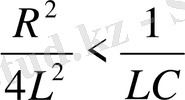 болғанда (1. 22) теңдеудің шешуі мына түрге келеді:
болғанда (1. 22) теңдеудің шешуі мына түрге келеді:
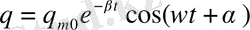 , (1. 22)
, (1. 22)
мұндағы
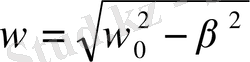 .
ω
0
-ның және
β
-ның мәнін қойып, мынаны табамыз:
.
ω
0
-ның және
β
-ның мәнін қойып, мынаны табамыз:
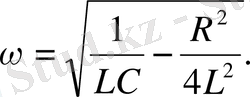 (
1. 23)
(
1. 23)
Сөйтіп, өшетін тербелістің жиілігі ω меншікті жиілігі ω 0 -ден кем болады. R=0 болғанда (1. 23) өрнегі (1. 12) -ге ауысады.
(1. 22) -ті сыйымдылық С-ға бөліп, конденсатордағы кернеуді аламыз:
(1. 24)
Ток күшін табу үшін (1. 22) -ті уақыт бойынша дифференциалдаймыз:
Бұл өрнекті
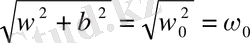 шамасына көбейтіп, бөлгеннен:
шамасына көбейтіп, бөлгеннен:
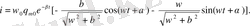
ψ бұрышын анықталған

шарты бойынша енгізе отырып, былай жазуға болады:
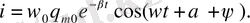 (1. 25)
(1. 25)
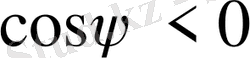 , ал
, ал
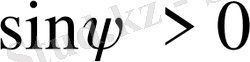 болғандықтан да
болғандықтан да
 . Сөйтіп, контурда актив кедергінің бар болуынан ток фаза бойынша конденсатордағы кернеуден
. Сөйтіп, контурда актив кедергінің бар болуынан ток фаза бойынша конденсатордағы кернеуден
 -ден гөрі (R=0 болғанда озу
-ден гөрі (R=0 болғанда озу
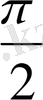 -ні құрайды) озық кетеді.
-ні құрайды) озық кетеді.
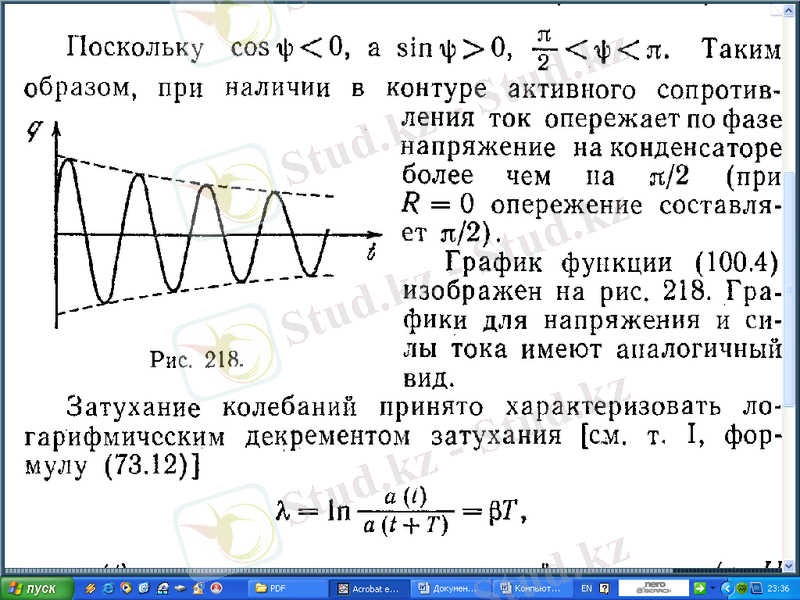
3-cурет.
(1. 22) функцияның графигі 3-суретте кескінделген. Кернеу мен токтың графигі бір-біріне түр жағынан ұқсас болады.
Тербелістің өшуін өшудің логарифмдік декрементімен сипаттау қабылдаған.
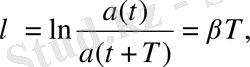
мұндағы а(t) -сәйкес шамалардың ( q, U немесе і ) амплитудалары.
Өшудің логарифмдік декременті амплитудасы е рет кемитін уақыт ішінде жасалған N e тербеліс санына кері шама болады:
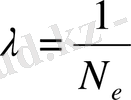
Тербелмелі контурды әрқашан оның мықтылығымен (Q) сипаттайды, бұл өшудің логарифмдік декрементіне кері пропорционал шама ретінде анықталады:
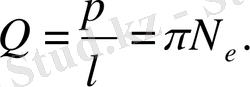 (1. 26)
(1. 26)
(1. 26) теңдеуден контурдың мықтылығы неғұрлым жоғары болса, соғұрлым амплитуда е рет кемігенге дейін тербеліс саны жасалып үлгереді. λ -ның орнына оның βT мәнін алып, мынаны табамыз:
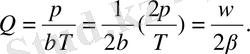
Егер өшу аса үлкен болмаса (
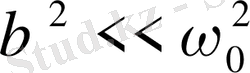 ),
),
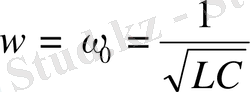 деп ұйғаруға болады. Сонда
деп ұйғаруға болады. Сонда
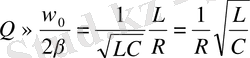
Сөйтіп, өшу баяу болған жағдайда
(1. 27)
Контурдағы ток күшінің амплитудасы е -βt заңы бойынша кемиді. Контурда жинақталған W энергия ток күші амплитудасының квадратына (немесе конденсатордағы кернеу амплитудасының квадратына) пропорционал болады; демек, W е -2βt заңы бойынша кемиді. Период ішінде энергияның салыстырмалы кемуі мынаған тең:
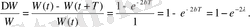
Шамалы өшу кезінде (яғни λ<< 1 орындалғанда) е -2λ -ні 1-2λ арқылы жуықтап ауыстыруға болады:
Бұл өрнектегі λ-ны (1. 26) формуласына сәйкес контурдың Q мықтылығымен ауыстырып, әрі шыққан теңдеуді Q-ға қатысты шешіп, мынаны аламыз:
( 1. 28 )
Сонымен, баяу өшу кезінде контурдың мықтылығы контурда жинақталған энергияның осы тербелісітің бір периоды ішінде кемуіне қатынасына пропорционал болады екен.
Қорытындылай келе
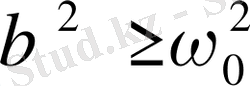 , яғни
, яғни
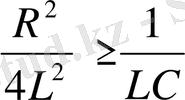 болғанда тербеліс орнына конденсатордың апериодты (периодсыз) разряды жүреді. Тербелмелі процестің апериодты процеске ауысуындағы контурдың кедергісі
кризистік
кедергі деп аталады. Кризистік кедергі
R
k
-нің мәні
болғанда тербеліс орнына конденсатордың апериодты (периодсыз) разряды жүреді. Тербелмелі процестің апериодты процеске ауысуындағы контурдың кедергісі
кризистік
кедергі деп аталады. Кризистік кедергі
R
k
-нің мәні
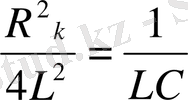 шартымен анықталады, бұдан
шартымен анықталады, бұдан
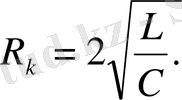 (
1. 29
)
(
1. 29
)
Еріксіз электр тербелістері
Еріксіз тербелісті шығарып алу үшін системаға периодты түрде өзгеріп тұратын сырттай әсер беру керек екен. Электр тербелісі жағдайында, мұны контур элементіне тізбектей қосылған айнымалы э. қ. күшін немесе контурды үзіп жіберіп, жаңа пайда болған контактіге айнымалы U кернеуін беру арқылы іске асыруға болады. Электр және механикалық тербелістердің арасындағы ұқсастықты аяғына дейін жүргізу үшін біз еріксіз электр тербелістерінің теңдеулеріне басқаша түр бере отырып, қарасытрамыз.
Контурдың элементіндегі кернеу кемулерінің қосындысын түсірілген кернеуге теңестіреміз
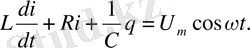
І токтан q зарядына өте отырып, (1. 12) және (1. 20) белгілеулерді пайдаланып, мына теңдеуі аламыз:
Бұл еріксіз механикалық тербелістің дифференциал теңдеуімен бірдей. Осы теңдеудің дербес шешуі мына түрде болады:
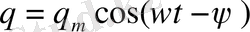 , (1. 30)
, (1. 30)
мұндағы
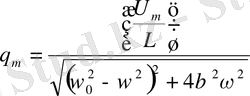 (1. 31)
(1. 31)
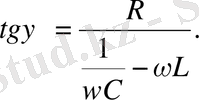 (1. 32)
(1. 32)
Егер (1. 30) дербес шешуге сәйкес біртекті теңдеудің жалпы шешуін қоссақ, жалпы шешуді аламыз. Бұл шешу алдынғы параграфта алынған болатын, мұнда экспоненциал е -βt көбейткіш бар, сондықтан тербеліс басынан саналатын жеткілікті уақыт аз болып шығады, оны елемеуге болады. Демек, орныққан еріксіз тербелісіміз (1. 30) функциямен сипатталады екен. Алдыңғы тарауда тек орныққан ток пен кернеудің ғана қарастырылғанын ескертелік.
Заряд q -ды сыйымдылық С -ге бөліп, конденсатордағы кернеуді аламыз:
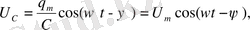
мұндағы
(1. 33)
(1. 30) функцияны t бойынша дифференциалдай отырып, контурда орныққан токты табамыз:
(1. 34)
Ток амплитудасының өрнегімен сәйкес келетін мәні төмендегіше болады:
(1. 35)
(1. 35) -ке ϕ=ψ−π/2 белгілеулерін енгізе отырып, біз (1. 32) -ге сәйкес мынаны аламыз:
q заряды үшін резонанстық жиілік пен конденсатордағы U С кернеу мынаған тең:
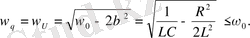 (1. 36)
(1. 36)
4-суретте U С үшін резонанстық қисықтық кескінделген (q-дың резонанстық қисықтығы да дәл осындай) . Бұлар механикалық тербелістер үшін алынған резонанстық қисықтармен ұқсас. ω→0 болғанда резонанстық
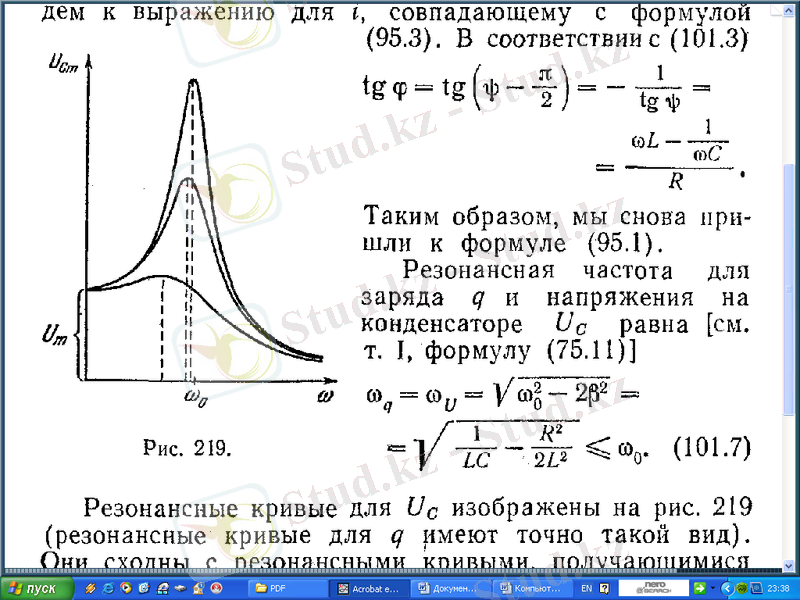
4-сурет.
қисықтар
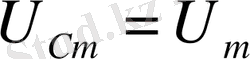 -ға-конденсаторды қосқанда, онда пайда болатын кернеуге ұмтылады. Неғұрлым β=R/2L аз болса, яғни неғұрлым конденсатордағы актив кедергі аз, индуктивтілік көп болса, резонанс кезінде максимум соғұрлым жоғары, әрі сүйірлеу болып келеді.
-ға-конденсаторды қосқанда, онда пайда болатын кернеуге ұмтылады. Неғұрлым β=R/2L аз болса, яғни неғұрлым конденсатордағы актив кедергі аз, индуктивтілік көп болса, резонанс кезінде максимум соғұрлым жоғары, әрі сүйірлеу болып келеді.
Ток күші үшін резонанстық қисықтар 5-суретте кескінделген. Бұлар механикалық тербеліс кезіндегі жылдамдықтың резонанстық қисықтығына сәйкес келеді. (1. 35) ток күшінің амплитудасы ωL-1/ωC=0 болғанда максимал мәнге ие болады. Демек, ток күшінің резонанстық жиілігі контурдың меншікті жиілігі ω 0 -ге дәл келеді. І m осіндегі резонанстық қисықпен қиылысатын кесінді нольге тең-кернеу тұрақты болғанда конденсаторы бар тізбектегі орныққан ток ағып өте алмайды.
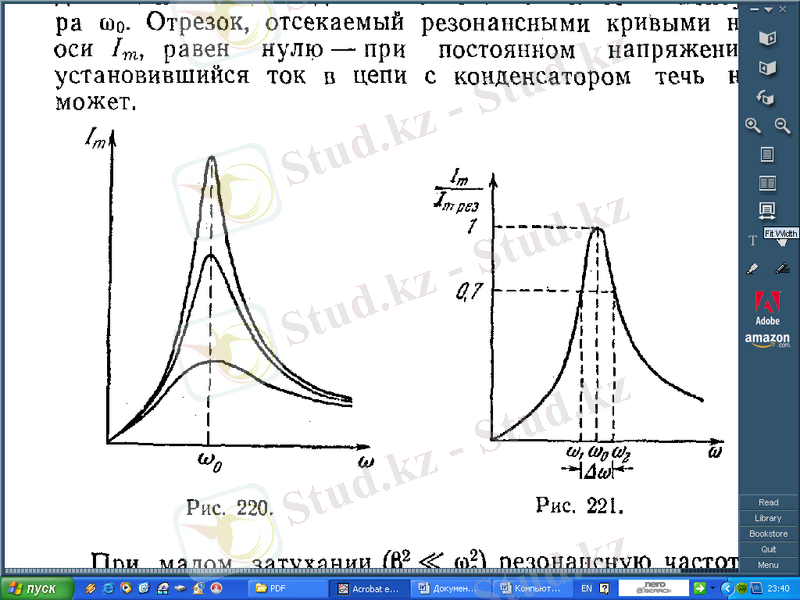
5-cурет.
Өшу аз болғанда (
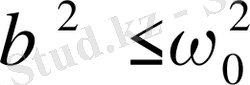 ) кернеудің (1. 38) резонанстық жиілігін ω
0
-ге тең деп ұйғаруға болады:
) кернеудің (1. 38) резонанстық жиілігін ω
0
-ге тең деп ұйғаруға болады:
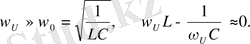
( 1. 33 ) формуласы бойынша U cmрез резонанс кезінде конденсатордағы кернеу амплитудасының U m сыртқы кернеу амплитудасына қатынасы бұл жағдайда мынаған тең болады:
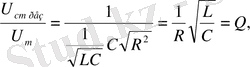
мұндағы Q -контурдың мықтылығы.
Контурдың мықтылығы резонанстық қисықтықтың сүйірлігін де сипаттайды.
1. 3. Заттардың α-бөлшектерін шашыратуы.
Резерфорд тәжірибесі
Кіріспеде айтып өткендей, атом құрылымы туралы дұрыс ұғымға ғалымдар бірден келек қойған жоқ. Жүргізілген зерттеулердің нәтижесінде 1900 жылы электрон барлық атомдардың құрамында болатыны анықталды. Ал олай болса, атом массасы тек қана электрон массасымен анықтала ма, алде атом ішінде электронның теріс зарядын бейтараптайтын заряд орналасқан ба? Міне осы және басқа сұрақтарға жауап беру үшін әр түрлі елдердің ғалымдары атом моделін ұсынды. Модель белгілі бір зерттелетін физикалық дененің, құбылыстың немесе денелер, құбылыстар жүйесінің ой түсінігі арқылы немесе материалды түрде жасалған шартты үлгісі. Модель жасау түсініксізнемесе аз зерттелген денені, құбылысты бұрыннан жақсы мәлім әрі зерттелген денелермен, құбылыстармен осы құбылыстың, дененің моделі ретінде салыстыру жолымен зерттеуге немесе түсіндіруге мүмкіндік береді.
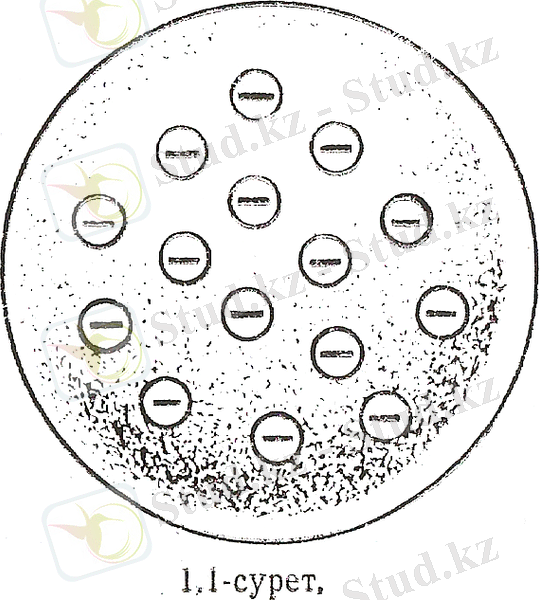 Атомның бірінші моделін 1902-1904 жж. Дж. Томсон ұснған. Бұл модель бойынша оң зарядталған біртекті атом массасына тербелмелі қозғалыста болатын теріс зарядты электрондар орналасқан, яғни атом бейнелеп көрсетсек «мейіз қосылған булка нан» сияқты (мейіз түйірлері электрон ролін атқарады), оң заряд атомның бүкіл көлемін түгелдей жайлайды деген (6-сурет) .
Атомның бірінші моделін 1902-1904 жж. Дж. Томсон ұснған. Бұл модель бойынша оң зарядталған біртекті атом массасына тербелмелі қозғалыста болатын теріс зарядты электрондар орналасқан, яғни атом бейнелеп көрсетсек «мейіз қосылған булка нан» сияқты (мейіз түйірлері электрон ролін атқарады), оң заряд атомның бүкіл көлемін түгелдей жайлайды деген (6-сурет) .
Бұл модель термоэлектрондық эмиссия кезінде электрондардың ытқып шығуын, атомның электромагниттік толқындарды шығаруын, иондардың пайда болу процестерін және т. с. с. құбылыстарды түсіндіре алады. Әрине, Томсон моделі атом туралы ілімнің дамуында белгілі роль атқарды.
Ағылшын ғалымы Резерфорд 1908-1911 ж. ж. жүогізілген тәжірибелерінде
6-cурет. атом ішіндегі зарядтың таралуын зерттей
отырып Томсон моделінің қате екенін дәлелдеді. Резерфорд тәжірибелерінде жұқа алтын фольга арқылы өткендегі α-бөлшектердің шашырауын қарастырды (алтынның созымдылық қасиеті өте жоғары, одан өте жұқа фольга жасауға болады) . Тәжірибеде қолданылған фольга қалыңдығы-6∙10 -7 м шамасында. Моноэнергетикалық, яғни энергиялары 7, 68 МэВ α-бөлшектердің көзі ретінде радиоактивтік препара-Ро-214 қолданылған.
1909 ж. Жүргізілген тәжірибелерінен Резерфорд α-бөлшектердің заряды оң, ал шамасы 2 е -ге тең, екенін тапқан еді. α-бөлшектердің шашырауын зерттейтін құралдың схемасы 7-суретте берілген.
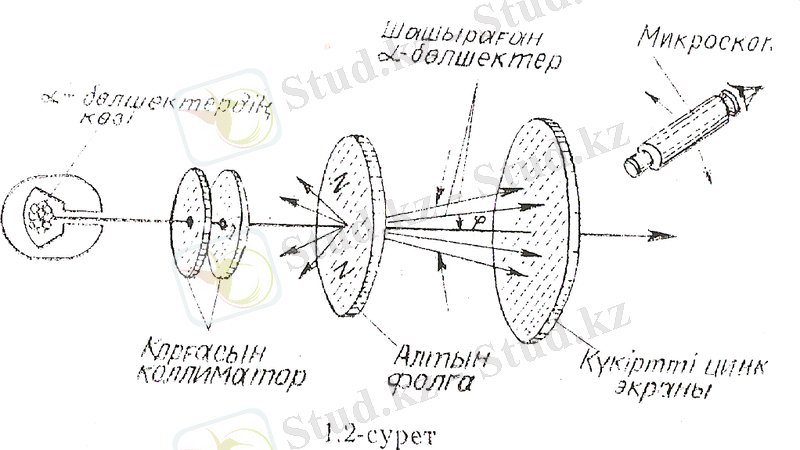
7-сурет.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz