Жартылай өткізгіштерде жарықтың жұтылуын зерттеу

Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 48 бет
Таңдаулыға:

Қазақстан Республикасы Білім және Ғылым Министрлігі
Қазақ Мемлекеттік Қыздар Педагогикалық Университеті
физика – математика факультеті
физика кафедрасы

Дипломдық жұмыс

Жартылай өткізгіштерде жарықтың жұтылуын зерттеу

050110 – физика мамандығы бойынша

Алматы - 2010
Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ... ..3

I–тарау. Жарықтың жұтылу механизмдері
1. 1 Меншікті жұтылу және зоналық
құрылым ... ... ... ... ... ... ... ... ... ... ... ... ... ... 4
1. 2 Меншікті жұтылу шегі: оның температураға, қысымға, қатты ерітіндінің
құрамына
тәуелділігі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ..9
1. 3 Экситондық
жұтылу ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... .21

II–тарау. Жарық жұтылуына электр және магнит өрістерінің әсерлері
2. 1 Магнит өрісіндегі зоналық
ауысулар ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..25
2. 2 Франц–Келдыш эффектісі (электрлік жұтылу және электрлік
шағылу) ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ...32
2. 3 Жартылай өткізгіштерге қоспа қосылған кезде
жұтылу ... ... ... ... ... ... ... . ... 37

III–тарау. Жарық жұтылуының әртүрлі жартылай өткізгіштердегі механизмдері
3. 1 Полярлы жартылай өткізгіштердегі торлық
шашырау ... ... ... ... ... ... ... ... ..47
3. 2 Көп фононды
жұтылу ... ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ...51
3. 3 Жарықтың меншікті жұтылу шегінің кванттық механикалық
түсіндірілуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... ... ..55

Қорытынды ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ..61
Пайдаланылған
әдебиеттер ... ... ... ... ... ... . ... ... ... ... ... ... ... ... ... ... ..
... ... ...62

Кіріспе

Жартылай өткізгіштер практикада және техникада кеңінен қолданылады.
Осыған байланысты олардың физикалық қасиеттерін зерттеу жартылай
өткізгіштер физикасында үлкен орын алады. Жарық түскенде жартылай
өткізгіштің физикалық қасиеті металға қарағанда, басқаша өзгереді; яғни
оның ток тасымалдаушыларының концентрациясы артады, электр өткізгіштігі де
арта бастайды. Сонымен қатар оның жұтылу коэффициентімен тыйым салынған
зоналарының энергиясының байланыстары әртүрлі болады. Міне осыған орай
жасалынған эксперименттік жұмыстың нәтижесін қарапайым электрондық теорияға
салыстырып, оның электрон–фонондық әсерлесу жолдарымен алынған теорияны
қарапайым жолмен түсіндіруге болатынын байқадық.
Сонымен қатар мектепте жартылай өткізгіштер тақырыбына аз сағат бөлінген.
Міне осы айтылғандарды ескере отырып менің дипломдық жұмысымның тақырыбын
Жартылай өткізгіштерде жарықтың жұтылуын зерттеу деп алдым.
Дипломдық жұмысымда осы тақырыптар бойынша шет тіліндегі әдебиеттердегі
теориялық және эксперименттік нәтижелерді тауып, оларды қазақшаға аудардым.

Табылған нәтижелерді мынадай мазмұндарға бөлдім.
I – тарауда жарықтың жұтылу механизмдерін, яғни оның ішінде меншікті
жұтылу оның зоналық құрылымын, жұтылудың шегін, оның температураға, қысым
және қатты ерітінділер құрамына тәуелділігін қарастырдым. Осыларға қоса
экситондық жұтылудың да механизмдерін көрсеттім.
II – тарауда жарық жұтылуына электр және магнит өрістерінің әсерлері
ретінде магнит өрісіндегі зоналық ауысулар, Франц – Келдыш эффектісі және
жартылай өткізгіштерге қоспа қосқан кездегі жұтылуды қарастырдым.
III – тарау бойынша жарық жұтылуының әртүрлі жартылай өткізгіштердегі
механизмдеріне полярлы жартылай өткізгіштердегі торлық шашырау, көп
фононды жұтылу және жарықтың меншікті жұтылу шегінің кванттық механикалық
түсіндірулерін жатқыздым.
Дипломдық жұмысымның негізгі мақсаты қарапайым теориялық жолмен
есептелген нәтижелерді эксперименттік нәтижелермен салыстыру. Сонымен бірге
алынған нәтижелердің физикалық мәндерін түсіндіру.
Менің бұл дипломдық жұмысым оқушылардың назарын жартылай өткізгіштер
туралы мәліметтер алу үшін өте қажетті деп ойлаймын.

I–ТАРАУ. ЖАРЫҚТЫҢ ЖҰТЫЛУ МЕХАНИЗМДЕРІ

1. 1 Меншікті жұтылу және зоналық құрылым

Бұл тарауда жарықтың меншікті жұтылуын және сонымен бірге зоналық
құрылымын, меншікті жұтылу шегінің температураға, қысымға және қатты
ерітіндінің құрамына тәуелділігін қарастырамыз.
Жартылай өткізгіште электромагниттік сәуле шығаруды тарату температура
мен қысымға тәуелді, сондай–ақ электр және магнит өрісіне де тәуелді
болады. Бұл эффекттерді өлшеу зоналық құрылым және жартылай өткізгіштердегі
энергия деңгейлері туралы мәлімет береді. Жұтылу коэффициентін өлшеу үшін
шағылу және өткізу коэффициенттері арасындағы, ал сонымен бірге
Крамерс – Крониг қатынасын пайдаланамыз. Есептеуді жеңілдету үшін
энергия кванты 1 эВ–қа тең, толқындық сан см-1 және толқын ұзындығы
мкм.
Жартылай өткізгіштерде тасымалдау құбылыстарын түсіндіру үшін валенттік
зона мен өткізгіштік зона арасында тыйым салынған зонаның бар екенін және
оның ені болатынын болжауды енгізу керек. Идеал жартылай
өткізгіштерде тыйым салынған зона ішінде энергетикалық деңгей жоқ
болғандықтан, мұндай жартылай өткізгіш жарық үшін мөлдір, ал оның бұрыштық
жиілігі кризистік мағынасынан аз болғандықтан төмендегі қатынаспен
анықталады

(1. 1. 1)
яғни, жарық кванттарын жұту электрондарды валенттік зонадан өткізгіштік
зонаға жеткізу шартына сай. Бұл жұтылу меншікті деп аталады; - шамасы
меншікті жұтылу шегін анықтайды.
Жоғарыда айтылған идеал емес жартылай өткізгіштердің жағдайында да дұрыс
болады, егер заряд тасымалдаушылар концентрациясы аса көп болмау керек,
яғни өткізгіштік металдікіндей болу үшін және ток тасымалдаушылармен жұтылу
меншікті жұтылу деңгейіне шамалас болады.

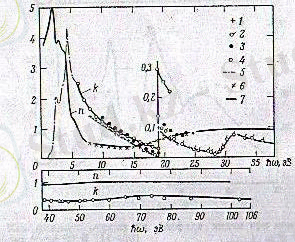
1–сурет. Германийдің жұтылу коэффициентінің және сыну көрсеткішінің
фотон энергиясына тәуелділігі
(1)–суретте германийдің жұтылу коэффициенті мен сыну көрсеткішінің
фотон энергиясына тәуелділігі көрсетілген [1–4]. Жұтылу көрсеткіші фотон
энергиясы (0,7 эВ) тыйым салынған зона енінен аз болса нөлге жақын болады,
содан ол максимум мәнге дейін артады, мұнда энергия бірнеше электронвольтқа
жетеді және тағы азаяды, егер энергия рентген сәулелерінің энергиясына
сәйкес болғанда максимумында және диэлектрлік өтімділік 32–ге
жуық.
Сыну көрсеткіші n спектр бөлігі үшін спектріне Крамерс–Крониг

қатынасы негізінде есептелді.
Бұл шама 8–ден 20 эВ энергиясы интервалында эксперименттік шамалармен
дәлелденеді, мұнда сыну көрсеткіші бірден аз. Аз энергиялар саласында
сыну көрсеткіші 4–ке жетеді, бұл диэлектрлік өтімділіктің нақты
мәніне келеді. Рентген аймағында сыну көрсеткіші бірге ұмтылады.
Осындай нәтижелер басқа да жартылай өткізгіштер үшін алынған.

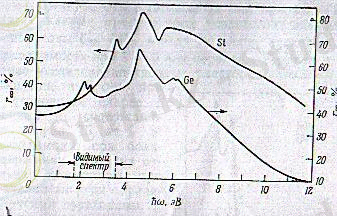
2 – сурет. Бөлме температурасында германий мен кремнийдің шағылу
коэффициентінің ға тәуелділігі

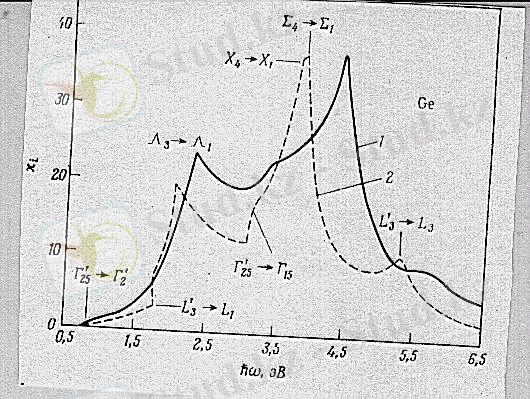
3 – сурет. Германийдің диэлектрлік өтімділігінің жорамал бөлігі 1- шағылу
коэффициентін өлшеу негізінде алынған; 2- Брусто және т.б. есептеген

(2)–суретте шағылу коэффициенті германий мен кремний үшін 12 эВ–қа
дейін энергия функциясы, ал (3)–суретте германий үшін диэлектрлік
өтімділіктің жалған бөлігі көрсетілген. Шағылу коэффициенті -
және шамасы энергияның бірдей мәндерінде максимумдары бар. Шағылудың
максимал коэффициенті 70 % - ға жетеді. шамасы зоналық құрылым
негізінде есептелген нәтиже (3)–суретте штрихталған сызықпен көрсетілген.
Осы екі қисық арасында сапалы ұқсастық бар; 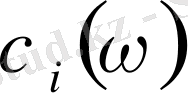тәуелділігінің
максимумдарын энергетикалық зоналар арасындағы ауысулармен байланыстыруға
болады.
эВ болғандағы ең үлкен максимум екі ауысуға негізделген:
біріншісі–валенттік зонадан 100 бағытта Бриллюэннің бірінші зонасының
шекарасындағы жақын өткізгіштік зонаға және екіншісі 110 бағытта .
Барлық белгіленген ауысулар, оның ішінде 6 эВ–тағы максимумдарға сәйкес
келетін ауысулар ауыр кемтіктер зонасынан нүктесінде іске асады,
мұнда жеңіл және ауыр кемтіктер туындаған, (0,8 эВ) және (3 эВ)
ауысулар қисығында қисаюға (майысуға) әкеледі. Бриллюэннің бірінші
зонасындағы нүктелермен осьтердің грекше және латынша бас әріптермен
белгіленуі топтар теориясымен және кристалл торының симметриялылығына
сәйкес зерттеулермен қатар енді [2].
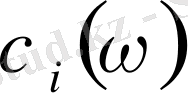тәуелділігінің графигінде теориялық максимумдар эксперименттік
мәндерге қатысты төмен энергиялы жағына қарай ығысқан. Осыған байланысты
қосымша параметрлерді енгізу арқылы сәйкестікті жақсарту қажеттілігі
туындауы мүмкін. Әйткенмен, көрсетілген есептеулерде есептеулер күрделі
болғандықтан, тек үш үйлестіруші параметрлер ғана қолданылғанын айта кету
керек.

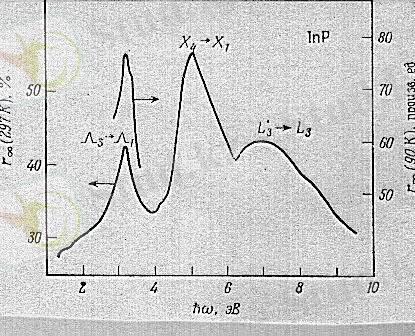
4 – сурет. 90 К және бөлме температурасындағы индий фосфидінің шағылу
коэффициенті

Германий мен кремнийдің шағылу спектрлері, зоналық құрылымның жалпы
сипатына өте ұқсас. Өткізгіштіктің ішкі зоналарының орналасуында
айырмашылықтар бар: кремнийде ішкі зонасы іс жүзінде –пен
сәйкес, сондықтан ішкі зонасы –ден жоғары емес төмен орналасқан.
Мұнда және энергиялар айырымы германийге қарағанда үлкен,
осының салдарынан өткізгіштік зонаның негізгі минимумы L1 – де емес
–де болады. Осының нәтижесінде кремнийде эВ–тағы шағылу
максимумы, эВ болғанда германийдегі ауысулармен салыстырғанда
басқа ауысулармен байланысты; бірақ қайсылары екендігі белгісіз: мүмкін
валенттік зонаның төбесімен болғандағы өткізгіштік зона арасындағы
немесе және ауысулар болуы мүмкін. Германий мен
кремнийдің қатты ерітінділерін оптикалық зерттеулер 3,4 эВ – та максимум Si
кремнийде 75 % маңында кремнийдің азаюымен бірге әлсірей түсетіндігін
көрсетті.

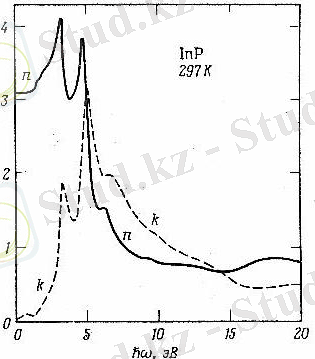
5 – сурет. Крониг – Пенни талдау әдісімен алынған, 4–суреттегі
деректер бойынша алынған индий фосфидінің сыну және жұтылу көрсеткіштері

Көріп отырғанымыздай, германий көп болғанда энергияның бұл мәніндегі
шағылдырушы қабілет басқа ауысулармен анықталады. Мысал ретінде InP индий
фосфиді жартылай өткізгіш қосылыстарды аламыз және оның шағылдыру
коэффициентін (4–сурет), сонымен бірге және көрсеткіштерін
қарастырамыз (5–сурет). Индий фосфиді мен германийдің зоналық құрылымдары
ұқсас. Төменгі температураларда максимумның 0,14 эВ шамаға ыдырауы
байқалады, бұл валенттік зонаның спин–орбиталдық ыдырауы салдары ретінде
қарастырылады. 0,28 эВ–тағы бұл максимумның ыдырауы германийде де байқалды.
Атомдық салмақ артқан сайын ыдырау энергиясы артады және AlSb алюминий
стибиаты үшін 0,75 эВ және GaSb галлий стибиаты, InSb индий стибиаты үшін
0,8 эВ-қа жетеді.

1. 2 Меншікті жұтылу шегі: оның температураға, қысымға, қатты ерітіндінің
құрамына тәуелділігі

(1.1.1)–формулаға сәйкес, тікелей тыйым салынған зонаның еніне байланысты
меншікті жұтылу шегін қарастырайық. (6) және (7) – суреттерде әртүрлі
температуралардағы галлий арсениді мен германийдегі жұтылу спектрлері
көрсетілген. Екі жағдайда да тыйым салынған зонаның ені температура
артуымен бірге төмендейді.

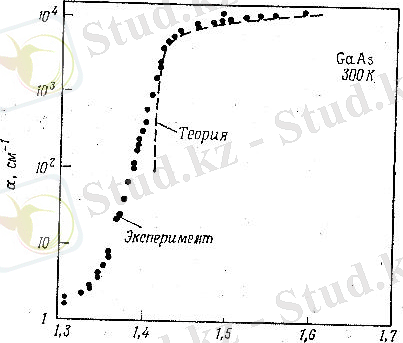
6–сурет. Бөлме температурасында галлий арсенидіндегі жарықтың жұтылу шегі

(8)–суретте германийдің тыйым салынған зона енінің температураға
тәуелділігі көрсетілген. Ол 150 К–нен жоғары температурада 0,43 мэВК
пропорционалдық коэффициентімен сызықты. Тыйым салынған зонаның ені бірге
айрықшаланатын жартылай өткізгіштерде бұл коэффициент екі мәртеден артық
өзгермейді: Мысалы, галлий фосфиді үшін (мұнда ) бұл коэффициент 0,54
мэВК, ал InSb индий стибиаты үшін (мұнда 300 К- де) ол 0,28мэВК– ге
тең. PbS қорғасын сульфиді, PbSe қорғасын селениді және PbTе қорғасын
теллуридінде тыйым салынған зонаның ені температура артуымен бірге
ұлғайғанымен кему қалыпты болып саналады.

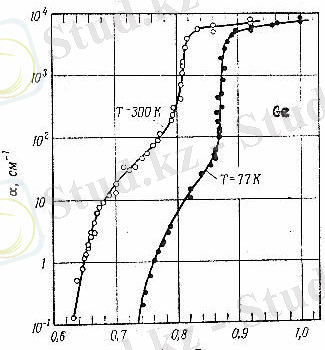
7–сурет. 77 К және 300 К температурада германийдегі жарықтың жұтылу шегі

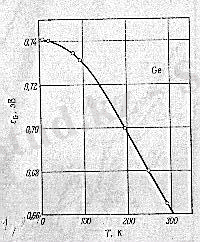
8 – сурет. Германийдің тыйым салынған зона енінің температураға тәуелділігі

(6) және (7)–суреттерді салыстырып галлий арсенидімен германийдің жұтылу
коэффициенттерінің энергияға тәуелділіктерінің аздаған айырмашылығын
байқауға болады. Германийде галлий арсенидінде болмайтын иілу байқалады.
Бұл иілу, германийде өткізгіштік зонаның негізгі минимумының Бриллюэннің
бірінші зонасының шегінде жататындығына негізделген, ал галлий арсенидінде
ол k=0 нүктесінде. Екі кристалдың валенттік зонаның максимумы k=0
нүктесінде орналасқандықтан, (1. 1. 1.) - өрнекке бағынатын ауысу
германийде импульстің өзгеруімен, ал галлий арсенидінде импульстің
өзгеруінсіз іске асады. Бұл жағдай сызбанұсқа түрінде (9)–суретте
көрсетілген. Германийде екі ауысу да іске асуы мүмкін, әйткенмен аз қажет
етілген энергияға қарамастан, тура емес ауысулар ықтималдығы аз, сондықтан
олар жұтылу қисығының иілуіне ғана әкеледі. Галлий арсенидінің өткізгіштік
зонасы (9) –суретте көрсетілген. Бұл жағдайда тура ауысулар аз энергияны
қажет етеді. Штрих–үзік тілше сызықтармен белгіленген тура емес ауысуларда
пайда болуы мүмкін, бірақ олардың ықтималдықтары аз және қажет етілетін
энергия үлкен болғандықтан жұтылу спектрінде байқай алмаймыз. Осы
ауысуларға байланысты галлий арсенидін тура жартылай өткізгіш, ал
германийді тура емес жартылай өткізгіш деп атайды [3].
Фотонның импульсі елеусіз аз болғандықтан, тура емес ауысулардағы
импульстің сақталу заңы басқа бөлшектің қатысуын қажет етеді. Ауысу кезінде
осы бөлшектің импульсі шамаға өзгереді. Мұндай бөлшек ауысу кезінде
жұтылатын жазық аралық фонон болуы мүмкін. Ауысу кезінде энергияның
сақталу заңы жұтылу жағдайында (1. 1. 1) – өрнектің емес,

(1. 2. 1)
(1. 2. 1) - өрнектің орындалуын қажет етеді, әйткенмен әдетте . Мұндай
бөлшек сонымен бірге қоспа атомы немесе дислокация болуы мүмкін. Бұл
жағдайда шашырау процесін жуық түрде серпімді деп санауға болады.
мәні Дебайдың кері ұзындығына қарағанда аз болуы керек. Әйткенмен, бізді
қызықтырған жағдайлардың көбісінде серпімді процестер фонондармен
әсерлесуге қарағанда сирек кездеседі.

9 – сурет. Германий және галлий арсенидіндегі тура және тура емес
ауысулардың сызба – нұсқасы

Жарықтың жұтылу коэффициенті негізінен матрицалық элементті дельта –
функцияға көбейтіндісімен және өткізгіштік зонадағы барлық мүмкін шекті күй
бойынша интегралданған ауысу ықтималдығына пропорционал. Бірінші жуықтауда
матрицалық элементті және - ке тәуелсіз деп санауға болады.
Сфералық зоналарды жуықтауда және (энергияның санақ басы
ретінде өткізгіштік зонаның төменгі жағы алынған), интегралдап мынаны
аламыз
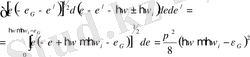(1. 2. 2)
Мұнда (кері жағдайда интеграл нөлге тең).
Фонон қатысқан кез келген ауысудағыдай мұнда матрицалық элемент
фонондардың таралу функциясына тәуелді. Осылайша жұтылу коэффициенті
осы функцияға пропорционал:
(1. 2. 3)
Мұндағы 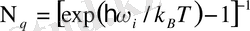тек тәуелділігінің салдарынан температураға әлсіз
тәуелді болатын тура ауысулармен салыстырғанда, тура емес ауысулар
шамасы температураға тәуелді болғандықтан, қосымша экспоненциалдық
тәуелділікке әкеледі.
Төменгі температураларда және жұтылу коэффициентінің мәні 10 см-1
шамасында болғанда, жұтылу спектрінде, бойлық және көлденең оптикалық,
сонымен қатар жазық аралық акустикалық фонондарға байланысты құрылым
байқалады.
Өткізгіштік зонаның негізгі минимумы 100 бағытында орналасқан, ал
зоналық құрылымы кремнийдікін еске түсіретін галлий фосфиді GaP жағдайы
үшін жұтылу спектрлері 10–суретте көрсетілген.

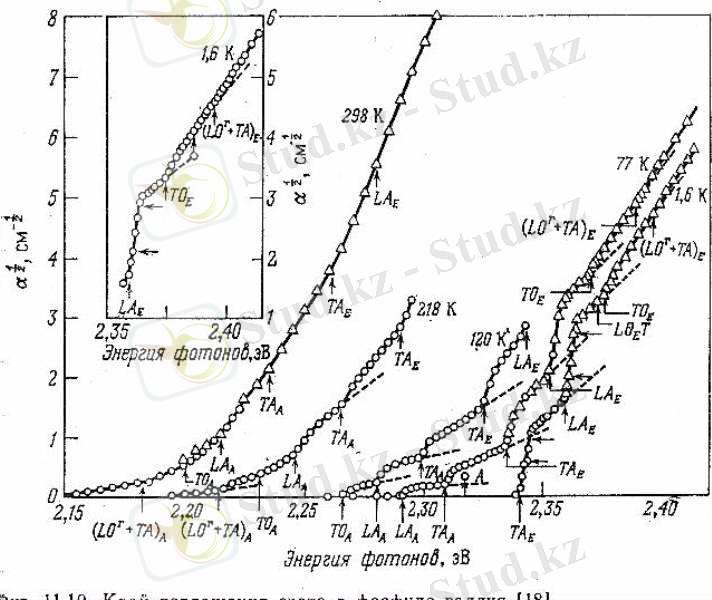
10 – сурет. Галлий фосфидіндегі жарықтың жұтылу шегі

Табалдырықтар экситондардың әсер етуі салдарынан айқын көрінеді. Осы
құрылымды ескермегенде, жұтылу коэффициентінің түбірі шын мәнінде төменгі
температурадағы фонондарды жұта отырып жүретін ауысуларды ескермеуге
болатындықтан сызықты түрде ға тәуелді.

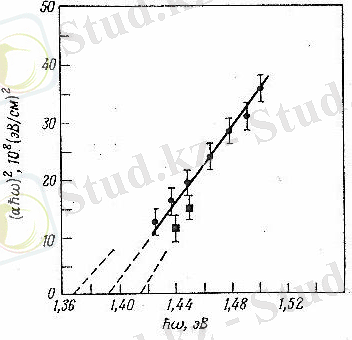
11 – сурет. Галлий арсенидіндегі жарықтың жұтылу шегі

Әдетте, меншікті жұтылудың шегін анықтау үшін қолданылатын әдіс
11–суретте келтірілген, мұнда шамасының фотон энергиясына (
жұтылу коэффициенті) тәуелділігі келтірілген. Эксперименттік нүктелер
түзу сызық бойында жатыр. Осы сызықтық абцисса осімен қиылысуы эВ
дәлдікпен 1,29 эВ тыйым салынған зонаның енін береді. Әйткенмен бұдан гөрі
жоғары дәлдікті магниттік оптикалық әдістермен алуға болады.
Кванттық теория негізінде көрсетілетіндей, жұтылу коэффициенті негізінен
жиілікке заңдылық бойынша тәуелді. -ты емес
көбейтіндісінің квадратын қолдану себебін оңай түсінуге болады. Электрон
күйден күйге сыну көрсеткіші -ге тең ортада
жылдамдықпен қозғалатын фотонды жұта отырып ауыссын делік. Бірлік уақыттағы
бірлік көлемдегі ауысулар санының барлық соңғы күй бойынша интегралын
ауысу жылдамдығы деп атаймыз. көлемдегі фотондар саны , ал
фотондар ағыны деп жобалап, шамасын фотондар ағынының
жұтылу коэффициентіне көбейтіндісі түрінде өрнектеуге болады, бұдан

(1. 2. 4)
энергия ағыны фотондар ағынының фотон энергиясына
көбейтіндісіне тең:

(1. 2. 5)
Басқа жағынан, шамасы Пойтинг векторының уақыт бойынша орташа
мәніне тең
.
(1. 2. 6)
Жазық толқынның векторлық потенциалы
(1. 2. 7)
мұндағы А0 – осы потенциалдың амплитудасы, а – А бағыттағы бірлік вектор.
Магниттік емес ортада Е электр өрісінің кернеулігі және Н магнит өрісінің
кернеулігі А векторлық потенциал арқылы өрнектеледі:

(1. 2. 8)

(1. 2. 9)
Мұнда скалярлық потенциал ескерілмейді, бұл төменде негізделеді.
поляризация векторы Е электр өрісінің кернеулік векторына параллель
бағытталған. уақыт бойынша орташа шаманы (1. 2. 6) – өрнектен
табамыз:

(1. 2. 10)
Толқындық вектордың модулі болатын көлденең электромагниттік
толқынның қарапайым жағдайында мынаны аламыз:

(1. 2. 11)
(1. 2. 4) және (1. 2. 5) – өрнектен N шамасын шығарып, жұтылу
коэффициентінің фотон энергиясына көбейтіндісін аламыз:

(1. 2. 12)
мұнда көбейтіндісінің орнына оның 377 Ом мәні жазылған.
(1. 2. 8) – өрнекте электромагниттік толқынның скалярлық потенциалын
ескермейміз. Электромагниттік сәулеленудің теориясынан оны әрқашан
калибрлеуші түрлендіру арқылы шығарып жіберуге болатындығы белгілі.
Импульсі электронның гамильтонианы бұл жағдайда қарапайым түрге
келеді:

(1. 2. 13)
Осы гамильтонианның көмегімен ауысудың R кванттық механикалық
ықтималдығы -ға пропорционал болатындығы көрсетіледі, бұл
көбейтіндісінің жұтылған жарықтың жиілігіне тәуелділігінің графигі
тұрғызылуының пайдалы екендігін көрсетеді [12].
Біз жұтылу шегінің температураға тәуелді болатындығын айтқанбыз. Жұтылу
шегінің ығысуы гидростатикалық қысымның әсерінен де пайда болады. (12) –
суретте галлий арсениді жағдайында осы құбылыс көрсетілген 9,4 мкэВатм
көлбеулікпен бастапқы көтерілгеннен кейін 8,7 мкэВатм көлбеулікпен түсу
басталады. Максимумы 60 000 атмосфералық қысымда. Мұндай жағдай, төменгі
қысымда өткізгіштік зонаның төменгі жағы k=0 нүктеде жатады деген
ұйғарыммен түсіндіріледі.

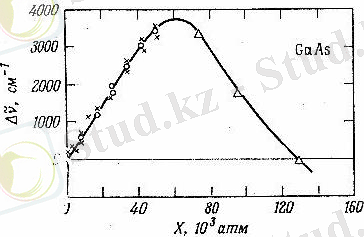
12 – сурет. Галлий арсенидіндегі жарықтың жұтылу шегінің Х гидростатикалық
қысымға тәуелділігі

Қысым артқан сайын, ол k=0 – де жатқан валенттік зонаның максимумына
қатысты көтеріледі. Әйткенмен 100 осінде және эквивалентті остерде
орналасқан қосымша жазықтықтар болады. Бұл жазықтықтар қысым артқан сайын
төмендейді. 60 000 атмосфералық қысымда қосымша жазықтықтар негізгі
жазықтықтан өте отырып, одан соң өткізгіштік зонаның төменгі жағын жасайды.

Германий үшін қысым коэффициенттерінің эксперименттік мәндері мынандай: 5
мкэВатм төменгі қысымда өткізгіштік зонаның төменгі жағын жасайтын 111
минимумы үшін, -2 мкэВатм 100 минимумы үшін және 12 мкэВатм 000
минимумы үшін. Осы уақытқа дейін зерттелген барлық жартылай өткізгіштер
үшін 100 минимумы үшін қысым коэффициенті теріс, ал Г және L–минимумдар
үшін ол әрқашан оң, соңғы жағдайда барлық жартылай өткізгіштер үшін мәні 4
мкэВатм – ға жақын.
Қатты ерітінділердің меншікті жұтылу шегінің құрамына тәуелділігі
компонентінің қысымға тәуелділігімен қандай да бір жолмен байланысты.
(13) – суретте тыйым салынған зонаның енінің германий – кремний қатты
ерітіндінің құрамына жарықтың жұтылуы бойынша анықталған тәуелділігі
көрсетілген.

13 – сурет. Германий – кремний қатты ерітіндісінің тыйым салынған зона
енінің құрамына тәуелділігі

Германийге бай ерітінділерде өткізгіштік зонаның төменгі жағы L – нүктеде
және кремний қоспада артқанда көтеріледі. Кремнийге бай ерітіндіде зонаның
төменгі жағы 100 минимумымен түзілген және баяу көтеріледі. Көріп
отырғанымыздай, L- және X - минимумдар кремний 15 атомдық % болғанда
қиылысады.
Осылайша n заряд тасымалдаушылардың жұтылу шегіне ықпалын қарастырамыз.
Мұндай ықпал электрондары аз эффективті массалы n – типті жартылай
өткізгіштерде байқалады. (14) – суретте индий антимониді үшін
бақылаулар нәтижесі көрсетілген.

14 – сурет. электрондар концентрациясы өскендегі индий антимонидінің
тыйым салынған зона тәріздес енінің Бурштейн ығысуы

n концентрация тен көп болғанда және электрондық газ туындаған кезде,
жұтылу шегі артқан сайын үлкен энергиялар жағына қарай ығысады.
Келесі өрнек

(1. 2. 14)
Осы ығысуды (Бурштейн ығысуы) Ферми энергиясымен байланыстырады.
(Тордың жылулық тепе – теңдіктегі электрондардың температурасы тор
температурасына тең) өткізгіштік зонада барлық энергетикалық деңгейлер
келесі энергияға дейін толтырылған деп есептейміз, яғни

(1. 2. 15)
( болғандықтан).

15 – сурет. Тура өткізгіштің энергетикалық зоналары моделіндегі Бурштейн
ығысуы (оң жақта Ферми – Дирактың таралу функциясының графигі көрсетілген)

Импульстің сақталу заңы фотонның минимал энергиясы тек энергия
қосындысынан ғана емес, (15) – суретте көрсетілгендей векторының сол
мәніндегі валенттік зонадағы күйдің энергиядан тұруын талап етеді:
(1. 2. 16)
электрон энергиясы (1. 2. 15) – өрнекке сәйкес анықталады.
Осылайша, жұтылу шегі үшін (1. 2. 14) – өрнек алынады. Параболалық
емес зоналар үшін бұл өрнек түрленуі керек.
Ферми энергиясы электрондар энергиясына, сонымен қатар олардың n
концентрациясына тәуелді. Шур, бұл тәуелділіктің туындаған жартылай
өткізгіштердегі электрондардың температурасы мен электр өрісі Е
кернеулігінің арасындағы қатынасты анықтауға мүмкіндік беретіндігін
көрсетті. Фонондар тура ауысуға қатыспайтындықтан, электронның
температурасына тәуелділіктен басқа температуралық тәуелділік орын алмайды.
Сондықтан тұрақты температурада және электр өрісінің кернеулігі
өзгергенде жүргізілген бір эксперименттің нәтижелерін, тордың температурасы
артатын ал Е=0 болатын келесі эксперименттің нәтижелерімен салыстыруға
болады. Екінші экспериментте , және осылайша электрон
температурасының Е электр өрісінің кернеулігіне тәуелділігі эмпирикалық
түрде алынады. Мұндай эксперименттер мысалы n – типті GaSb галлий стибиаты
үшін Т=77 К–де орындалды, таңбамен детектордың спектрлік
сезгіштігінің жарық интенсивтілігінің спектрлік таралуына көбейтіндісін, ал
мен туындаған үлгінің мөлдірлігін белгілейміз. Полихроматикалық жарық
детектор сигналының пайда болуын туғызады

(1. 2. 17)
мұнда .

16 – сурет. а) шамасының екі түрлі үлгі үшін электр өрісінің
кернеулігіне тәуелділігі
б) Сигналдардың қалыпты айырымдарының температуралық тәуелділігі, ол
детекторда жарықпен қоздырылған, А үлгісі ( типі, см-3)
және В үлгісі ( см-3) арқылы өткен және онда (1. 2. 14) –
қатынасының мәні есептелген. (штрихталған түзу) Бурштейн ығысуы
Егер электр өрісінің қабаттасуы электрондардың температурасының
артуына және шегінің ға ығысуына әкелсе, мөлдірлік ал сигнал
шарты орындалғанда,

(1. 2. 18)
шамаға өзгереді. Ең мүмкін ығысу туындаудың толық алынып тасталуына
сәйкес келеді және - ге тең. Осылайша сигнал қанығу деңгейіне
жетеді. (16, a) - cуретте шамасының электр өрісінің кернеулігіне
тәуелділігі көрсетілген. Концентрациясы үлгіде қанығу 150 Всм–де
пайда болады. Күштірек қоспаланған үлгілерде қанығу электр өрісінің
кернеулігінің үлкен мәндерінде туындайды.
Екінші экспериментте туындаған А үлгі үшін және туындамаған В үлгі үшін
() электр өрісі болмағанда түсірілген сигналдардың айырымының
температуралық тәуелділігі өлшенді. Бірінші эксперимент температурасы (77
K) бірлікке нормаланған бұл айырым (16, б) – суретте температура функциясы
түрінде келтірілген. (1. 2. 18) – өрнекке сәйкес сигналдың өзгерісі
Бурштейн ығысуының өзгерісіне пропорционал, ал соңғысы сонымен қатар -
ға пропорционал, (16) – суретте стрелкалар тізбегімен көрсетілгендей Е және
арасында қатынас табылуы мүмкін. Алынған қатынас (17) – суретте
нүктелермен көрсетілген.

17 – сурет. Бурштейн ығысуын есептеуден алынған n - типті GaSb галлий
стибиатындағы электр өрісінің кернеулігіне электрондар температурасының
тәуелділігі

Қисық энергия балансы теңдеуінен қозғалғыштықты және энергияның
релаксация уақытын ескере отырып есептелген. Есептік және эксперименттік
тәуелділіктер арасындағы сәйкестік қанағаттанарлық.

1.3 Экситондық жұтылу

Осыған дейін біз фотон жұтылғанда, бір–біріне тіптен тәуелсіз екі
квазибөлшектер деп электрон мен кемтікті қарастырдық. Шындығында бұл
әрқашан осылай емес. Атомдардың жұтылу спектрінен үздіксіз спектрге басқа
атомдардың қозуына негізделген жұтылудың дискретті сызықтары да болатындығы
белгілі. Жартылай өткізгіштерде мұндай қозулар кулондық әсерлесуге
байланысты электрон және кемтік түрінде көрсетілуі мүмкін. Сутегі атомының
моделіне сәйкес, байланыс энергиясын мына түрде көрсетуге болады
(1.
3. 1)
мұнда келтірілген эффективті масса;

(1. 3. 2)
статикалық диэлектрлік өтімділік. Бұл қозулар экситондар деп аталады.
Экситонның негізгі күйінің энергиясы шамасының 13,6 эВ Ридберг
энергиясына көбейтіндісіне тең; мысалы, және болғанда
мэВ аламыз. Осылайша, меншікті жұтылудың шегінен бірнеше
миллиэлектронвольтқа төмен жұтылудың дискретті сызықтары байқалады.
(18)–суретте мыс (I) оксиді үшін осындай спектр көрсетілген [8].

18 – сурет. T=4 K – дегі мыс (I) оксидіндегі экситондық жұтылу
спектрі

Осы экситондарда дипольдік ауысуларға тыйым салынғандықтан, спектр
сызықтары n=2 кванттық саннан басталады. Мысалы галлий арсениді үшін
бақыланған рұқсат етілген ауысулар, әдетте n=1 бір максимумын берсе,
жұтылудың қалған дискретті спектр сызықтары меншікті жұтылу шегімен
қабысады.

19 – сурет. 21 K – нен 294 K – ге дейінгі әртүрлі температуралардағы
галлий арсенидіндегі экситондық жұтылудың эксперименттік спектрлері

Меншікті жұтылу шегінен жоғары жұтылудың тұтас спектрі экситондарды
ескермей есептелген спектрден мына көбейткішке ерекшеленеді

(20)–суретте экситондардың ықпалын ескергендегі және ескермегендегі жұтылу
спектрлері көрсетілген. (19)–суреттен галлий арсенидінде Т=21 K
болғанда мэВ яғни бөлме температурасында экситондық максимал
толығымен өшіріледі, себебі фонондар байланыс энергиясындай энергияға ие
болады. Ток тасымалдаушылар концентрациясы үлкен жартылай
өткізгіштерде, сонымен бірге жартылай металдар мен металдарда экситондар
болмайды, себебі еркін ток тасымалдаушылар электрон – кемтік әсерлесуді
әлсіретеді. Бейтарап қоспалар максимумның кеңеюіне әкелсе, ал үлкен
концентрацияларда –экситондық сызықтардың жоғалуына әкеліп соғады.

20 – сурет. Қарапайым зоналық моделдегі тура ауысулар жағдайы үшін
есептелген жұтылу спектрлері

Тура жартылай өткізгіш болып табылатын галлий арсенидіндегі экситондарды
тура экситондар деп атайды. Тура емес жартылай өткізгіш болып табылатын
галлий фосфидіндегі (10)–суретте көрсетілген меншікті жұтылу шегі тура емес
экситондармен анықталады. Тура емес ауысулар фонондардың жұтылуы мен
шығарылуымен қоса жүреді. Экситондарға негізделген жұтылу, баспалдақ
түрінде іске асуы керек; баспалдақтар саны фонондар тармақтарының санынан
екі есе үлкен. Шындығында (10)–суретте көрсетілгендей жұтылу қисығында
иілулер байқалады. Осындай спектрлер сонымен қатар германий мен кремнийде
байқалады.
Өте төменгі температураларда тура емес жартылай өткізгіштерде (мысалы 1,6
K–де галлий фосфидінде) дискретті экситондық сызықтар байқалады. Бұл
сызықтар бейтарап донорлармен (байланысқан экситондар) экситондар деген
ұйғарыммен түсіндіріледі. Күкірт үшін галлий фосфидінде экситонның
байланыс энергиясы 14 мэВ, бұл осы донордың иондалу энергиясының 10 % - ын
құрайды.
Жоғарыда баяндалған сутегі атомының моделі негізінде экситонның Бор
радиусын есептеуге болады

(1. 3. 3)

Мұндағы - сутегі атомының Бор радиусы. Мысалы, және
үшін екендігін табамыз, бұл терең емес донорлар немесе
акцепторлардағы валенттік электронның орбитасының радиусына тең. Егер ток
тасымалдаушылар концентрациясы шамадан асса, мұндағы фермилік
толқындық вектор, онда заряд тасымалдаушылармен экситондардың экрандалуы
іске асады.
(1. 3. 3) – формуламен анықталатын салыстырмалы үлкен өлшемді экситондар
Ванье моделімен сипатталады. Френкель экситондарды инертті газ атомдарының
әлсіз әсерлесетін атомдарынан тұратын қатты денедегі экситондарды
қарастырды. Бұл жағдайда қозу жекелеген атомның немесе молекуланың қозуынан
ерекшеленбейді; [5] жақын көршілес – бөлшектердің әсерлесуін аз қозу
ретінде қарастыруға болады. Сондықтан Френкель экситонының радиусы бірнеше
ангстремнен аспайды, яғни тор тұрақтысының шамасына жақын. Мұндай
экситондар кейбір сілтілік галоидты қосылыстар мен органикалық фосфорларды
қолдана отырып талқыланған.
Егер экситон қозғалысына перпендикуляр магнит өрісі түсірілсе, онда
Лоренц күші теріс электронмен оң кемтікті ажыратуға тырысады. Экситонға бұл
әсерді диполь осі бойымен түсірілген электр өрісі жасайды; екі жағдайда да
жарық жұтылғанда Штарк эффектісі байқалады. Оны CdS кадмий сульфидінде
Томас және Хопфилд өлшеді. Бұл эксперимент түзілген экситонның
жылдамдығының нөлге тең емес екендігін көрсетеді. Экситондар жайлы неғұрлым
толық мағлұматты Декстер және Нокс кітаптарынан, Нокс мақаласынан алуға
болады.

II – тарау. Жарық жұтылуына электр және магнит өрістерінің әсерлері

2. 1 Магнит өрісіндегі зоналық ауысулар

Бұл тарауда жарықтың жұтылуына электр және магнит өрістерінің әсерлері
яғни магнит өрісіндегі зоналық ауысуларды, Франц–Келдыш эффектісін және
жартылай өткізгіштерге қоспа қосқан кездегі жұтылуды қарастырамыз.
Бұл параграфта магнит өрісінің өткізгіштік зона мен валенттік зонада
Ландау деңгейлерінің түзілуіне әкелетіндігі көрсетіледі. Бұл деңгейлердің
параболалық зонадағы энергиялары мына формуламен анықталады

(2. 1. 1)
мұндағы магнит өрісі осі бойымен бағытталған, m – эффективті масса,
циклотрондық жиілік:

(2. 1. 2)
n=0 болғанда, өткізгіштік зонаның төменгі жағы және валенттік зонаның
төбесі өзгергенде тыйым салынған зонаның ені артатындай болып
қозғалатындығын анықтаймыз:
(2. 1. 3)
мұндағы келтірілген эффективті масса (1. 3. 2 - өрнек). Меншікті
жұтылу шегінің сәйкес ығысуы эксперимент жүзінде алынған. Параболалық
зоналар үшін бұл ығысу магнит индукциясына пропорционал. Сызықтық
емес тәуелділік зоналардың параболалы болмауы салдарынан туындауы мүмкін.

21 – сурет. Бөлме температурасында магнит өрісіндегі InSb индий стибиатында
жарықтың жұтылу шегінің ығысуы
(21) – суретте магнит индукциясының әртүрлі мәнінде меншікті жұтылу шегі
маңындағы фотон энергияларына InSb индий стибиатының мөлдірлігінің
тәуелділігі көрсетілген. артқан сайын бұл шегі үлкен энергиялар жаққа
қарай ығысады. Бұл жағдайда ығысу ға пропорционал. (22)–суретте индий
арсенидінің өткізгіштік зона шегінің ығысуының магнит индукциясына
тәуелділігі көрсетілген.

22 – сурет. Индий арсенидінің тыйым салынған зона енінің магнит өрісіне
тәуелділігі

Әлсіз магнит өрістеріндегі сызықты емес тәуелділік Ландау деңгейлерінің
қарапайым моделімен түсіндіріледі. Күшті магнит өрістеріндегі сызықтық емес
тәуелділік көріп отырғанымыздай, өткізгіштік зонаның параболалы болмауына
негізделген.
Меншікті жұтылу шегінің ығысуынан басқа біршама үлкен энергиялар
облысында осцилляциялық тәуелділік байқалады. Бұл (23)–суретте k=0
болғанда германийде тура ауысулар жағдайы үшін көрсетілген.

23 – сурет. 0,044 және 3,6 Т магнит өрісі бөлме температурасындағы
германийдің осцилляциялаушы мөлдірлігі

(24)–суретте магнит индукциясына мөлдірлік минимумдарының орнының
тәуелділігі көрсетілген. Әрбір минимум үшін және арасындағы
тәуелділік сызықты. n=1 түзуінің көлбеулігі бойынша Г – жазықтағы
бөлме температурасында электрондардың эффективті массасы
анықталды. Осы әдістің дәлдігі басқа әдіске қарағанда жоғары.

24 – сурет. 23 – суреттегі минимумдар орнының магнит өрісіне тәуелділігі
Төменгі температурада, мүшесі (2. 1. 1)–өрнектегі бірінші мүшеден
аз болғанда валенттік зона мен өткізгіштік зонадағы Ландау деңгейлерінің
арасындағы ауысулар нәзік құрылымға ие. Күшті магнит өрістерінде Ландау
деңгейлері кванттық санмен анықталатын, электронның мүмкін болатын
екі спинінің салдарынан ажырайды. Зееман ыдырауының энергиясы

(2. 1. 4)
мұндағы g – электрон үшін Ланде көбейткіші, мкэВТ – Бор магнетоны.
(25)–суретте Т=4,2 K–де байқалған германийдегі тура ауысулардың нәзік
құрылымы мен сәйкес теориялық сызықты спектр көрсетілген. Валенттік зонада
ауыр, жеңіл кемтіктер ескерілді. Жұтылу жолақтарының барлығы екі ең
төменгілерін қоспағанда жуықтап сәйкес келеді, бұл жолақтар магнит
индукциясын нөлге дейін азайтқанда сақталады, сондықтан олар тура экситонды
ауысуларға жатқызылады [7].

25 – сурет. B=3,89 T магнит өрісінде 4,2 К температурада германийдегі
жұтылудың бақыланған және есептелген спектрлері

Германий үшін Ланде көбейткішінің мәні табылды. индий
антимониді үшін осылайша бұл көбейткіш өте үлкен теріс мәнге ие болатындығы
анықталды.
Жұтылу шегінің маңындағы шағылуға магнит өрісінің ықпалын (26)–суретте
көрсетеді. Өшетін гармоникалық осцилляторды мысалға ала отырып сыну және
жұтылу көрсеткіштерінің өзгерісін, осылайша шағылу коэффициентінің
өзгерісін есептеуге болады. Бұл модель сапалық түрде бақыланатын шағылу
спектрлерін түсіндіруге мүмкіндік береді.

26 – сурет. Фотондар энергиясы 236,7 мэВ және 85 К температурада InSb индий
стибиатындағы жазықтың зонааралық магниттік шағылуы

Магнит өрісінде тура ауысулардан басқа сонымен қатар тура емес ауысулар да
байқалды. Мысалы, (27)–суретте Ландау деңгейлерінің арасындағы, сонымен
қатар T=1,5 К–де германийде байқалған тура емес экситондық ауысулар
көрсетілген. ге экстраполяцияланғаннан кейін және шығарылатын фононның
энергиясын азайтқаннан кейін тыйым салынған зонаның ені эВ болды.

27 – сурет. Тура емес экситондық ауысулар (1) және Ландау деңгейлерінің
арасындағы (2) T=1,5 К – дегі ауысулар жағдайындағы магнит
индукциясына германийдің мөлдірлік минимумдар орындарының тәуелділігі
Экситондық ауысуларға байланысты мөлдірлік минимумының орны ке
магнит индукциясының үлкен мәндерінде ғана сызықты тәуелді болады. Әлсіз
магнит өрістерінде бұл тәуелділік параболалы (27)–суретте көрсетілген
германийдегі тура емес экситонның спектрлік сызығы екі сызыққа ажырауы
мүмкін: біреуі 2,1 мэВ байланыс энергиясына келесісі 3,2 мэВ байланыс
энергиясына сәйкес келеді. Көрсетілген қа тәуелділік және
бағыттары үшін әртүрлі; мұны әртүрлі кристаллографтық бағыттардағы фонондар
спектрінің әртүрлі болуымен; сонымен бірге шындығында Ланде көбейткіші
электрондар мен кемтіктер үшін – тензорлық шама екендігімен түсіндіруге
болады. Жоғары жиіліктер облысында спиндік резонанс бойынша эксперименттер
негізінде Ланде көбейткішінің шын мәнінде тензорлық сипатта болатындығы
анықталды [6].
Неғұрлым күшті магнит өрісінде Ланде көбейткіші Т болғанда тура
емес экситон сызығының ыдырауы байқалды. Ол Ландау деңгейлерінің спиндік
ыдырауы салдарынан пайда болады. Осы эксперименттер бойынша электрондар
үшін және Ланде көбейткіштерінің мәндері анықталды; олар
есептелген мәндерге сәйкес келеді. Мұндай өлшеулер үшін үлгінің қалыңдығы
бірнеше ғана микрометр болуы керек; оны жылулық кеңею коэффициенті басқа
тұғырға орнатуға болмайды, себебі суығанда деформация пайда болып
энергетикалық деңгейлердің туындауын жояды және магнит өрісінде спектрлік
сызықтар осылайша ыдырап кетеді. Жоғарыда сипатталған эксперименттерде
осындай алдын ала сақтық шаралары жасалды.

28 – сурет. Мөлдірлік минимумдарының орнының тура экситондық ауысулар (1
және 3) және 77 К температурада германийдегі Ландау деңгейлерінің
арасындағы ауысулар жағдайындағы магнит индукциясына тәуелділігі
(28)–суретте T=77 К–де германийдегі тура экситондарға негізделген
мөлдірлік орындарының өрістік тәуелділігі көрсетілген. 1 – қисықтың сызықты
бөлігінің болуы экситонның келтірілген эффективті массасын анықтауға
мүмкіндік береді. 3 – 5 түйісетін қисықтар тура тыйым салынған зонаның енін
мықтауға мүмкіндік береді: 77 K–де мэВ. Бөлме температурасында алынған
(24)–суреттегі нәтижелермен салыстыру Г–минимумда эффективті массаның
артып, ал тыйым салынған зонаның ені температура артқанда төмендейді деп
ұйғаруға мүмкіндік береді. Тура экситонның байланыс энергиясы .
Неғұрлым терең теориялық талдау 1,5 мэВ мәнге әкеледі. Ол сонымен қатар
күй үшін егер электрондар мен кемтіктердің эффективті массалары
бірдей болса магнит индукциясына сызықты тәуелді болмайды дегенді
көрсетеді. Бұл тек квадрат тәуелділік байқалатын мыс (I) оксиді болуы
мүмкін.

2. 2 Франц – Келдыш эффектісі
(электрлік жұтылу және электрлік шағылу)

Енді жартылай өткізгіштерде меншікті жұтылу шегінің маңындағы жарықтың
жұтылуына күшті электр өрісінің ықпалын қарастырамыз. Осы құбылыстың
теориясын Франц және Л. В. Келдыш берді. Бұл құбылыс энергетикалық тосқауыл
фотон туғызатын арқылы тыйым салынған зонаның еніне тең туннелдік ауысуы
деп аталуы мүмкін. Ол изоляторларда және жартылай өткізгіштерде де бар. Оны
ыстық электрондар эффектісінен ажырату үшін эксперименттік зерттеулер үшін
жартылай изоляциялайтын жартылай өткізгіштерді алған ыңғайлы.
Алдымен электрондар ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.