Сандық қатарлар: анықтамалар, қасиеттер және жинақталу критерийлері


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ
ҒЫЛЫМ ЖӘНЕ БІЛІМ МИНИСТІРЛІГІ
М. Әуезов атындағы Оңтүстік Қазақстан Мемлекеттік Университеті
«» кафедрасы
Тақырыбы: Сандық қатарлар
Орындаған: Шарипов Д.
Тобы: ИП-07-4к2
Қабылдаған: Такибаева Г.
Шымкент 2008ж
1. Сандық қатарлар
1. Сандық қатарлар.
Анықтама. Берілген ақырсыз u 1 , u 2 , u 3 , . . . u n , . . . сандық тізбектің мүшелерін плюс таңбасымен біріктіргенде шығатын символ
u
1
+ u
2
+ u
3
+ . . . + u
n
+ . . . =
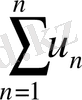 (I)
(I)
сандық қатар, ал u 1 , u 2 , u 3 , . . . u n , . . . сандары қатардың мүшелері, мәселен, u 1 -бірінші мүшесі, u 2 - екінші мүшесі, . . . , u n - п -ші, немесе жалпы мүшесі деп аталады.
Анықтама. (1) қатардың алдыңғы и мүшелерінің қосындысы
S
n
= u
1
+ u
2
+ u
3
+ . . . + u
n
=
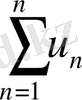 (n=1, 2, 3, …. ), (2)
(n=1, 2, 3, …. ), (2)
сол қатардың n- ші дербес қосындысы деп аталады.
Дербес қосындылар тізбегі S 1 , S 2 , S 3 , . . . , S n , . . . үшін мына үш жағдайдың бірі ғана орындалуы мүмкін:
1)
п
 -да дербес қосынды S
n
-нің шектеулі шегі S бap;
-да дербес қосынды S
n
-нің шектеулі шегі S бap;
2)
п
 -
да дербес қосынды
S
n
айқын таңбалы ақырсыз шек +
-
да дербес қосынды
S
n
айқын таңбалы ақырсыз шек +
 , не
, не
 - ке ұмтылады;
- ке ұмтылады;
3)
п
 -да дербес қосынды
S
n
ешқандай шекке ұмтылмайды (шегі жоқ) .
-да дербес қосынды
S
n
ешқандай шекке ұмтылмайды (шегі жоқ) .
Анықтама. Егер сандық қатар (1) -дің дербес қосындысы S
n
-нің
п
 -да шектеулі шегі
-да шектеулі шегі
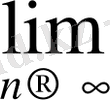 Equation. 3 S
n
=
S
бар болса, ол жинақты қатар, ал S саны сол қатардың қосындысы деп аталады.
Equation. 3 S
n
=
S
бар болса, ол жинақты қатар, ал S саны сол қатардың қосындысы деп аталады.
Егер
п
 -да, S
n
-нің шегі ақырсыздыққа ұмтылса немесе шегі мүлдем жоқ болса, (1) -ді жинақсыз қатар деп атаймыз.
-да, S
n
-нің шегі ақырсыздыққа ұмтылса немесе шегі мүлдем жоқ болса, (1) -ді жинақсыз қатар деп атаймыз.
Мысал ретінде геометриялық прогрессия мүшелерінен құралған, еселілігі
q
-ға тең
a+q+aq
2
+ . . . +aq"+ . . . =
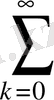 aq
k
(3) қатарын қарастыралық.
aq
k
(3) қатарын қарастыралық.
Әуелі
q
 Equation. 3 1
болатын жағдайдағы дербес қосындыны құралық:
Equation. 3 1
болатын жағдайдағы дербес қосындыны құралық:
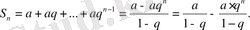
1) Егер
 < 1 болса, онда
< 1 болса, онда
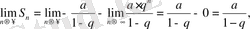 яғни (3) қатар жинақты, оның қосындысы
яғни (3) қатар жинақты, оның қосындысы
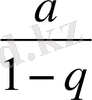 болады.
болады.
2) Erep
 >
1 болса, онда
>
1 болса, онда
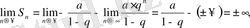 яғни (3) қатар жинақсыз.
яғни (3) қатар жинақсыз.
3) Erep
q =
1 болса, онда (3) қатар мынадай түрде жазылады:
а+а+а+ . . . -а+ . . . ,
онда
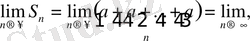 яғни (3) қатар жинақсыз.
яғни (3) қатар жинақсыз.
4) Erep q = -1 болса, онда
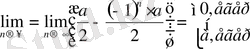 Equation. 3
Equation. 3
яғни
 ешқандай шекке ұмтылмайды, сондықтан да (3) қатар жинақсыз.
ешқандай шекке ұмтылмайды, сондықтан да (3) қатар жинақсыз.
Сонымен (3) қатар q < 1 болғанда жинақты да, ал q > 1 болса жинақсыз болады.
Анықтама. Берілген (1) қатардың алдыңғы
п
мүшесін шығарып тастағанда қалатын қатар
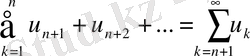 (4) берілген (1) қатардың
п
-ші қалдығы деп аталады.
(4) берілген (1) қатардың
п
-ші қалдығы деп аталады.
Егер жинақты қатардың қалдығының қосындысын R
n
арқылы белгілесек, онда S = S
n
+
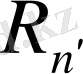 , R
n
= S - S
n
.
, R
n
= S - S
n
.
Теорема. Егер (1) қатар жинақты болса, онда
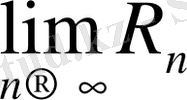 = 0.
= 0.
І-мысал. Қатар
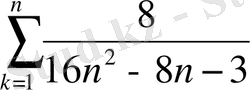 берілген. Оның алғашқы
п
мүшесінің қосындысы
S
n
-ді, анықтаманы пайдаланып, бұл қатардың жинақтылығын көрсету және оның қосындысы S - ті, қалдығының қосындысы R
n
табу керек.
берілген. Оның алғашқы
п
мүшесінің қосындысы
S
n
-ді, анықтаманы пайдаланып, бұл қатардың жинақтылығын көрсету және оның қосындысы S - ті, қалдығының қосындысы R
n
табу керек.
Шешуі. Рационал бөлшектің бөлімінің екі түбірі бар болғандықтан, оны екі сызықты көбейткіштің көбейтіндісі түріне келтіруге болады, яғни
16n 2 - 8n - 3 =0, n 1 = -1/4, n 2 =3/4;
16n
2
- 8n - 3 = 16
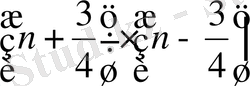 Equation. 3 = (4n + 1) (4n - 3) = (4n - 3) (4n +1) .
Equation. 3 = (4n + 1) (4n - 3) = (4n - 3) (4n +1) .
Қатардың жалпы мүшесін екі бөлшектің қосындысы түріне келтіреміз, яғни анықталмаған коэффициенттер әдісін пайдаланып, берілген бөлшекті қарапайым бөлшектерге жіктейміз:
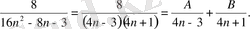
Тепе-теңдіктің екі жағын ортақ бөлімге келтіріп, алымдарын теңестіреміз:
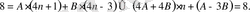
Сонан кейін, n-нің бірдей дәрежелерінің коэффициенттерін теңестіріп, мынадай теңдеулер жүйесін шешеміз:
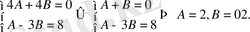
Сонымен,
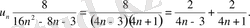
Енді берілген қатардың әрбір мүшесін екі қосылғыштың қосындысы етіп жазсақ, n -ші дербес қосынды мына түрде өрнектелер еді:
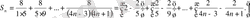
Сонда, берілген қатар үшін S, R n -ді оп-оңай табамыз:
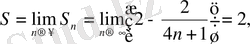
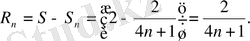
Көпшілік жағдайда, n - ші дербес қосындыны өрнектейтін жалпы формула табыла бермейді. Сондықтан, қатардың n-дербес қосындысының шегі бар, не жоқтығы жөніндегі мәселені жанама жолмен, яғни жинақтылық белгілерін пайдаланып шешуге тура келетінін ескерте кетелік.
2. Жинақты қатарлардың қарапайым қасиеттері. Теорема. Егер жинақты
 қатарының қосындысы S саны болып, ал с-берілген тұрақты сан болса, онда
қатарының қосындысы S саны болып, ал с-берілген тұрақты сан болса, онда
 қатары да жинақты болады жөне оның қосындысы
c·s
санына тең.
қатары да жинақты болады жөне оның қосындысы
c·s
санына тең.
Салдар. Егер
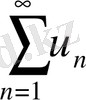 қатары жинақсыз болса, онда
қатары жинақсыз болса, онда
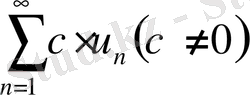 қатары да жинақсыз болады.
қатары да жинақсыз болады.
Теорема. Егер
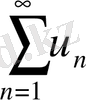 мен
мен
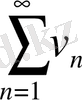 қатарлары жинақты болып,
S
пен
қатарлары жинақты болып,
S
пен
 сандары ол қатарлардың сәйкес қосындылары болса, онда берілген катарлардың сөйкес мүшелерін не мүщслеп қосу, не мүшелеп алу арқылы құрылған қатар
сандары ол қатарлардың сәйкес қосындылары болса, онда берілген катарлардың сөйкес мүшелерін не мүщслеп қосу, не мүшелеп алу арқылы құрылған қатар
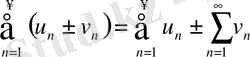 да жинақты болады және оның қосындысы
s ±
да жинақты болады және оның қосындысы
s ±
 санына тең.
санына тең.
Теорсма. Егер
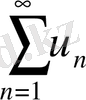 қатары беріліп
қатары беріліп
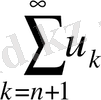 қатары оның кез келген қалдығы болса, онда осы екі қатар бірдей жинақты, немесе бірдей жинақсыз болады.
қатары оның кез келген қалдығы болса, онда осы екі қатар бірдей жинақты, немесе бірдей жинақсыз болады.
3. Қатардың жинақты болуының қажетті шарты.
Теорема. Егер
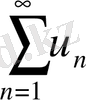 қатары жинақты болса, онда
қатары жинақты болса, онда
 -да оның жалпы мүшесі
и
п
нольге ұмтылады, яғни
-да оның жалпы мүшесі
и
п
нольге ұмтылады, яғни
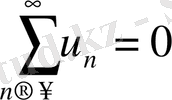 .
.
Салдар. (қатардың жинақсыз болуының жеткілікті шарты) . Егер
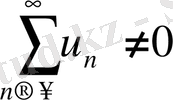 онда
онда
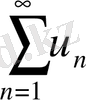 қатары жинақсыз болады.
қатары жинақсыз болады.
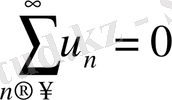 шарты болуы қажетті шарты, бірақ жеткілікті шарты еместігін ескерген жөн. Басқаша айтқанда, ол шарт орындалған жагдайда да қатар жинақсыз болуы мүмкін. Бұған мына гармониялық қатар
шарты болуы қажетті шарты, бірақ жеткілікті шарты еместігін ескерген жөн. Басқаша айтқанда, ол шарт орындалған жагдайда да қатар жинақсыз болуы мүмкін. Бұған мына гармониялық қатар
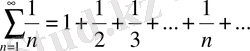 мысал болады. Мұнда
мысал болады. Мұнда
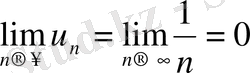 , бірақ қатар жинақсыз.
, бірақ қатар жинақсыз.
4. Қатардың жинақты болуының Коши критерийі.
Теорема. (Коши критерийі) .
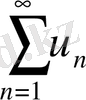 қатары жинақты болуы үшін берілген кез келген
қатары жинақты болуы үшін берілген кез келген
 >
0 саны үшін бір
N=N
(
>
0 саны үшін бір
N=N
(
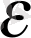 ) нөмірі табылып, сол қатардың мүшелерінің
n>N
теңсіздігін қанағаттандыратын нөмірлері үшін және кез келген натурал р саны үшін
) нөмірі табылып, сол қатардың мүшелерінің
n>N
теңсіздігін қанағаттандыратын нөмірлері үшін және кез келген натурал р саны үшін
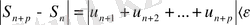 теңсіздігі орындалуы қажетті және жеткілікті.
теңсіздігі орындалуы қажетті және жеткілікті.
5. Мұшелері оң қатарлардың жинақтылығының жеткілікті белгілері.
Анықтама.
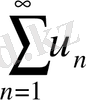 (1) қатарының мүшелері u
n
(1) қатарының мүшелері u
n
 Equation. 3
0 (n = 1, 2, . . . ) шартын қанағаттандырса, (1) қатар мүшелері оң қатар деп аталады.
Equation. 3
0 (n = 1, 2, . . . ) шартын қанағаттандырса, (1) қатар мүшелері оң қатар деп аталады.
Теорема. Мүшелері оң қатар
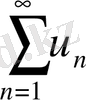 жинақты болуы үшін қатардың дербес қосындыларының тізбегі жоғарыдан шенелген болуы қажетті және жеткілікті.
жинақты болуы үшін қатардың дербес қосындыларының тізбегі жоғарыдан шенелген болуы қажетті және жеткілікті.
Енді, мүшелері оң қатарлардың жинақтылығынық кейбір жеткілікті шарттарын қарастыралық.
Салыстыру белгісі. Мүшелері оң
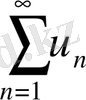 (1) мен
(1) мен
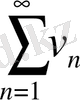 қатарларының мүшелері (белгілі бір n > N-нен бастап)
и
n
қатарларының мүшелері (белгілі бір n > N-нен бастап)
и
n
 V
n
шартын қанағаттандырса, онда:
V
n
шартын қанағаттандырса, онда:
1) (2) қатардың жинақтылыгынан (1) қатардың жинақтылығы шығады;
2) (1) қатардың жинақсыздығынан (2) қатардың жинақсыздығы шығады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz