Радикалдық сополимерлену

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Жоспар:

Радикалдық сополимерлену
Алфрей-Прайстың «Q - e»сызбанұсқасы

Радикалдық сополимерлену

Сополимерлену деп екі немесе одан да көп мономерлердің бірге полимерленуін айтады. Ол тәжірибе жүзінде өте көп қолданылады. Сополимерлену нәтижесінде әр түрлі қасиеттері бар полимерлер алуға болады. Мысал ретінде бутадиен мен стиролды соплимерлеу реакциясын келтірейік:

nCH ₂ =СН-CH=CH ₂ +mCH ₂ =CH=>[-CH ₂ -CH=CH-CH ₂ -] _n -[-CH ₂ -CH-] _m

C ₆ H ₅ C ₆ H ₅

Реакция нәтижесінде бутадиен-стирол каучугі алынады.

Радикалдық сополимерлену үшін жоғарыда қаралған барлық заңдылықтар тән. Бірақ бірнеше мономерлердің қатысуы реакция сатыларын қиындатады. Екі мономердің сополимерленуін қарайық. өсетін радикалдардың активтігі тек соңғы буынның табиғатымен анықталады деп ұйғарып, сополимерлену құрамының теңдеуін шығару үшін төрт қарапайым өсу реакцияларын ескереміз:

Өсу реакциялары Өсу реакцияларының

жылдамдықтары

М ₁ ^● +М ₁ =>М ₁ ^● V=k ₁₁ [М ₁ ^● ] [ М ₁ ]

М ₁ ^● +М ₂ =>М ₂ ^● V=k ₁₂ [М ₁ ^● ] [ М ₂ ]

М ₂ ^● + М ₂ =>М ₁ ^● V=k ₂₁ [М ₂ ^● ] [ М ₁ ]

М ₂ ^● +М ₂ =>М ₂ ^● V=k ₂₂ [М ₂ ^● ] [ М ₂ ]

мұнда М _i - і-типті мономер, М _і ^● -М _і буынымен аяқталатын макрорадикал, k _ji -М _і мономерінің М _j ^● радикалына қосылу реакциясының жылдамдық константасы.

Сополимерленген кезде мономерлердің реакцияға түсу жылдамдықтары мына теңдеулерімен сипатталады:

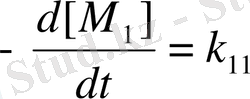[М ₁ ^● ] [ М ₁ ] + k ₂₁ [М ₂ ^● ] [ М ₁ ] (1)

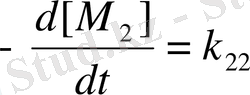[М ₂ ^● ] [ М ₂ ] + k ₁₂ [М ₁ ^● ] [ М ₂ ] (2)

Екі теңдеуді бір-біріне бөлсе осы реакция жылдамдықтарының қатынасы шығады:

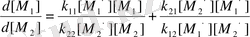(3)

Сополимерлену кезінде жүйеде квазистанциор күй туады, яғни әр түрлі активті орталықтардың концентрациясын тұрақтайды. Квазистанциор күйдің шарты:

k ₁₂ [М ₁ ^● ] [ М ₂ ] = k ₂₁ [М ₂ ^● ] [ М ₁ ] (4)

осыдан

[М ₁ 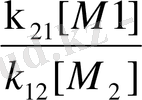^● ] = [ М ₂ ^● ] (5)

[М ₁ ^● ] мәнін (3) теңдеуіне қойып және де оның алымы мен бөлімін k ₁₂ k ₂₁ көбейтіп, кейбір жеңілдіктер жасағанда ол мынадай түрге келеді:

(6)

мұндағы r ₁ =k ₁₁ /k ₁₂ , r ₂ =k ₂₂ /k ₂₁ , r ₁ , r ₂ , шамалары мономерлердің салыстырмалы активтігі не сополимерлену константалары деп аталады.

Олар радикалға «өз» және «бөтен» мономерлердің қосылу реакция жылдамдықтарының қатынасын көрсетеді. r ₁ және r ₂ мәндері реакйияға түсетін мономерлердің табиғатына байланысты. (6) теңдеуі сополимерлер құрамның дифференциалдық теңдеу деп аталады. Бұл теңдеу r ₁ және r ₂ константаларын анықтау үшін мономерлердің сополимерге түрлену дәрежесі 5-7% аспайтын, полимерленудің бастапқы сатысында қолданылады. Мұндай жағдайда [M ₁ ] /[M ₂ ] қатынасы тұрақты, ал сол мезгілдегі лездік қатынас:

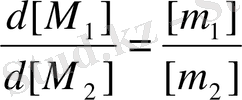
болса сополимер құрамының теңдеуі мына түрге ауысады.

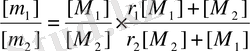(7)

мұндағы [m ₁ ] және [m ₂ ] мономерлер буындарының макромолекуладағы концентрациясы.

Сополимер құрамының мономерлер қатынасына тәуелділігін «мономер қоспасының құрамы-сополимер құрамы» диаграммасы арқылы бейнелеу ыңғайлы.

Бұл суретте сополимер құрамын сипаттайтын қисық сызықтардың негізгі түрлері көрсетілген. Қисық сызықтардың формалары r ₁ және r ₂ константаларының мәндеріне байланысты. Екі мономердің сополимерленуге бейімділігі осы r ₁ және r ₂ мәндерімен анықталады. Осыған орай мынадай жағдайлар мүмкін.

r1=r2=1мұнда екі мономердің де өсіп келе жатқан макрорадикалдарға қосылу активтігі бірдей, сондықтан сополимер құрамы мономерлер қоспасының құрамына тең және оның тізбегіндегі буындар статистикалық әдіспен орналасқан. Мұнда сопалимерлер идеалды дейді.

2) r ₁ >1, r ₂ >1 мономерлердің кез келген ара қатынастары үшін сополимер активтігі жоғары М ₁ мономермен байытылған.

3) r ₁ <1, r ₂ >1; мономерлердің кез келген ара қатынастары үшін сополимер активтігі жоғары М ₂ мономермен байытылған.

4) r ₁ <1, r ₂ <1; мұнда әрбір еркін радикал «бөтен» мономермен реакцияласуға бейім келеді де, сополимерде негізінен әр текті мономерлер кезктесіп тұрады. Құрам диаграммасында бастапқы мономерлер қоспасында М ₂ мен салыстырғандаМ ₁ өлшері кем болғанда, сополимер М ₁ буынымен байытылған, ал М ₁ мөлшері артық болғанда М ₂ буынымен байытылған.

5) r ₁ 0, r ₂ 0 сополимер құрамында мономер буындары бір-бірімен қатаң алмасып отырады. Бұл жағыдайда сополимерлердің құрамы бастапқы мономерлер қоспасының құрамына тәуелсіз, эквимолярлы.

6) r ₁ >1, r ₂ >1 бұл жағдайда сополимер алынбайды, әр мономер өзінше полимерленеді.

Сополимерлену константаларын (r ₁ және r ₂ ) тәжірибе жүзінде анықтауға болады. Олардың мәндері сополимер құрамын және тізбекте мономер буындарының орналасу ретін болжауға мүмкіндік береді.

Радикалдық полимерленуде r ₁ және r ₂ мәндері, демек сополимер құрамы, еріткіштің табиғатына және температураға онша тәуелді емес.

r ₁ және r ₂ мәндерін идеалды сополимерлену тұрғысынан қарастырса r ₁ r ₂ =1 шығады, яғни өсіп келе жатқан екі макрорадикалдың екі мономерді де қосып алу қабілеттілігі бірдей. Бұл шарт орындау үшін мына теңдік сақталу керек.

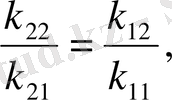
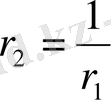
Идеал сополимерленетін біршама жүйелер бар. Мұндай жағдайда мономер буындары тізбекте кездейсоқ орналасады. Бірақ көп жүйелер үшін мономер мен радикалдағы полюстілік және кеңістіктік факторлардың әсерінен r ₁ r ₂ <1 болады да, мономер буындары [M ₁ ] және [M ₂ ] тізбекте алмасып тұруға ұмтылады.

Сополимерлену константаларын табу үшін көбінесе Майо-Льюис немесе Файнман-Росс әдістері қолданылады. Майо-Льюис әдісі бойынша сополимер құрамының теңдеуін (7) өзгертіп, мына өрнекті алады.

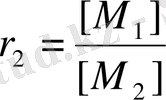
(8)

Бұл теңдеу бойынша r ₁ r ₂ -ге сызықты байланыста, ал [M ₁ ] /[M ₂ ] және [m ₁ ] /[m ₂ ] түзудің параметрлері. Осы қос параметрлердің мәндері түзу сызық береді. Мономерлердің әр түрлі ара қатынасында кемінде үш тәжірибе жүргізіп, әр қатынасқа сәйкес r ₂ =ƒ(r ₁ ) тәуелділігін беретін үш сызық алады. Түзулер бір нүктеде қиылысу керек, бірақ тәжірибе қателігінен олар белгілі бір аймақты береді.

Файнман-Росс әдісі бойынша [M ₁ ] /[M ₂ ] =F және [m ₁ ] /[m ₂ ] = ƒ деп белгілеп, сополимер құрамының теңдеуін өзгерту арқылы r ₁ және r ₂ мәндерінің арасындағы байланысты былай өрнектейді:

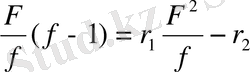
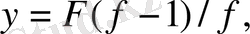
Тәжірибе нәтижелеріне байланысты тәуелділігіне сай график тұрғызады, мұндағы әр тәжірибе графикте бір нүкте береді, ал бірнеше тәжірибелерден түзу алынады. Түзудің түсу бұрышынан r ₁ , ал түзудің ординат осін қиятын кесіндіден - r ₂ табады.