Математика және музыка: үндестік пен қобыздың математикалық талдауы


ЖОСПАРЫ
- Кіріспе . . . 1б
- Негізгі бөлім . . . 3-18бб
- Қоңыр үнді, өте әуезді қазақтың көне музыкалық аспабының бірі қобыз жайлы . . . 3б
- Музыка үндестігі . . . 5б
- Музыканы математикалық жолмен талдау . . . 7б
- Музыка мен математиканың ортақ қасиеттері, байланысы . . . 9б
- Қорытынды . . . 19б
- Қосымшалар . . . 20-23бб
- А. Вивальди «Концерт соль мажор (I бөлім) . . . 20б
- Ықылас «Жез киік» . . . 21б
- Абай «Көзімнің қарасы» . . . 22б
- Тастанов «Алтай аясында» (I, II, III, IV бөлімдер) . . . 23б
- Қолданылған әдебиет тізімі . . . 24б
«Математика және музыка» тақырыбына жазылған ғылыми жобасына
ПІКІР
Математика мен музыканың тығыз байланысы өте ерте заманда байқалған. Бөлшек сандар пайда болған кезде
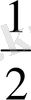 ;
;
 ;
;
 , . . бүтін сандарды нотаның ұзақтығына пайдаланған. Жоғарғы және төменгі дауыс жиілігін де физикада тербеліс теңдеуін косинус, синус графигін пайдалана отырып шешкен. Жұмыстың авторы математика, музыка, физика пәндерінің тығыз байланысын ғылыми жұмысын жазу барысында арнайы әдебиетпен таныса отырып, өзінің дүниетанымын, зерттеу нәтижелерін талдап, ұсынған.
, . . бүтін сандарды нотаның ұзақтығына пайдаланған. Жоғарғы және төменгі дауыс жиілігін де физикада тербеліс теңдеуін косинус, синус графигін пайдалана отырып шешкен. Жұмыстың авторы математика, музыка, физика пәндерінің тығыз байланысын ғылыми жұмысын жазу барысында арнайы әдебиетпен таныса отырып, өзінің дүниетанымын, зерттеу нәтижелерін талдап, ұсынған.
Бегалиева Ақерке ғылыми жұмысын орындау барысында музыка мен математиканың арасындағы үйлесімдікті пайдаланып, қазақ әндерінің ноталарын геометриялық фигураларға орналастыра білген.
Бұл ғылыми жұмыс музыка мектептерінде оқитын оқушыларға математикадан алған білімдерін тереңдетіп, музыкамен байланыстыруға болатынын ұсынып отыр.
Жұмыстың барысында математиканың музыкаға ықпалын әлі де зерттеу керек.
Ш. Уәлиханов атындағы №12 көп салалы гимназиясының 9 «А» сынып оқушысы
Бегалиева Ақеркенің «Математика және музыка» тақырыбына жазылған ғылыми жобасына
АННОТАЦИЯ
Бұл жұмыста музыка мен математиканың тығыз байланысы қарастырылған.
Аннотация
на научный проект Бегалиевой Акерке
на тему «Математика и музыка»
В этой работе рассмотрена тесная связь математики и музыки.
THE SUMMARY
on Begaliyeva Akerke’s scientific work
on a theme “Mathematics and music”
In this job the close connection of music and mathematics is considered.
КІРІСПЕ
Музыка-математикалық сана-сезім, ал математика-музыканың ақыл-ойы.
ағылшын математигі Д. Сильвестр
Математика мен музыка - ең ежелгі ғылымдар. Музыканың құрылысы математика заңдарына бағынатыны мыңдаған ғасырлар бұрын белгілі болған.
. . . Музыка математикалы, ал математика музыкалы. Екеуінде де сан идеясы мен қатынас билік етеді.
Ғалымдар шоғырының көшбасшысы Әбу Насыр әл Фараби, Ибн Сина, әл Хорезми, Әбдірахман Жәми, Дәруіш, Әли, әл Түркістани, тағы да басқа ойшылдар, ғылымның барлық саласында бірдей еңбек еткен ғұлама ғалымдар. Фарабидің ғылым және өнердегі үлкен де кесек дүниесі - оның музыкасы, ол ең әуелі музыканың аса ұлы теоретигі саналады. Оның музыка іліміне, теориялық негіздеріне арналған бірнеше еңбектері болған. Солардың бастылары - «Музыканың ұлы кітабы», «Музыка ғылымы турылы пікірлер», «Ғылымдар классификациясы», «Ырғақтар классификациясы туралы кітап». 1
Әл Фараби музыка теориясын мынандай бес салаға бөледі:
- Музыка туралы ілімнің негізі, зерттеу объектісі, тәсілдері.
- Музыка туралы ілімнің негіздері, тондары өзара байланысы мен қатынасы.
- Музыка теориясының негіздерін зерттеу тәсілдерін қолдана білу
- Тондардың негізін құрайтын музыкалық ырғақтар табиғаты.
- Музыкалық әуен, оны шығару жолдары (композиция) . 2
Зерттеулердің нәтижесінде музыканы тыңдайтын және немесе музыкамен айналысатын 25 000 американдық оқушылар математика тесттілерінен, музыкамен айналыспайтын балаларға қарағанда, жоғары балдар жинаған.
Ми бөлімдерінің жауапкершілік аймақтарын ауқымды зерттеуін Эрве Платель (Platel Herve) бастаған 8 адамнан тұратын халықаралық топ қолға алып, мидың кейбір бөліктері музыканың кейбір функцияларына жауап беретінін атап өтті. Зерттеуде музыкант емес алты жас француз, музыканы тыңдаған кезде мидың логикалық операцияларына жауап беретін бөлімдері жұмыс атқарғанын байқады.
Барлық орта ғасыр музыканттары сандық заңдылықтарды пайдаланған, мысалы атақты «Фибоначчи сандары». Пушкиннің «Моцарт және Сальери» трагедиясында Сальеридің Моцарттан айырмашылығы алгебраның үйлесімділігін тексерген және оның ежелгі дәстүр мен ғылымның сақтаушысы екендігі анықталған.
XX ғасырдың композиторлары қайтадан математикаға бет бұрды. Ставринский, Скрябин қайтадан «Фибоначчи сандарымен» эксперимент жасады және көркемдік түрі арқылы «алтын қимаға» сай пропорциялар құрды.
Музыка тәсілінің математика тәсілінен айырмашылығы көп емес екенін композиторлар жиі мойындайды. Бұл туралы көрнекті дирижер, профессионал математик Эрнест Ансерме былай дейді: «Музыка мен математиканың арасында сөзсіз паралеллизм бар екені анық. Бұл екеуі де ойдың іс әрекеті, олар бізді өмірдің күнделікті қателерінен сақтайды». Ол музыка мен математиканың абстрактілі екенін, тура және шынайы ұқсастықтары жоқ екенін атап өткен.
1712 жылы Гольбахқа жазған хатында Лейбниц музыкаға мынадай танымал анықтама береді: «өзін - өзі есептей отырып, музыка жанның арифметикалық жаттығуы екенін білмейді» деген.
Көптеген көрнекті музыканттар математиканы жақсы білген:
60 жылдары композитор Эдисон Денисов музыкаға тікелей математикадан келген, ол Томск университетінде математиканы оқытқан.
Көрнекті виолончелист К. Давыдов физика-математикалық факультетті бітірген, замандастарының есіне түсіруі бойынша «оның таза және қолданбалы математикаға керемет дарыны болған және оның үйінде өзі жасаған теміржол көпірінің макеті көпке дейін сақталған».
Леонид Сабанеев - Москва университетінің математика факультетін бітірген, керемет пианист, композитор.
Леонардо да Винчи тек қана суретші ғана емес, музыкант және математик, сонымен қатар архитектор, мүсінші, инженер, анатом, физик болған. Ол өзінің ғылыми негіздеріне көп көңіл бөлген. Бұл жөнінде ол ертедегі ұстазы әл Фарабиге көп ұқсайды. 3
Белгілі композитор София Губайдулина Россия және шетел премияларының лауреаты, Берлин өнер Академиясының құрметті мүшесі, оны Э. Денисов пен А. Шниткеден кейінгі, алдыңғы қатарлы 1960-1980 жылдардағы советтік «үштікке жатқызады». 4
Атақты грек оқымыстысы Пифагордан бастап, математиктер ылғи музыкаға қызығушылық танытқан. Математикалық музыка теориясы өзінің бастамасын Пифагор мектебінде алған. 5
НЕГІЗГІ БӨЛІМ
Математика ғылымдардың ішіндегі ең абстрактілісі, ал музыка өнердегі ең елеңдетуші (өнер мен ғылымның ең жоғарғы білдірушілері) болғандықтан, мен математика және өнер арасындағы қарым- қатынастар туралы ғылыми жобаны музыкадан бастаймын.
Домбыра, қобыз аспабы өте ерте кезеңде туып, дамып, жетілген. Қобыз аспабын бақсы сарынында жыр, терме, толғау үлгісіндегі эпикалық мақамда тартқан.
Тарихи айғақ: 694 жылы түркі тайпалары Түрік қағанатын қайта орнатқанда, қытайлықтар түркі тайпаларын бітімге шақырады. Сол тойда түркі тайпалары қобыз аспабының сарынымен жыр айтады. Мұны естіген қытайлықтар қобызды көктің үніне теңеген екен. 6
Бүгінде толық зерттеліп болмаған қобыз орта ғасырда бүкіл Орта Азияға мәлім болған. Қазақ даласында қобыз музыкасының атасы - Қорқыт, оның сарындары барлық бақсылар мен қобызшыларға үлгі болған. Ертеде бақсылар мен жыраулар қобызды сарнатқанда дауыл тұрып, алты қанат үй шайқалыпты дейтін аңыз - әңгімелер ел арасында көп. Ертеде поэзия мен қобыз культы діннен күшті болған. Мысалы, «Қорқыт ата кітабында» батырлар жауға аттанар кезде қобыз (нарқобыз) сарыны ойналады екен. Әрбір оғыз батыры беліне нарқобыз байлап жүретін болған. Жау қолына түскен Бәмсі - Байрақ (Алпамыс) өзін іздеп келген оғыз батырларына қобыз сарынымен хабар білдірген.
Қобыз аспабы туралы деректер Дәруіш Әли трактатында да кездеседі, ол: «Қобыз - жақсы үнді, өте әуезді, ішекті музыкалық аспап», - деген. Дәруіш Әли қобыздың алғашқы шығарушысы ретінде жалайыр Сұлтан Уәисті атайды. Қобыз ребабтың ұзартылған түрі.
Әбдірахман Жәми өзінің ХІV ғасырда жазған «Музыка хақындағы трактатында» ежелгі ғалымдардың музыка теориясына қатысты еңбектерін жинақтай келіп, Шығыс (Орта Азия) халықтарына тән ырғақ, әуен, мақымдарды классификациялайды. Үндестік заңдылықтары, екі музыкалық дыбыстың ара қатынасы (интервал) туралы теориялық ойларды дамыта түседі. 7
Әл Фараби «Музыкалық аспаптар» трактатында қобыз, уд аспабының құрылысы, ашық пернелері, оған орындаушы саусақтарының орналасуы, төрт ішекті қобыз, соның бойында жасалатын интервалдардың арақатынасы, дыбыс қатары, жағымды тондар, қобыз аспабын күйге келтірудің қарапайым және күрделі түрлері, оларды қолданудың тәсілдерін қарастырған. Әл Фараби уд, қобыз ішектерін пернелерге бөлу арқылы түрлі интервалдар (кварта, квинта, октава) жасаудың тәсілдерін, теориялық негіздерін көрсетеді. Мәселен, октава -
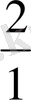 , квинта -
, квинта -
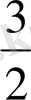 және кварта -
және кварта -
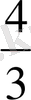 деп белгілеген.
деп белгілеген.
Қазақтың XIX ғасырдағы көрнекті қобызшылары Жанақ, Шөжелер де Қозы-Көрпеш жырын қобызбен орындаған.
Қобыздың музыкалық сарыны қазақ пен түркмен халықтарының арасында тәп-тәуір сақталған. Оның үлгілерін А. Затаевич пен В. Успенский жинаған, қобыз аспабы туралы тарихи деректер орыс ориенталистерінің еңбектерінде де кездесіп отырады. Мысалы, саяхатшы И. Гмелин алғашқылардың бірі болып бақсы қобызының түр-түсі мен құрылысын, орындау ерекшеліктерін зерттеген болса8, П. Паллас та қобызды суреттеп, бақсылардың сан түрлі сақиналармен жабдықталған даңғараға ұқсас аспапты қобыз деп атайтынын жазған. Белгілі орыс ғалымы А. Левшин де қазақ халқының негізгі музыкалық аспаптары ретінде қобыз бен сыбызғыны атайды. 9
Кеңес дәуірінде қобыз аспабының тегі мен құрылысын Қ. Жұбанов, Б. Сарыбаевтар зерттеген.
Әл Фараби ноталардың тербелмелі денелердің қозғалысынан шығатынын айтып, оның көрнекті дәлелі ретінде ішекті келтіреді. Ішектен дыбыс шығарғанда оны неғұрлым тартып қойса, дыбыстың қатты; босатса, әлсіз де төмен естілетінін айтады. . «Нота дегеніміз - өзі пайда болған дененің ішінде белгілі уақыт созылып тұратын жалғыз дыбыс», - дейді Фараби. 10 Оны бүгінгі ғылым да теріске шығармайды.
Музыка мінездемесінің ең маңыздысы оның дыбысының биіктігінде, тербелістің жиілігі тартылған ішектің сипаттамасына байланысты. Неғұрлым тербелістің жиілігі үлкен болса, соғұрлым дыбыс «биік» (қатты) болады.
Б. Тейлор ішектің ұзындығына, массасына және оның керілуіне байланысты оның тербеліс санын есептеп шығарған. Л. Эйлор, Д. Бернули, Ж. Даламбер ішектің тербелісінің толық теориясын жасап шығарып, ішектің негізгі үнін немесе тербелетін денені, яғни обертонды сүйемелдейтін қосалқы дыбыстардың пайда болуын түсіндіреді.
Ішектің тура, нақты математикалық теориясын жасағаннан кейін, музыканың тағдыры математикадан бөлінбейді. Математикалық анализға дыбыс, тембр, үйлесімділік, мәнерлілік жатады. Математиканың араласуы арқылы музыканың ең шығармашылық құрылысы басталады. 11
Музыкалық дыбыстар немесе тондар дыбыстың жоғарылығымен, қаттылығымен және тембрімен сипатталады. Тонның жоғарылығы дыбыстың қаншалықты жіңішке немесе жуан екендігін білдіреді.
Қобыздың ең жоғары тондарын алу үшін ішектің төменгі жағында, ал ең төменгі тонды алу үшін ішектің жоғарғы жағында ойнау керек.
Қобыз немесе үрмелі аспаптардан шығатын толқындардың формасы күрделі болады, бұларға күрделі музыкалық дыбыстар сәйкес келеді де, тербелістер жиілігінің қатынастары 1:2:3:4 қатынастарындай
тондардан тұрады. Негізгі тоннан басқа жиіліктері екі, үш, төрт есе көп
болатын басқа тондар обертондар деп аталады.
а)
б)
в)
г)
3-сурет
3-суретте қобыз туғызатын күрделі дыбыстың графигі көрсетілген.
а) қобыздың күрделі дыбысының графигі
б) қобыз дыбысының негізгі тоны
в, г) қобыз дыбысының ең интенсивті екі обертондарының графиктері
«Математика тек қана ақиқаттың ғана емес, сонымен қатар сұлулықтың иесі. Қатал, жоғары, таза және мінсіздікке ұмтылған ұлы өнер туындыларына ғана тән - сұлулық, » - дейді Б. Рассел.
ХVІІ ғасыр бойы теорияда музыка сандар туралы ғылым, яғни математиканың бөлімі деген пікір болған. Бұндай көзқарасқа Кеплердің «Әлем үйлесімі» еңбегі абыройлы, беделді ықпал етті. Кейінірек ХVІІІ ғасыр басында Лейбниц өзінің музыка туралы көптеген қолжазбаларында музыкалық үндестіктің табиғаты сандық өлшем негізінде құрылады, деп тұжырымдайды.
Әл Фарабидің музыка үндестігі туралы ойларында: ноталарды екіге бөлген, ол алғашқысын бастапқы, соңғысын қосалқы бөлігі деп атайды. Ол дыбыс үндестігі туралы сөз қозғағанда: «Егер зерттеуімізді жалғастыра түссек, онда ноталардың өзара байланысы, белгілі бір тәсілмен ауысып отырғанын көреміз. «Байланыс» деп екі немесе бірнеше ноталардың қосылуын, «қосарласу» деп ноталардың байланысын айтамыз. Ноталар арасындағы кейбір үндестіктер кемел де табиғи болып келсе, енді біреулері ондай болмайды. Ноталар арасындағы алмасу жайында да осыны айтуға болады», - деп жазған. 12
Әл-Фараби арифметикалық мәліметтерді пайдаланып әр түрлі музыкалық интервалдарды шығарып алу ережелерін береді. 13
Әл-Фараби октава интервалдарын алу жағдайын былай түсіндіреді:
«АВ аспап шегін алып, оны L нүктесінде тең екіге бөлеміз. АВ шегі
беретін дыбысты АL шегі беретін дыбысымен салыстырсақ, онда бірінші дыбыс екі еселенген екінші дыбысқа тең болады. Дыбыстың мәні оны тудыратын шектің ұзындығына тура пропорционал болады. АВ және LВ шектерінің ұзындықтарында пайда болатын интервал толық интервал, немесе октава деп аталады. «Екі еселенген толық интервал» екі еселік октава деп аталады. Бұл интервал толық интервалмен (октавамен) бірге «үлкен үндес интервалдардың» категориясына қосылады.
Әл-Фараби кварта интервалын төмендегіше алады:
АL кесіндісін Н нүктесінде тең екіге бөлеміз. АВ ішегінде алынатын АН дыбысы НВ және оның 1/3 бөлігінде пайда болатын Н дыбысына тең. А және Н дыбыстарын ажырататын интервал кварта деп аталады. А және Н дыбыстары бір біріне қарағанда 4:3 қатынасындай. Сондықтан ең жоғарғы дыбысты ең төмен дыбыспен салыстырғанда 1-дің 1+
 қатынасындай болады. Екі дыбыстың арасындағы интервал «орташа үндес интервалдарға» жатады. Екі еселік кварта үндес болмайды. Әл-Фараби осындай экспериментті теориялық зерттеу негізінде үндес және үндес емес музыкалық интервалдарды алудың ережесін ұсынады: «Интервалдардың ішіндегі «үндес интервал» деп қатынасы бүтін санның екі еселік қатынасын немесе бүтін қосу бүтін санның бөлігіне тең интервалдарды айтамыз, ал қалған интервалдар көп жағдайда үндес болмайды»14
қатынасындай болады. Екі дыбыстың арасындағы интервал «орташа үндес интервалдарға» жатады. Екі еселік кварта үндес болмайды. Әл-Фараби осындай экспериментті теориялық зерттеу негізінде үндес және үндес емес музыкалық интервалдарды алудың ережесін ұсынады: «Интервалдардың ішіндегі «үндес интервал» деп қатынасы бүтін санның екі еселік қатынасын немесе бүтін қосу бүтін санның бөлігіне тең интервалдарды айтамыз, ал қалған интервалдар көп жағдайда үндес болмайды»14
Егер квинтаны квартаға қоссақ, онда октаваны аламыз. Мысалы:

Әл-Фарби осы әдіспен октава мен квартаның, октава мен квинтаның және басқа интервалдардың қосындыларын анықтайды, яғни
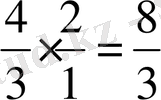 (октава қосу кварта) ;
(октава қосу кварта) ;
 (октава қосу квинта) .
(октава қосу квинта) .
Мұндай амалдардың нәтижесі берілген интервалдың ең жоғарғы сатысына жақын дыбыс санын береді. 15
Қосу ережесі немесе екі еселеу ережесі бізге екі еселік, үш еселік және төрт еселік кварта мен квинтаны, октава қосу квартаны, октава қосу квинтаны және т. б. Мәселен:
Екі еселік кварта
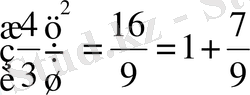 ;
;
Төрт еселік кварта
 ;
;
Октава қосу кварта
 ;
;
Октава қосу квинта
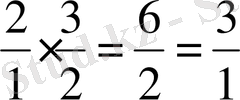 және т. б.
және т. б.
Интервалдарды жартыға бөлу ережесі бізге жарты және ширек дыбысты алуға мүмкіндік береді, бұларды «әлсіз интервалдар» деп атаған. 16
Әл-Фараби былай деп жазады: «Ежелгі грек математиктері үш интервалға бөлінген квартаны «жанр» деп атаған. Бір жанрда үш интервалдың біреуінің қатынасы қалған екеуінің қосындысының қатынасына қарағанда үлкен немесе кіші болуы мүмкін. Интервалдар қатынастары басқа екеуінің қосындысының қатынастарынан үлкен болатын жанрлар «күшті жанр» деп атаған. Керісінше, кіші болған жағдайда «жіңішке жанр» деп атаған».
Плутарх былай деген: «Ұлы Пифагор музыканы сезімге негізделіп бағалауға қарсы болған. Оның пікірінше, музыканың ерекшеліктері ақыл-ой арқылы қабылдануы қажет, сондықтан ол музыканы музыкалық қабілетіне, естуіне, қабылдауына қарап емес, математикалық үйлесім негізінде бағалап, оны оқып-үйренуді бір ғана октавамен шектелу жеткілікті деп тапқан».
Пифагорша музыканың ғылыми негізі төмендегідей құрылған:
- Әр тон өзіне сәйкес санмен өрнектеледі.
- Өзара тең интервалға қатынастары тең сандар сәйкес келеді.
- Үндес интервалдарға (п-1) :п түріндегі эпимерлік және п:1 түріндегі еселік қатынас сәйкес келеді.
- Үндестігі бірдей дыбыстарға, мәселен октаваға п:1 теңдікке жуық келетін 2:1 қатынасы сәйкес келеді.
Екі дыбыстың жағымды, үндес байланысы-консонанс деп аталады, үндес емес, жағымсыз байланыс - диссонанс деп аталады.
Пифогор үндес интервалдар қатарына октава, квинта, кварталарды жатқызған болса, ғұлама ғалым Ибн Сина әл Фарабидің ізімен бұл интервалдарға терцияны да қосады. Сөйтіп, үндес интервалдар саны арта түседі. Бұл Ибн Синаның ұлы жаңалығы еді. Осы жайды айта келіп грузин музыка зерттеушісі Б. А. Гулисашвили: «Терцияны тұңғыш рет ортағасырлық Шығыстың ұлы ойшылдары әл Фараби мен Ибн Сина жасады. Шығыс халықтары өзінің ұлы түлегі әл Фарабиді мақтан тұтуларына әбден болады. Өйткені, ол Батыс Еуропаны екі ғасыр артта қалдырып, жер жүзіне тұңғыш рет терция интервалын үндес (консонанстық) дыбыстар санатына қосты. Ибн Сина болса, Пифагор терциясынан таза терцияға өтудің жолын көрсетті», - деп жазған еді. 17
Ибн Сина консонансқа тән құбылыс 2:1 екенін анықтап: «Осы байланысқа негізделген кез келген екі дыбыс жоғары дәрежедегі үндестікке ие болады», - дейді, мұндай интервалдардың бір дыбысы оның екіншісіне тең. Басқаша айтар болсақ, бірі екіншісінің қосарланған биіктігіне тең болады (прима-октава) . Үндес интервалдардың тек қана өзара тең дыбыстар арқылы емес, басқа да байланыстар арқылы жасалатынын айта отырып, Ибн Сина оларды бес түрге бөлген:
- Екі еселенген
- Бір үлес артық
- Үлестері артық
- Екі еселенген байланыстан бір үлес артық
- Үлестері артық дыбыстар байланысы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz