Мектеп бағдарламасында нақты сандарды оқытудың маңызы мен әдістемесі


Тақырыбы: Нақты сандар
Мазмұны:
КІРІСПЕ . . . 3
І Бөлім Мектеп бағдарламасында нақты сандарды оқытудың маңызы
1. 1. Нақты сандар туралы түсінік . . . 7
1. 2. Мектеп оқушыларының оқу процесінде нақты сандарды меңге-
рудің өзекті мәселелері . . . 9
1. 3. Математика пәнін оқыту үрдісінде нақты сандарды үйретудің рөлі
мен маңыздылығы . . . 13
ІІ Бөлім Мектеп оқушыларына нақты сандарды оқытудың әдістемесі
2. 1. Мектеп оқуышларына нақты сандар туралы ұғымды қалыптастыру-
дың дидактикалық шарттары . . . 17
2. 2. Мектеп оқуышыларына нақты сандарды оқытудың әдістері мен
тиімді жолдары . . . 20
2. 3. Нақты сандар бар есептер жүйесі - оқушылардың математикалық
ұғымдарды меңгерудің басты құралы . . . 24
ҚОРЫТЫНДЫ . . . 27
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР . . . 29
КІРІСПЕ
Елімізде болып жатқан экономикалық өзгерістерге байланысты жалпы білім беру жүйесіне қойылатын талаптар да өзгеруде. Білім беру жүйесі қоғамның әлеуметтік -экономикалық дамуының жетекші рөлін атқаруда. Мектеп оқушылары алған білімен шектеліп қана қоймай, оны ары қарай өздігінен белсенді, нысаналы танымдық іс-әрекетті нәтижесінде игеруі тиіс.
Оны жүзеге асыру оқушылардың белсенділігі мен ізденінімпаздығын ынталандыру септігін тигізетін оқу үрдісін ұйымдастырудың тәсілдерін, әдістері мен нысандарын іздестіруге өзекті сипат береді.
Математика пәні бойынша білім сапасын көтеруде оқушылардың ойлау қабілетін дамыту қалыптасқан, меңгерілген білімге байланысты. Оқу процесіндегі қажетті оқу материалдарын оқушылардың толық меңгеруі үшін әрбір төменгі сынып мұғалімдері логикалық қағидаларды қолданудың тиімді жолдарын қарастыруы қажет. Осындай жаттығуларға бөлінген уақыт жоғарғы сыныптарда өз нәтижесін берері сөзсіз.
Сан ұғымы өте ерте заманда туған. Бұл ұғым туралы ғасырлар бойы кеңейтіліп әрі жалпылана түскен. Өлшеулер жүргізу қажеттілігі оң рационал сандарға әкеп соқтырады. Теңдеулерді шешу теріс сандардың шығуына алып келді. Теріс сандар ұзақ уақыт бойы «жалған» сандар деп есептеліп, «қарыз» («борыш»), жеткіліксіздік («жетімсіздік») ретінде түсіндіріліп келген.
Оң және теріс сандарға амалдар қолдану ережесі ұзақ уақыт бойы тек қосу және азайту жағдайлары үшін ғана қарастырылып отырған. Мысалы, бұл ережені үнді математиктері ҮІІ ғасырда былай тұжырымдаған: «Екі мүліктің қосындысы мүлік болады, екі қарыздың қосындысы қарыз болады, мүлік пен қарыздың қосындысы бұлардың айырмасына тең болады». Тек ХҮІІ ғасырда ғана Декарт пен Ферма енгізген координаттар әдісі пайдаланыла бастағаннан бері теріс сандар оң сандармен тең праволы сандар ретінде қабылданды.
Бүтін және бөлщек сандар рационал сандар жиынын құрайды. Бұл сандар есептеуге қолайлы: екі рационал санның қосындысы, айырмасы, көбейтіндісі және бөліндісі (бөлгіш нөлден өзге сан болғанда) рационал сандар болып табылады. Рационал сандардың тығыздық қасиеті бар, мұның арқасында кез келген кесіндіні, бірлік өлшем ретінде қабылданған кесіндімен кез келген дәлдік дәрежесі бойынша өлшеуге және де өлшеу нәтижесін рационал санмен өрнектеуге болады. Сондықтан рационал сандар ұзақ уақыт бойы азаматтың іс жүзіндегі қажеттіліктерін толық қамтамасыз етіп келді (және де қазіргі кезге дейін қамтамасыз етуде) . Соған қарамастан шамаларды өлшеу мәселесі жаңа сан, иррационал санның шығуына әкеп тіреді.
Рационал және иррационал сандар жиындарының бірігуі нақты сандар жиынын береді және оны R арқылы белгілейді.
Кез келген нақты санды ақырсыз ондық бөлшек түрінде жазуға болады. Егер сан рационал болса, онда бөлшек периодты, егер сан иррационал болса, онда бөлшек периодсыз болады.
Әрбір нақты санға координата түзуінің жалғыз нүктесі және керісінше, координата түзуінің әрбір нүктесіне жалғыз нақты сан сәйкес келеді. Басқаша айтқанда, түзудегі нүктелер жиыны мен нақты сандар жиынының арасында өзара бірмәнді сәйкестік орнатуға болады.
Нақты сандар жиынын сандар түзуі деп те атайды. Сандар түзуінің геометриялық моделі (бейнесі) - координата түзуі.
Ақырлы ондық бөлшектерді қосу, азайту, көбейту және бөлу ережелері бізге белгілі. Ақырсыз ондық бөлшекерге қолданылатын бұл амалдар ережелері шексіз процестерді талап етеді, сондықтан да олар теориялық тұрғыдан ғана маңызды.
Практикада ақырсыз ондық бөлшектерді (нақты сандарды) жуықтап қосады, азайтады, көбейтеді және бөледі.
Оң ақырсыз ондық бөлшектегі үтірге дейінгі санды осы бөлшектің бүтін бөлігі деп атаймыз.
Ақырсыз ондық бөлшектің үтірден кейінгі бірінші цифр осы бөлшектің бірінші разрядының цифры, үтірден кейінгі екінші цифр - екінші разрядтық цифр, үшіншісін - үшінші разрядтық цифр, т. с. с атайды.
Бағдарламалардағы және оқулықтардағы енгізілген кейінгі жылдардағы өзгерістер математика әдістемесін, оның ішінде математикалық ұғымдарды оқыту әдістемесін қайта қарауды және жетілдіруді қажет етеді.
Курстық жұмыстың мақсаты: мектеп бағдарламасында нақты сандарды оқыту.
Курстық жұмыстың зерттеу объектісі: оқушыларға нақты сандар туралы ұғымды қалыптастыру мәселелері.
Курстық жұмыстың зерттеу пәні: оқушыларға нақты сандар ұғымын қалыптастырудың тиімді жолдарын анықтау.
Курстық жұмыстың міндеттері:
- Нақты сандар туралы түсінік;
- Мектеп оқушыларының оқу процесінде нақты сандарды меңгеру-
дің өзекті мәселелері;
- Математика пәнін оқыту үрдісінде нақты сандарды үйретудің рөлі
мен маңыздылығы;
- Мектеп оқуышларына нақты сандар туралы ұғымды қалыптастыру-
дың дидактикалық шарттары;
-Мектеп оқуышыларына нақты сандарды оқытудың әдістері мен
тиімді жолдары;
- Нақты сандар бар есептер жүйесі - оқушылардың математикалық
ұғымдарды меңгерудің басты құралы.
Зерттеу көздері: Зерттеу мәселесі бойынша математика, педагогика ғалымдардың, әлеуметтанушылардың, психологтардың еңбектері; ҚР «Білім беру туралы» Заңы; Елбасшысының халыққа жолдаған «Қазақстан - 2030» үндеуі; «Кәусар бұлақ» бағдарламасы; «Атамекен» бағдарламасы; Қазақстан Республикасында жалпы орта білім беру тұжырымдамасы; ҚР 2015 жылға дейінгі білім беруді дамыту тұжырымдамасының педагогикалық және жас ерекшелігі психологиясы теориялары, ұлттық тәлім-тәрбие туралы ғылыми зерттеулер мен теориялық әдебиеттері негіздеріне сүйеніп жасалған.
Зерттеу әдістері: тақырыпты зерттеу барысында қолданылған педагогикалық және психологиялық әдебиеттерге, ғылыми мерзімді басылымдарға ғылыми талдау жасау, педагогикалық эксперимент өткізу, анкета және интервью әдістері қолданылды.
Курстық жұмыстың құрылымы: курстық жұмыс кіріспеден, екі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспе бөлімінде осы тақырыптың көкейкестілігі, нақты сандарды үйрету мәселелері және оқу-тәрбие процесінің бірізділігі, оны зерттеуге ат салысқан ғалымдардың еңбектерінің құндылығы қарастырылды. Зерттеу жұмысының ғылыми аппараты, мақсаты, міндеттері әдістері объектісі мен пәні көрсетілді.
«Мектеп бағдарламасында нақты сандарды оқытудың маңызы» деп аталатын бөлімде нақты сандар туралы түсінік, мектеп оқушыларының оқу процесінде нақты сандарды меңгерудің өзекті мәселелері және математика пәнін оқыту үрдісінде нақты сандарды үйретудің рөлі мен маңыздылығы қарастырылады.
«Мектеп оқушыларына нақты сандарды оқытудың әдістемесі» деп аталатын бөлімде мектеп оқуышларына нақты сандар туралы ұғымды қалыптастырудың дидактикалық шарттары, мектеп оқуышыларына нақты сандарды оқытудың әдістері мен тиімді жолдары және нақты сандар бар есептер жүйесі - оқушылардың математикалық ұғымдарды меңгерудің басты құралы туралы қарастырылады.
І Бөлім Мектеп бағдарламасында нақты сандарды оқытудың маңызы
1. 1. Нақты сандар туралы түсінік
Сан ұғымы өте ерте заманда туған. Бұл ұғым туралы ғасырлар бойы кеңейтіліп әрі жалпылана түскен. Өлшеулер жүргізу қажеттілігі оң рационал сандарға әкеп соқтырады. Теңдеулерді шешу теріс сандардың шығуына алып келді. Теріс сандар ұзақ уақыт бойы «жалған» сандар деп есептеліп, «қарыз» («борыш»), жеткіліксіздік («жетімсіздік») ретінде түсіндіріліп келген.
Оң және теріс сандарға амалдар қолдану ережесі ұзақ уақыт бойы тек қосу және азайту жағдайлары үшін ғана қарастырылып отырған. Мысалы, бұл ережені үнді математиктері ҮІІ ғасырда былай тұжырымдаған: «Екі мүліктің қосындысы мүлік болады, екі қарыздың қосындысы қарыз болады, мүлік пен қарыздың қосындысы бұлардың айырмасына тең болады». Тек ХҮІІ ғасырда ғана Декарт пен Ферма енгізген координаттар әдісі пайдаланыла бастағаннан бері теріс сандар оң сандармен тең праволы сандар ретінде қабылданды.
Бүтін және бөлщек сандар рационал сандар жиынын құрайды. Бұл сандар есептеуге қолайлы: екі рационал санның қосындысы, айырмасы, көбейтіндісі және бөліндісі (бөлгіш нөлден өзге сан болғанда) рационал сандар болып табылады. Рационал сандардың тығыздық қасиеті бар, мұның арқасында кез келген кесіндіні, бірлік өлшем ретінде қабылданған кесіндімен кез келген дәлдік дәрежесі бойынша өлшеуге және де өлшеу нәтижесін рационал санмен өрнектеуге болады. Сондықтан рационал сандар ұзақ уақыт бойы азаматтың іс жүзіндегі қажеттіліктерін толық қамтамасыз етіп келді (және де қазіргі кезге дейін қамтамасыз етуде) . Соған қарамастан шамаларды өлшеу мәселесі жаңа сан, иррационал санның шығуына әкеп тіреді.
Ежелгі Грецияда пифагордың ( біздің заманымызға дейінгі ҮІ ғасырда) мектебінде, егер өлшеу бірлігі ретінде квадраттың диагоналын рационал санмен өрнектеуге болмайтыны дәлелденген болатын. Квадраттың диагоналы және оның қабырғасы секілді кесінділерді өлшенбейтін кесінділер деп атаған.
Бұдан кейінгі уақытта (біздің заманымызға дейінгі Ү-ІҮ ғасырларда) ежелгі грек математиктері толық квадрат болмайтын кез келген натурал
n
саны үшін
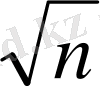 санының иррационалдығын дәлелдеді.
санының иррационалдығын дәлелдеді.
Үндістанның, Таяу және Орта Шығыстың, ал кейініректе Европаның математиктері иррационал шамаларды пайдаланды. Бірақ ұзақ уақыт бұларды тең праволы сан ретінде қабылдамаай келген. Оларды қабылдауға Декарттың «Геометриясының» шығуы ықпал жасады.
Әрбір рационал немесе иррационал сан координаттық түзудің бойында нүктемен кескінделеді, және керісінше, координаттық түзудің бойындағы әрбір нүктеге белгілі бір рационал немесе иррационал, яғни нақты сан сәйкес келеді.
Иррационал сандар енділірілгеннен кейін координаттық түзудің бойындағы барлық «бос орындар» толтырылады. Осы қасиетке сүйненіп, нақты сандар жиыны (рационал сандар жиынынан айырмашылығы) үздіксіз болып табылады делінеді.
Кез келген нақты санды шектеусіз (период немесе периодсыз) ондық бөлшек түрінде көрсетуге болады. ХҮІІІ ғасырда Л:Эйлер (1707-1783) мен И. Ламберт (1728-1777) кез келген шектеусіз ондық бөлшек иррационал сан болатынын көрсетті. Шектеусіз ондық бөлшек негізінде нақты сандар құруды неміс математигі К. Вейерштрасс (1815-1897) жасады. Нақты сандар теориясын мазмұндаудың басқаша тәсілдерін неміс математиктері Р. Дедекинд (1831- 1916) пен Г. Кантор (1845-1918) ұсынды.
1. 2. Мектеп оқушыларының оқу процесінде нақты сандарды меңгерудің өзекті мәселелері
Иррационал (рационал емес) сан деп, ақырсыз периодсыз ондық бөлшек түрінде жазуға болатын санды айтады. Мысалы, 0, 101 10 1110 0 . . . Математикада белгілі бір саны π саны, е саны (натурал логарифм негізі) - иррационал сандар.
Иррационал сан түсінігіне келтіретін мысалды мына теорема береді: «Квадраты 2-ге тең рационал сан жоқ». Басқаша айтқанда, рационал сандар жиынында х
2
-2 = 0 теңдеуін шешу мүмкін емес. Өйткені, бұл теңдеудің түбірлері
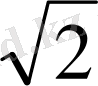 мен -
мен -
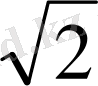 - иррационал сандар.
- иррационал сандар.
Осы сияқты квадраты 5-ке, 7-ге, 10-ға тең рационал сандар жоқ. Квадраты көрсетілген сандарға тең иррационал сандар сәйкес
 ,
,
 ,
,
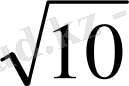 деп белгіленеді. Оларға қарама-қарсы -
деп белгіленеді. Оларға қарама-қарсы -
 , -
, -
 , -
, -
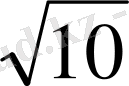 сандары да иррационал сандар.
сандары да иррационал сандар.
Рационал және иррационал сандар жиындарының бірігуі нақты сандар жиынын береді және оны R арқылы белгілейді.
Кез келген нақты санды ақырсыз ондық бөлшек түрінде жазуға болады. Егер сан рационал болса, онда бөлшек периодты, егер сан иррационал болса, онда бөлшек периодсыз болады.
Әрбір нақты санға координата түзуінің жалғыз нүктесі және керісінше, координата түзуінің әрбір нүктесіне жалғыз нақты сан сәйкес келеді. Басқаша айтқанда, түзудегі нүктелер жиыны мен нақты сандар жиынының арасында өзара бірмәнді сәйкестік орнатуға болады.
Нақты сандар жиынын сандар түзуі деп те атайды. Сандар түзуінің геометриялық моделі (бейнесі) - координата түзуі.
Ақырлы ондық бөлшектерді қосу, азайту, көбейту және бөлу ережелері бізге белгілі. Ақырсыз ондық бөлшекерге қолданылатын бұл амалдар ережелері шексіз процестерді талап етеді, сондықтан да олар теориялық тұрғыдан ғана маңызды.
Практикада ақырсыз ондық бөлшектерді (нақты сандарды) жуықтап қосады, азайтады, көбейтеді және бөледі.
Оң ақырсыз ондық бөлшектегі үтірге дейінгі санды осы бөлшектің бүтін бөлігі деп атаймыз.
Ақырсыз ондық бөлшектің үтірден кейінгі бірінші цифр осы бөлшектің бірінші разрядының цифры, үтірден кейінгі екінші цифр - екінші разрядтық цифр, үшіншісін - үшінші разрядтық цифр, т. с. с атайды.
Егер α оң сан болса, онда - α теріс, ал α теріс сан болса, онда - α оң сан болады; α = 0 болса, онда - α = 0 болады.
Α нақты санының модулі немесе абсолют шамасы деп,
егер α оң сан болса, α санының өзін,
егер α нөл болса, нөлді;
егер α теріс сан болса - α санын айтады.
Бұл анықтамадан санның модулі оң сан немесе нөл болатынын көреміз. Мысалы, a =
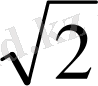 Equation. 3, b = -
Equation. 3, b = -
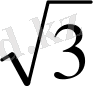 , с = 0 болса, онда:
׀ а ׀
=
, с = 0 болса, онда:
׀ а ׀
=
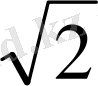 ,
׀
b
׀
= -
,
׀
b
׀
= -
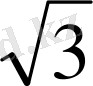 ,
׀ с ׀
=
0.
,
׀ с ׀
=
0.
Нақты сандарды салыстыруға тоқталайық:
Екі ақырсыз ондық бөлшек сандарды берілсін ( екеуінің де периоды 9 емес деп санаймыз) . Оларды салыстыру үшін келесі ережелерді қолдануға болады.
1-ереже. Егер екі нақты санның таңбалары бірдей болып олардың модульдерінің бірдей бүтін бөліктері және сәйкес разрядтарының бірдей цифрлары бар болса, онда олар тең болады.
Бірақ нөл саны үшін:
0 = 0, 000 . . . = - 0, 000 . . . = + 0, 000 . . .
болатынын еске саламыз.
2-ереже. Теріс сан 0-ден кіші және кез келген оң нақты саннан кіші. 0-саны кез келген оң нақты саннан кіші.
3-ереже. Екі оң нақты сандардың қайсысының бүтін бөлігі үлкен болса сонысы үлкен. Ал, егер бүтін бөліктері бірдей болса, онда цифрлары әртүрлі болатын ең кіші разрядына қараймыз; қайсы санның осы разрядының цифры үлкен болса, сол сан үлкен.
Теріс нақты сандар үшін бәрі керісінше: олардың қайсысының модулі кіші болса, сонысы үлкен болады.
Егер а мен b нақты сандары тең болса, онда а = b деп жазады. Егер де а саны b-дан кіші болса, онда а < b немесе b > а деп жазады, а саны b-ға тең емес болса, оны а ≠ b деп жазады.
Мысалы: -3, 1 мен - 3(1) сандарын салыстыру керек:
׀-3, 1׀ = 3, 1 =3, 1000 . . . ; ׀ -3, (1) ׀ =3, (1) = 3, 111 . . . ;
3, 1 <3, (1) болғандықтан -3, 1 >-3, (1) болады (3-ереже) .
Жоғарыдағы айтылған ережелерді геометриялық тұрғыдан былайша айтуға болады:
Берілген екі санның координаталар түзуінде қайсысы оң жағында орналасса сонысы үлкен (оң жай бөлшектерді салыстыру ережесін §2, 12п. қараңыз) .
<, > - қатаң теңсіздік таңбалары, ал ≥, ≤ - қатаң емес теңсіздік таңбалары.
а ≤ b жазуы «а саны b-дан кіші немесе а саны b-ға тең» деген айтылымдардың ең болмағанда біреуінің дұрыс екенін білдіреді (а ≤ b жазуын - «а саны b-дан үлкен емес» - деп те оқиды) . Мысалы, 3 ≤ 5, 5 ≥ 5 дұрыс теңсіздіктер.
а ≥b болса, онда а-ны теріс емес сан деп театайды.
Егер а < b және b< с болса, онда а < b < с жазуы (қос теңсіздік) қолданылады.
Кез келген a, b, c, d нақты сандар үшін келесі қасиеттер орындалады
1 0 . а < b болса, онда а < b < с болатындай с саны табылады.
2 0 . а < b және b< с болса, а < с болады (теңсіздіктердің транзитивті (алмасымдылық) қасиеті) ;
3 0 . Егер а < b болса, а+с < b +с;
4 0 . Егер а < b болса, онда кез келген с > 0 саны үшін ас < bс;
5 0 . Егер а < b және с< 0 болса, онда ас > bс;
6 0 . Егер а < b және с< d болса, онда а+с < b +d;
7 0 . Егер a, b, c, d - оң сандар болып, а < b және с< d болса, онда ас < bd;
8 0 . Егер а < b және с > d болса, с-а > d- b ;
9 0 . Егер а > b > 0 болса, онда ;
10 0 . Егер а > b > 0 болса, онда кез келген натурал n саны үшін а n > b n теңсіздігі орындалады.
Нақты сандар үшін орындалатын амалдар ережесіне тоқталып көрейік:
Таңбалары бірдей екі санның қосындысын табу үшін олардың модульдерін қосып, қосынды алдына қосылғыштардың таңбасы жазылады. Мысалы,
(+12) + (+8) = +20; (-12) +(-8) = -20.
Таңбалары әртүрлі екі санның қосындысын табу үшін қосылғыштардағы үлкен модульден кіші модульді шегеріп, айырма алдына модулі үлкен санның таңбасын жазады. Мысалы,
(+12) + (-8) = + (12-8) = 4; (-12) + (+8) = - (12-8) = -4.
Бір саннан екінші санды шегеру үшін, азайтқышқа қарама-қарсы санды азайғышқа қосады. Мысалы,
12- (-8) = 12+(+8) = 20; 12- (+8) = 12+ (-8) = 4.
Екі санның көбейтіндісі (бөліндісін) табу үшін ол екі санның модульдерін көбейтеді де (бірінші санның модулін екінші санның модуліне бөледі де), көбейтінді (бөлінді) алдына - егер екі сан бірдей таңбалы болса, «+», ал әртүрлі таңбалы болса «-» таңбасын жазады. Мысалы,
(-12) * (-8) = +12* 8 = 96; (-24) /(+3) = - 24/3 = -8.
1. 3. Математика пәнін оқыту үрдісінде нақты сандарды үйретудің рөлі мен маңыздылығы
Иррационал сан ұғымы түбір табуға,
кесіндінің ұзындығын өлшеуге және кейбір
функцияларды зерттеуге байланысты пайда
болған. Иррационал сөзі латынның irrationalis-
ақылға -ойға сыймайтын, негіздеуге болмай-
тын көмегімен санап шығуға болмайтын)
деген сөзінен шыққан.
Шамаларды, атап айтқанда, ұзындықты өлшеу үшін рационал сандар қоры жеткіліксіз болады. Мысалы, қабырғасы өлшем бірлігіне тең болатын шаршы диагоналінің ұзындығын ешқандай рационал санмен өрнектеуге болмайды.
Шаршының диагоналі мен қабырғасы өлшемдес емес, яғни ұзындықтың бірлігі ретінде шаршыны қабырғасын алсақ, онда осы шаршының диагоналінің ұзындығын оң рационал сан арқылы өрнектеуге мүмкін болмайды.
Дәлелдеу: Қарсы жоримыз, яғни қабырғасы е болатын шаршының диоганалін
 m/n бөлшегімен өрнектеледі деп есептейік:
m/n бөлшегімен өрнектеледі деп есептейік:
а = (m/n)
 Equation. 3 Пифагор теоремасы бойынша е
2
+ е
2
=а
2
=( (m/n)
Equation. 3 Пифагор теоремасы бойынша е
2
+ е
2
=а
2
=( (m/n)
 Equation. 3 )
2
немесе 2е
2
= (m
2
/n
2
)
Equation. 3 )
2
немесе 2е
2
= (m
2
/n
2
)
 2
немесе m
2
/n
2
= 2. Бұдан m
2
= 2n
2,
яғни m немесе m - жұп сан. Сондықтан оны былай жазамыз: m = 2k.
2
немесе m
2
/n
2
= 2. Бұдан m
2
= 2n
2,
яғни m немесе m - жұп сан. Сондықтан оны былай жазамыз: m = 2k.
Ендеше, 4k 2 = 2n 2 немесе n 2 = 2k 2 . Соңғы теңдікпен n саны да жұп сан деген қорытынды жасауға болады, яғни n = 2p.
Сөйтіп, m/n бөлшегінің алымы да, бөлімі де жұп сан болып отыр, демек олардың ортақ бөлімі бар, былайша айтқанда, m/n қысқартылмайтын бөлшек.
Ал, бұл біздің ұйғаруымыға қарама-қайшы келеді. Тағайындалған қарама-қайшылық, ұзындығын рационал санмен өрнектеуге болмайтын кесінділердің бар болатындығын дәлелдейді. Бұл сан жиындарын одан әрі кеңейтудің қажеттігі туралы қорытынды жасауға келтіреді. Бұған дейін қарастырылған және құрылған рационал сандарды тегі жаңа иррационал сандармен толықтыру керек болады.
Осы сандардың көмегімен ұзындықтың таңдап алынған өлшем бірлігімен өлшемдес болмайтын кесіндінің ұзындығын өрнектеуге болады. Егер кесіндінің ұзындығы ұзындықтың таңдап алынған өлшем бірлігімен өлшемдес болса, онда өлшеудің нәтижесі рационал санмен өрнектеледі.
Олай болса, кез келген кесіндінің ұзындығын, жалпы алғанда кез келген скляр шаманы өлшеу нәтижесі не рационал санмен, не иррационал санмен өрнектеледі.
Бізге бұрыннан белгілі болғанындай оң рационал сандарға амалдар қолдану, олар ондық бөлшек түрінде жазылған жағдайда қолайлы болады. Сондықтан шамаларды өлшеу нәтижесін де, нақтырақ айтқанда кесіндінің ұзындығын өлшеу нәтижесін ондық бөлшек түрінде жазып көрсеткен тиімді.
Айталық, е- ұзындық бірлігі, ал а ұзындығы өлшенетін кесінді болсын және де а кесіндісі әрқайсысы е-ге тең n кесінділер мен е- ден қысқа а 1 кесіндіден тұратын болсын, яғни nе < а < (n+1) . Сонда n және n+1 сандары а кесіндісінің ұзындық бірлігі е болғандағы бірлікке дейінгі дәлдікпен кемімен және артығымен алынған жуық мәндері болып табылады.
Жауапты жоғары дәлелдікпен алу үшін е кесіндісінің оннан бір бөлігіне тең болатын е 1 кесіндісін алып, оны а 1 кесіндісі бойына саламыз. Мұнда екі жағдайы болуы мүмкін:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz