Қалыпты таралу заңы

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

Жоспар

Гистограммалар және кездейсоқ ауытқулардың таралу заңдары

1 Қалыпты таралу заңы

2 Стъюденттің t - таралу заңы

3 Пирсонның χ ² - таралу заңы

4 Фишердің таралу заңы

5 Кездейсоқ ауытқуларды түрлендіру

Негізгі әдебиеттер:

Гистограммалар және кездейсоқ ауытқулардың таралу заңдары

Өлшем нәтижелері мен олардың кездейсоқ қателері кездейсоқ ауытқулар болатындықтан олардың таралулары әртүрлі заңға бағынады.

Кездейсоқ ауытқулардың таралуының мынадай түрлері бар: біркелкі таралу, қалыпты таралу, Стъденттің t - таралуы, Пуассон таралуы, Фишердің F - таралуы, Пирсонның χ ² - таралуы (хи - квадрат таралуы), т. б.

1 Қалыпты таралу заңы

Таралудың практикада жиі қолданылатын түрі Гаусстың қалыпты таралуы. Қалыпты таралу басқа таралуларға қарағанда теориялық жағынан кеңінен зерттелінген. Кездейсоқ ауытқулардың қалыпты таралуы Гаустың қалыпты таралу заңына бағынады. Гаусс заңы әртүрлі заңмен таралатын шамалар үшін ең шекті заң болып табылады, басқа сөзбен айтқанда, әр түрлі таралатын кездейсоқ ауытқулардың таралуы ақырғы шегінде Гаусс заңына бағынады (Ляпунов теоремасы) .

Қалыпты таралудың дифференциалдық функциясының математикалық өрнегі мына түрде жазылады:

мұнда φ(х) - ықтималдық тығыздығы; Х - кездейсоқ ауытқуның мәні (сол шама үшін φ(х) анықталады) ; а = М(Х) - математикалық күтім; σ - орташа квадраттық ауытқу (а және σ - таралу параметрлері) .

Қалыпты таралу тығыздығының графигі қалыпты қисық немесе Гаусс қисығы деп аталады (1 - сурет) .

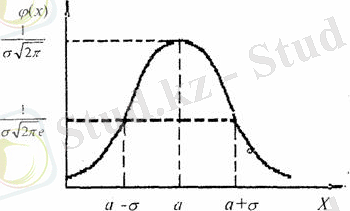
1 - сурет. Гаусс қисығы

Мұнда жүйелі қателер есептеулерден толығымен шығарылып тасталады; сондықтан шаманың шын мәні өлшем нәтижелерінің математикалық күтіміне тең болады. Сонда абсциссаның математикалық күтімге тең мәні (а нүктесі) таралу центрі деп аталады.

Қалыпты таралу қисығының қасиеттері:

1. Таралу қисығы симметриялы қисық; қисықтың симметриялы болуы мәндері бірдей, бірақ таңбалары әртүрлі ауытқулардың ықтималдықтары бірдей болатынын көрсетеді.

2. Қисықтың максимум нүктесі бар; оның мәні 1/σ тең және екі иілу нүктесі бар, олардың абсциссалары а - σ және а + σ, ординаталары 1/σ е.

3. Х - тың мәндері шексіздікке ұмтылған сайын (х → ∞) қисықтың екі ұшы Х өсіне қарай асимптотикалық жақындайды.

Қисықтың Х өсінің бойындағы орны а параметрінің өзгеруімен өзгереді, ал формасы (қалыпты түрі) σ параметріне байланысты өзгереді. Демек, Гаусс қисығының түрі екі параметрмен, яғни математикалық күтім және стандартты ауытқумен анықталады.

2 Стъюденттің t - таралу заңы

Статистикалық зерттеулерде, сондай - ақ, химиялық эксперимент нәтижелерін математикалық өңдеуде кездейсоқ ауытқуның таралуы қалыпты таралу болғанымен оның сұрыптама жиынтығы бас жиынтықты көрсете алмайтыны, яғни сұрыптама көлемі (n) аз болатыны жиі кездеседі. Мұндай жағдайларда бас параметрлерді дәл анықтауға болмайтындықтан, эксперимент нәтижелерін статистикалық өңдеу үшін сұрыптамалық параметрлерді қолдану қажет болады. Математикалық статистиканың кіші сұрыптамаларды (2 < n < 20) өңдеуге қолданылатын бөлімін шартты түрде макростатистика деп атайды.

Қалыпты таралатын кездейсоқ ауытқуларды макростатистикалық өңдеу Стъюденттің t - таралу заңына негізделген (Стъюдент - ағылшын математигі В. С. Госсеттің бүркеншік аты, бұл заңды ол 1908 жылы ашқан) .

Кездейсоқ t - шамасын қарастырайық, ол мына өрнекпен берілсін:

(а)

мұнда ξ - қалыпты таралатын кездейсоқ ауытқу; χ - «хи - квадрат» заңы (Пирсон χ ² - таралу заңы) бойынша таралатын кездейсоқ ауытқу. Ал t шамасының таралуы Стъюдент таралуы деп аталады, оның еркіндік дәрежесі n - ге тең. Стъюдент таралуының тығыздығы (дифференциалдық функциясы) мына теңдеумен анықталады:

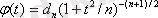(б)

мұнда d _n - тұрақты шама, оның мәні ықтималдық интегралы 1 - ге тең болуына байланысты.

Стъюдент таралуының кестесі жасалынған (Қосымша В. 3 - кесте) . Кестеде берілген мәліметтерді пайдаланып, өлшем нәтижелерін статистикалық өңдеуге, өлшемнің қатесін және оның таралу түрін анықтауға болады.

Стъюдент таралу заңын қалыпты таралатын кездейсоқ Х шамасының математикалық күтімін М(Х) анықтауға қолдануды қарастырайық. Х - тің өлшенген мәндері х ₁ , х ₂ , х ₃ , . . . , х _n , бірақ оның таралу параметрлері (М(Х) және σ ² ) белгісіз болсын. Бұл жағдайда (а) - теңдеуді мына түрде жазуға болады:

(в)

мұнда 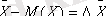; Стъюдент бөлшегі деп аталатын бөлшегінің таралу тығыздығы (б) - теңдеумен өрнектеледі, мұнда f = n - 1 шамасы сұрыптаманың еркіндік дәрежесі; (в) - теңдеудегі және S шамаларын тәжірибелік мәліметтер бойынша есептейді, бұл шамаларды математикалық күтім мен орташа квадраттық ауытқудың нүктелі бағаланулары деп атайды.

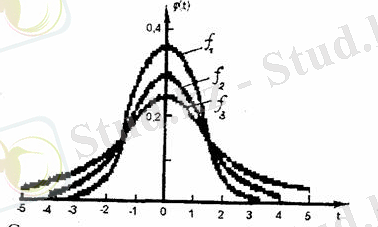
7 - сурет. Стъюдент таралуы бойынша еркіндік дәрежесінің әртүрлі мәндеріндегі (f ₁ > f ₂ > f ₃ ) ықтималдық тығыздығының (φ (х) ) сенімді аралыққа тәуелділігі

3 Пирсонның χ ² - таралу заңы

Стъюдент таралуымен қатар, таралудың тағы бір түрі - Пирсонның «Хи - квадрат» (χ ² ) таралуы қалыпты таралумен байланысты. Кездейсоқ тәуелсіз Х ₁ , Х ₂ , . . . Х _n шамаларының параметрлері: М(Х) = 0 және σ = 1 дейік. Кездейсоқ χ ² шамасын алайық, ол жоғарыдағы шамалардың квадраттарының қосындысына тең болсын:

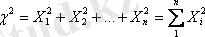
Бұл кездейсоқ ауытқуның таралуын еркіндік дәрежесі n - ге тең χ ² - таралу деп атайды; χ ² - таралудың математикалық күтімі М(Х) = n, дисперсиясы σ = 2n, ал дифференциалдық функциясы (ықтималдық тығыздығы) мына түрде беріледі:

мұнда С _n - тұрақты шама, оның мәнінде мына интеграл 1 - ге тең:

Таралу қисығы бір ғана параметрмен, яғни еркіндік дәреже санымен (n) анықталады; 8 - суретте n - ның үш түрлі мәндері үшін таралу қисығы берілген.

Таралу қисықтары асимметриялы (симметриялы емес) қисықтар. Қисықтардың асимметриясы n саны өскен сайын азайып, n - нің үлкен мәндерінде қалыпты қисыққа айналады.

8 - сурет. χ ² - таралудың ықтималдық тығыздығы

Қалыпты таралатын кездейсоқ ауытқулардың дисперсиясын анықтау. Қалыпты таралатын кездейсоқ ауытқуның бас жиынтығының дисперсиясын (σ ² ) оның сқрыптамалық жиынтығының дисперсиясы (S ² ) арқылы анықтауға болады. Сұрыптамалық дисперсияның таралуын χ ² - таралу бойынша анықтайды.

Берілген Х ₁ , Х ₂ , . . . Х _n сұрыптамасы бойынша алынған мына қосындының

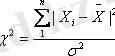(а ^/ )

таралуы «Хи - квадрат» таралу деп аталады, оның еркіндік дәрежесі n - ге тең.

Сұрыптамалық дисперсияны мына формуламен анықтайтынымыз белгілі:

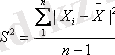
олай болса (а ^/ ) - формуланы былай жазуға болады:

(б ^/ )

Бас жиынтық дисперсияның сенімді аралығын анықтау үшін χ ² - таралудың кестесін пайдаланады.

Жоғарыдағы (б ^/ ) - өрнектен:

мұнда

Кестеден γ ₁ және γ ₂ - ні табамыз, олардың мәндері арқылы мына теңдіктер жазылады:

р(γ ₁ S < σ) = α ₁ ,

р(γ ₂ S > σ) = α ₂

демек, χ ² - таралуы симметриялы емес болатындықтан, мәндері бірдей, бірақ таңбалары әртүрлі қателердің ықтималдықтары да әртүрлі болады (яғни α ₁ ≠ α ₂ ) . Ал α ₁ = α ₂ жағдайда γ ₁ ≠ γ ₂ екенін көріп отырмыз. Әдетте мына түрде жазылған өрнек қолданылады:

р(γ ₁ S < σ < γ ₂ S) = α.

Мысал келтірейік:

Бес параллель өлшемнің орташа квадраттық қатесі S = 2. Сенімді ықтималдықты 0, 95 деп алып, σ - ның сенімді аралығын анықтау керек.

Шешуі:

Кестеден n = 5, α = 0, 95 болғанда γ ₁ = 0, 599, γ ₂ = 2, 87 екенін табамыз, содан σ - ның сенімді аралығы: 0, 599·2 < σ < 2, 87·2 немесе 1, 2 < σ < 5, 7. Бұдан σ - ның мәні жататын шекаралар өте кең және асимметриялы екенін көреміз.

4 Фишердің таралу заңы

Мәселен, Х ₁ және Х ₂ дейтін кездейсоқ екі тәуелсіз шаманың таралуы χ ² - таралу заңына бағынсын; еркіндік дәрежелері f ₁ және f ₂ болсын дейік. Бұл шамалардың мынадай қатынасын F деп белгілейік:

Сонда F - шамасының таралуын Фишердің F - таралуы деп атайды. Фишер таралуының еркіндік дәреже сандары f ₁ және f ₂ , дифференциалдық функциясының (φ(F) ) математикалық өрнегі өте күрделі, математикалық күтімі М(Х) = f ₁ /f ₂ - 2, дисперсиясы

мұнда f ₂ > 4.

Фишер таралуы еркіндік дәреже сандарымен анықталады; еркіндік дәреженің f ₁ = 10, f ₂ = 50 және f ₁ = 10, f ₂ = 4 мәндеріне сәйкес екі таралу қисықтары 9 - суретте берілген, одан қисықтардың симметриялы емес екенін көреміз.

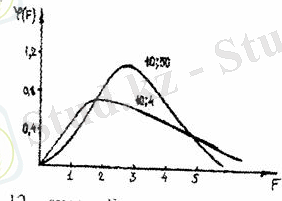
9 - сурет. F - таралу тығыздығы

F - функциясының f ₁ мен f ₂ - нің белгілі мәндерінде және β ₁ = 0, 05, β ₂ = 0, 01 мәнділік деңгейлерге сәйкес келетін мәндері қосымшаның 5 - кестесінде берілген (Қосымша В. 5 - кесте) . Бұл мәндерді кризистік мәндер (F _кр ) деп атайды.

5 Кездейсоқ ауытқуларды түрлендіру

Кездейсоқ ауытқулардың сапалы бағаларын алу үшін ЕКӘ-нің алғашқы шарттарының орындалуы белгілі бір дәрежеде маңызды рөл атқарады.

Олардың кестедегі ең маңыздыларының бірі: кездейсоқ ауытқулар қалыпты кездейсоқ ауытқулар, математикалық күтулері 0-ге тең тұрақты дисперсиядан тұрады, және бірімен-бірі тәуелсіз болады:

( ~ N(0, ) ; cov( , ),

( i ≠ j, i, j = 1, 2, . . . , n) .

Бұл алғашқы шарттар орындалмаған жағдайда, ЕКӘ бойынша алынған бағалаулар аталған қасиеттерге ие бола алмайды және оларға жасалынған тестер сапасыз болады.

Бірдей логарифмдеудің қажеті болмаған жағдайда (аддивті кездейсоқ мүшелер деп), ЕКӘ алғышарттары орындалады, олай болса бағалауға байланысты проблема туындайды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.