Тілдер және автоматтар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 24 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
С. АМАНЖОЛОВ АТЫНДАҒЫ ШЫҒЫС ҚАЗАҚСТАН МЕМЕЛЕКЕТТІК УНИВЕРСИТЕТІ

Қадырова А.С., Сайларбек С.

АВТОМАТТАР ТЕОРИЯСЫ
әдістемелік құрал

Өскемен
С. Аманжолов атындағы ШҚМУ баспасы
2006
УДК 004(072)

Қадырова А.С, Сайларбек С. Автоматтар теориясы: Әдістемелік құрал
А.С. Қадырова, С.Сайларбек; ШҚМУ. – Өскемен: С. Аманжолов атындағы ШҚМУ
баспасы, 2006. – 30 бет.

Әдістемелік құралда автоматтар теориясындағы негізгі түсініктер
қарастырылған; автоматтардың жіктелу түрлері берілген; бағдарламалау
тәжірибесінде қолданылатын автоматтар синтезі сипатталынған. Құралдың
мазмұны – өз бетімен оқуға нұсқалған жеткілікті деңгейдегі дәрістік
материалдар.

Әдістемелік құрал ретінде С. Аманжолов атындағы ШҚМУ – дың
Математика, физика, техника және ақпараттық технологиялар факультетінің
әдістемелік кеңесінде 06.04.06 ж. бекітілді ( № 4 хаттама).

Пікір жазған:
ф.-м.ғ.д., профессор Хисамиев Н.Г.

КІРІСПЕ

Қазіргі кезде ақырлы автоматтарды бағдарламалауда қолдану қайтадан
өрби түсуде, мысалы логикалық басқару аймағы мен объектілі – бағыттлаған
бағдарламалауда. Мур және Мили ақырлы автоматтарын тағайындалуы жалпы
бағдарламалауда қолдану ұсынылады. Сонымен қатар ақырлы автоматтарды
қолданудың бір сұрағы болып әртүрлі трансляторлардағы алгоритмдік тілдердің
синтаксикалық анализі болып табылады. Атақты қолдануларда автоматтардың
кіру ақпаратын есептеу үрдісі сәйкес, іске асыратын автоматтың, бағыныңқы
бағдарламалар мен мысалдардың шегіне шығарылды.
Берілген әдістемелік құралда, оқып–үйренуге автоматтар теориясындағы
негізгі түсініктер ұсынылады. Әдістемелік құралдың негізгі мақсаты –
автоматтар теориясындағы негізгі түсініктермен танысу. Тілдер мен
автоматтар теориясы пәнін алғаш оқығанда студенттер оқу материалының қиын
тілде жазылғанын байқайды және ондағы түсініктер үшін терминдердің жиыны
өте көп қолданылады. Сондықтан құралды жасау барысында авторлар негізгі
түсініктер мен студенттерге қажет негізгі материалдарды қатаң мазмұнын
сақтай отырып, түсінікті әрі ұғынықты тілмен жеткізген.
Әдістемелік құралды жазуда әдебиеттер мен монографиялар кеңінен
қолданылған, олар әдебиеттер тізімінде көрсетілген. Құралдың мәтінінде ол
әдебиеттерге арнайы сілтеме қойылмаған.
Әдістемелік құрал 050602 Информатика мамандықтарының студенттеріне
арналған.

1 АВТОМАТТАР ТЕОРИЯСЫ

1.1 Автомат түсінігі. Автоматтардың түрлері

Автомат – бұл қандай да бір жиынды анықтайтын алгоритм, мүмкін болған
жағдайда ол жиынды басқа жиынға түрлендіруі мүмкін. Автоматтардың
формальсыз сипатталынуы келесі түрде болады: автомат кіру лентасынан,
күйдің нөмірін сақтайтын ақырлы жадысы бар басқару құрылғысынан тұрады,
сонымен қатар көмекші және шығыстық лентасы болуы мүмкін. Автоматтардың екі
типі бар:
1) танығыштар – шығыссыз автоматтар, олар кіру тізбегі берілген L
жиынына тиісті ме соны таниды;
2) түрлендіргіштер – шығысы бар автоматтар, олар x ∈ L шарты
орындалғанда кіру тізбегі х –ті у тізбегіне түрлендіреді.
Кіру лентасын ұяшықтардың сызықтық тізбегі ретінде қарастыруға
болады, әрбір ұяшық ақырлы кіру алфавитінің бір символын сақтай алады.
Автоматтың лентасы шексіз, бірақ әрбір уақыт моментінде ұяшықтардың
тек ақырлы саны ғана бос емес болады. Бос емес аймақтың шекаралы оң және
сол жақтағы ұяшықтары арнайы соңғы маркерлерді алуы мүмкін. Маркер лентаның
тек бір жақ соңында ғана тұруы немесе мүлдем болмауы мүмкін.
Кіру бас тиегі әрбір уақыт моментінде кіру лентасының бір ұяшығын
оқиды. Автоматтың бір жұмысының тактісінде енгізу бастиегі бір ұяшық оңға
жылжуы немесе бір орында тұруы мүмкін, мұндайда ол тек қана оқуды
орындайды, яғни автоматтың жұмыс істеу барысында кіру лентасының
ұяшықтарындағы символдар өзгермейді.
Жұмыс лентасы - ақпаратты сақтаудың көмекші қоймасы. Ондағы
берілгендер автоматтың көмегімен оқылады және оған жазылуы да мүмкін.
Басқару құрылғысы – автоматтың тәртібін басқаратын бағдарлама. Ол
кіру бастиегімен оқылатын ағымды кіру символына сәйкес күйдің және жұмыс
лентасынан алынып тасталған ағымды ақпараттың қалай өзгеретінін
сипаттайтын, бейнелеуі бар күйлердің ақырлы жиынын береді Басқару құрылғысы
жұмыс бастиегінің жылжу бағытын және жұмыс лентасына қандай ақпарат жазу
керектігін анықтайды. Автомат жұмыс тактілерінің қандай да бір тізбегін
орындай отыра жұмыс істейді. Тактінің ең басында кіру символы оқылады және
жұмыс лентасындағы ақпарат зерттеледі. Одан кейін оқылған ақпарат пен
ағымды жағдайға байланысты, автоматтың іс - әрекеті анықталады:
1) кіру бастиегі оңға жылжиды немесе бір орында тұрады;
2) жұмыс лентасына қандай да бір ақпарат жазылады;
3) басқару құрылғысының жағдайы өзгереді;
4) шығу лентасына (егер ол бар болса) символ жазылады.
Автоматтың жұмыс істеу тәртібін автоматтың конфигурациясы терминімен
сипаттаған ыңғайлы, ол келесіден тұрады:
а) басқару құрылғысының жағдайы;
б) кіру лентасындағы берілгендер кіру бастиегінің жағдайымен бірге;
в) жұмыс лентасындағы берлігендер кіру бастиегінің жағдайымен бірге;
г) шығу лентасындағы берілгендер, егер ол бар болса.
Басқару құрылғысы детерминделмеген болуы мүмкін. Мұндай жағдайда
әрбір конфигурация үшін тактілердің ақырлы жиыны бар болуы мүмкін, оның
әрқайсысын автомат осы конфигурациядан шыға отыра жасайды. Басқару
құрылғысы детерминделген болады, егер әрбір конфигурация үшін тек бір ғана
келесі такт мүмкін болса.
Автоматтардың келесі типтері болады: 1) Тьюринг машинасы (ТМ); 2)
сызықты – шектелген автомат (США); 3) магазиндік жадысы бар автомат (МЖ-
автомат); 4) ақырлы автомат (АА).
Ақырлы автоматтың күрделігін автоматтың күрделілігі анықтайды.
Мысалы:
1) Тьюринг машинасы екі жаққа да шексіз ленталардан тұрады;
2) сызықты – шектелген автоматтарда жұмыс лентасының ұзындығы кіру
тізбекшесінің ұзындығының сызықтық функциясын береді;
3) МЖ-автоматта жұмыс лентасы LIFO магазинінің принципімен жұмыс
істейді;
4) ақырлы автоматтарда жұмыс лентасы болмайды.

1.2 Автоматтың формальды анықтамасы

Инициалданбаған автомат – бұл А = (К, X, Y, δ, γ) түрдегі бестік,
мұндағы К – күйлердің жиыны (күйлердің алфавиті); Х – кіру алфавиті; Y –
шығу алфавиті; δ – К: Х→К бейнелеуді беретін өту функциясы; γ – К: Х→У
бейнелеуді беретін шығу функциясы.
Автоматтың функцияларын келесі түрдегі командалардың жиыны ретінде
беруге болады: qx → py, мұндағы q және p ∈ K, x ∈ X, y ∈ Y.
ti қайсыбір тактісінде басқару құрылғысы q жағдайда болсын, ал кіру
лентасынан x символы оқылсын делік. Егер командалардың жиынында qx → py
командасы бар болса, онда ti тактісінде шығу летасына у символы жазылады,
ал келесі ti +1 тактісінде басқару құрылғысы р жағдайына өтеді, яғни:
y(t) = γ(q(t), x(t)), q(t-1) =δ(q(t), x(t)).
Егер qx → py командасы болмаса, онда автомат бұғатталады және ti
моментінде қабылданған символға ешқандай әсер білдірмейді, сонымен қатар
уақыттың келесі моментіндегі символдарды да қабылдамайды.
Инициалданбаған автоматтың анықтамасына сәйкес, жағдайдың алғашқы
сәтінде автомат ерікті болуы мүмкін.
Егер қандай да бір алғашқы жағдай алдын – ала бекітілген болса, онда
мұндай автоматты инициалданған автомат деп атайды, яғни q(0) = q0.
Инициалданған автомат – бұл А = (К, X, Y, δ, γ, q0) түріндегі
алтылық, мұндағы К – жағдайлардың жиыны (жағдайлардың алфавиті); Х – кіру
алфавиті; Y – шығу алфавиті; δ - өту функциясы (К: Х → К бейнелеуі); γ –
шығу функциясы (К: Х → У бейнелеуі); q0 – алғашқы жағдай.

2 ТАНЫҒЫШТАР

2.1 Тілдер және автоматтар

Грамматикалық бөлшектеудің тапсырмасы берілген грамматикадағы
тізбекшенің қорытындысын табу және осы тізбекшенің қорытынды ағашын анықтау
болып табылады.
Тілдер екі түрлі әдіспен берілуі мүмкін:
1) граматикалармен (тілдің әдісін туғызатын);
2) автоматтармен (тілдің әдісін танитын).
Күрделіліктеріне қарай жіктелетін автоматтарға әртүрлі типті тілдер
сәйкес келеді. Автоматтардың қарапайым типі ақырлы автоматтар болып
саналады.
Ақырлы автомат әрбір такт кезінде бір кіру символы есептелінетін кіру
лентасынан тұрады. Кіру лентасына қатысты қайтарымға рұқсат берілмейді.
А = (К, ∑, δ, p0, F) түріндегі бестік ақырлы автомат деп аталады,
мұндағы:
К – күйлердің ақырлы жиыны;
∑ - алфавит;
δ - өту функциясы;
p0 – алғашқы жағдай;
F – қорытынды күйлердің жиыны.
Автоматты күйлерден, лентадан немесе бірнеше ленталарда жазылатын
(оқылатын) символдардың және командалардың топтары арқылы формальды жүйе
ретінде қарастыруға болады.
Ақырлы автоматты граф, өту кестесі, команда және өту матрицасы
түрінде елестетуге болады.

2.2 Реттелетін жиындар

Реттелетін жиындар тілдердің класын береді, олар формальды тілдердің
теориясында маңызды роль атқарады. Әрқайсысы реттелетін жиынды анықтайтын
тілдердің берілуінің бірнеше әдісін қарастырайық. Олардың ішінде –
реттелетін өрнек, оң сызықты грамматикалар, детерминерленген және
детерминерленбеген ақырлы автоматтар.
Σ – қандай да бір алфавит болсын. Σ алфавитіндегі реттелетін жиындар
рекурсивті түрде келесідей анықталады:
1) 0 – бос жиын;
2) {ε} – бос тізбекшелердің жиыны;
3) {a} - a ∈ Σ әрбір элементі үшін реттелетін жиын;
4) егер P және Q - Σ алфавитіндегі реттелетін жиын болса, онда
келесілер де реттелетін жиындар болады:
а) P ∪ Q
б) PQ
в) P*.
Σ – де басқа реттелетін жиындар жоқ. Олай болса Σ берілген
алфавитіндегі тізбекшелердің жиыны реттелетін деп аталады, сонда және тек
қана сонда, егер ол келесі жиындардың бірі болатын болса: 0, {ε} немесе {a}
қандай да бір a ∈ Σ үшін, немесе оны осы жиындарға операциялардың ақырлы
санын - біріктіру, конкатенация және итерация қолдана отырып алуға болады.
Әрбір реттелетін жиын үшін осы жиынды белгілейтін кем дегенде бір
реттелетін өрнек бар болады.
Ақырлы автоматпен танылатын тіл – ол автоматпен алғашқы күйден
қорытынды күйдің біреуіне өткенде оқылатын тізбекшелердің жиыны:
L(A)={a1 a2 ... as p0a1 → p1, p1a2 → p2, ..., p s-1 as → ps; ps ∈
F}.
Жиын реттелетін деп аталады, егер оны танитын ақырлы детерминерленген
автомат бар болса.

2.3. Реттелетін тілдерге операциялар қолдану

Ерікті ақырлы автоматқа сөзсіз детерминерленген ақырлы автомат сәйкес
келеді, ақырлы автоматтарға операциялар қолдану реттелетін жиындарға немесе
реттелетін тілдерге операциялар қолданумен эквивалентті.
Ерікті автоматқа бастапқы және соңғы күйлерде циклсіз эквивалентті
автомат құрастыруға болатыны белгілі.
Теорема. Ерікті ақырлы автомат үшін бастапқы күйінде циклі жоқ ақырлы
автомат табылады.
Дәлелдеу. A = (К, ∑, δ, p0, F) – ерікті алынған ақырлы автомат
болсын. Автомат құрастырайық:
A1 = (K ∪{q0}, Σ, δ∪{q0a → pi p0a → pi ∈ δ}, q0, F ∪ {q0 p0 ∈
F}).
Кез – келген x = a1 a2 ... ak – L(A) тіліне жататын тізбекше
болады, сонда және тек қана сонда, егер А автоматының келесі командалар
тізбегі бар болса:
p0a1 → p1, p1a2 → p2, ..., p h-1 ah → ph; ph ∈ F
және оған сәйкес келетін А1 автоматының командасының тізбегі:
q 0a1 → p1, p1a2 → p2, ..., p k-1 ak → ph
Олай болса, A = A1 болады.
Теорема. Ерікті ақырлы автомат үшін қорытынды күйінде циклі жоқ
эквивалент автомат табылады.
Дәлелдеу: Алғашқы күйде автоматтың циклі жоқ болсын деп есептейік. A
= (К, ∑, δ, p0, F) берілген ерікті ақырлы автоматқа жаңа А1 автоматын
біріктіре қояйық:
A1 = (K∪{f}, Σ, δ∪{qja → f pja → pi∈δ & pi∈F}, p0, {f}∪{p0 p0 ∈
F}).
Нәтижесінде мынаны аламыз: A = A1.
Теорема. Реттелетін тілдердің жиыны иерация, жинақты итерация,
біріктіру, көбейту, қиылысу, қосымша және айырым операцияларына қатысты
тұйық болады.
Дәлелдеу. Дәлелдеу үшін сәйкес келетін ақырлы автоматтарға осы
операцияларды орындау қажет және осындай түрлендірулердің нәтижесінде
құрастырылған автомат талап етілген тілді қабылдайтынын көрсету керек.
Автоматта бастапқы және соңғы күйлердегі циклдер жойылған деп
жорамалдаймыз. Теоремада көрсетілген операцияларды орындау үшін берілген
автоматтарға сәйкес түлендірулерді орындау қажет.
1) Итерация операциясы бастапқы және соңғы күйден циклдерді жойып
және алынған күйлерді біріктірудің негізінде жүзеге асырылады. Бастапқы
және соңғы күйлерді біріктіру, құрастырылған автоматтың бос тізбекшені
қабылдайтынын білдіреді.
Ағымды автоматтың бастапқы күйінен соңғы күйіне бір рет өту L
тілінің тізбекшесінің қабылдануына сәйкес келеді. Күйлер
біріктірілгендіктен, автомат LL, LLL және т.б. тізбекшелерді де
қабылдайды, яғни ол {ε}∪L∪L2∪ . . . =L* тілін таниды.
2) L(A1) және L(A2) - ге көбейту операциясын қолдану екі
түрлендірудің көмегімен жүргізіледі: а) A2 – нің бастапқы күйінен және A1 -
дің соңғы күйінен циклдер жойылады; б) A1 – дің әрбір қорытынды күйіне
сәйкес өзінің данасы A2 – ні қоямыз және A1 – дің қорытынды күйіне сәйкес
келетін данасы А2 - нің бастапқы күйін біріктіреміз.
3) L(A1) және L(A2) - ні біріктіру A1 және A2 – нің бастапқы
күйлеріндегі циклді жойып және алынған бастапқы күйлерді біріктірудің
көмегімен алынады.
4) Жинақты итерация екі түрлі әдіспен құрастырылады:
а) L(A1)+ = L(A1)* L(A1),
б) L(A1) + = L(A1) L(A1)*.
5) Σ* дейінгі L(A1) қосымшасын қарастырайық. A1 автоматы
детерминерленген болсын, онда x=a1a2 . . an кез – келген тізбекшесі жалғыз
ғана жолмен танылады:
p0a1 → p1
p1a2 → p2
. . .
pn-1an → pn, pn∈ F.
Автомат тек мына тізбекшелерді ғана танымайды:
1) автомат не оны оқығанда қорытынды емес күйге өтетін a1a2 . . aj
тізбекшесінің алғашқы бөлігін береді;
2) не y = a1a2 . . . akbc1c2 . . cm (k n) немесе y = a1a2 . . .
akbc1c2 . . cm (k n) түрінде болады, мұндағы a1a2 . . ak тізбекшенің
басы x∈L(A1) тізбекшесінің басына сәйкес келеді, бірақ ak символынан кейін
A1 автоматы оны оқи алмайтын b символы тұрады.
Сондықтан тілдің қосымшасын танитын автомат құрастыру үшін қажет:
а) барлық қорытынды күйлерден қорытынды емес, ал қорытынды емес
күйлерден қорытынды күйлер жасау керек;
б) қосымша күй енгізіп, одан қорытынды күй жасау керек және әрбір
күйден осы күйде оқылмайтын, алфавиттің символына сай келетін доғалардың
күйін келтіру керек;
в) құрастырылған қосымша күйлерде c1c2 . . cm тізбекшесінің ерікті
аяқталуын оқуды қамтамасыз ету үшін, алфавиттің барлық символына тармақ
құру керек.
6) L(A1) және L(A2) айырымы келесі түрлендіруге сәйкес құрылады:
L(A1) \ L(A2) = L(A1) ∩ L(A2) .
7) Қиылысу операциясы келесі түрлендіруге сәйкес құрылады:

L(A1) ∩ L(A2) = L(A1) ∪ L(A2) .
Осы теореманың негізінде ақырлы автоматтарды құрастыруға болады.

4. Автоматты грамматикалар

Сызықты грамматикалар (оң рекурсивті және сол рекурсивті) автоматты
грамматикалар деп аталады, өйткені оларда туындаған тілдер ақырлы
автоматтармен танылатын тілдерге сәйкес келеді.
Теоремалардың қатарын қарастырайық.
Теорема. Әрбір оң сызықты грамматикаларға эквивалентті ақырлы автомат
сәйкес келеді.
Дәлелдеу. Ерікті оң сызықты G грамматикасының әрбір терминалына
сәйкес ақырлы А автоматының бір күйін қояйық. Тағы да бір күй – жалғыз
ақырлы күйді қосайық. Аксиомаға сәйкес келетін күйді алғашқы күй деп
атаймыз.
A→aB әрбір ережеге сәйкес Aa → B командасын қояйық, ал әрбір
терминальды ережеге A → a сәйкес Aa → F командасын қояйық.
Осылайша грамматикадағы тізбекшені шығарып аламыз:
S ⇒ a1A1 ⇒ a1a2A2 ⇒ ... ⇒ a1a2...a k-1A k-1⇒ a1a2 ...akk А
құрастырылған автоматының командалар тізбегі бір – біріне бірмәнді сәйкес
келеді:
Aa1 → A1; A1a2 → A2; . . . ; Ak-1ak → F. Осылайша, L(G) = L(A)
тілдері тең болады.
Мысал. G берілген грамматика үшін ақырлы автомат құрастыру қажет
болсын.
S → aS bB;
A → aA bS;
B → bB с cA.
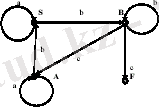Шешімі. Граф автоматы төрт төбеден тұрады, оның үшеуі S, A, B
грамматикасының терминалданбаған символдарымен белгіленбеген, ал төртінші
төбе F символымен белгіленген, ол жалғыз қорытынды күй болып табылады.
Бастапқы күй болып S аксиомасына сай келетін төбе табылады (сурет 1).

Сурет 1 Төрт төбеден тұратын автомат графы

Грамматиканың әрбір ережесіне ақырлы автоматтың командасын сәйкес
қояйық:
Sa → S – бастапқы күйде кіріске а терминальды символы түскенде
автомат сол S күйінде қалады;
Sb → B – бастапқы күйде кіріске b терминалы түскенде автомат В күйіне
өтеді;
Bb → B – В күйінде кіріске b терминалы түскенде автомат сол В
күйінде қалады;
Bc → F – В күйінде кіріске c символы түскенде автомат F қорытынды
күйіне өтеді;
Bc → A - В күйінде кіріске c символы түскенде автомат А күйіне
өтеді;
Aa → A – А күйінде кіріске а терминалы түскенде автомат сол А күйінде
қала береді;
Ab → S - А күйінде кіріске b терминалы түскенде автомат S күйіне
өтеді.
Алынған детерминерленбеген ақырлы автомат G оң рекурсивті
грамматикасынан туындаған тілдердің тізбекшесін таниды.
Теорема. Ерікті ақырлы автомат үшін эквивалентті оң сызықты
грамматика табылады.
Дәлелдеу. Ерікті автоматтың әрбір күйіне сәйкес грамматиканың
терминал емесі қойылған және бастапқы күйге аксиома сәйкес келеді.
Онда грамматиканың ережелерінің жиынының Ac → B әрбір командасына A →
cB ережесін қосып жазайық, егерде B – қорытынды күй болса, онда A → c
ережесін қосамыз.
Ағымды ақырлы автомат пен құрастырылған грамматиканың
эквиваленттілігі айқын көрініп тұр.
Теорема. Әрбір сол рекурсивті грамматика үшін эквивалентті ақырлы
автомат табылады.
Дәлелдеу. Ерікті сол рекурсивті грамматиканың әрбір терминальды емес
символы үшін ақырлы автоматтың күйін сәйкес қояйық, сонымен қатар S
аксиомасына сәйкес келетін күйді қорытынды күйетіп тағайындаймыз. Тағы бір
N күйін қосамыз және оны бастапқы күй қыламыз.
Грамматиканың әрбір A → Ba ережесіне сәйкес Вa → A автоматының
командасын қоямыз. Сонда грамматикадағы әрбір шығысқа:
S⇒A1a.k⇒A2ak-1ak⇒ ... ⇒Ak-1a2a3...ak ⇒ a1a2 . . . ak құрастырылған А
автоматының командалар тізбегі бірмәнді сәйкес келеді:
Na1 → Ak-1; . . .; A2ak-1 → A1; A1ak → S.
Осылайша L(G) = L(A) тілдері тең болады.
Теорема. Ерікті ақырлы автомат үшін эквивалентті сол рекурсивті
грамматика табылады.
Дәлелдеу. Ерікті автоматтың әрбір күйіне грамматиканың терминальды
емес символын қоямыз, S терминал емесін қоямыз және оны аксиома етіп
тағайындаймыз.
Ережелер жиынындағы әрбір Aa → B командасына сәйкес B → Aa ережесін
қосмыз, бұл жағдайда егер В – қорытынды күй болса, онда қосымша S → Aa
ережесін енгіземіз, ал егер A – бастапқы күй болса, онда қосымша B → a
ережесін енгіземіз.
Онда командалардың тізбегіне:
A0a1 → A1; A1a2 → A2; . . . ; Ak-1ak → F
келесі қорытынды сәкес келеді:
S ⇒ A k-1ak ⇒ ... ⇒ A1a2a3...ak ⇒ a1a2a3...ak.
Автоматты грамматикалардың маңызды ерекшеліктері болып оларды ақырлы
графтардың көмегімен көрсету мүмкіндігі саналады. Графтың грамматикасы
бойынша керекті тізбекшенің қорытындысы жеңіл тауып алынады.
Автоматты грамматикада тізбекшенің кез – келген қорытындысы осы
грамматиканың графтағы жолына сәйкес келеді, S төбесінен (аксиомамен
белгіленген төбе) басталады және ақырлы төбеде аяқталады.
Мысал. L(A) = {(ab)*} тілін танитын ақырлы автомат ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.