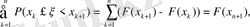Үлестірім функциясы сол жағынан үздіксіз функция

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Үлестірім функциясы

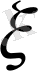кездейсоқ шамасының ықтималдықтар үлестірімінің заңдылықтарын басқа да әдіспен сипаттауға болады. Ол үшін 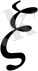-дің мәндері тиянақты бір х саныан кіші болу ықтималдығы қарастырылады.

Дискретті 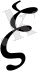кездейсоқ шамасы үшін:

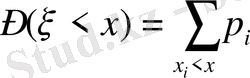, (6)

Мұндағы х ₁ , х ₂ . . . , х _n - кездейсоқ шаманың қабылдайтын мәндері, р ₁ , р ₂ , . . . р _n - сол мәндерді қабылдау ықтималдықтары, ал қосынды теңсіздігіне сәйкес барлық р _і сандары бойынша алынады.

Ықтималдық үлестірім тығыздығы 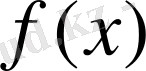функциясы болатын үзіліссіз кездейсоқ 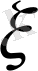шамасы үшін

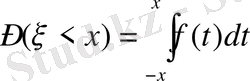(7)

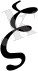функциясын кездейсоқ шамасының үлестірім функциясы деп атайды да, оны 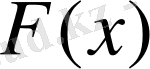арқылы белгілейді:

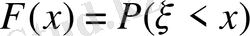Сонымен, үлестірім функциясы дискретті, сондай - ақ үзіліссіз кездейсоқ шамаларға қатысты. Сондықтан да ол кездейсоқ шаманың жалпы сипаттамасы болады.

Мысалдар.

1. 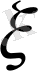кездейсоқ шамасының үлестірім таблицасы мынадай болсын:

: р

0: 0, 2

1: 0, 5

2: 0, 2

3: 0, 1

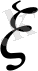
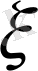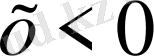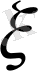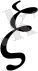үлестірім функциясын табалық. Ол үшін (6) теңдікті қолданамыз. Егер болса, онда -дің қабылдайтын мәні жоқ; болғанда -дің қабылдайтын мәні 0; 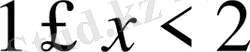болғанда 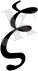-дің қабылдайтын мәндері 0 мен 1; егер болса, онда 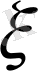-дің қабылдайтын мәндері 0, 1 мен 2; ақырында, 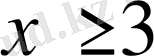болғанда, 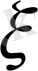кездейсоқ шамасы өзінің мәндерінің бәрін қабылдайды. Міне, осы айтылғандарды біріктіріп жазсақ, (6) теңдік негізінде үлестірім функциясы мынадай болады.

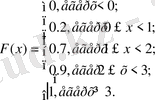
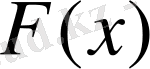функциясының графигі суретте келтірілген.

2. (а, b) аралығынан мән қабылдайтын бірқалыпты үлестірім функциясын табу керек.

Шешуі. алдыңғы тақырыпта бірқалыпты үлестірім тығыздығын

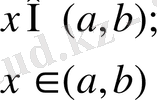егер

егер

теңдігі арқылы анықтағанбыз. Осыған сәйкес (7) теңдікті қолданып және тиесілі интегралды есептеп, бірқалыпты үлестірім функциясын табамыз (2-сурет. ) :

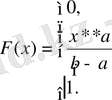егер

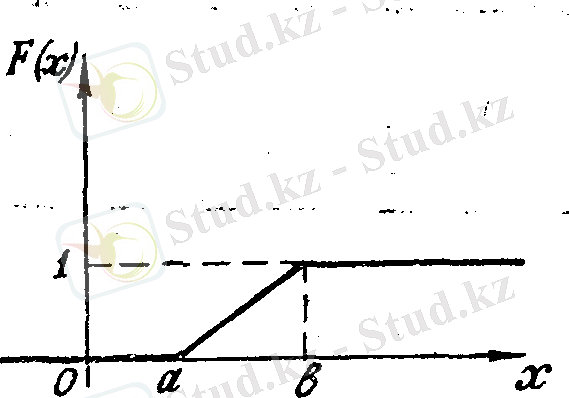
2 - сурет 3 - сурет

Алдыңғы тақырыпта берілген N(а, b) қалыпты үлестірім тығыздығы бойынша қалыпты үлестірім функциясы былай анықталады:

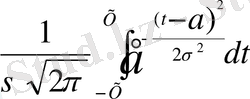
Ф(х) =

мұндары а, >0-нақты параметрлер.

ξ кездейсоқ шамасының үлестірім функциясы F(х) белгілі болса, онда сол кездейсоқ шаманың мәндері кез келген [а, 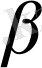] aралығында жату ықтималдығын тауып алуға болады, атап айтқанда, мынандай теңдік орынды:

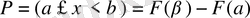
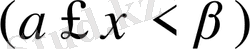
Шынында да, ( 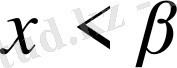) оқиғасын (ξ<а) және оқиғаларының қосындысы деп қарастыруға болады, сондықтан ықтималдықтарды қосу теоремасы бойынша 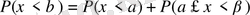(8) теңдік бойынша 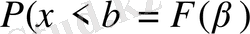және Р= (ξ <а) = F (а) болатындығын ескерсек, соңғы теңдіктен дәлелдегелі отырған (9) теңдік келіп шығады.

Үлестірім функциясының қасиеттерін келтірейік:

Үлестірім функциясы шектелген, яғни. Бұлай болатын себебі - анықтама бойыншафункциясы (8) теңдік негізінде ықтималдықты көрсетеді, ал ықтималдық 0 мен 1-дің арасынедағы сан.
және. Үлестірім функциясының бұл қасиеті (6) және (7) теңдіктерден тікелей келіп шығады.
Үлестірім функциясы кемімейтін функция, яғниболғанда, болады. Шынында да, (9) теңдікті [) аралығына қолдансақ,, алдемек, .
Үлестірім функциясы сол жағынан үздіксіз функция

Дәлелдеу:

Кез келен а нүтесін алалық. Бұл нүктеге сол жағынан жинақты өспелі { x _n } тізбегін әр уақытта тауып алуға болады. { x _n } тізбегінің мүшелеріне сәйкес оқиғалар құрсақ,

(10) .

Ықтималдықтар теориясының аксиомалары бойынша

(11) .

(11) теңдіктегі шектің астында тұрған ықтималдықтарға (9) теңдікті қолдансақ, онда

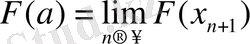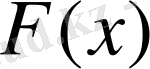ал мұны (10) теңдікпен салыстырсақ, . Бұл функциясының нүктесінде сол жағынан үзіліссіз екендігін көрсетеді.

Математикалық теория тұрғысынан қарағанда үлестірім функциясы өте күрделі болуы мүмкін. Бірақ та біз бұл функция жоғарыдағы төрт қасиетті қанағаттандыруын талап етеміз. Жаратылыстану мен техниканың реальдық есептері қарапайым функцияларға - баспалдақты (дискретті жағдайда) немесе үзіліссіз (кездейсоқ шама үзіліссіз болған жағдайда) функцияларға келтіріледі. Осыған орай, курсымыздың барысында үлестірім функциясы үзім - үзім дифференциалданатын деп, басқаша айтқанда оның үзілліссіз нүктелерінің жиыны саналатын және оның туындысы бар деп ұйғарамыз.

Үлестірім функциясын есептеуге бір мысал келтірейік:

Есеп

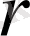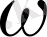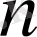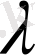Берілген 0 центрінен радиусы -ге тең сферасы жүргізілген, содан кейін облысында нүктелер қалай болса солай орналастырылған. болғанда, мұндағы пропорционалдық коэффициент, бірде - бір нүкте 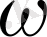сферасының ішінде жатпай ықтималдығы қандай?

Шешуі:

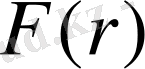арқылы центрге ең жақын нүкте қашықтғының үлестірім функциясын белгілелік, яғни 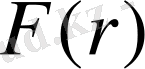- центрге ең жақын нүкте қашықтығы 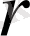-ден кіші болу ықтималдығы. Демек, 1- 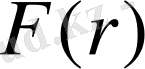ізделінді ықтималдық. Нүктелердің әрқайсысы 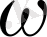сферасында 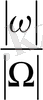ықтималдығымен жатады. Олай болса, нүктелердің 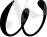сферасында бірде - бір жатпау ықтималдығы 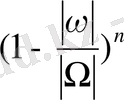. Енді шар көлемі 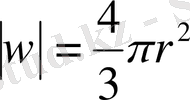болатындығын ескерсек,

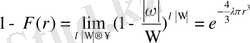, бұдан

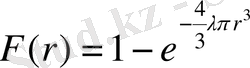Бұл табылған үлестірім функциясын астрономияда қолдануға болады. Егер «нүкте» дегеннің орнына «жұлдыз» деп алсақ, онда 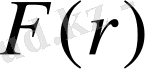функциясын кез келген жұлдыздан оған ең жақын жатқан жұлдыздың қашықтығының ықтималдық үлестірім заңы болады, демек, оны жұлдыздар статистикасына қолдануға болады. Мысалы, Күннің төңірегінде 1 парсек ³ шамасында жатқан жұлдыздардың орта санын 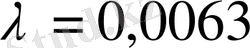деп алуға болады екен.