Түзудің нормаль теңдеуі, нүктеден түзеге және жазықтыққа дейінгі қашықтық формулалары және кеңістіктегі түзулердің теңдеулері


 Егер кординаталар басынан түзуге түсірілген перпендикулярдың ұзындығын
Егер кординаталар басынан түзуге түсірілген перпендикулярдың ұзындығын
 -ге тең, ал оның абсциссалар осінің оң бағытымен жасайтын бұрышы
-ге тең, ал оның абсциссалар осінің оң бағытымен жасайтын бұрышы
 -ға тең деп алсақ, берілген түзудің теңдеуін
-ға тең деп алсақ, берілген түзудің теңдеуін
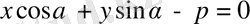
түрінде жазуға болады. Мұндай теңдеуді түзудің нормаль теңдеуі дейді. Бұл теңдеудің коэффициенттері төмендегідей екі шартқа бағынады:
1)
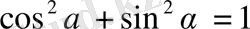
2)
Егер түзудің жалпы теңдеуі
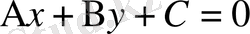 берілсе, оны
берілсе, оны
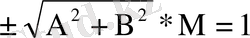 теңдігінен анықталатын М шамасына көбейтіп,
теңдігінен анықталатын М шамасына көбейтіп,
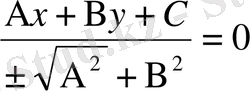
нормаль түріне келтіруге болады. Мұнда нормалаушы көбейткіш М-нің таңбасы шарт бойынша С-нің таңбасына қарама-қарсы болып алынады.
Берілген
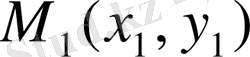 нүктесінен берілген
нүктесінен берілген
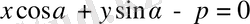 түзуіне дейінгі қашықтық
түзуіне дейінгі қашықтық
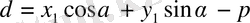
формуласымен есептелінеді. Егер түзу жалпы теңдеуімен берілсе,
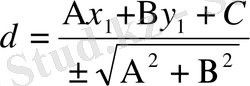
Бұл формулалармен есептегенде d оң сан да, теріс сан да болуы мүмкін. Егер берілген нүкте мен кординаталар басы берілген түзудің екі жағында жатса, онда d- оң сан, ал егер берілген нүкте мен кординатлар басы берілген түзудің бір жағында жатса, d-теріс сан болады. Егер қашықтық өзі ғана керек болса, онда
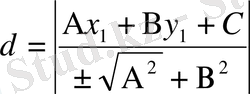
формуласын пайдаланады.
Түзуді берілген екі түзуден бірдей қашықтықта жататын нүктелердің геометриялық орны ретінде қарастыруға болады. Егер берілген екі түзу қиылысатын болса онда бұл геометриялық орын екі түзудің қиылысу бұрыштарының биссектрисаларын анықтайды. Мұнда бір биссектриса үшін
 болса, екінші биссектриса үшін
болса, екінші биссектриса үшін
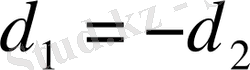 . Бұл жерде d әріпінің таңбалары ескеріледі. Егер берілген екі түзу параллель болса, онда бұл геометриялық орын берілген түзулерге параллель болып, олардың дәл аралығынан өтеді. Бұл жағдайда да таңба ескеріледі. Мысал үшін
. Бұл жерде d әріпінің таңбалары ескеріледі. Егер берілген екі түзу параллель болса, онда бұл геометриялық орын берілген түзулерге параллель болып, олардың дәл аралығынан өтеді. Бұл жағдайда да таңба ескеріледі. Мысал үшін
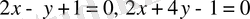 түзулерінің бірдей қашықтықта жататын нүктелердің геометриялық орнын табайық. Берілген түзулер параллель болмайды, сондықтан мұндай геометриялық орын биссектрисаларды анықтайды. Егер геометриялық орын биссектисаларды анықтайды. Егер геометриялық орынды анықтайтын түзудегі кез келген нүктені
түзулерінің бірдей қашықтықта жататын нүктелердің геометриялық орнын табайық. Берілген түзулер параллель болмайды, сондықтан мұндай геометриялық орын биссектрисаларды анықтайды. Егер геометриялық орын биссектисаларды анықтайды. Егер геометриялық орынды анықтайтын түзудегі кез келген нүктені
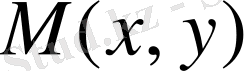 деп белгілесек,
деп белгілесек,
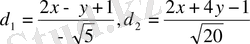
болады. Бір биссектриса үшін мына
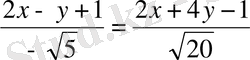
теңдігі, ал екіншісі үшін
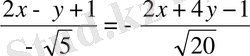 теңдігі орындалады.
теңдігі орындалады.
Түзуді берілген екі түзуден бірдей қашықтықта жататын нүктелердің геометриялық орны ретінде қарастыруға болады. Егер берілген екі түзу қиылысатын болса, онда бұл геометриялық орын екі түзудің қиылысу бұрыштарының биссектрисаларын анықтайды. Мұнда бір биссектриса үшін d
1
-d
2
болса, екінші биссектриса үшін
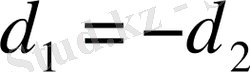 . Бұл жерде
. Бұл жерде
 әріпінің таңбалары ескеріледі. Егер берілген екі түзу паралель болып, олардың дәл аралығынан өтеді. Бұл жағдайда да таңба ескеріледі. Мысал үшін
әріпінің таңбалары ескеріледі. Егер берілген екі түзу паралель болып, олардың дәл аралығынан өтеді. Бұл жағдайда да таңба ескеріледі. Мысал үшін
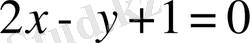 және
және
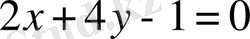 түзулерінен бірдей қашықтықта жататын нүктелердің геометриялық орнын табайық. Берілген түзулер параллель болмайды, сондықтан мұндай геометриялық орын биссектрисаларды анықтайды. Егер геометриялық орынды анықтайтын түзудегі кез келген нүктені
түзулерінен бірдей қашықтықта жататын нүктелердің геометриялық орнын табайық. Берілген түзулер параллель болмайды, сондықтан мұндай геометриялық орын биссектрисаларды анықтайды. Егер геометриялық орынды анықтайтын түзудегі кез келген нүктені
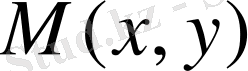 деп белгілесек,
деп белгілесек,
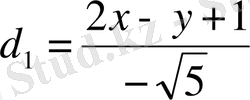 ,
,
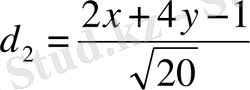
болады. Бір биссектриса үшін мына
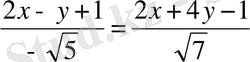
теңдігі, ал екіншісі үшін
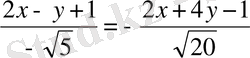
теңдігі орындалады. Онда биссектрисалардың
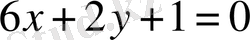 ,
,
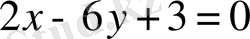 теңдеулері шығады. Биссектрисалардың біріне-бірі перпендикуляр екендігі көрініп тұр.
теңдеулері шығады. Биссектрисалардың біріне-бірі перпендикуляр екендігі көрініп тұр.
Егер
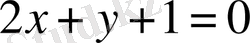 ,
,
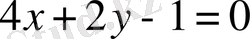 параллель түзулері берілсе, онда екеуіне де бірдей қашықтықта жататын нүктелердің геометриялық орны сол түзулердің арасында жататын, екеуіне де параллель түзуді
параллель түзулері берілсе, онда екеуіне де бірдей қашықтықта жататын нүктелердің геометриялық орны сол түзулердің арасында жататын, екеуіне де параллель түзуді
анықтайды. Бұл берілген түзулер кординаталар басының екі жағында жатады. Сондықтан
 деп аламыз:
деп аламыз:
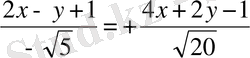
Осыдан ізденіліп отырған түзудің
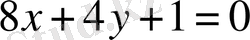 теңдеуі табылады.
теңдеуі табылады.
Кеңістіктегі түзудің теңдеулерін мынадай төрт түрін жазуға болады.
1. A 1 x+B 1 y+C 1 z+D 1 =0
A 2 x+B 2 y+C 2 z+D 2 =0
2.
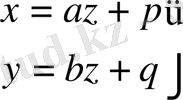
3.
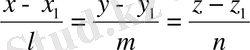
4.
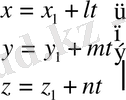
Жазықтықтың
 нормальдық теңдеуі және кеңістіктегі
нормальдық теңдеуі және кеңістіктегі
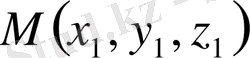 нүктесі берілген. Осы нүктеден берілген жазықтыққа дейінгі қашықтықтың формуласын қорытып шығарайық. Берілген жазықтықты P деп белгілейік. Кеңістіктегі M нүктесінен берілген P жазықтыққа паралелль көмекші Qжазықтығын жүргізейік. Іздеп отырған қашықтық осы екі жазықтыққа перпендикуляр, яғни
нүктесі берілген. Осы нүктеден берілген жазықтыққа дейінгі қашықтықтың формуласын қорытып шығарайық. Берілген жазықтықты P деп белгілейік. Кеңістіктегі M нүктесінен берілген P жазықтыққа паралелль көмекші Qжазықтығын жүргізейік. Іздеп отырған қашықтық осы екі жазықтыққа перпендикуляр, яғни
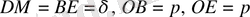 осыдан
осыдан
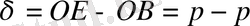
Qжазықтығының теңдеуін Mнүктесінің координаталары қанағаттандырады.
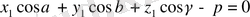 Осыдан
Осыдан
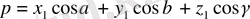 . Енді p-тің мәнін мына
. Енді p-тің мәнін мына
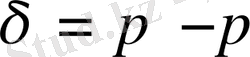 теңдігіне қойып, іздеген формуланы табайық:
теңдігіне қойып, іздеген формуланы табайық:
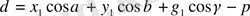
Егер Mнүктесі берілген Pжазықтығы мен кординаталардың бас нүктесінің арасында жатса онда
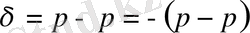 қашықтығының таңбасы теріс болады. Сондықтан берілген жазықтыққа дейінгі қашықтықтың формуласы мынадай болады:
қашықтығының таңбасы теріс болады. Сондықтан берілген жазықтыққа дейінгі қашықтықтың формуласы мынадай болады:
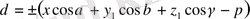 .
.
Бұл теңдеуден мынадай ереже шығады, берілген нүктеден берілген жазықтыққа дейінгі қашықтықты табу үшін сол берілген нүктенің координаталарын берілген жазықтықтың теңдеуіндегі ағымдық координаталардың орнына қою керек.
Егер жазықтық жалпы түрде берілсе, онда оны нормальдық түрге келтіріп, ондағы ағымдық координаталардың орнына берілген нүктенің координаталарын қоямыз.
 .
.
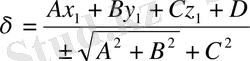
Түзудің теңдеуін сызу үшін теңдеуді екі жазықтықтың қиылысқан сызығы деп қарастырмай -ақ арнаулы бір қасиеті бар нүктелердің геометриялық орны деп қарастыруға болады. Кеңістіктегі түзудің орнын анықтау үшін, түзу бойындағы бір нүкте көрсетіліп түхудің бағыты белгіленген болса болғаны. Белгілі нүктесі арқылы өтетін түзуді делік. Бұл түзудің бағыты координат сабақтарымен жасайтын бұрыштары арқылы көрсетілген болсын. Түзудің теңдеуін құру үшін, түзу бойынан кез келген бір нүкте алайық: M(x y z) MM кесіндісінің OX сабағындағы проекциясын былай жазуға болады:
M 1 M= A 1 A 2 =x-x 1
Вектордың ұзындығы мен проекциясының арасындағы байланыс былай болады:
Cos a=x-x
1
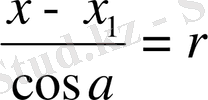
1. Түзудің теңдеулері жалпы түрде берілген:
2х+3у-12z-5=0
x-6y+4z+5=0
Осы түзудің теңдеуін басқа түрде жазып көрсетініз.
Шешуі: 1. Бұл теңдеулерді х пен у ке арнап шешсек, сонда түзудің екінші теңдеулері шығады:
2х+3y-12z-5=0 /2 4x+6y-24z-10=0
x-6y+4z+5=0 +
x-6y+4z+5=0
5x-20z-5=0
Ықшамдап 5-ке қысқартқаннан кейін х=4z+1 болады.
2х+3y-12z-5=0 /2 2x+3y-12z-5=0
x-6y+4z+5=0 +
-2x+12y-8z-10=0
15y-20z-15=0
Ықшамдағаннан кейін,
Y=4/3z+1 болады
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz