Толқындық оптика негіздері: когеренттік, суперпозиция және интерференция


Тақырыбы: Толқындық оптиканың негіздері.
Лекция жоспары:
1. Тербелістер мен толқындардың негіздері.
2. Когоренттік толқындарды алу жолдары.
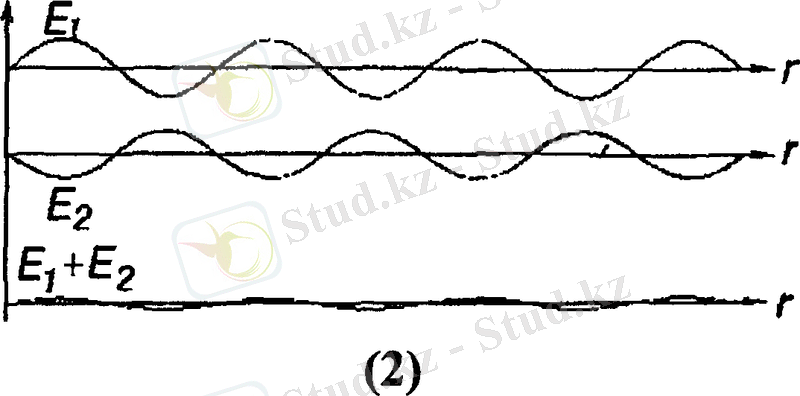
1. Когеренттілік - деп бірнеше тербелістердің немесе толқындық процестердің үйлесімді өтуін айтады. Дәлме - дәл когеренттік болуы тек когеренттік толқындардың үлесіне ғана тиеді.
Монохроматтық (грек сөзі монос-бір және хрома - түс) толқындардың амплитудасы, жиілігі және бастапқы фазалары ұзақ уақыт бойы өзгеріссіз сақталады. Сондықтан да жиілігі бірдей екі монохроматтық толқындардың әрбір нүктедегі фазалар айырымы тұрақты болып қалады. Қарастырылып отырған мәселені тереңірек түсіну үшін, әуелі мына төмендегі жағдайларға көңіл аударайық.
Когоренттік жарық толқындарын алу үшін практикада бір жарық көзінен шығатын толқынды екі бөлікке (шағылдыру, не сындыру арқылы) жіктейді. Сонан соң осы толқындарды бріне-бірін беттестіргенде, яғниоларды бір-біріне қосқанда интерференция құбылысы байқалады.
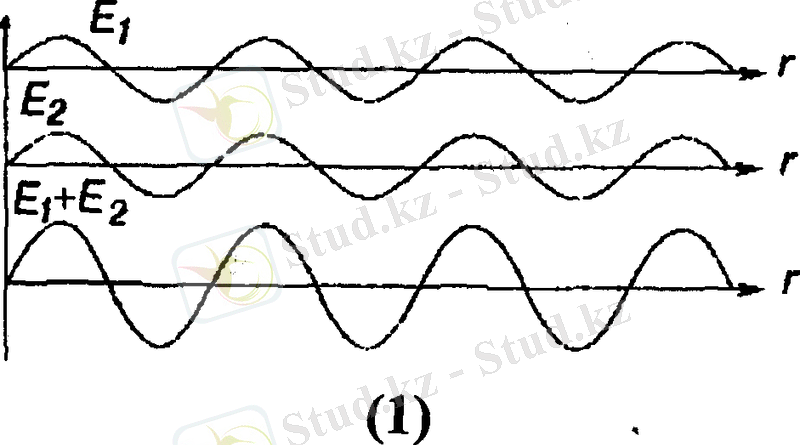
Әдетте бір уақыт аралығында кеңістікте әр түрлі жарық көздерінен көптеген жарық толқындары таралып жатады. Тәжірибе көрсеткендей бұл толқындардың таралуы бір - бірінен тәуелсіз және олар бір - бірімен қосылғанда нәрсенің кескіні еш бұрмаланбайды. Бұндай жағдайды суперпозиция принципі деп атайды. Егер кеңістікте бірнеше электромагниттік толқындар болса және олар үшін суперпозиция принципі сақталса, онда кейбір толқындардың магнит және электр өрістерінің кернеуліктері алгебралық түрде қосылады. Сондықтан суперпозиция принципін математика жолымен былай өрнектейді.
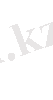
Мұндағы
Суперпозиция принципі тек әлсіз өрістер үшін ғана орындалады. Күшті жарық өрісінде суперпозиция принципі орындалмайды, яғни сызықтық принциптер пайда болады. Оптиканың бұл саласын сызықтық оптика дейді.
Жарық толқындары әсерлескенде, әсіресе, бірдей жиілікті екі толқынның қосылуы кезіндегі процесс аса көңіл бөлерлік жағдай. Мұндайда интерференция құбылысы байқалады, яғни екі толқын кеңістіктің бір нүктесінде бірін - бірі күшейтеді, не өшіреді.
 Енді толқындадрды қосуды математика
Енді толқындадрды қосуды математика
Тұрғысынан қарастырайық. Ол үшін ең
қарапайым жиілігі бірдей сызықша
поляризацияланған екі монохроматтық
толқынды алайық, олардың тербеліс
бағыттары да бірдей болсын. Математикалық
өрнектеуге жеңілдік келтіру үшін толқын амплитудалары бірдей деп қарастырамыз, сонда
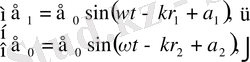
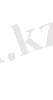 (2)
(2)
мұндағы r 1 мен r 2 - жарық көздері I 1 мен I 2 - ден бақыланып отырған нүктеге дейінгі қашықтықтар;
Суперпозиция принципі бойынша
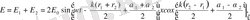 (3)
(3)
мұндағы r 2 - r 1 - ді интерференцияланатын сәулелердің жол айырымы дейді.
(3) өрнектегі бірінші көбейткіш
Е - нің уақытқа тәуелділігін
сипаттайды. Ол қорытқы өрістің
қосылатын өрістер жиілігіндей
жиілік пен тербелетіндігін көрсетеді
және фазалары жағынан да айырмасы
шамалары. Екінші көбейткіш уақыттан тәуелсіз, оны Е 0 деп белгілейік, сонда
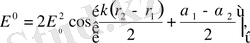 (4)
(4)
Демек, қаралатын нүктедегі қорытқы амплитуданы табуға болады. Ол үшін жоғарыдағы (3) өрнегіне оралайық. Онда біз мынаны жазғанбыз:
Осыдан шығатыны
Пойнтинг векторының модулінің орташа мәні Е о Н о -ге пропорционал. Сондықтан
мұндағы А-толқынның амплитудасы. Жарық таралатын ортаның сыну көрсеткіші біз қарастырып отырған жағдай үшін n=1, сондықтан
І~А 2 (6)
Егер біз (5) өрнегін пайдаланып және Пойнтинг векторының
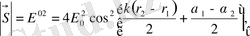 (7)
(7)
(7) теңдеудегі
мұндағы
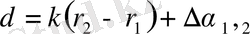 (9)
(9)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz