Тербелістер және тербелмелі жүйелер: түрлері, энергиясы және динамикасы


Мазмұны.
Кіріспе.
I . Тарау. Тербеліс және олардың түрлері.
§. 1. 1. Тербеліс туралы жалпы түсінік.
§. 1. 2. Өшетін тербелістер.
§. 1. 3. Мәжбүр тербелістер.
§. 1. 4. Гармониялық тербелістер.
- Тарау. Тербелмелі жүйе . Тербеліс қозғалысының энергиясы, жылдамлығы, үдеуі.
§. 2. 1. Тербелмелі жүйе.
§2. 2. Тербелмелі қозғалыс энергиясы.
§2. 3. Гармониялық тербелмелі қозғалыстың жылдамдығы, үдеуі және энергиясы.
§2. 4. Эксперименттік бөлім.
Қорытынды.
Пайдаланылған әдебиеттер.
I . Тарау. Тербеліс және олардың түрлері.
§. 1. 1. Тербеліс туралы жалпы түсінік
Тербеліс деген өте кең ұғым. Айталық маятник тербелісі, машиналар двигателі поршенінің қозғаласы, кеменің шайқалысы, көпір мен үйлердің теңселісі, айнымалы токтың тізбектегі тербелісі, жүрек соғысы және «Тербелер дауысым ауада . . . » -деп Сәкен Сейфуллин айтқан ауаның тербелісі, міне осының бәрі тербелістің мысалдары бола алады. Сонымен тербеліс деп белгілі уақыт өткенде қайталанып отыратын процестерді, қозғалыстарды айтады. Тербелмелі қозғалысты (тербелісті ) қарастырғанда, тербелістің қайталануын сипаттайтын белгілерді ажыратып алғын жөн.
Олар мыналар:
- Бастапқы қалпына қайтып келгенде дейінгі кететін уақыт.
- Тепе- теңдік күйден шыққаннан кейінгі ең үлкен ауытқу .
- Тербелісті сипаттайтын заңдылықтың математикалық түрі.
Тербеліп тұрған жүйені тербеліс жүйесі деп атайды . Егер тербелмелі жүйенің энергиясы өзгермесе, онда оны өшпейтін тербеліс, ал энергиясы азая беретін болса онда оны өшетін тербеліс деп атайды. Тербеліс кезінде өзгеретін физикалық шамалардың мәні бірдей уақыт ішінде қайталанып отыратын болса, онда тербелісті периодты тербеліс деп атайды. Тербелмелі қозғалыстағы дененің бұрынғы қалпына қайтып келуіне кеткен ең аз уақытты период (Т ) деп атайды. Бұл уақыт ішінде бір толық тербеліс жасалады . Уақыт бірлігі ішінде жасалатын толық тербелістер санын периодты тербелістердің жиілігі деп атайды:
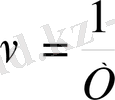
Бір секундта бір тербеліс жасайтын тербеліс жиілігініің бірлігі Герц (Гц) деп аталады. Ал 2π секунд ішінде жасалатын тербелістер санын периодты тербелістердің циклдік (дөңгелектік ) жиілігі (ω) деп атайды :
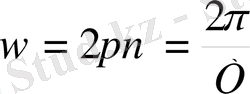
Осыдан :
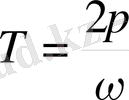 (1)
(1)
Тербеліс күрделі немесе қарапайым болуы мүмкін . Синус (косинус) заңына бағынатын тербелістерді қарапайым тербелістер атайды. Оған гормлниялық тербелістер жатады. Механикалық тербелістердің заңдылықтарын зерттеуді гормониялық тербелістерден бастаймыз.
Шеңбер бойымен қозғалған материалдық нүктені алайық. Нүктінің N 0 -ден шығып, шеңбер бойымен сағат тілі бағытында қозғала отырып, қайтадан N 0 - ге қайтып келуге кеткен уақытын тербеліс периоды деп атайды. Ол Т әрпімен белгіленеді. Материалдық нүктенің тепе - күйден ауытқуын ығысу деп атайды.
КN 1 =x;
Ең үлкен ығысу амплитуда деп аталады. Оны А әрпімен белгілейді:
ON 2 =A;
Тербеліп тұрған нүктенің әрбір уақат кезеңіндегі жағдайы фазамен сипатталады. Тербелмелі қозғалыстағы нүкте қозғалысының негізгі теңдеуін табу үшін KON 1 үшбұрышын қарастырайық . Одан :
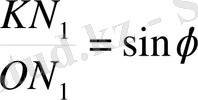
Немесе
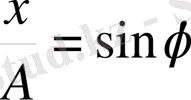
Бұдан : x= A sin φ (2)
Осы теңдеу гармониялық тербелістің теңдеуі болып саналады. Біз бұл жерде t=0 болғанда дене тыныштық күйде тұр деп алып отырмыз.
Нүкте Т секунд ішінде бір айналым жасайды, яғни 2π доғасын жүріп өтеді t уақыт ішінде φ жағдайында болсын делік. Осы төрт шаманың арасында мынадай тәуелділік бар:
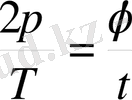 , осыдан
, осыдан
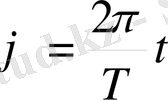 (3)
(3)
Фазаның осы мәнін (2) формулаға қойсақ, шығатыны :
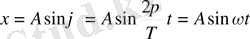 (4)
(4)
Тербеліс фазасы кез - уақыттағы ығысуды анықтайды .
Мысалы: φ = 0 0 болса, онда x=0 ; φ =30 0 болса, онда
x= A sin 90 0 = А
Тепе теңдік қалпынан шығарылған, бірақ сыртқы күштің әсерінсіз тербеліс жасап тұрған жүйенің тербелісін еркін тербеліс (меншікті тербеліс) деп атайды. Сыртқы күштің әсерінен болатын тербелісті еріксіз тербеліс деп атайды.
Серппеге қосылған магниттің тербелісі серппеге ілінген жүктің тербелісі, шекті тепе - теңдік күйінен шығарған тербелістер еркін тербелістердің мысалы бола алады.
Тербелістердің асциллограммасы .
Егер маятникке сия құйсақ маятник тербелгенде одан аққан сия маятниктің ілу нүктесіне қатысты алғанда бірқалыпты қозғалып, қағазға қисық сызады . Қағаз жолақ бір қалыпты қозғалғандықтан, алынған қисық уақыт өткен сайын маятниктің тепе - теңдік күйіне қатысты қылпынан өзгергенін көрсетеді. Мұндай қисық асциллограммалар деп аталады.
«Асциллограмма» - деген сөз латынның oscilum тербеліс және гректің графио - жазамын деген сөзінен шыққан .
Жалпы тербелістер деп периодты түрде өзгеріп тұратын сыртқы күшті ңәсерінен тербелмелі жүйеде пайда болатын тербелсті айтады.
Үйдің жанынан ауыр жүк машинасы жүріп өткендк терезе әйнектерінің сылдырлауы еріксіз тербелістер болады. Ол тербелістерді жүк машинасының әсерінен ауа мен жэердің тербелістері тудырады.
Телефонмен сөйлескенде телефон мембранасы ауа қозғалысының әсерінен тербеледі, ал ауа дауыс жарғақшасының тербелісімен ауаның тербелістері еріксіз тербелістер болып саналады. Жұмыс атқарып тұрған барлық машиналар мен механизмдердің корпустары да еріксіз тербелістер шығарады. Қатты сөйлегіштің диффузоры да еріксіз тербеліс жасайды. Осы барлық келтірілген мысалдар еріксіз тербелістердің бізді қоршаған ортада жиі кездесетінін көрсетеді.
Еріксіз тербелістердің жиілігі.
Егер серппелі маятниктің сол жақтағы серппесі аз жиілікпен тартып қойсақ, онда маятниктің жүгі де аз жиілікпен тербеле бастайды. Егер мәжбүр етуші тербелістің жиілігі де арта түседі . Мәжбүр етуші тербелістердің жиілігі неғұрлым көп болса, еріксіз тербелістің жиілігі де соғұрлым көп болады. Осы және осыған басқа да мысалдар еріксіз тербелістердің жиілігі мәжбүр етуші тербелістердің жиілігіне тең екеніне көз жеткізеді.
Қажетсіз еріксіз тербелістерді өшіру.
Еріксіз тербелістер амплитудасының құрылыстардың бұзылу қаупін тудырыратын жағдайға жетуі еріксіз тербелістерді өшіру тәсілдерін іздестіруге мәжбүр етеді. Еріксіз тербелістерді іздестірудің бір тәсілі жүйенің еркін тербелісінің жиілігін өзгертуде болып отыр. Атап айтқанда, ол жиілік еріксіз тербелістің жиілігіне дәл келмеуі керек және оған еселі болмауы керек.
Мысал: жылу электр станциясы үшін жасалатын бу турбинасының жиілігі 3000 мин -1 болуы керек. Демек ротордың айналуынан пайда болатын тербелістің жиілігі мынаған тең
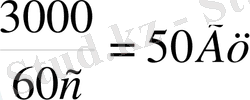
Резонанстық тербеліс болмау үшін бүкіл «Генератор - турбина - фундамент» жүйенің 50 Гц - тең өзгеше және 50 Гц - ке еселі болмайтын еріксіз тербеліс жиілігінде болу керек. Резонанспен күресудің осы әдісін тек тәжірибе жүзінде бейнелейік.
Мысалы: Вибраторды іске қосқанда серіппелі маятник үлкен амплетудамен тербеле бастайды. Бұл еріксіз тербелістердің жиілігі еркін тербелістердің жиілігіне жақын екені нақтылай түседі. Маятникті тоқтатып оның жүгін массасы артық жүкпен алмастырамыз (мұнымен біз маятник тербелісінің меншікті жиілігін өзгертеміз) . Вибраторды қайта іске қосып маятник тербелісі амплетудасымен біршама азайғанын көреміз. Енді тербеліс резонанстық сипатқа ие болмайды.
Резонанстық құбылыстармен күресудің екінші бір тәсілі жүйенің үйкелісін арттыру. Жүйенің үйкелісі неғұрлым көп болса, соғұрлым резонанстық тербелістердің амплетудасы аз болсады.
Бір түзудің бойымен болатын тербелістерді қосу.
Көбінесе дене бір мезгілде екі немесе бірнеше тербеліске қатысатын қозғалыстарда болып отырады.
Мысалы: Егер бір жүкті пружинаға асып ресорлы вагонның төбесіне іліп қоятын болсақ жүк ілу нүктесіне қатысты тербеліс жасайды, ал ол ілу нүктесінің өзі вагонның ресорларында тербеледі. Сонда жүк бір жаққа қарай бағытталған екі тербелістің қосындысы болатын қозғалыс жасайды. Осы тербелістерді қосқанда қандай қортқы қозғалыс шығатының қарастырайық. Мұны біз бір жаққа бағытталған және периодтары бірдей, бірақ фазаларында біраз айырмашылығы бар және амплитудалары әр түрлі екі тербелісті қосудан бастайды. Мынадай тербелістерді алайық:

(1)
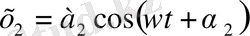
Бұл екі тербелістің периодтары тең деп алайық, сондықтан олардың дөңгелектңк жиіліктері ω бірдей болады.
Дене бір кезде екі тербеліс жасағанда, оның тепе - теңдік қалыптан ауытқуы х 1 және х 2 ауытқулардың алгебралық қосындысына тең болады:
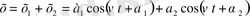 (2)
(2)
Бұл екі тербелісті х өсінде жатқан кез келген О нүктесінен бастап салынған амплитудаларының векторлары арқылы қарастырайық. Екі амплетудада бірдей бұрыштық жылдамдықпен (ω) сағат тілінің бағытына қарама - қарсы бағытпен айналады. Демек а 2 мен а 1 векторлардың арасындағы бұрыш әрқашан ά 2 - ά 1 тең болады. Екі вектордың бір өске түсірілген позицияларының қосындысының сол өске түсірілген проекциясына тең болғандықтан, қорытқы тербеліс амплитуданың векторымен кескінделеді, ол ά 2 және ά 1 амплитуда векторларын геометриялық жолмен қосқаннан шығады, яғни а = а 1 +а 2
Қортқы а амплидудасының векторы қосылатын тербелістер амплитулдалар векторларының бұрыштық жылдамдығымен айналады. Қортқы амплитуда векторының х өсімен бастапқы кезде жасайтын ά бұрышы мынаған тең болатындығын көруге болады.
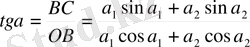 (5)
(5)
Қорытқы тербелістердің өзі а амплитудасы векторының х өсіне түсірілген проекциясының өрнектеледі, яғни ол мынаған тең болады:
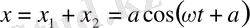 (6)
(6)
Сүйтіп қортқы қозғалыс құраушы қозғалыстар қандай түзудің бойымен болатын болса, сол түзудің бойымен болатын гармониялық тербеліс екенін және оның периоды да сол құраушы қозғалыстардың периодына тең болатынын көреміз. Қортқы тербелістің а амплитудасымен а бастапқы фазасы құраушы тербелістердің амплитудаларымен бастапқы фазалары арқылы (4) (5) формулалары бойынша анықталады. (4) формула бойынша қортқы тербелістің а амплитудасы құраушы тербелістердің а 2 -а 1 фазаларының айырмасына байланысты болатындығын атап өту қажет. cos + 1 ден артық және бірден кем бола алмайтындықтан, (4) формуладан қортқы амплитуда құраушы амплитудалардың қосындысынан артық, айырмасынан кем болмайтындығын, яғни ол мына аралықта болатындығын көруге болады:
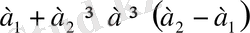
Егер құраушы тербелістер фазаларының айырмасы 0-ге немесе 2kπ (мұндағы k бүтін сан) тең болса, онда фазалар айырмасың косинусы +1 - ге тең болады, сонда (4) формула бойынша мынау шығады. :
 , бұған
, бұған
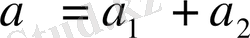 , яғни қортқы тербелістің амплитудасы фазалары айырмасы
, яғни қортқы тербелістің амплитудасы фазалары айырмасы
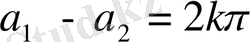 (мұндағы k=0, 1, 2,, 3, …. ) болғанда құраушы тербелістің а
1
және а
2
амплитудаларының қосыедысына тең болады. Құраушы тербелістердің фазалар айырмасы π- дің тақ санына тең болса онда фазадар айырмасының косинусы 1- ге тең болады және амплитуданың мәні (4) формула бойынша мынаған тең болады :
(мұндағы k=0, 1, 2,, 3, …. ) болғанда құраушы тербелістің а
1
және а
2
амплитудаларының қосыедысына тең болады. Құраушы тербелістердің фазалар айырмасы π- дің тақ санына тең болса онда фазадар айырмасының косинусы 1- ге тең болады және амплитуданың мәні (4) формула бойынша мынаған тең болады :
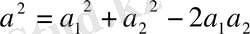 ,
,
Бұдан
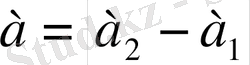
Мұнда
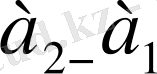 айырмасының абсолют мәнін алып отырмыз, өйткені жалпы амплитуданың өз мағнасы бойынша тек оң шама ғана бола алады.
айырмасының абсолют мәнін алып отырмыз, өйткені жалпы амплитуданың өз мағнасы бойынша тек оң шама ғана бола алады.
Осыдан қортқы тербелістің амплитудасы фазалар айырмасы
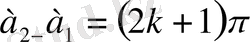
Болғанда құраушы тербелістердің амплитудалары айырмасының абсолют мәніне тең болады. Құраушы тербелістердің периодтары әртүрлі болып, бағыттары бір болсын . Сонда тербелістердің векторлық диаграммасында құраушы амплитудалардың векторлары әртүрлі бұрыштық жылдамдықпен айналады, осының салдарынан олардың арасындағы бұрыштың шамасы тұрақты болмайды, уақыт өтуімен бірге өзгеріп отырады . Осының нәтижесінде қортқы амплитуданың шамасы да өзгереді. Құраушы тербелістердің дөңгелектік жиілігі ω 1 және ω 2 болсын . Құраушы тербелістер фазаларының айырмасы өзгеріп отыратындықтан бастапқы уақыт кезеңі ретінде екі тербелістің бастапқы фазалары тең болатын уақыт кезеңін алуға болады, яғни тербелістерді мына жазуға болады:
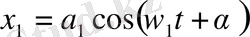
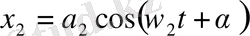 (7)
(7)
Мұнда
 деп жобалаймыз.
деп жобалаймыз.
Құраушы амплитудалар фазаларының айырмасы (
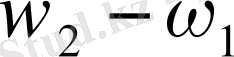 ) t болады. Фазалар айырмасының бұл мәні (4) формулаға қойсақ қортқы амплитуда квадратыынң мынадай мәні шағады :
) t болады. Фазалар айырмасының бұл мәні (4) формулаға қойсақ қортқы амплитуда квадратыынң мынадай мәні шағады :
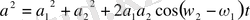 (8)
(8)
Сонымен қортқы тербелістің а амплитудасының шамасы уақытқа байланысыты белгілі периодпен өзгеріп отырады.
Қортқы амплитуда векторының бұрыштық айналыс жылдамдығы тұрақты болмайды сндықтан қортқы қозғалыс гормониялық тербеліс болмайды.
Амплитудалары (а 1 =a 2 ) периодтарының және дөңгелектік жиіліктерінің бір- бірінен айырмашылықтары аз болатын екі тербелістің қосу нәтежесін әдейілеп қарастыралық. (8) формуладағы а 1 =a 2 деп алсақ былай болады

Немесе
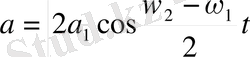 (9)
(9)
Мұнда теңдіктің оң бөлігіндегі шаманың абсолют шамасын аламыз, өйткені амплитуда тек оң шама ғана бола алады. Косинустың абсолют мәнінің периоды π - ге тең, олай болса амплитуданың абсолют шамасының өзгеру периоды косинустың аргументі π-ге өзгеретін уақыт аралығы болып табылады. :
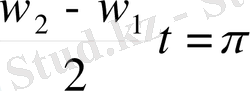
Бұдан
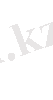
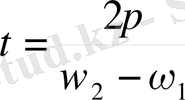 (10)
(10)
Яғни қорытқы тербеліс амплитудасының өзгеру жиілігі құраушы тербелістер жиіліктерінің айырмасына тең болады. Қорытқы амплитуданың х осімен жасайтын бұрышы
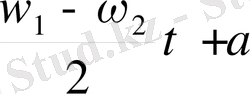
Тең көруге болады. Олай болса бұл жағдайда қорытқы амплитуданың векторы құраушы тербелістердің дөңгелектік жиіліктері қосындысының жартысына тең болатын тұрақты бұрыштық жылдамдықпен айналады. Егер қорытқы амплитуда векторының х осіне түсірілген проекциясын алатын болсақ, онда қорытқы қозғалыс шығады, бұдан х қорытқы ауытқуы мынаған тең болады.
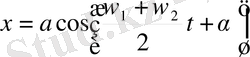
Немесе (9) формула бойынша
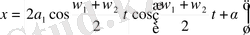
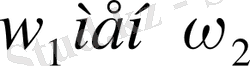 мәндері шамалас деп алғандықтын
мәндері шамалас деп алғандықтын
 шамасы
шамасы
 шамасынан кіші болады. Бұдан мынау шығады : қорытқы тербелісті дөңгелектік жиілігі
шамасынан кіші болады. Бұдан мынау шығады : қорытқы тербелісті дөңгелектік жиілігі
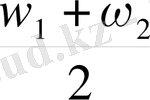 амплитудасы болатын гармониялық тербелмелі қозғалыс деп қарастыруға болады., бірақ сонда амплитуда тұрақты болмайды (9) бойынша уақытқа байланысты периодты болып баяу өзгереді. Амплитуданың (10) формуламен өрнектелген. Мұндай тербеліс 1- суретте графикпен көрсетілген. Бұл тербелістін амплитудасы біресе өседі біресе кемиді, бұл құбылыс соғу деп аталады.
амплитудасы болатын гармониялық тербелмелі қозғалыс деп қарастыруға болады., бірақ сонда амплитуда тұрақты болмайды (9) бойынша уақытқа байланысты периодты болып баяу өзгереді. Амплитуданың (10) формуламен өрнектелген. Мұндай тербеліс 1- суретте графикпен көрсетілген. Бұл тербелістін амплитудасы біресе өседі біресе кемиді, бұл құбылыс соғу деп аталады.
0
t
1 - сурет.
§. 1. 2. Өшетін тербелістер, автотербелістер.
Іс жүзінде материалдық нүктенің қандай да болмасын тербелісі, сырттан бір әсер болмаса өшіп қалады. Уақыт өтуімен бірге оның тербеліс амплитудасы азаяды. Тербелістің өшуіне қозғалысты бәсеңдететін күш, мысалы маятниктің тербелісі кезінде оның ілінген жерінің үйкеліс күші немесе ортаның кедергі кұші себеп болады. Біз нүктенің тек ортадағы түзу сызықтың бойымен тербелісін қарастырайық. Ортаның кедергі күші нүктенің қозғалыс жылдамдығына байланысты болады және жылдамдықтар шамасы аз болған жағдайда, оның жылдамдыққа пропорционал деп есептеуге болады. Ол күштің бағыты жылдамдықиың бағытына қарама - қарсы болады, сонымен, кедергі күшін - rx деп алуға болады. Мұндағы r тұрақты шама, ол кедергі коэффициенті деп аталады. Бұл күш - kx серпімді күшке қосылып бұдан нүктеге әсер ететін толық күш :
f= - kx - rx болады.
өзгеру периоды мынаған тең:
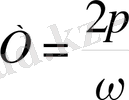
Немесе ω - ның орнына оның
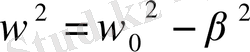
Мәнін қойсақ, мынаған тең болады:
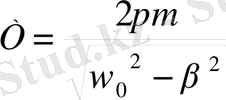
өрнекті пайдалаынып Т тербеліс периодын мына түрде жазуға болады:

Тербеліс периоды
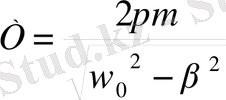
Кедергісі жоқ ортадағы массасы сондай нүктеге
F=-kx
Серпімді күштің әсерінен болатын тербеліс
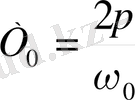
Периодынан үлкен болады. Х - тің уақытқа байланысты болу графигі 2 - суретте көрсетілген. Бұдан тербелыстің бірте-берте өшетінін көруге.
х
t
2-сурет. Өшетін тербелістер.
Бір - бірінен қашықтығы Т периодына тең болатын амплитудалардың тізбектес екі мәні қатынасынын логарифмі тербеліс өшуінің логарифмдік декременті деп аталады.
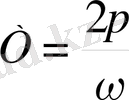
Өшетін тербелістер үшін мынадай өрнек шығады:
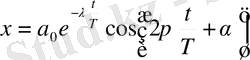
Тербеліс шексіз уақыт өткенде ғана тоқтайды, ал шынында ол шектеулі уақыт өткен соң тоқтайды. өйткені амплитуда атом өлшемдерімен шамалас болғанда макраскопиялық системаның тұтас система ретінде тербелуі мүмкін ем ес . Тербелістер өшетін жағдайда системаны тепе - теңдік қалыптан шығару үшін берілген энергия аз - аздап үйкеліс күшін жеңу үшін істелетін жұмысқа жұмсалады. Тербелістің өшпеуі үшін системаға сырттан үздіксіз энергия беріліп отыру қажет.
Үйкеліс күшінің болуна қарамастан, сырттан беріліп отырған энергия есебінен амплитудасын өзгертпей тербелетін системаға сағаттың маятнигі мысал бола алады. Храпты механизм маятникті оның тербелісіне үйлестіріп қозғап қалып отырады. Сонда маятник энергияны не біртіндеп босап жазылып отыратын пружинаның не төмен қарай түскен жүк энергиясының есебінен алады.
Осындай өзінің тербеліс амплитудаларын өзгертпейтін система автотербелмелі система деп аталады.
Өшетін тербелістер жөнінде нақты түсінік беру үшін мынадай екі мысал қарастырайық :
Бірінші мысал: маятник тербелісінің логарифмдік декременті
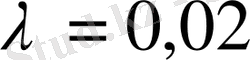 . маятник 100 рет толық тербелген соң тербеліс амплитудасы неше есе азаятындығын анықтайық.
. маятник 100 рет толық тербелген соң тербеліс амплитудасы неше есе азаятындығын анықтайық.
Шещуі: бастапқы t=0 болған уақыт кезеңінде
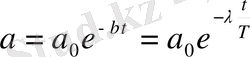
Тербеліс амплитудасы а=0 болады. Маятник 100 рет тербелген соң, яғни t=100T болған кезде тербеліс амплитудасы мынаған тең болады.
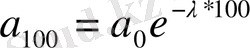 бұдан:
бұдан:
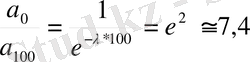
Яғни маятник 100 рет тербелгенде тербеліс амплитудасы 7, 4 есе азаяды.
Екінші мысал: ұзындығы l=50 см маятник 8 минут тербелгенде өзінің энергиясының 99 % жоғалтады. Маятниктің өшетін тербелістерінің логарифмдік декрементін білу керек .
Шешуі: маятниктің бастапқы уақыт кезеңіндегі тербеліс энергиясының Е 0 деп ал оны t=8 минут уақыт өткеннен кейынгі тербеліс энергиясын Е t деп белгілейік . Сонда есептең шарты бойынша
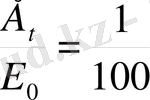
Тербеліс энергиясы амплитуданың квадратына тура пропорционал болғандықтан:

t=0 болған бастапқа уақыт кезенінде амплитуда а 0 - ге тең.
t уақыт өткеннен кейінгі амплитуда мынаған тең болады:
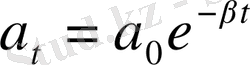
Мұндағы t маятниктің тербеліс периоды. Бұдан
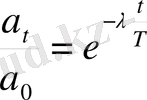
Ал ізделіп отырған тербелыстің өшу декременті
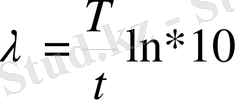
Тербеліс бірте - бірте өшетін болғандықтан маятиктің тербеліс периодының кәдімгі формуласын пайдаланып, Т тербеліс периодын жуық түрде былай жазуға болады:
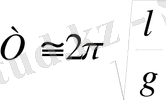
Сонда :
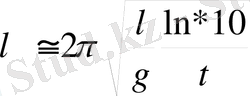
§. 1. 3. Мәжбүр тербелістер.
Материалдық нүктеге серпімді күш пен кедергі күштен басқа қосымша бір периодты күш әсер еткенде сол нүкте қандай тербеліс жасайтынын қарастырайық. Мысалы : пружинаға ілулі тұрған жіпті тең уақыт аралықтары өткен сайын қосымша бір күш қозғап қойып отырсын. Бұл мәжбүр етуші f 1 қосымша күш уақыт өтумен бірге синус немесе косинус заңы бойынша өзгеріп тұрады дейік, яғни f 1 күші былайша өрнектелсін
f 1 = H cos ωt (1)
мұны былай түсіну керек. Күш уақытқа байланысты периодты түрде
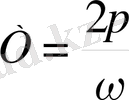
Периодпен өзгереді. Мұндағы Н шамасы күш амплитудасы деп аталады және күштің ең үлкен мәнін көрсетеді.
Мұндағы Н шамасы күш амплитудасының нүкте массасына қатынасына тең.
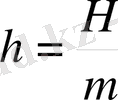 (2)
(2)
Мәжбүр етуші күш пен үйкеліс күші жоқ болса онда нүкте ω 0 дөңгелектік жиілікпен тербеледі.
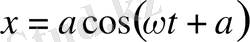 (3)
(3)
Барлық күштердің әсер етуінің нәтижесінде, периодты мәжбүр етуші күштің периодына тең тербеліс пайда болады.
Егер алғашқы кезде дене тыныштық қалыпта тұрып содан кейін оған
f 1 = H cos ωt
мәжбүр етуші күш әсер ете бастаған болса, онда дене мәжбүр тербелістер жасай бастайды. Бұл тербелістердің амплитудасы, анықталатын мәнге жеткенге дейін, арта береді. Мәжбүр тербелістердің а амплитудасы, α фазасы мәжбүр етуші күштің ω жиілігі мен нүктенің меншікті тербелістерінің ω
0
жиілігінің арасындағы қатыстарға тәуелді екенді. Жалпы аоғанда, тербеліс пен күш фазалас болмайды, яғни әсер етуші күш ең зор болған кезде нүктенің ауытқу шамасы ең үлкен мәніне жетпейді. Егер ортаның мәні, яғни кедергісі 0-ге тең болса онда тербеліс пен күштің фазалары бірдей болатындығын, барлық басқа жағдайларда фаза
 . тербелістер амплитудасы күш амплитудасына пропорционал болады. Егер меншікті тербелістердің жиілігі тұрақты болғанда мәжбүр етуші күштің жиілігі өзгеретін болса, онда бұл жағдайда мәжбүр тербелістердің амплитудасы өзгереді. Мәжбүр етуші күштің ω
рез
жиілігі
. тербелістер амплитудасы күш амплитудасына пропорционал болады. Егер меншікті тербелістердің жиілігі тұрақты болғанда мәжбүр етуші күштің жиілігі өзгеретін болса, онда бұл жағдайда мәжбүр тербелістердің амплитудасы өзгереді. Мәжбүр етуші күштің ω
рез
жиілігі
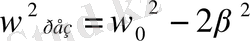
қатысын қанағаттантыратын болғанда мәжбүр тербелістер амплитудасы максимум мәніне жететіндігін көрсеиуге болады. Осындай максимум мәнінің пайда болуы резонанс құбылысы болып табылады. Жоғарыда шыққан қатыста резонанстан жиілік
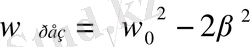
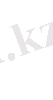
Формула бойынша максималь (резонанстық) амплитуда мынадай мәнге жетеді.

Егер ортаның кедергісі 0-ге тең, яғни β=0 болса сонда
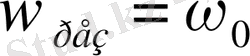
Болған кезде амплитуда максимум болады, яғни мәжбүр етуші күштің ω жиілігі мекшікті тербелістердің ω 0 жиілігіне тең болса, онда мәжбүр тербелістердің амплитудасының шамасы шексіз үлкен болады. β - ның 0-ден басқа мәндерінде амплитуда еш уақытта шексіз болмайды және ол максимум мәнде ω рез -ның ω 0 -ден кіші мәндерінде жетеді. Мәжбүр тербелістер амплитудасының мәжбүр етуші күштің жиілігіне тәуелділігі . β - ның әртүрлі мәндері үшін 3- суреттен көрсетілген бұдан неғұрлым . β - ның өшу коэффициенті үлкен болса, амплитуданың максимум мәнін көрсететін сызық соғұрлым сүйірлене түсетінін көреміз.
А/h
10
9
8
7
6 β =0, 05 ω 0
5
4
3
2 β=0, 25ω 0
1 β= ω 0 3-сурет.
0
0, 2 0, 6 1, 0 1, 4 1, 8 2, 0
Суреттегі қисық сызықтар резонанс қисықтары деп аталады. Резонанс болатын система тербелісінің β өшу коэффициенті неғұрлым аз болса, резонанс қисығын соғұрлым биік және сүйір болады. шынында да, әрқашан β 0 -ге тең болмайтындықтан резонанс болған кезінде амплитуда шексіз үлкен бола алмайды.
Мәжбүр тербелістер базасы α -ның жиілікке тәуелділігін қарастырайық.
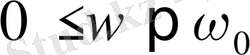 болғанды тангенс мәндері теріс болады, демек α -ның мәні үшін мынадай екі теңдік шығады:
болғанды тангенс мәндері теріс болады, демек α -ның мәні үшін мынадай екі теңдік шығады:
 немесе
немесе
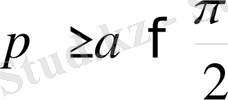
Теңдеуді ω=0 деп алсақ, сонда
 болады, ал α мен h амплитудалар оң шама болғандықтан, ω=0 болғанда cos α да 0-ден артық болуы қажет. Бұл щарт әрбір екі теңсіздіктің біреуін таңдап алуға мәжбүр етеді.
болады, ал α мен h амплитудалар оң шама болғандықтан, ω=0 болғанда cos α да 0-ден артық болуы қажет. Бұл щарт әрбір екі теңсіздіктің біреуін таңдап алуға мәжбүр етеді.
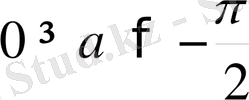 сонымен
сонымен
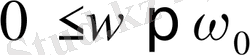 болғанда фазалар айырмасы α теріс болады, яғни мәжбүр тербелістер мәжбүр етуші күштен фаза жағынан кейін қалып отырады. ω -ның мәні резонанстық
болғанда фазалар айырмасы α теріс болады, яғни мәжбүр тербелістер мәжбүр етуші күштен фаза жағынан кейін қалып отырады. ω -ның мәні резонанстық
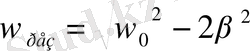
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz