Тең қуатты жиындар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Тең қуатты жиындар

Х - қайсыбір топ оқушыларының және У - осы топ оқитын аудиториядағы орындықтар жиындары берілген. Осы жиындарды элементтерінің сандары бойынша салыстыру керек болсын. Мұны екі түрлі тәсілмен жүргізуге болады. Біріншіден, оқушыларды орындықтарды санап, олардың сандарын салыстыруға болады. Бірақ басқаша да істеуге болады. Әрбір оқушыны бір орындыққа отырғызамыз. Осылай еткенде, егер барлық барлық оқушыларға орын табылып, бірде - бір бос орындық қалмаса, онда ол Х және У жиындарының элементтерінің сандары тең екендігін көрсетеді.

Басқа сөзбен айтқанда, Х және У жиындарын екінші тәсілмен салыстырып, біз Х жиынын У жиынына өзара бірмәнді бейнелеу бар екендігін анықтадық.

Сонымен, екі жиынды салыстырудың бірінші тәсілі - олардың элементтерінсанауда жатыр. Әрине бұл тәсілді жиындардың элементтерінің сандары шектеулі болған жағдайда ғана қолдануға болады. Екінші тәсілдің негізі бір жиынды екінші жиынға өзара бірмәнді түрде бейнелеуде жатыр. Бұл тәсілді шектеулі де және шектеусіз де жиындарға қолдануға болады.

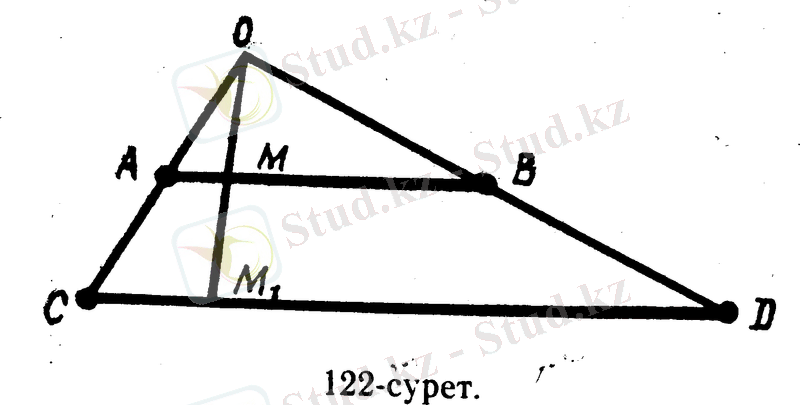
АВ кесіндісінің нүктелерінің жиыны Х, СD кесіндісінің нүктелерінің жиыны У болсын. Кесінділердің ұзындықтары әр түрлі(1 - сурет) . Осы кесінділердің шеткі А мен С, В мен D нүктелерін түзумен қосамыз. Сонда О нүктесі осы түзулердің қиылысу нүктесі болады. АВ кесіндісінің кез келген бір М нүктесін алайық. Оны О нүктесімен түзу арқылы қосамыз. Осы түзу СD кесіндімен бір М ₁ нүктесінде қиылысады. Осылай алынған М ₁ нүктесін АВ кесіндісінің М нүктесіне сәйкес қоямыз.

Осылай құрудан АВ кесіндісінің әрбір нүктесіне СD кесіндісінің тек бір ғана нүктесінің сәйкес келетін және СD әр түрлі екі нүктесіне АВ кесіндісінің әр түрлі екі нүктесі сәйкес келетінін байқаймыз.

Ендеше, АВ кесіндісінің нүктелерінің жиыны Х - тың СD кесіндісінің нүктелерінің жиыны У - ке өзара бірмәнді бейнелеу екендігі шығады.

Сонымен, егер Х және У жиынына өзара бірмәнді бейнелеуге болатын болса, онда Х және У екі жиынын тең қуатты жиындар деп атайды.

Егер Х және У жиындары тең қуатты болса, онда оны Х ~ У түрінде жазады. Бұл жазуды « Х және У жиынына тең қуатты » деп оқиды.

Мысалы, АВС үшбұрышының қабырғаларының жиыны мен оның бұрыштарының жиыны тең қуатты, сол сияқты АВ кесіндісінің (1 - сурет) нүктелерінің жиыныда тең қуатты болады.

Тең қуатттылық ұғымын шектеулі және шектеусіз жиындардың екеуіне де қолдануға болады. Әрі екі шектеулі жиын элементтерінің сандары тең болғанда, тек сонда ғана тең қуатты бола алады.

Шектеусіз жиындардың тең қуаттылығының мысалдарымен танысайық.

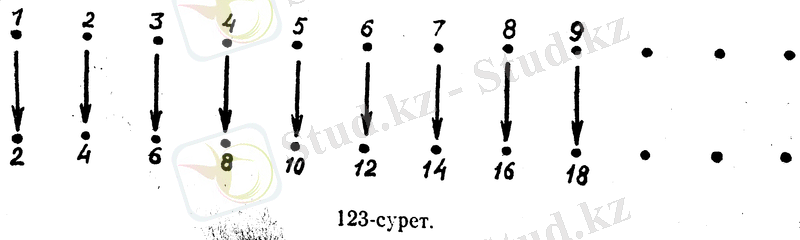
N - барлық натурал сандар жиынын және У барлық жұп натурал сандар жиынын алайық. Бұл екі жиынның екеуіде шетеусіз жиындар, әрі У жиыны N жиынынан алынған саннан 2 есе үлкен санды сәйкес қоямыз.

Осылай орнатылған сәйкестілік N жиынын У жиынына өзара бірмәнді бейнелеу болып табылады. Өйткені, әрбір натурал, x N саны сәйкес келеді және керісінше. Сонымен, барлық натурал сандар жиыны N барлық жұп натурал сандар жиыны У - ке тең қуатты екен, яғни N ~ У.

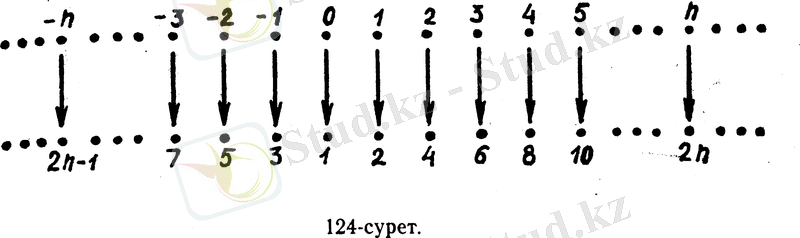
Барлық натурал сандар жиыны N және барлық бүтін сандар жиыны арасында 3 - суретте көрсетілгендей, яғни әрбір оң бүтін санға жұп натурал санды, ал әрбір теріс бүтін санға тақ натурал санды сәйкес қоямыз.

Бұл сәйкестіліктің өзара бірмәнді екенін көреміз, ендеше, Z ~ N.

Барлық рационал сандар жиыны Q және барлық натурал сандар жиыны N тең қуатты жиындар екендігі дәлелденген, яғни Q ~ N.

Барлық натурал сандар жиынына тең қуатты шектеусіз жиын саналатын жиын деп аталады.

Мысалы, барлық бүтін сандар жиыны, барлық рационал сандар жиыны, осы жиындардың кез келген шектеусіз ішкі жиындары, натурал сандар жиынының шектеусіз ішкі жиындары - барлығы да саналатын жиындар болып келеді.

«Жалпы санауға болмайтын жиындар бола ма? » деген сұрақ туады.

Бұл сұраққа мына кері теорема жауап береді: Ноль мен бірдің арасындағы нақты сандар жиыны саналмайтын жиын(теореманың бұл жерде дәлелдеуін келтірмейміз) . Мынадай жиындардың:

а) барлық нақты сандар жиыны

б) түзу бойындағы нүктелер жиыны;

в) жазықтықтағы нүктелер жиыны әрқайсысы ноль мен бірдің арасындағы нақты сандар жиынына тең қуатты екенін дәлелдеуге болады. Олай болса, олар санауға келмейтін жиындар.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.