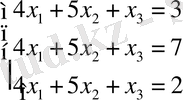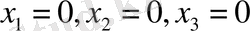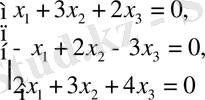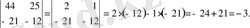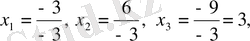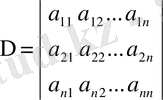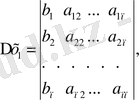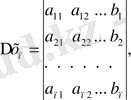Сызықтық теңдеулер жүйесін шешудің Крамер формуласы: теориясы және қолданылуы


Жоспар:
- Сызықтық теңдеулер жүйесін шешудің Крамер формуласы туралы түсінік.
- Үш белгісізді сызықтық үш теңдеу жүйесі.
- пбелгісіздіпсызықтық теңдеу жүйесі.
- Мысалдар.
Сызықтық теңдеулер жүйесін шешудің Крамер формуласы.
Сызықтық теңдеулер жүйесі жалпы жағдайда мына түрде жазылады:
(15)
Мұндағы
х
1
, х
2
, . . . , х
п
белгісіздерінің орнына қойғанда барлық теңдеулерді тепе-теңдікке айнадыратын
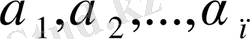 сандарын (13) жүйенің шешімі деп аталады.
сандарын (13) жүйенің шешімі деп аталады.
Теңдеулер жүйесінің ең болмағанда бір шешімі бар болса, онда жүйе үйлесімді , шешімі жоқ болса, үйлесімсіз деп аталады. Үйлесімді жүйенің бір ғана шешімі болса, онда ол жүйе анықталған, ең болмағанда әртүрлі екі шешімі болса, онда жүйе анықталмаған деп аталады.
Айталық, х 1 , х 2 және х 3 үш белгісізді сызықтық үш теңдеу системасы
(16)
берілсін, мұнда коэффициенттер
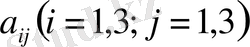 мен бос мүшелер
мен бос мүшелер
 - белгілі нақты сандар деп есептейміз.
- белгілі нақты сандар деп есептейміз.
(16) система шешімі деп ондағы
х
1
, х
2
, х
3
белгісіздердің орнына сәйкесінше
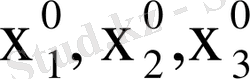 сандарын қойғанда ол системаның әрбір теңдеуін теңбе-теңдікке айналдыратын (
сандарын қойғанда ол системаның әрбір теңдеуін теңбе-теңдікке айналдыратын (
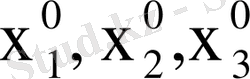 ) сандар үштігін атайды. (16) система шешімдерін табу мәселесін қарастырайық.
) сандар үштігін атайды. (16) система шешімдерін табу мәселесін қарастырайық.
Мынадай белгілеулер енгізейік
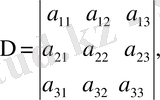
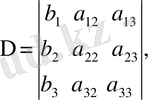
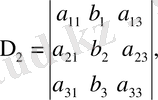
(17)
(16) система теңдеулерін сәйкес түрде алгебралық А 11 А 21 А 31 толықтауыштарға көбейтіп нәтижелерін қоссақ, мына теңдеу шығады
(а 11 А 11 +а 21 А 21 +а 31 А 31 ) х 1 +(а 12 А 11 +а 22 А 21 +а 32 А 31 ) х 2 +
+(а 13 А 11 +а 23 А 21 +а 33 А 31 ) х 3 =b1A 11 +b 2 A 21 +b 3 A 31 . (18)
Бұл теңдеуде
х
1
-дің коэффициенті
 -ға тең, өйткені ол -
-ға тең, өйткені ол -
 анықтауышының бірінші бағанының элементтері бойынша жіктелуі. Ал
х
2
мен
х
3
-тің коэффициенттері ноль-ге тең, өйткені олар сәйкес түрде екінші және үшінші бағандардың элементтері мен бірінші баған элементтерінің алгебралық толықтауыштарына көбейтінділерінің қосындысына тең. (18) -дің оң жағы
анықтауышының бірінші бағанының элементтері бойынша жіктелуі. Ал
х
2
мен
х
3
-тің коэффициенттері ноль-ге тең, өйткені олар сәйкес түрде екінші және үшінші бағандардың элементтері мен бірінші баған элементтерінің алгебралық толықтауыштарына көбейтінділерінің қосындысына тең. (18) -дің оң жағы
 анықтауышына тең. Сонымен,
х
3
және
х
2
белгісіздерінен арылған (18) теңдеу мына түрге келеді
анықтауышына тең. Сонымен,
х
3
және
х
2
белгісіздерінен арылған (18) теңдеу мына түрге келеді
. (19)
Осыған ұқсас түрде алдымен х 1 мен х 3 -тен, одан кейін х 1 мен х 2 -ден арылып, мына теңдеулерді шығарып аламыз
(20)
Сонымен, (16) системадан, (19) бен (20) ескерсек, мына система шығады
(21)
(21) система (16) системаның салдары болып табылады. Сондықтан (16) системаның әрбір шешімі (егер ол бар болса) (21) системаның да шешімі болады. Үш жағдай болуы мүмкін.
1)
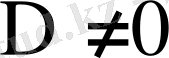 , сонда (21) системаның (сондай-ақ (16) системаның да) бір ғана шешімі болады да, ол Крамер формулалары делінетін мына формулалар бойынша анықталады
, сонда (21) системаның (сондай-ақ (16) системаның да) бір ғана шешімі болады да, ол Крамер формулалары делінетін мына формулалар бойынша анықталады
(22)
2)
 ал
ал
 анықтауыштарының кем дегенде бірі нольден өзгеше болсын. Сонда (21) системаның кем дегенде бір теңдеуінің бірде-бір шешімі болмайды, демек, (21) және (16) системалардың да бірде-бір шешімі болмайды.
анықтауыштарының кем дегенде бірі нольден өзгеше болсын. Сонда (21) системаның кем дегенде бір теңдеуінің бірде-бір шешімі болмайды, демек, (21) және (16) системалардың да бірде-бір шешімі болмайды.
3)
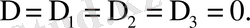 Бұл жағдайда системаның шешімдері атымен болмауы да мүмкін. Мысалы, мына системаның
Бұл жағдайда системаның шешімдері атымен болмауы да мүмкін. Мысалы, мына системаның
бірде-бір шешімі болмайды. Оның
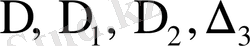 анықтауыштарының барлығы да нольге тең болады.
анықтауыштарының барлығы да нольге тең болады.
Дегенмен, егер системаның кем дегенде бір шешімі бар болса, оның шексіз көп шешімдері болады. Бұл тұжырымның дәлелдемесіне тоқталмаймыз.
Мына түрдегі теңдеулер системасы
(23)
б і р т е к т і с ы з ы қ т ы қ с и с т е м а деп аталады. Ол (16) системаның
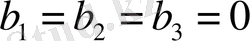 болғандағы дербес жағдайы. Мына
болғандағы дербес жағдайы. Мына
(24)
үш сан (23) системаны қанағаттандыратындығы айқын. (24) шешім нольдік шешім деп аталады. Жалпы алғанда (23) системаны кем дегенде бірі нольден өзге сандар үштіктері де қанағаттандыруы мүмкін. Мұндай шешімдер нольдік емес шешімдер деп аталады,
Мынадай тұжырым орынды.
Егер біртекті
(23)
системаның анықтауышы нольге тең болмаса
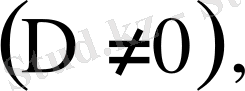 оның тек нольдік қана шешімі болады.
оның тек нольдік қана шешімі болады.
Шынында да, анықтауыштардың 2) қасиеті бойынша
 анықтауыштарының барлығы да нольге тең болады. Сонда Крамер формулалары (22) бойынша
анықтауыштарының барлығы да нольге тең болады. Сонда Крамер формулалары (22) бойынша
(23) сисеманың жалғыз ғана шешімі болады.
1-мысал. Біртекті мына системаның
тек нольдік шешімі
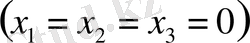 болатындығын тексеру керек.
болатындығын тексеру керек.
Осының алдындағы тұжырымға сүйеніп, біртекті системаның анықтауышы
 нольге тең еместігін көрсету жеткілікті
нольге тең еместігін көрсету жеткілікті
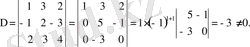
Е с к е р т у.
 анықтауышын есептегенде алдымен бірінші бағанда нольдер шығарып алдық. Ол үшін бірінші жолдың элементтерін екінші жолдық сәйкес элементтеріне қосып, одан соң бірінші жолдың элементтерін (-2) -ге көбейтіп, үшінші жолдың сәйкес элементтеріне қостық. Анықтауыштың шамасы өзгерген жоқ. Осыдан кейін шыққан анықтауышты бірінші бағанның элементтері бойынша жіктедік. Ақтығында, есеп екінші ретті бір ғана анықтауышты есептеуге келтірілді.
анықтауышын есептегенде алдымен бірінші бағанда нольдер шығарып алдық. Ол үшін бірінші жолдың элементтерін екінші жолдық сәйкес элементтеріне қосып, одан соң бірінші жолдың элементтерін (-2) -ге көбейтіп, үшінші жолдың сәйкес элементтеріне қостық. Анықтауыштың шамасы өзгерген жоқ. Осыдан кейін шыққан анықтауышты бірінші бағанның элементтері бойынша жіктедік. Ақтығында, есеп екінші ретті бір ғана анықтауышты есептеуге келтірілді.
2-мысал. Крамер формулалары бойынша мына системаны
шешу керек.
Бұл системаның анықтаушы
 =-3 (1-мысалды қараңыз),
=-3 (1-мысалды қараңыз),
 анықтауыштарын есептейік.
анықтауыштарын есептейік.
 есептеуді түсіндіре кетейік. Агдің бірінші жолының элементтерін 14-ке және (-8) -ге көбейтіп нәтижелерін екінші және үшінші жолдардың сәйкес элементтеріне қостық. Нәтижеде жаңа анықтауыш шықты, ол берілген
есептеуді түсіндіре кетейік. Агдің бірінші жолының элементтерін 14-ке және (-8) -ге көбейтіп нәтижелерін екінші және үшінші жолдардың сәйкес элементтеріне қостық. Нәтижеде жаңа анықтауыш шықты, ол берілген
 анықтауышқа тең, (8) қасиет бойынша оның бірінші бағанында екі ноль бар. Одан кейін оны бірінші бағанның элементтері бойынша жіктедік ((9) формулалардың біріншісі бойынша) . Сөйтіп, есепті екінші ретті анықтауышты
анықтауышқа тең, (8) қасиет бойынша оның бірінші бағанында екі ноль бар. Одан кейін оны бірінші бағанның элементтері бойынша жіктедік ((9) формулалардың біріншісі бойынша) . Сөйтіп, есепті екінші ретті анықтауышты
есептеуге келтірдік. Оны тікелей есептеуге болады. Дегенмен, мұны да жеңіл жолмен есептеуге болады. Ол үшін екінші жолдың элементтерін 2-ге көбейтіп, бірінші жолдың сәйкес элементтеріне қосу керек, сонда шығатын анықтауыш оңай есептеледі
 2
және
2
және
 3
анықтауыштары осылайша есептеледі:
3
анықтауыштары осылайша есептеледі:
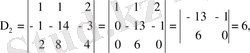

Олай болса, -
яғни (1, -2, 3) -система шешімі.
п белгісізді п сызықтық теңдеу жүйесі.
(25)
Мұны қысқаша
(i=1, …, n) түрінде жазамыз.
Бұл жүйені шешу үшін a ij сандарынан құралған жүйенің анықтауышын есептейміз.
Айталық,
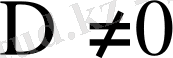 делік. Бұл жағдайда жүйенің шешімі бар және жүйе анықталған екендігін дәлелдеуге болады. Шешімді мына әдіспен:
делік. Бұл жағдайда жүйенің шешімі бар және жүйе анықталған екендігін дәлелдеуге болады. Шешімді мына әдіспен:
(26)
яғни Крамер формулаларымен тауып аламыз. Мұндағы
яғни і -інші бағанды бос мүшелермен ауыстырудан алынған анықтауыш.
Крамер әдісі.
п белгісіз бар біртекті емес п сызықты теңдеулер жүйесін қарастырайық:
(27)
Берілген жүйенің белгісіздер саны теңдеулер санына тең, жүйенің негізгі матрицасы п жатық, п - тік жолдардан тұрады. Сондықтан жүйенің негізгі матрицасы п - ретті квадрат матрица
(28)
А матрицаның анықтауышы берілген сызықты теңдеулер жүйесінің анықтауышы нөлге тең болмасын, яғни
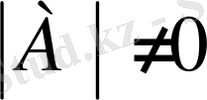 .
.
Крамер әдісімен (28) жүйенің шешімін іздістірместен бұрын төмендегі шартты белгілеуге келісіп алайық.
Берілген жүйенің
(29)
анықтауышының бірінші тік жолының элементері х 1 белгісіздің коэффициенттері, ал екінші тік жолдың элементтері х 2 белгісіздің коэффициенттері т. с. с. Осы анықтауыштың кез келген тік жолының мысалы, к - тік жолының элементерін (х к белгісізінің коэффициенттерін) (27) жүйенің сәйкес бос мүшелерімен орын алмастырғанда алынған анықтауышты
таңбасымен белгілейік:
(30)
3. 1 - теорема (Крамер теоремасы) . Егер (27) біртекті емес сызықты теңдеулер жүйесінің негізгі матрицасының анықтауышы нольге тең боламаса, онда ол анықталған жүйе. Бұл жүйенің шешімі Крамер формуласымен анықталады:
... жалғасы
(31)
Д ә л е л д е у. Ең алдымен, (27) жүйе үйлесімді деп (28) формуланы дәлелдейік. Ол үшін, х 1 , х 2 . . . , х п сандары берілген жүйенің шешімі болсын.
анықтауышының k - тік жолының элементтерін x k - ға көбейтейік (анықтауыштың 1- қасиеті) :
(32)
Бұл анықтауыштың бірінші тік жолын х 1 - ге, екінші тік жолын х 2 - ге, т. с. с. п - тік жолын х п - ге көбейтіп ( k - тік жолын көбейтпейміз), k - тік жолын қосайық. Мұндай өрнектеу нәтижесінде анықтауыштың 1- қасиеті бойынша
x k анықтауышының мәні өзгермейді.
Сондай - ақ басқа тік жолдарының элементтері өзгермейді. Ал k -тік жолының бірінші элементі мына қосындыға
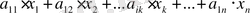
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz