Белгісіз шарттардағы шешім қабылдау: ойындар теориясы және үйлесімді стратегиялар


Қазақстан Республикасы Білім және ғылым министрлігі
Ы. Алтынсарин атындағы Арқалық мемлекеттік педагогикалық институты
Тақырыбы:
Орындаған: И-31 тобының студенті
Молдабекова М.
Тексерген: Утельбаева А.
Арқалық, 2009 ж.
Үйлесімді шешімдер теориясының бір мәселесі - шешімді белгісіз шарттарда қабылдау. Шешімнің негізделуі үшін ойындар теориясында қарастырылатын арнайы математикалық тәсілдер ойлап табылған. Ойындар теориясы жас математикалық дисциплиналар қатарына жатады. Оның пайда болуы 1944 жылғы Нейман мен Моргенштерннің «Экономикалық ұстаным және ойындар теориясы» атты монографиясының жарық көруімен байланысты. Кейінірек ойындар теориясы тәжірибелік мағызы бар математикалық жеке бағытқа айналып кетті.
Ойындар теориясы - бұл қатысушылардың қалаулары әр түрлі және мақсаттары әр түрлі жолдармен орналасатын математикалық модельдер теориясы. Қатысушылардың қалауларының қарама-қарсы қақтығысулары даулы (конфликті) жағдайға әкеліп соғады. Осындай жағдайларды сипаттау қажеттілігі, өз кезегінде, мақсаты дауға қатысушыларының мінез-құлқының рационалды ұсыныстарын қарастыру болып келетін ойын теориясының тууына әкеліп соқты.
Тәжірибелік даулы жағдайлардың сараптамасы кезінде көптеген ұсақ факторлардың нәтижесінде пайда болатын қиыншылықтарды жеңу үшін жағдайлардың қарапайымдалған моделі құрастырылады. Мұндай модель ойын деп аталады. Ойындық модельде даулы жағдай белгілі бір ережелер бойынша дамып отырады. Даулы жағдайлардың сараптамасының негізгі базасы ретінде кең таралған ойындар - шахмат, дойбы және карта ойындары қызмет етеді. Сондықтан ойын теориясына келесі терминология тән: «Ойыншылар» (дауға ұатысушы жақтар), «ұтыс» (даудың шешімі), т. б.
Ойынның нәтижесінің белгісіздігін әр түрлі себептердің арқасында үш топқа бөлуге болады:
1. Ойын ережесінің ерекшеліктері оның дамуында нәтижесінің алдын ала айту мүмкіндігі болмайтындай әр алуандылық тудырады. Мұндай түрдің белгісіздігінің көзі комбинаторикалық, ал сәйкес ойындар - дәл солай комбинаторикалық деп аталады. Мысалы ретінде шахмат ойынын алуға болады. Дегенмен, ойынның комбинаторикалық күрделілігі тиісті математикалық аппарат және есептеуіш техника қолдану арқасында тарихи өтпелі қасиетке ие. Камбинаторикалық ойынның бір реті үшін кішігірім көлемді мәселе есептерді шешу арқылы ұтысты комбинациялар ойлап табылған.
2. Белгісіздіктің келесі бір көзі - кездейсоқ факторлардың әсер етуі болып келеді. Барысы кездейсоқ себептер нәтижесінде белгісіз болып келетін ойындар құмар ойындар (сүйек ойыны, рулетка, т. б. ) деп аталады.
3. Белгісіздіктің үшінші көзі болып қарсыластың іс-қимылы жайлы, оның стратегиясы жайлы мәліметтердің жоқтығы болып табылады. Ойындардың мұндай түрі стратегиялық деп аталады.
Осы ойларды мұқият қарастырайық. Ойында екі немесе одан да көп қарсыластардың қалаулары қақтығысады. Бірінші жағдайда ой жұптық, ал екінші жағдайда көптік деп аталады. Үлкен тәжірибелік мәнге жұпты ойлар ие болғандықтан, тек қана соларды қарастырған тиімдірек. Ойыншыларды А және В деп белгілелік. Сонымен қатар, ойын дегенді А және В ойыншыларының анық белгіленген бір ережелері бойынша кезекті қимылдау тәсілдері деп түсінейік. Ережелер ойыншылар іс-қимылының мүмкін болатын нұсқаларын, әрбір жақтың қарсылас қимылы жайлы білетін мәліметтер көлемін, тиісті іс-қимылдар алып келетін ойын нәтижесін анықтайды. Көптеген ойындарда ойыншылардың қалауы мөлшерлік бағалауға, яғни ойын нәтижесін әлдебәр санмен анықтауға түсетіні беліглі. Ойын теориясындағы жүріс дегеніміз ой ережесі бойынша орындауға болатын бір қимылды таңдау және оны жүзеге асыру. Ойыншылардың стратегиясы деп ол мүмкіндік туған әрбір жағдайды және фактілік мүмкін болатын мәліметті тиімді таңдау жоспарын атайды. Ойыншылардың шешімді ой барысында қабылдайтыны анық. Дегенменғ теория жүзінде ойыншы осы шешімді алдын-ала қабылдайтынын болжауға болады. Онда осы шешімдер ара қатынасы оның стратегиясы болып табылады. Мүмкін болған стратегиялар санына байланысты ойындар шекті және шексіз болып бөлінеді. Ойын теориясының мақсаты - ойыншыларға ұсыныстар өңдеу, яғни олар үшін ең тиімді стратегияларды анықтау болып табылады. Оптимальді (тиімді) стратегия дегеніміз - ойынның бірнеше рет қайталануында берілген ойыншыны мүмкін болатын максималды орташа ұтыспен қамтамасыз ететін стратегия.
Стратегиялық ойынның ең қарапайым түрі - екі адамның 0-ге тең есеппен ойнауы (жақтардың ұтысының сомасы 0-ге тең) болып табылады. Ойын екі жүрістен тұрады:
1) А ойыншы өзінің бір мүмкін болатын стратегиясын
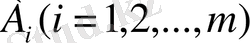 таңдайды, ал В ойыншы
таңдайды, ал В ойыншы
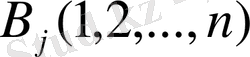 стратегиясын таңдайды, срнымен қатар әрбір таңдау келесі оыншының таңдауын білмейтіндей шарттармен өтеді.
стратегиясын таңдайды, срнымен қатар әрбір таңдау келесі оыншының таңдауын білмейтіндей шарттармен өтеді.
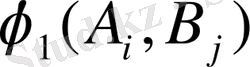 және
және
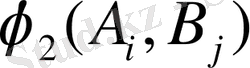 ұтыстарының нәтижесі әрбір ойыншыны, егер
ұтыстарының нәтижесі әрбір ойыншыны, егер
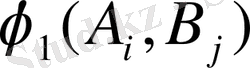 =
=
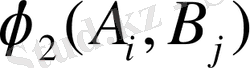 болғанда
болғанда
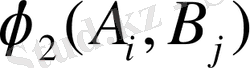
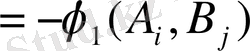 болатындай
болатындай
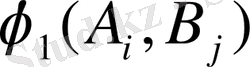
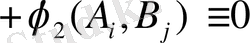 қатынасы қанағаттандырады. А ойыншының мақсаты
қатынасы қанағаттандырады. А ойыншының мақсаты
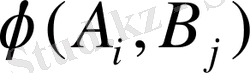 функциясын максималдау (жоғарылату) болса, өз кезегінде В ойыншының мақсаты осы функцияны минималдау (төмендету) болып тбылады. Ойыншының әрбірі функцияның мәні туіелдң болып келетін ауыспалыны таңдай алады. Егер А ойыншы стратегиясынан әлдебірін таңдаса, онда бұл өздігінен
функциясын максималдау (жоғарылату) болса, өз кезегінде В ойыншының мақсаты осы функцияны минималдау (төмендету) болып тбылады. Ойыншының әрбірі функцияның мәні туіелдң болып келетін ауыспалыны таңдай алады. Егер А ойыншы стратегиясынан әлдебірін таңдаса, онда бұл өздігінен
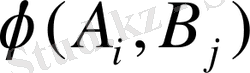 функциясының мәніне әсер ете алмайды.
А
і
-дің
функциясының мәніне әсер ете алмайды.
А
і
-дің
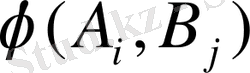 мәнінің көлеміне әсер етуі белгісіз болып табылады; белгісіздік
мәнінің көлеміне әсер етуі белгісіз болып табылады; белгісіздік
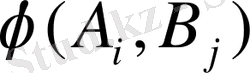 - ді минималдау қағидасынан шығып, басқа ойыншылардың
B
j
ауыспалысын таңдауынан кейінгі орында тұрады. Сонымен бірге
B
j
басқа ойыншылармен анықталады.
- ді минималдау қағидасынан шығып, басқа ойыншылардың
B
j
ауыспалысын таңдауынан кейінгі орында тұрады. Сонымен бірге
B
j
басқа ойыншылармен анықталады.
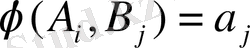 ге делік. А матрицасын құрайық.
ге делік. А матрицасын құрайық.
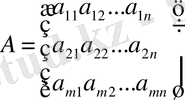
Матрицаның қатарлары
А
і
стратегиясына, ал бағандары
B
j
стратегиясына сәйкем келеді. А матрицасы
төлемді
немесе
ойын матрицасы
деп аталады.
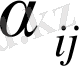 матицасының элементтері - А ойыншының ұтысы, егер ол
А
і
стратегиясын таңдаса, ал В ойыншысы
B
j
стратегиясын таңдайды. А ойыншысы әлдебір
А
і
стратегиясын таңдады делік, онда ең жаман жағдайда (мысалыға, таңдау жайлы В ойыншысы білсе), ол
матицасының элементтері - А ойыншының ұтысы, егер ол
А
і
стратегиясын таңдаса, ал В ойыншысы
B
j
стратегиясын таңдайды. А ойыншысы әлдебір
А
і
стратегиясын таңдады делік, онда ең жаман жағдайда (мысалыға, таңдау жайлы В ойыншысы білсе), ол
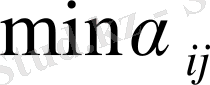 - ге тең ұтыс алады. Мұндай мүмкіндікті көріп тұрып А ойыншысы өзінің минимальді
- ге тең ұтыс алады. Мұндай мүмкіндікті көріп тұрып А ойыншысы өзінің минимальді
 ұтысын максималдауға болатындай стратегияны таңдау керек.
ұтысын максималдауға болатындай стратегияны таңдау керек.
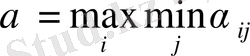 .
.
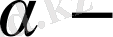 ның көлемі - А ойыншының кепілденген ұтысы -
ойынның төменгі құны
деп аталады.
ның көлемі - А ойыншының кепілденген ұтысы -
ойынның төменгі құны
деп аталады.
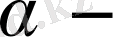 ны тудыратын
ны тудыратын
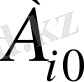 стратегиясы
максиминді
деп аталады.
стратегиясы
максиминді
деп аталады.
В ойыншысы стратегияны таңдай отырып, келесі қағидаға жүгінеді: әлдебір
B
j
стратегиясын таңдауда оның жеңілісі матрицаның
j
бағанының элементтерінің максимальді мәндерінен аспайды, яғни
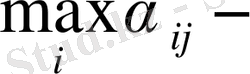 ге тең немесе кіші. Көптеген
ге тең немесе кіші. Көптеген
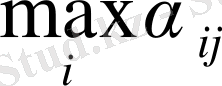 -ді
j
-дің әр алуан мәніне қарастыра отырып, В ойыншы оның максимальді
-ді
j
-дің әр алуан мәніне қарастыра отырып, В ойыншы оның максимальді
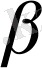 жеңілісі минималданатындай (төменденетіндей)
j мәнін
таңдайтыны анық:
жеңілісі минималданатындай (төменденетіндей)
j мәнін
таңдайтыны анық:
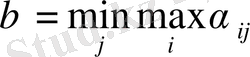
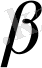 көлемі
ойынның жоғарғы құны
деп аталады. Ал
көлемі
ойынның жоғарғы құны
деп аталады. Ал
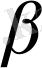 ұтысына сәйкес
ұтысына сәйкес
 стартегиясы
минимаксты
деп аталады.
стартегиясы
минимаксты
деп аталады.
А ойыншысының фактті ұтысы сыбайластарының есті қимылдарында ойынның төменгі және жоғарғы құнымен шектелген. Егер бұл мәнді
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz