Жазықтықтағы түзулер, екінші реттік қисықтар және кеңістіктегі беттердің теңдеулері


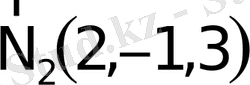 . Сонымен
. Сонымен
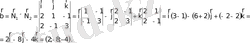
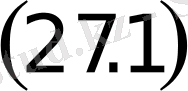 формулаға
формулаға
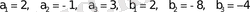 Equation. 3 мәндерiн қойып,
Equation. 3 мәндерiн қойып,
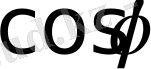 Equation. 3 -ы табамыз.
Equation. 3 -ы табамыз.
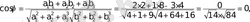
 осыдан
осыдан
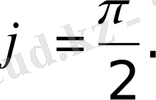
§28. Жазықтықтағы түзудiң теңдеулерi
 түзуi берiлсiн. Басы
түзуi берiлсiн. Басы
 нүктеде жатқан
нүктеде жатқан
 векторының соңғы нүктесiнен осыған перпендикуляр
векторының соңғы нүктесiнен осыған перпендикуляр
 тү-зуi жүргiзiлген (24-сурет) . Сондықтан
тү-зуi жүргiзiлген (24-сурет) . Сондықтан
 векторы
векторы
 түзуiн толық анықтайды.
түзуiн толық анықтайды.
 саны
саны
 вектордың ұзындығы
вектордың ұзындығы
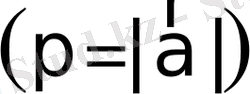 . Мұндағы
. Мұндағы
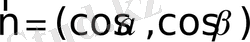 векторы
векторы
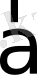 векторының бiрлiк векторы.
векторының бiрлiк векторы.
 және
және
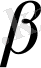 бұрыштары
бұрыштары
 векторының
векторының
 және
және
 өстерімен жасайтын бұрыш-
өстерімен жасайтын бұрыш-
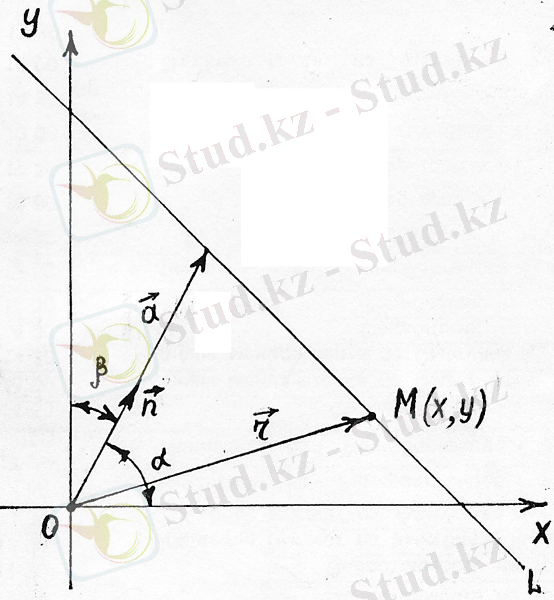
24-сурет
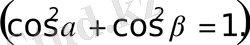 .
.
 нүктесi
нүктесi
 түзудiң кез келген нүктесi, оның радиус векторын
түзудiң кез келген нүктесi, оның радиус векторын
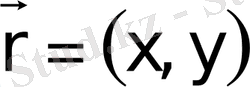 деп белгiлеймiз.
деп белгiлеймiз.
 түзудiң кез келген нүктесiнiң радиус векторының
түзудiң кез келген нүктесiнiң радиус векторының
 бiрлiк вектор бағытындағы проекциясы тұрақты және ол
бiрлiк вектор бағытындағы проекциясы тұрақты және ол
 -ға тең. Сонымен
-ға тең. Сонымен
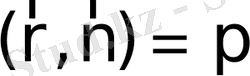
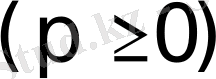

 теңдеу жазықтықтағы
теңдеу жазықтықтағы
 түзудiң
векторлық теңдеуi
деп аталады. Бұл теңдеу координаттар арқылы былай жазылады
түзудiң
векторлық теңдеуi
деп аталады. Бұл теңдеу координаттар арқылы былай жазылады
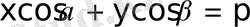
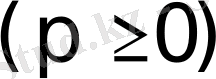
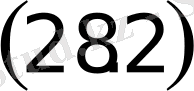
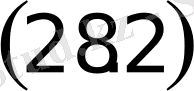 теңдеудi жазықтықтағы
теңдеудi жазықтықтағы
 түзудiң
нормаль түріндегі
теңдеуі
деп ата-лады. Бұл теңдеудiң екi жағын нөлден өзге кез келген санға көбейтсек нәти-жесінде
түзудiң
нормаль түріндегі
теңдеуі
деп ата-лады. Бұл теңдеудiң екi жағын нөлден өзге кез келген санға көбейтсек нәти-жесінде
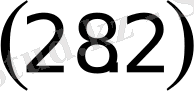 теңдеуге эквивалентті
теңдеуге эквивалентті
 түзудiң теңдеуін аламыз. Сонымен
түзудiң теңдеуін аламыз. Сонымен
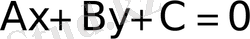

 теңдеу жазықтықтағы түзудiң
жалпы түрдегі теңдеуі
деп аталады. Бұл теңдеудi әрқашанда нормальді түрге келтіруге болады оны мына санға көбей-тiп
теңдеу жазықтықтағы түзудiң
жалпы түрдегі теңдеуі
деп аталады. Бұл теңдеудi әрқашанда нормальді түрге келтіруге болады оны мына санға көбей-тiп
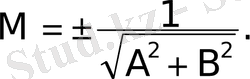

 саны нормалаушы көбейткiш деп аталады.
саны нормалаушы көбейткiш деп аталады.
 -ың таңбасы
-ың таңбасы
 санының таңбасына қарама-қарсы, себебі
санының таңбасына қарама-қарсы, себебі
 оң сан болуы керек.
оң сан болуы керек.
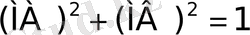 . 3 болғандықтан
. 3 болғандықтан
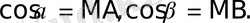 Equation. 3 Олай болса
Equation. 3 Олай болса
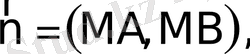 Equation. 3 ал
Equation. 3 ал
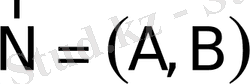 Equation. 3 векторы
Equation. 3 векторы
 түзуiне перпендикуляр, себебi ол
түзуiне перпендикуляр, себебi ол
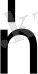 векторына коллинеарлы, шынында да
векторына коллинеарлы, шынында да
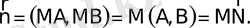 Сондықтан
Сондықтан
 векторын
векторын
 түзудiң нормалi деп атайды. Өздерiң көрiп отырғандай жазықтықтағы түзудiң тең-деулерiн кеңiстiктегi жазықтықтың теңдеулерiнiң дербес түрi деп қарас-тыруға болады. Сондықтан кеңiстiктегi жазықтықтың теңдеулерiнен жасал-ған барлық тұжырым жазықтықтағы түзулердiң теңдеулерiне де дұрыс.
түзудiң нормалi деп атайды. Өздерiң көрiп отырғандай жазықтықтағы түзудiң тең-деулерiн кеңiстiктегi жазықтықтың теңдеулерiнiң дербес түрi деп қарас-тыруға болады. Сондықтан кеңiстiктегi жазықтықтың теңдеулерiнен жасал-ған барлық тұжырым жазықтықтағы түзулердiң теңдеулерiне де дұрыс.
Түзудiң жалпы теңдеуiнiң дербес түрлерi:
- Егерболса, ондаEquation. 3 теңдеуi мына түрге келедiEquation. 3 БұлEquation. 3 өсiне параллель түзудiң теңдеуi;
- ЕгерEquation. 3 болса, ондаEquation. 3 түзуiөсiне параллель;
- Егерболса, ондаEquation. 3 теңдеуi бас нүктеEquation. 3 арқылы өте-тiн түзудiң теңдеуi.
 Equation. 3 теңдеудi мына түрге келтiруге болады, егер
Equation. 3 теңдеудi мына түрге келтiруге болады, егер
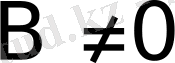 Equation. 3,
Equation. 3,

мұндағы
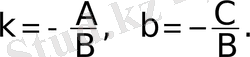
 теңдеудi мектептен белгiлi түзудiң
бұрыштық теңдеуi
деп аталады. Мұндағы
теңдеудi мектептен белгiлi түзудiң
бұрыштық теңдеуi
деп аталады. Мұндағы
 бұрыштық коэффициент, ал
бұрыштық коэффициент, ал

 тү-зуi мен
тү-зуi мен
 өсiнiң оң бағытының арасындағы бұрыш.
өсiнiң оң бағытының арасындағы бұрыш.
 нөлге тең болмаса
нөлге тең болмаса
 теңдеудi мына түрде жазуға болады
теңдеудi мына түрде жазуға болады
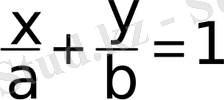
Мұндағы
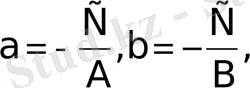
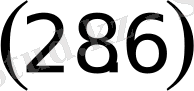 теңдеу түзудiң
кесiндiдегi теңдеуi
деп аталады. Бұл түзу
теңдеу түзудiң
кесiндiдегi теңдеуi
деп аталады. Бұл түзу
 өсiн
өсiн
 нүктесiнде,
нүктесiнде,
 өсiн
өсiн
 нүктеде қиып өтедi.
нүктеде қиып өтедi.
Екi түзудi қарастырайық
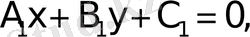
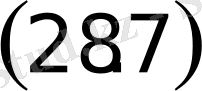
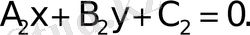
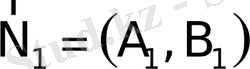 Equation. 3,
Equation. 3,
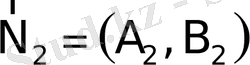 Equation. 3 векторлар осы екi түзудiң сәйкес нормаль векторлары. Екi түзудiң арасындағы бұрыш осы екi
Equation. 3 векторлар осы екi түзудiң сәйкес нормаль векторлары. Екi түзудiң арасындағы бұрыш осы екi
 Equation. 3 және
Equation. 3 және
 Equation. 3 векторлардың арасындағы бұрышқа тең. Скалярлық көбейтiндiнiң бiрiншi анықтамасынан
Equation. 3 векторлардың арасындағы бұрышқа тең. Скалярлық көбейтiндiнiң бiрiншi анықтамасынан
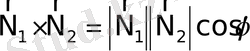 осыдан
осыдан
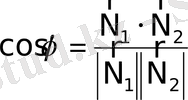 ,
,
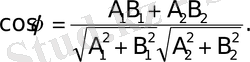
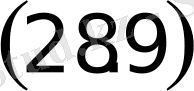
Егер
 Equation. 3 және
Equation. 3 және
 Equation. 3 перпендикуляр болса, онда олардың нормальдары да перпендикуляр болады, яғни
Equation. 3 перпендикуляр болса, онда олардың нормальдары да перпендикуляр болады, яғни
 осыдан
осыдан
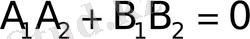

 теңдiк екi түзудiң перпендикуляр болу шарты. Егер
теңдiк екi түзудiң перпендикуляр болу шарты. Егер
 параллель болса, онда
параллель болса, онда
 және
және
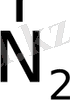 коллинеарлы векторлар, яғни
коллинеарлы векторлар, яғни
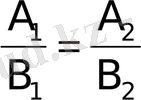

 теңдiк екi түзудiң параллель болу шарты.
теңдiк екi түзудiң параллель болу шарты.
 Equation. 3 және
Equation. 3 және
 түзулер бұрыш-тық теңдеулер арқылы берiлсiн, яғни
түзулер бұрыш-тық теңдеулер арқылы берiлсiн, яғни
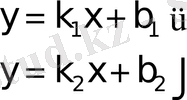

Онда
 жалпы түрге келтiрiп былай жазуға болады
жалпы түрге келтiрiп былай жазуға болады
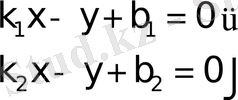

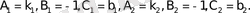
Екi түзудiң перпендикуляр болу шарты
 мынандай болады
мынандай болады
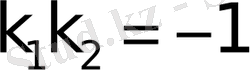

Екi түзудiң параллель болу шарты
 былай жазылады
былай жазылады
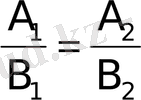 осыдан
осыдан
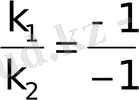 немесе
немесе
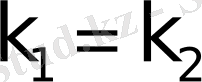

 пен
пен
 шарттар бұрыннан белгiлi.
шарттар бұрыннан белгiлi.
Егер
 түзу
түзу
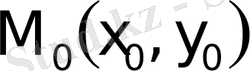 нүктесi арқылы өтсе, онда
нүктесi арқылы өтсе, онда
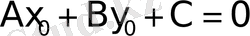

теңдiгi дұрыс.
 теңдiктен
теңдiктен
 -i алып мына теңдiктi аламыз
-i алып мына теңдiктi аламыз
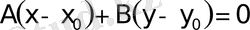

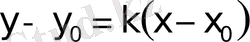

мұндағы
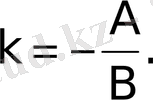
 және
және
 теңдеулердi түзудiң
бiр нүкте арқылы
теңдеулердi түзудiң
бiр нүкте арқылы
өтетiн
теңдеулерi деп аталады. Екi
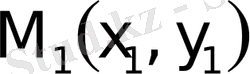 және
және
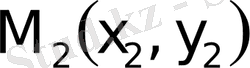 нүкте арқылы өтетiн түзудiң теңдеуi де осылайша анықталады
нүкте арқылы өтетiн түзудiң теңдеуi де осылайша анықталады
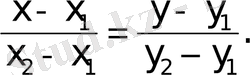

нүктеден жазықтықтағы түзуге дейiнгi ара қашықтықта нүктеде жазықтық-
тың ара қашықтықтың дербес түрi ретiнде қорытылады, сонымен
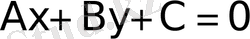 түзуiмен
түзуiмен
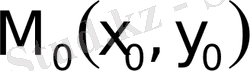 нүктенiң ара қашықтығы
нүктенiң ара қашықтығы
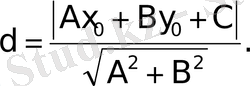

Мысал.
 нүктеден
нүктеден
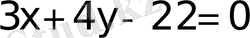 түзуге дейiнгi ара қашықтықты табу керек.
түзуге дейiнгi ара қашықтықты табу керек.
Шешiмi.
 формула бойынша
формула бойынша
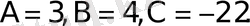

Олай болса
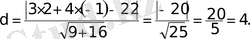
№5 дәрiс.
§29. Екiншi реттi қисық сызықтар
Дәрежелерi екiншi реттi болатын теңдеулермен анықталатын сызықтарды қарастырайық
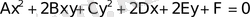
Бұл теңдеудiң коэффициенттерi нақты сандар және ең кем дегенде
 немесе
немесе
 -ның бiреуi нөлге тең емес. Мұндай сызықтарды
екiншi реттi сызықтар
(
қисықтар)
деп атайды.
-ның бiреуi нөлге тең емес. Мұндай сызықтарды
екiншi реттi сызықтар
(
қисықтар)
деп атайды.
Канондық теңдеулермен берiлген кейбiр қисықтарды қарастырайық.
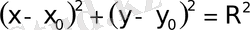
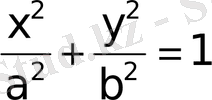
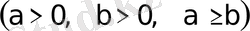
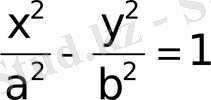
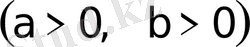
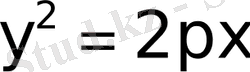
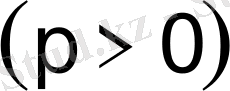
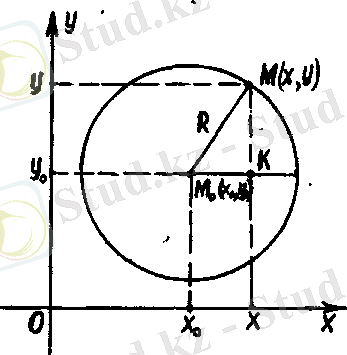
1. Шеңбер.
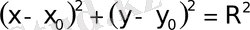 шеңбердiң канондық теңдеуi.
шеңбердiң канондық теңдеуi.
 нүктеден бiрдей
нүктеден бiрдей
 қашық-тықтағы нүктелердiң геометриялық орнын радиусы
қашық-тықтағы нүктелердiң геометриялық орнын радиусы
 -ге тең центрi
-ге тең центрi
 нүктеде жататын
шеңбер
деп атайды. Шеңбердiң канондық тең-деуiн 25-суреттен табамыз.
нүктеде жататын
шеңбер
деп атайды. Шеңбердiң канондық тең-деуiн 25-суреттен табамыз.
 -дан
-дан

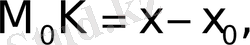

 онда
онда
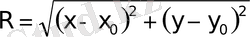 осыдан
осыдан
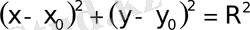
25-сурет
Егер
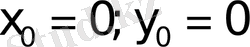 болса, онда центрi бас нүкте болатын шеңбердiң теңдеуi
болса, онда центрi бас нүкте болатын шеңбердiң теңдеуi
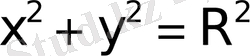
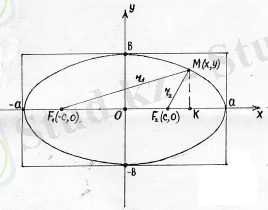
2. Эллипс.
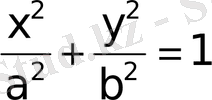
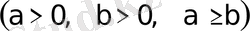
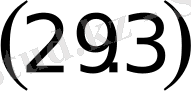 эллипстiң канондық теңдеуi.
эллипстiң канондық теңдеуi.
Эллипстiң канондық теңдеуi
 және
және
 -тiң тек жұп дәрежесiнен тұратын болғандықтан, егер
-тiң тек жұп дәрежесiнен тұратын болғандықтан, егер
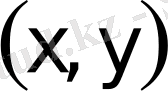 нүктесi осы эллипстiң нүктесi болса, онда
нүктесi осы эллипстiң нүктесi болса, онда
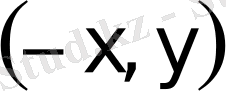 ,
,
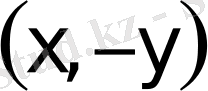 ,
,
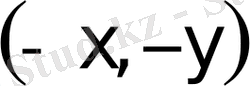 нүктелерi де осы осы эллипстiң нүктелерi болады. Сондықтан эллипс
нүктелерi де осы осы эллипстiң нүктелерi болады. Сондықтан эллипс
 және
және
 өстерiне симметриялы болады, сонымен қатар эллипс бас нүктеге де
өстерiне симметриялы болады, сонымен қатар эллипс бас нүктеге де
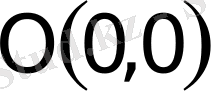 -де симметриялы.
-де симметриялы.
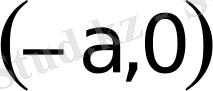 ,
,
 ,
,
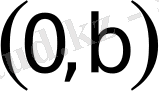 ,
,
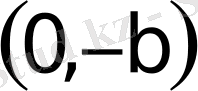 нүктелерi эллипстiң төбелерi,
нүктелерi эллипстiң төбелерi,
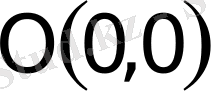 нүктесi эллипстiң центрi.
нүктесi эллипстiң центрi.
 - эл-
- эл-
липстiң үлкен жарты өсi,
 - кiшi жарты өсi деп аталады. Егер
- кiшi жарты өсi деп аталады. Егер
 болса, онда эллипс шеңберге айналады
болса, онда эллипс шеңберге айналады
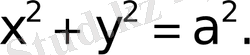
 теңдеудiң сол жағындағы әрбiр қосылғыш бiрден аспайды, яғни
теңдеудiң сол жағындағы әрбiр қосылғыш бiрден аспайды, яғни
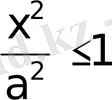 және
және
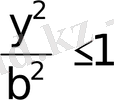 немесе
немесе
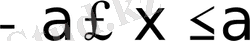 және
және
 Сондықтан эллипстiң барлық нүктелерi
Сондықтан эллипстiң барлық нүктелерi
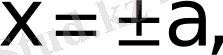
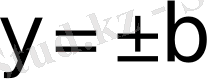 түзулерден тұратын төртбұрыш iшiнде жатады.
түзулерден тұратын төртбұрыш iшiнде жатады.
 26-сурет
26-сурет
 теңдеудегi терiс емес қосылғыштардың
теңдеудегi терiс емес қосылғыштардың
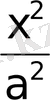 және
және
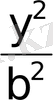 қосындысы бiрге тең. Сондықтан, егер бiр қосылғыш өссе екiншi қосылғыш кемидi, яғни
қосындысы бiрге тең. Сондықтан, егер бiр қосылғыш өссе екiншi қосылғыш кемидi, яғни
 өссе онда
өссе онда
 кемидi және керiсiнше. Сонымен эллипстiң графигi 26-суреттей болады.
кемидi және керiсiнше. Сонымен эллипстiң графигi 26-суреттей болады.
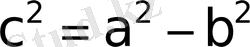 деп белгiлейiк.
деп белгiлейiк.
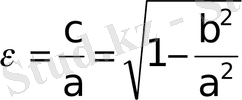 эллипстiң эксцентриситетi деп аталады.
эллипстiң эксцентриситетi деп аталады.
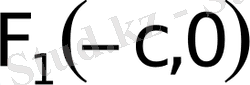 және
және
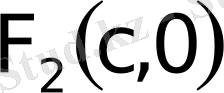 эллипстiң фокустерi, ал эллипстiң фокусiнен кез келген нүктесiне дейiнгi қашықтықтарды
эллипстiң фокустерi, ал эллипстiң фокусiнен кез келген нүктесiне дейiнгi қашықтықтарды
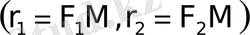
 нүктесiнiң фокальдық радиустерi деп атайды.
нүктесiнiң фокальдық радиустерi деп атайды.
Анықтама.
Фокустар деп аталатын екi
 және
және
 нүктеден ара қашық-тықтарының қосындысы тұрақты,
нүктеден ара қашық-тықтарының қосындысы тұрақты,
 болатын, жазықтықтағы нүктелердiң геометриялық орнын
эллипс
дейдi, яғни
болатын, жазықтықтағы нүктелердiң геометриялық орнын
эллипс
дейдi, яғни
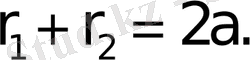
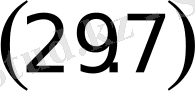
Эллипстiң канондық теңдеуiн осы
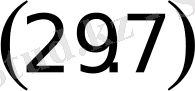 -ден қорытып шығаруға болады.
-ден қорытып шығаруға болады.
 эллипстiң кез келген нүктесi. 26-суреттегi
эллипстiң кез келген нүктесi. 26-суреттегi
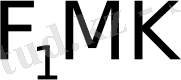 тiкбұрышты үшбұ-рыштан
тiкбұрышты үшбұ-рыштан
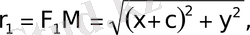 ал
ал
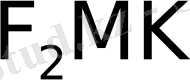 үшбұрыштан
үшбұрыштан
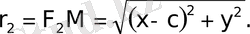
Бұл өрнектердi
 формулаға қойсақ мына өрнектi аламыз.
формулаға қойсақ мына өрнектi аламыз.
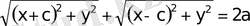 .
.
 формуланы былай түрлендiремiз
формуланы былай түрлендiремiз
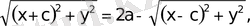 екi жағын квадраттап
екi жағын квадраттап
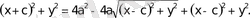 Осыдан
Осыдан
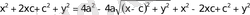 ,
,
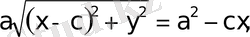 тағы
тағы
да екi жағын квадраттаймыз
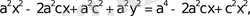
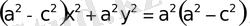
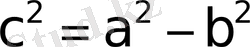 болғандықтан
болғандықтан
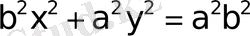 немесе
немесе
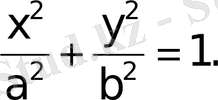
бұл теңдеу эллипстiң канондық теңдеуi.
3. Гипербола. Гиперболаның канондық теңдеуi
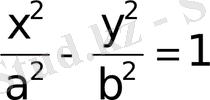
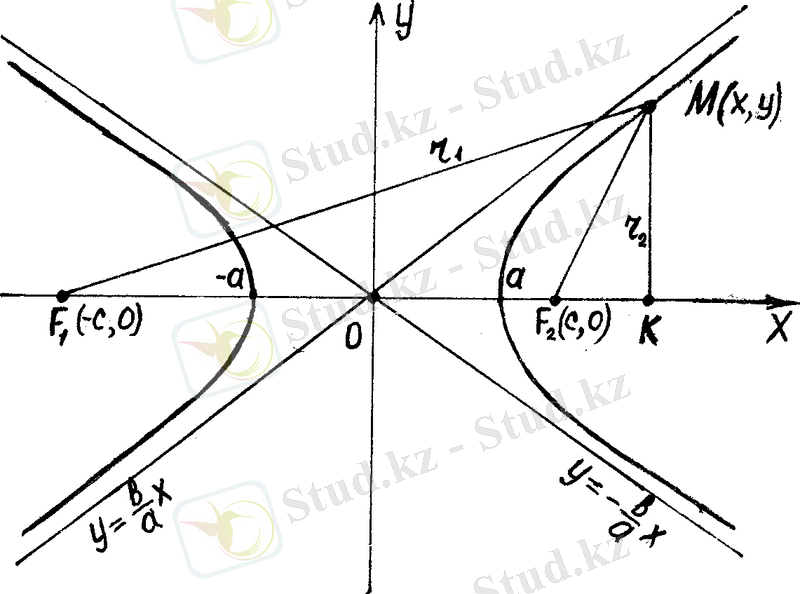
 теңдiкте
теңдiкте
 және
және
 -тiң дәреже-лерi жұп. Сондықтан гипербола
-тiң дәреже-лерi жұп. Сондықтан гипербола
 жә-не
жә-не
 өстерiне симметриялы, сонымен қатар гипербола
өстерiне симметриялы, сонымен қатар гипербола
 бас нүктеге де симметриялы.
бас нүктеге де симметриялы.
 өсiндегi
өсiндегi
 ,
,
 нүктелерi гиперболаның төбелерi деп,
нүктелерi гиперболаның төбелерi деп,
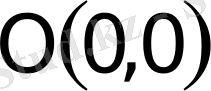 - гиперболаның центрi,
- гиперболаның центрi,
 өсi гиперболаның нақты өсi,
өсi гиперболаның нақты өсi,
 - жорамал өсi,
- жорамал өсi,
 - нақты жарты өсi,
- нақты жарты өсi,
 - жорамал жарты өсi деп аталады.
- жорамал жарты өсi деп аталады.
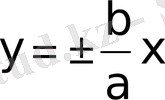 түзулерi гиперболаның көлбеу асимптоталары болатындығын дәлелдеуге болады.
түзулерi гиперболаның көлбеу асимптоталары болатындығын дәлелдеуге болады.
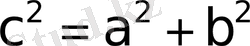 деп белгiлесек,
деп белгiлесек,
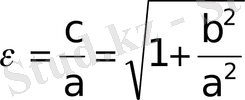 өрнектi гиперболаның эксцентриситетi деп атайды.
өрнектi гиперболаның эксцентриситетi деп атайды.
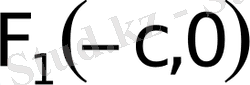 және
және
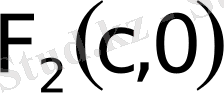 нүктелерi гиперболаның фокустерi,
нүктелерi гиперболаның фокустерi,
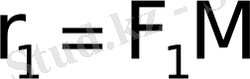 және
және
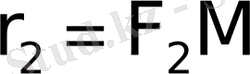 гиперболаның
гиперболаның
 нүктесiнiң фокальдық радиустерi деп аталады, мұндағы
нүктесiнiң фокальдық радиустерi деп аталады, мұндағы
 гиперболаның кез келген нүктесi (27-сурет) .
гиперболаның кез келген нүктесi (27-сурет) .
Анықтама.
Фокустар деп аталатын екi
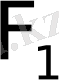 және
және
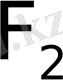 нүктеден ара қашықтықтарының айырымының абсолют шамасы тұрақты,
нүктеден ара қашықтықтарының айырымының абсолют шамасы тұрақты,
 болатын, жазықтықтағы нүктелердiң геометриялық орнын
гипербола
деп атайды, яғни
болатын, жазықтықтағы нүктелердiң геометриялық орнын
гипербола
деп атайды, яғни
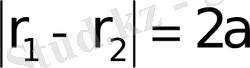
 формуланы пайдаланып 27-суреттен
формуланы пайдаланып 27-суреттен
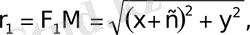
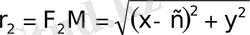 екендiгiн ескерiп гиперболаның канондық теңдеуiнiң
екендiгiн ескерiп гиперболаның канондық теңдеуiнiң
 -ке тең екендiгiн дәлелдеуге болады.
-ке тең екендiгiн дәлелдеуге болады.
- Парабола. Параболаның канондық теңдеуi
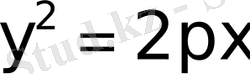
 Бұл теңдеудегi айнымалы
Бұл теңдеудегi айнымалы
 -тiң дәрежесi жұп, сондықтан парабола
-тiң дәрежесi жұп, сондықтан парабола
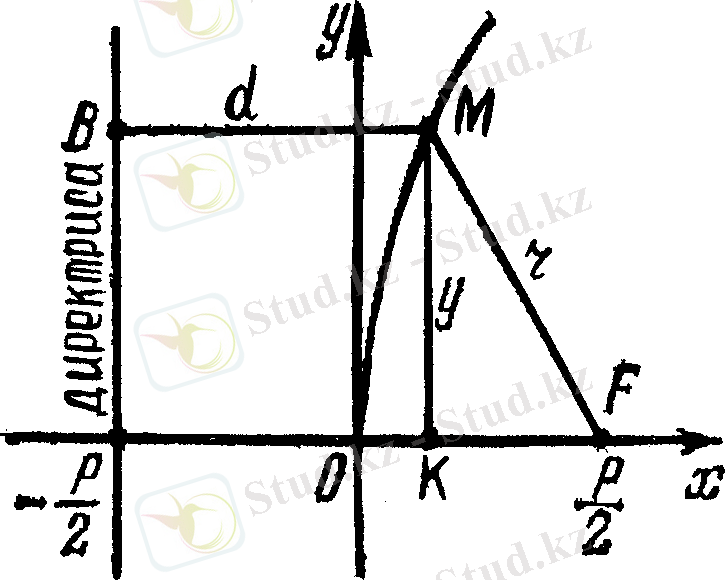
 өсiне сим-метриялы (28-сурет) .
өсiне сим-метриялы (28-сурет) .
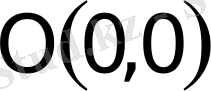 нүктесi пара-боланың төбесi,
нүктесi пара-боланың төбесi,
 нүктесi парабо-ланың фокусi,
нүктесi парабо-ланың фокусi,
 параболаның
параболаның
 нүктесiнiң фокальдық радиусi деп атала-ды, мұндағы
нүктесiнiң фокальдық радиусi деп атала-ды, мұндағы
 параболаның кез келген нүктесi (28-сурет) .
параболаның кез келген нүктесi (28-сурет) .
Анықтама.
 фокустен және директриса деп аталатын түзуден ара қашықтықтары бiрдей болатын нүктелердiң геометриялық орнын
парабола
деп атайды, яғни
фокустен және директриса деп аталатын түзуден ара қашықтықтары бiрдей болатын нүктелердiң геометриялық орнын
парабола
деп атайды, яғни


- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz