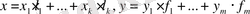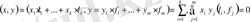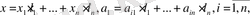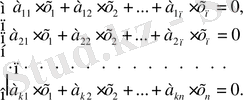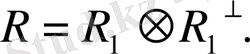Евклидтік кеңістіктегі ортогонал толықтауыштар және бірдей өлшемді евклидтік кеңістіктердің изоморфтығы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Ортогонал толықтауыш

Анықтама . Егер кез келген векторы кез келген векторына ортогонал болса, яғни (х, у) = 0, оyда евклид R кеңістігінің екі ішкі R ₁ , мсн R ₂ кеңістіктерін: 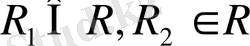өзара ортогонал деп атаймыз, яғни .

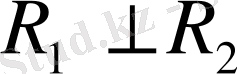Теорема. Евклид R кеңістігінің ішкі R ₁ , мсн R ₂ кеңістіктегі бір-бірімен ортогонал болу үшін, 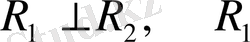яғни кеңістігінің барлық базистері R ₂ кеңістігінің барлық базистеріне ортогонал болуы қажетті әрі жеткілікті.

Қажеттілігі. R ₁ , мсн R ₂ кеңістіктері өзара ортогонал болсын деп ұйғарайық, яғни 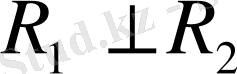. Онда анықтама бойынша, R ₁ кеңістігінің барлық базистері R ₂ кеністігінің барлық базистерінс ортогонал болады.

Жеткіліктілігі. 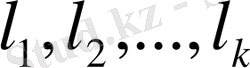векторлар жүйесі, R ₁ кеңістігінің базисі, ал 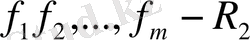кеңістгінің базисі болсын және 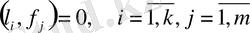тендіктсрі орындалсын деп есептелік. Енді кез келген

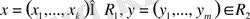
векторлардың сәйкес базистердс жіктеулерін

алып, олардык скаляр көбейтіндісін қарастыралық. Онда

ягни кез келген векторлары ортогонал немесе 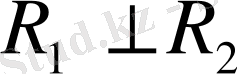Теорсма дәлелденді.

Теорема. Егер евклид R кеңістігінің екі ішкі R ₁ , мсн R ₂ кеңістіктері өзара ортогонал болса: 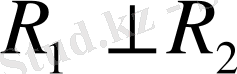онда олардың қиылысуы нол вектор болады; .

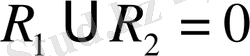
Дәлелдеуі. Кез келген х вектор 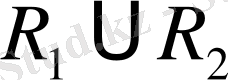кеңістігінің элементі болсын деп ұйғаралық, яғни . Онда және ( х, х ) = 0. Бұдан х = 0. Теорема дәлелденді.

Айталық, евклид R кеңістігінің кезкелген ішкі R ₁ , кеңістігі берілсін: 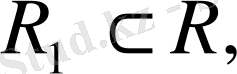ал 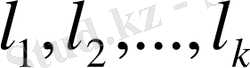оның ортонормалданған базисі болсын делік. Енді ол базисті евклид R кеңістігінің ортонормалданған базисіне дейін толықтыралық, яғни 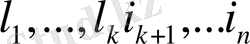мұндағы 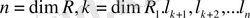векторлар жүйесі евклид R кеңістігінің өлшемі (n - k) -ға тең ішкі R ₂ кеңістігін құрастырады, яғни

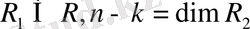
Теорема . Егер кез келген всктор ішкі R ₁ кеңістігінің кез келген векторына ортогонал болса: 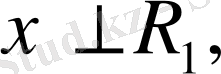онда х ішкі R ₂ кеңістігінің векторы:

Д әл е л д е у і. Теореманың шарты бойынша 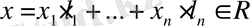және 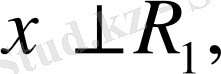яғни

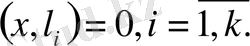
Енді х вектордың жіктелуінің екі жағында 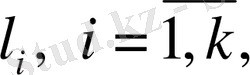векторларына біртіндеп скаляр көбейтелік:

Егер 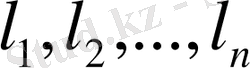ортонормалданған векторлар және (x, l _i ) =0 екенін ескерсек, онда

(x, l _i ) =x _i =0,

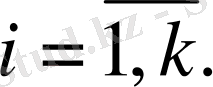
Демек, x вектордың жіктелуі мына түрде жазылады: 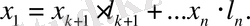Бұдан, Теорема дәлелденді.

Анықтама. Егер векторлар жиыны ішкі R ₁ кеңістігінің кез келген векторына ортогонал болса, онда ондай векторлар жиынын 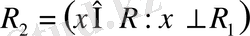ішкі R ₁ кеңістігінің ортогонал толықтауышы деп атаймыз, ал ол ішкі R ₂ кеңістікті 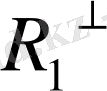символымен белгілейміз 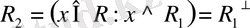мұндағы 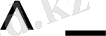перпендикуляр таңбасы.

Теорема. Егер 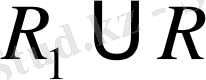және 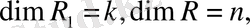онда 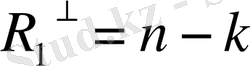немесе .

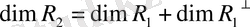Дәлелдеуі. a ₁ , a ₂ …, a _k векторлар жиыны ішкі R ₁ кеңістігінің базисі, ал a _i1 , a _i2 …, a _1n нақты сандар жиыны а вектордың координаттары болсын деп ұйғаралық:

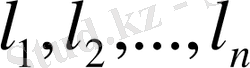векторлар жиыны евклид R кеңістігінің ортонормалданған базисі болсын. Онда:

мұндағы х ₁ , . . . , х _n берілген вектордын координаттары.

Берілген вектор х = (x ₁ . . . , х _n ) ішкі 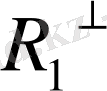кеңістігінің элементі болу үшін, яғни ,

(x, a _i ) =x _i =0,

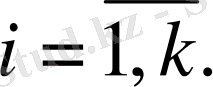
теңдіктердің орындалуы қажетті әрі жеткілікті. Енді формулаларды тендіктерге қойып, және 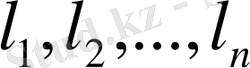ортонормалданған векторлар екенін ескерсек, онда

мұндағы х ₁ , х ₂ . . . , х _n вектор х-тің координаттары. Бұл біртекті сызықты теңдеулер жүйенің матрицасының рангісі k. Сондықтан, жүйенің (п - k) сызықты тәуелсіз шешімі бар. Олай болса, 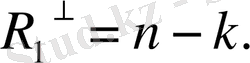Теорема дәлелденді.

теоремаларды сскеріп, мына төмендсгі тұжырымға кслсміз.

6-теорема. Евклид R кеңістігі өзінің кез келген ішкі R ₁ кеңістігімен оның 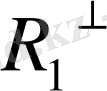ортогонал толықтауышының тура қосындысына тең:

Евклид кеңістіктерінің изоморфтылығы.

Анықтама. Егер екі евклид R мен кеңістіктерінің элементтері (векторлары) арасында бір мәнді сәйксетік анықталып: 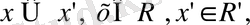төмендегі шарттар орындалса, онда олар изоморфты болады. Бұл жағдайда:

1) егер R кеңістігінің х, у элементтеріне кеңістігінің x', у' элементтері сәйкес келсе 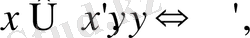онда 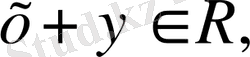элементіне 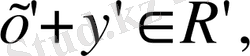элементі сәйкес келеді,

2) егер 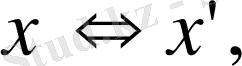онда мұндапд а - кез келген нақты сан.

3) егер 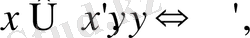онда (х, у) = (х', у') .

Сонымен, олар сызықты кеңістіктер ретіндс изоморфты болса және олардың екі сәйкес элементтерінің (векторларының) скаляр көбейтінділері өзара тең болса, онда екі Евклид R мен кеңістіктері изоморфты болады.