Орта мектепте теңдеулер мен теңсіздіктерді шешуде жаңа технологиялық әдістерді қолдану


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Ы. АЛТЫНСАРИН АТЫНДАҒЫ АРҚАЛЫҚ МЕМЛЕКЕТТІК
ПЕДАГОГИКАЛЫҚ ИНСТИТУТЫ
ЖАРАТЫЛЫСТАНУ ЖӘНЕ АҚПАРАТТАНДЫРУ ФАКУЛЬТЕТІ
МАТЕМАТИКА, ФИЗИКА ЖӘНЕ ИНФОРМАТИКА
КАФЕДРАСЫ
ДИПЛОМДЫҚ ЖҰМЫС
ОРТА МЕКТЕПТЕ ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУДЕ ЖАҢА ТЕХНОЛОГИЯ ӘДІСІН ПАЙДАЛАНУ
Орындаған: 050109 «Математика» мамандығының
IV курс студенті Келденбек Досбол
Ғылыми жетекшісі:
Аға оқытушы Еденов А. Е.
Арқалық 2009
МАЗМҰНЫ
КІРІСПЕ
І. НЕГІЗГІ БӨЛІМ . . . 3
1. ОРТА МЕКТЕП МАТЕМАТИКАСЫНДАҒЫ ТЕҢДЕУЛЕР
МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУ
1. 1 Бір айнымалысы бар теңдеулер . . . 6
1. 2 Квадрат теңдеулер . . . 9
1. 3 Екі айнымалысы бар теңдеулер . . . 12
1. 4 Иррационал теңдеулер мен теңсіздіктер . . . 18
1. 5 Үшінші және төртінші дәрежелі теңдеулерді шешу . . . 20
1. 6 Логарифмдік теңдеулер мен теңсіздіктерді шешу . . . 26
1. 7 Орта мектеп бағдарламасында теңсіздіктердің қасиеттері
және оларды дәлелдеу . . . 29
ІІ. ПРАКТИКАЛЫҚ БӨЛІМ.
2. МАТЕМАТИКАНЫ ОРТА ЖӘНЕ ЖОҒАРЫ МЕКТЕПТЕ
ОҚЫТУДЫҢ ЖАҢА ТЕХНОЛОГИЯ ӘДІСТЕРІ . . . 33
2. 1 Деңгейлеп оқыту технологиясын математика пәніндегі
теңдеулер мен теңсіздіктерде қолданудың тиімділігі . . . 36
2. 2 Математиканы оқытудың эврестикалық және программаланған
әдістерін теңдеулер мен теңсіздіктерді шешуде пайдалану . . . 40
2. 3 Мектепте математика пәнін оқытудағы жаңа технологиялық
ақпараттық-коммуникациялық технологияларды қолданудың
тиімділігі . . . 45
2. 4 Саралап оқыту әдісі (Ж. А. Қараевтың деңгейлеп саралап
оқыту технологиясы) . . . 48
2. 5 Модульдік оқыту әдісі . . . 51
2. 6 Математикалық теңдеулер мен теңсіздіктерді шешу және сабақта кіріктіре
оқыту әдістемесі . . . 65
2. 7 Орта мектепте теңдеулер мен теңсіздіктерді шешудің жолдары мен әдіс-тәселдері . . . 67
ҚОРЫТЫНДЫ . . . 73
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР . . .
КІРІСПЕ
Қазіргі таңда орта және жоғары оқу орындарында математиканы оқытудың мақсаты-оқырмандарға күнделікті өмірде және қазіргі қоғамда пайдалы еңбек еткенде қажет болатын және де басқа пәндерді оқып меңгеруге, білімін әрі қарай жалғастыруға толық мүмкіншілік беретін математикалық білім, іскерлік және дағдылардың негізін берік және саналы түрде меңгеріп алуын қамтамасыз ету.
Орта және жоғары мектепте білім беру және тәрбие жұмыстары жеке тұлғаның дамуына толық бағытталған деп айтуға негіз жоқ, әлі де біз дәстүрлі ақпараттық-түсіндірме тәсілі бойынша білім беруден шыға алмай келеміз. Сондықтан біздің алдағы уақыттағы негізгі мақсатымыз - оқушыларға жеке тұлға ретінде қарап, оларды жан-жақты дамыту, шығармашылық мүмкіндіктерін, іс-қабілетін арттыру керек, ол үшін оқу үрдісінің мазмұнының іске асырылу жолдарының логикасын қайта қарап, кәсіби дайындығын қазіргі заман талабына сәйкестендіру тез уақытта шешуді талап ететін мәселелердің бірі.
Орта мектепте теңдеулер мен теңсіздіктерге байланысты материалдар математиканың негізгі бөлігін құрайды, өйткені теңдеулер мен теңсіздіктер математиканың әр бөлімдерінде және маңызды қолданбалы есептерді шығаруда кең қолданыс табады. Осыған орай оқушыларды мектеп қабырғасында теңдеулер мен теңсіздіктер желісінің қолданбалық, теориялық-математикалық желілерімен байланысын құру бағыттарын игерту мәселесі теңдеулер мен теңсіздіктерді шешуге үйрету материалдарын талдау мен сапалы игерту мәселесімен тығыз байланыста.
Орта мектептерде теңдеулер мен теңсіздіктерді шешу әдістерін беру кезінде қойылатын іргелі мақсаттардың қатарына есептерді тиімді шешу дағдылары мен іскерліктерін дамыту проблемасы жатады. Мәселенің күрделігі мен қиындығынан осы уақытқа дейін ол түпкілікті ғылыми-әдістемелік шешімдерін таба алмай келеді. Осыған байланысты орта мектепте теңдеулер мен теңсіздіктерді шешуге тереңдетіп оқыту әдістемесін қолдануы, олардың теориялық білімдерін нақтылаудың, оларды практикада қолдана алу ептіліктерін қалыптастырудың басты формаларының бірі.
Математикада теңдеуді де, теңсіздікті де өмірде болған немесе болып жатқан құбылысты зерттеу құралы ретінде пайдаланады. Теңдеу арқылы процестің дәл шешімі зерттелсе, ал теңсіздік арқылы белгілі бір аралықтағы қозғалыс зерттеледі. Теңдеу мен теңсіздікті білім қалыптастырудың тиімділігі тұрғысынан қарастырғанда, келесі проблемаларды шешу керектігі шығады.
1. Құрылымы әр түрлі теңдеулердің шешімдерін табу әдістеріне үйреткеннен кейін теңсіздіктердің шешімдерін табуға үйрету;
2. Теңдеу мен теңсіздіктердің есептемелерін біріктіріп табуға үйрету.
Орта мектепте математиканы оқыту кезеңінде математикалық білімнің жүйелігі мен күнделігінің деңгейін бағалау үшін оқушылардың теңдеулер мен теңсіздіктерді шешудегі оқыту әдістерін еркін таңдай білуіне, іс-жүзінде қарапайым және қолайлы жағдайды математикалық модель түрінде қарастыру біліктілігіне, күрделі есептерді шешуде математикалық әдістерді қолдана алу деңгейлеріне сүйену керек. Математиканы оқытуда теңдеулер мен теңсіздіктерді шығаруды үйрету ғана емес, ол кез келген проблеманы шеше білуде, қиындықты жеңуде, танымдық және ойлау қабілеттерді жетілдіруде маңызды роль атқарады.
Орта мектеп бағдарламасында теңдеулер мен теңсіздіктерден бастап, жоғары дәрежелі теңдеулер мен теңсіздіктерді шешу теориясы мен практикалық мәселелеріне дейін кең орын берілген. Мысалы, сызықтық теңсіздіктерді шешу, екінші дәрежелі теңсіздіктер көмегімен квадраттық үшмүшені зерттеу, теңдеулер жөнінде талдау жасау, жуықтап есептеулер, иррационал саңдар теориясы, сандық қатарлар сияқты мәселелер теңсіздіктер арқылы түсіндіріледі. Теңдеулер мен теңсіздіктер теориясы орта мектепте оқушылардың логикалық ойлау қабілетін дамыта алатындай, өз алдына ғылыми-педагогикалық маңызы бар негізгі оқу материалы болып есептеледі. Сондықтан есеп шығару барысында творчестволық қабілеттілік, ізденгіштілік қасиеттерді әр түрлі тәсілдермен шығарып, ішінен ең қарапайым, тиімдісін таңдап алудың маңызы зор. Соңғы кезде орта мектеп математикасында көптеген жақсы бетбұрыстарға қарамастан теңсіздіктер жөнінде мектеп оқушыларының түсініктері мардымсыз. Осы олқылықты жою үшін теңсіздіктер теориясы мен оны үйренудің әдісін жетілдіру қажет.
Мысалы, алгебралық
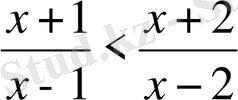 теңсіздігінде белгісіздің мәндері 1 мен 2-ден басқа сандар болуы керек. Бұл мәндерде бөлшектердің мағынасы жоқ болады. Сонымен теңсіздікті дәлелдегенде және шешкенде әріптер мен белгісіз шамалардың мүмкін мәндерін үнемі есепке алып отыру керек. Таңбасы белгісіздің мүмкін мәндерінің бәрінде де сақталатындай теңсіздік шартсыз теңсіздік деп аталады.
теңсіздігінде белгісіздің мәндері 1 мен 2-ден басқа сандар болуы керек. Бұл мәндерде бөлшектердің мағынасы жоқ болады. Сонымен теңсіздікті дәлелдегенде және шешкенде әріптер мен белгісіз шамалардың мүмкін мәндерін үнемі есепке алып отыру керек. Таңбасы белгісіздің мүмкін мәндерінің бәрінде де сақталатындай теңсіздік шартсыз теңсіздік деп аталады.
Барлық теңсіздіктердің қасиеттерін сандық теңсіздіктер арқылы көрсетуге болады. Енді сол теңсіздіктердің біраз қасиеттеріне тоқталып өтейік.
1.
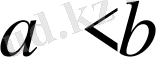 теңсіздігінен
теңсіздігінен
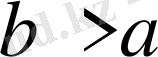 теңсіздігі шығады. Демек, теңсіздіктердің бөліктерін ауыстырғанда теңсіздік таңбасы да ауысады. Бұл қорытынды тікелей теңсіздіктердің анықтамасынан шығады.
теңсіздігі шығады. Демек, теңсіздіктердің бөліктерін ауыстырғанда теңсіздік таңбасы да ауысады. Бұл қорытынды тікелей теңсіздіктердің анықтамасынан шығады.
2.
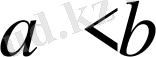 және
және
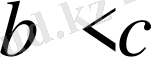 теңсіздіктерінен
теңсіздіктерінен
 теңсіздігі шығады. Берілген шарт бойынша
теңсіздігі шығады. Берілген шарт бойынша
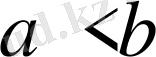 және
және
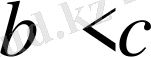 . Сондықтан
. Сондықтан
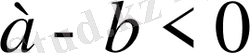 және
және
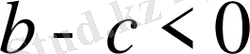 . Екі теріс санның қосындысы да теріс сан болатындықтан,
. Екі теріс санның қосындысы да теріс сан болатындықтан,
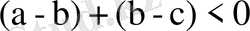 жақшаларын ашсақ,
жақшаларын ашсақ,
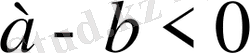 сонда
сонда
 . Бұл қасиет есептерді шешкенде, теоремаларды дәлелдегенде теңсіздікті күшейту үшін қолданылады.
. Бұл қасиет есептерді шешкенде, теоремаларды дәлелдегенде теңсіздікті күшейту үшін қолданылады.
Соңғы кезде орта мектептегі математиканың бағдарламасында теңсіздіктерді дәлелдеуге дұрыс көңіл бөлмей келеді.
Мектеп оқулықтарында бұл мәселеге арнап есептер құрастырылмаған.
Оқыту үрдісінде теңсіздіктерді шешекенде теңсіздік қасиеттерін қолдана білу дағдыларын барынша дамыту аса маңызды роль атқарады. Бұл болашақта мамандығы математикамен байланыста болатын студенттер үшін қажет. Себебі теңсіздіктердің қасиеттеріне сүйеніп теңсіздіктерді дәлелдеу әдістерін игере алу дағдысы жоғары математика курсын жақсы меңгеру үшін ерекше маңызды.
Математикалық білім беруді дамытудың стратегиялық бағытын және алдын-ала болжаудың біртұтас кешендік мәселелері айқындалып, оның қазіргі кезеңдегі математикалық мәдениетінің бір элементі ретіндегі орны мен мақсаттарын анықтау проблемаларын шешу қажет, яғни студенттердің меңгеру деңгейіне қажетті және тиімді мазмұн көлемін анықтайтын, қазіргі талапқа сәйкес математикалық білім негізін жете зерттеу мәселесі өзекті мәселенің бірі болып отыр. Сонымен жаңа технология бойынша жоғары мектептерде теңдеулер мен теңсіздіктерді шешудің әдістемесін жетілдіру, оқыту мазмұнының қолданбалық бағытын күшейту, алған білімдерін практикада қолдануға талпындыра отырып, оқыту процесінің әдіс-тәсілдерін қолданудың тиімді жолдарын кешенді түрде игерулеріне мүмкіндік береді.
Координаттық түзуді пайдалану кейбір теңсіздіктер мен бір белгісізі бар теңсіздік жүйесін және теңдеулер мен модульді теңсіздіктерді шешуге мүмкіндік береді. Мысалы, бір белгісізі бар сызықтық теңсіздіктерді шешуде алдымен координаталық түзуге теңсіздіктің көптеген шешімдері жүргізіледі, одан барып олардың жалпы бөлігі белгіленеді. Теңдеулер мен модульді теңсіздіктерді шешу сандардың түрлілік модульдеріне геометриялық түсінік берумен байланысты. Мысалы, теңдеудің шешімі
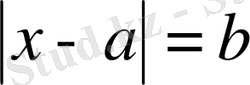 координаталық түзуге
координаталық түзуге
 координаталық нүктесінен
координаталық нүктесінен
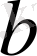 нүктесіне дейін қашықтаған нүктені табуға әкеледі.
нүктесіне дейін қашықтаған нүктені табуға әкеледі.
Мысал ретінде
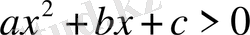 теңсіздігіне көрсетілген көптеген шешімдер келтірілген схемасын алуға болады. Оқушылар жаттығу барысында мұндай схеманы пайдалануға үйреніп, одан оны елестетіп пайдалануға үйренеді.
теңсіздігіне көрсетілген көптеген шешімдер келтірілген схемасын алуға болады. Оқушылар жаттығу барысында мұндай схеманы пайдалануға үйреніп, одан оны елестетіп пайдалануға үйренеді.
Тақырыптың өзектілігі:
Орта мектепте теңдеулер мен теңсіздіктерді шешуде жаңа технологиялық әдіс-тәсілдері арқылы оқыту.
Дипломдық жұмыстың мақсаты:
Еліміздің экономикасы артып, мектептердің техникалық базасы нығайып, арнайы компьютерлік техникалармен, оқытудың модульдік, деңгейлік, саралап, ақпараттық-коммуникативтік, эврестикалық және программаланған технологиялары арқылы оқыту.
Дипломдық жұмыстың міндеті:
- Жалпы әлеуметтік пәндік және пән аралық біліктіліктіі игеруді қалыптасытру, яғни алынған білімді қолдану тәсілдерін меңгерту;
- Оқушылардың тиімділігін жоғарылатады және оқыту материалын түсіндіру мүмкіндігін меңгерту;
- Мұғалімдердің инновациялық және ақпараттық технолгияларды қолдануы;
- Сабақ уақытын тиімді пайдалану;
- Мұғалім мен оқушылардың еңбегін ғылыми тұрғыда ұйымдастыру;
- Оқушыларды бағалауда уақытты тиімді пайдалану.
1. ОРТА МЕКТЕП МАТЕМАТИКАСЫНДАҒЫ
ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУ
1. 1 Бір айнымалысы бар теңдеулер
Анықтама: f(х), g(х) айнымалысы х болатын өрнек және анықталу обылысы Х болсын. Сонда g(х) түріндегі теңдік, пікірлік форма бар х айнымалы теңдеу деп аталады. f(х) пен g(х) өрнектері тең сандық мән қабылдайтындай айнымалының әрбір мәні теңдеудің түбірлері деп аталады. Теңдеуді шешу дегеніміз оның барлық түбірлерін табу немесе оның түбірлері жоқ екенін дәлелдеу.
3 х+х= 40 теңдеуінің бір түбірі бар. Екі, үш және оданда көп түбірлері болатын немесе жалпы алғанда түбірлері болмайтын теңдеулерді мысалға келтіруге болады.
Мысалы, ( х -4) ( х -5) ( х -6) =0 теңдеуінің үш түбірі бар, олар: 4, 5, және 6. Шындығында, осы сандардың әрқайсы ( х -4) ( х -5) ( х -6) өрнегінің әрбір көбейткішін нөльге айналдырады, олай болса, көбейтіндінің өзін де нөльге айналдырады. х -тің басқа кез келген мәнінде көбейткіштердің бірде біреуі нольге айналмайды, олай болса, көбейтінді де нөльге айналмайды. х +2= х теңдеуінің түбірлері болмайды, өйткені кез келген х мәнінде теңдеудің сол бөлігін оң бөлігінен 2-ге артық болады.
х 2 =4 теңдеуінің екі түбірі бар: 2 және -2 сандары, ( х -2) ·( х +2) =0 теңдеулерінің түбірлері де 2 және -2 сандары. Бұндай бірдей түбірлері бар теңдеулерді мәндес теңдеулер деп атайды. Түбірлері болмайтын теңдеулер де мәндес теңдеулер деп есептеледі.
Теңдеулердің мынандай қасиеттері болады:
1) егер теңдеудің екі бөлігіне де бірдей санды қосса, онда берілген теңдеумен мәндес теңдеу шығады;
2) егер теңдеудің екі бөлігін де нөльге тең емес бірдей санға көбейтсе немесе бөлсе, онда берілген теңдеумен мәндес теңдеу шығады.
х 2 -2=7 теңдеуін қарастырайық. Осы теңдеудің сол бөлігіне де, оң бөлігіне де 2 санын қосып, х 2 =9 теңдеуінің мәндес болатынын дәлелдейік. х -тің қайсыбір мәні бірінші теңдеудің түбірі дейік, яғни х -тің осы мәнінде х 2 -2=7 теңдеуі тура теңдікке айналады. Осы теңдіктің екі бөлігіне де 2 санын қосып, біз қайтадан тура теңдік шығарып аламыз. Олай болса, х -тің осы мәнінде екінші теңдеу де тура теңдікке айналады. Біз бірінші теңдеудің әр түбірі екінші теңдеудің де түбірі болып табылатынын дәлелдедік.
Енді х -тің қайсыбір мәні екінші теңдеудің х 2 =9 түбір болсын, яғни оны тура теңдікке айналдырады дейік. Осы теңдіктің екі бөлігінен де 2 санын шегеріп, біз тура теңдік шығарып аламыз. Олай болса, х -тің осы мәнінде бірінші теңдеу де тура теңдікке айналады. Сондықтан екінші теңдеудің әр түбірі бірінші теңдеудің де түбірі болып табылады.
Сонымен, х 2 -2=7 және х 2 =9 теңдеулерінің түбірлері бірдей, яғни олар мәндес теңдеулер болып табылады.
Осы сияқты баяндай келе, теңдеулердің екі қасиетінің де жалпы жағыдайда дұрыстығы шығады.
Егер қосылғыштың таңбасын өзгертіп, теңдеудің бір бөлігінен оның екінші бөлігіне көшірсе, онда берілген теңдеумен мәндес теңдеу шығады. Бұл анықтаманы дәлелдеп көрейік. Мысалы, 5 х =2 х +9 теңдеуінде қосылғыш 2 х -ті қарама-қарсы таңбасымен теңдеудің оң бөлігінен сол бөлігіне көшіріп те, сол теңдеумен мәндес 5 х -2 х =9 теңдеуін шығарып аламыз.
Теңдеуді шешкенде қосылғыштарды теңдеудің бір бөлігінен екінші бөлігіне көшіру жиі пайдаланылады.
Анықтама.
aх=b
(мұндағы
х
-айнымалы,
а
және
b
- сандар) түріндегі теңдеуі бір айнымалысы бар сызықтық теңдеу деп аталады.
а
санын айнымалының жанындағы коэффицент, ал
b
санын босмүше деп атайды.
aх=b
сызықты теңдеуді қарастырайық, мүның
а
коэффициенті нольге тең емес. Теңдеудің екі бөлігін де
а
-ға бөліп,
х
=
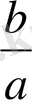 теңдігін шығарып аламыз. Демек,
ах=b (a≠0)
сызықты теңдеудің бір ғанам
теңдігін шығарып аламыз. Демек,
ах=b (a≠0)
сызықты теңдеудің бір ғанам
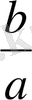 түбірі болады. Енді
ах=b
сызықты теңдеуді қарастырайық, мұның
а
коэффиценті нольге тең. Егер
а=0
және
b≠0
болса, онда
ах=b
теңдеуінің түбірлері болмайды, өйткені
0х=b
теңдігі (
b
≠0)
х
-тің ешбір мәнінде тура мән болмайды. Егер
а=0
және
b≠0
болса,
х
-тің кез келген мәні теңдеудің түбірі болады, ойткені
0х=0
теңдігі кез келген
х
мәнінде тура. Көптеген теңдеулердің шешу жолы сызықтық теңдеулерді шешуге келіп тіреледі.
түбірі болады. Енді
ах=b
сызықты теңдеуді қарастырайық, мұның
а
коэффиценті нольге тең. Егер
а=0
және
b≠0
болса, онда
ах=b
теңдеуінің түбірлері болмайды, өйткені
0х=b
теңдігі (
b
≠0)
х
-тің ешбір мәнінде тура мән болмайды. Егер
а=0
және
b≠0
болса,
х
-тің кез келген мәні теңдеудің түбірі болады, ойткені
0х=0
теңдігі кез келген
х
мәнінде тура. Көптеген теңдеулердің шешу жолы сызықтық теңдеулерді шешуге келіп тіреледі.
Теңдеулерді шеше келе, 0х=b түріндегі сызықтық теңдеуге келіп тірелуі мүнкін. Бұндай жағыдайда бастапқы теңдеудің түбірі болады не болмайды, не кез келген сан оның түбірі бола береді. Мысалы, 2 х +5=( х +6) теңдеуі 0 х =7 теңдеуіне келеді, олай болса, бұл теңдеудің түбірі болмайды, 3( х +2) + х =6+4 х теңдеуі 0 х -0 теңдеуіне келеді, олай болса, кез келген сан оның түбірі болып табылады.
1. Бір белгісізі бар теңдеуді шешкенде оқушыларға көңіл бөлетін нәрсе, ол таңбаларына жақсы қарау керек.
а ) алдында «+», «-» таңбасы бар жақшаларды ашу кезінде қосылғыштардың таңбаларынан,
ә ) көбейтудің қосуға немесе азайтуға қатысты үлестірімділік заңын қолданудан,
б ) белгісіз мүшелерді теңдеудің бір жағына, бос мүшелерді теңдеудің екінші жағына жинақтау кезінде таңбалардан қателер жібереді. Сондықтан осындай қателерді болдырмау үшін оқушыларға тақырыпты былайша түсіндірген жөн. Алдымен теңдеулер және олардың қасиетіне сүйеніп, мынандай түрлендірулер жасауға болатынын оқушыларға жеткізу керек.
1-мысалы: х -4=7 мәндес теңдеудің бірінші қасыйетіне сүйеніп теңдеудің екі жағын да 4-ті қосайық. Сонда х -4+4=7+4; х =7+4 х =11:
2-мысал: 3 х =2 х -5 екі жағын да -2 х- ті қосайық. Сонда 3 х +(-2 х ) =2 х +(-2 х -5) ; 3 х -2 х =-5; х =5: Осы мысалдар арқылы мынандай қортындыға келеміз:
а ) Берілген теңдеулердің кейбір мүшелерін теңдеудің бір жағынынан екінші жағына қарама-қарсы таңбамен көшіруге болады.
б ) Теңдеуді шешкендне белгісізі бар мүшелер теңдік таңбасның бір жағына, бос мүшелер теңдік таңбасының екінші жағына жинақталады. Осы екі қортындыға сүйеніп теңдеуді шешудің алгоритмін оқушыларға жаздырамыз.
1. Теңдеудегі белгісіздерді теңдеудің бір жағына, әдетте сол жағына жинақтау керек. ол үшін сол жақта белгісіздер болса, таңбасын өзгерпей жазып алып, оң жақта тұрған белгісіздерді алдындағы таңбасын қарама-қарсы таңбаға өзгертіп сол жаққа көшіру керек.
2. Бос мүшелерді теңдеудің бір жағына әдетте оң жағына жинақтау керек. Ол үшін оң жақта бос мүше болса, таңбасын өзгертпей жазып алып, сол жақта тұрғн бос мүшелерді таңбасын қарама-қарсы таңбаға өзгертіп оң жаққа көшіру керек.
3. Теңдеудің екі жағындағы ұқсас мүшелерді біріктіргенде
ах=b
түріндегі сызықтық теңдеу шығады. Теңдеудің екі жағында да
х
-тің коэффициентін
а
-ға бөлу арқылы
х
=
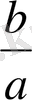 түбірін табамыз. Егер. 1.
а
=0,
b
≠0 болса 0∙
х
=
b
теңдеуінің түбірі болмайды. 2.
а
=0,
b
≠0 болса, кез келген сан ноль х=b теңдеудің түбірі болады. Егер теңдеудің құрамында жақшасы бар өрнек болса, алдында «+» таңбасы немесе «-» таңбасы бар жақшаларды ашу ережесіне және көбейтудің үлестірімділік заңын қолданып жақшаларын ашу керек. содан кейін, жоғарыдағы алгеритім бойынша, орындау керек.
түбірін табамыз. Егер. 1.
а
=0,
b
≠0 болса 0∙
х
=
b
теңдеуінің түбірі болмайды. 2.
а
=0,
b
≠0 болса, кез келген сан ноль х=b теңдеудің түбірі болады. Егер теңдеудің құрамында жақшасы бар өрнек болса, алдында «+» таңбасы немесе «-» таңбасы бар жақшаларды ашу ережесіне және көбейтудің үлестірімділік заңын қолданып жақшаларын ашу керек. содан кейін, жоғарыдағы алгеритім бойынша, орындау керек.
3-мысал: 3 х +7=9 х +19
3 х -9 х =19-7
-6
х
=12
 х
=
х
=
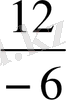
 х
=-2:
х
=-2:
4-мысалы: 3( х -2) -2(4 х -1) =4(1- х )
3 х -6-8 х +2=4-4 х
3
х
-8
х
+4
х
=4+6-2
 -
х
=8
-
х
=8
 х
=-8:
х
=-8:
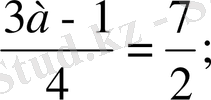
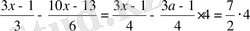
Теңдеулерін шешкенде теңдеудің екі жағындағы бөлшектердің әрқайсын бөлімдерінің ең кіші ортақ еселігіне көбейтіп теңдеуді бөлімінен құтқарамыз.
Егер жақшасы бар теңдеу шықса, жақшаларды ашып, жоғарыдағы алгоритм бойынша орындау керек.
1. 2 Квадрат теңдеулер
Квадрат теңдеулерді шешу және формуласы.
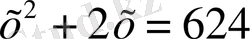 . Бұл теңдеудің екі жағы да белгісізге қатысты бүтін өрнек. Мұндай теңдеулер бүтін өрнекті теңдеулер деп аталады. Бұл теңдеуде бір белгісізі бар және оның ең жоғарғы дәрежесі екіге тең болғандықтан бір айнымалыға тәуелді
екінші дәрежелі бүтін өрнекті теңдеу
деп аталады. Бұл теңдеуді
. Бұл теңдеудің екі жағы да белгісізге қатысты бүтін өрнек. Мұндай теңдеулер бүтін өрнекті теңдеулер деп аталады. Бұл теңдеуде бір белгісізі бар және оның ең жоғарғы дәрежесі екіге тең болғандықтан бір айнымалыға тәуелді
екінші дәрежелі бүтін өрнекті теңдеу
деп аталады. Бұл теңдеуді
 түрінде жазсақ. Онда квадрат теңдеудің жалпы түрі
түрінде жазсақ. Онда квадрат теңдеудің жалпы түрі
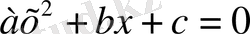 болып жазылады. Мұндағы
болып жазылады. Мұндағы
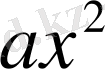 екінші дәрежелі мүше,
а
оның коэффициенті,
екінші дәрежелі мүше,
а
оның коэффициенті,
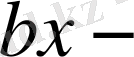 бірінші дәрежелі мүше,
бірінші дәрежелі мүше,
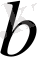 оның коэффициенті, ал
с
-босмүше деп аталады. М:
оның коэффициенті, ал
с
-босмүше деп аталады. М:
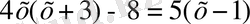 теңдеуін квадрат теңдеу түрінде жазайық. Жақшаларды ашсақ
теңдеуін квадрат теңдеу түрінде жазайық. Жақшаларды ашсақ
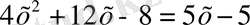 шығады. Ұқсас мүшелерін біріктіріп жазсақ,
шығады. Ұқсас мүшелерін біріктіріп жазсақ,
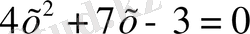 түрге келеді. Бұл теңдеудің екінші дәрежелі мүшесінің коэффициенті 4, бірінші дәрежелі мүшесінің коэффициенті 7, бос мүше -3 екенін көреміз.
түрге келеді. Бұл теңдеудің екінші дәрежелі мүшесінің коэффициенті 4, бірінші дәрежелі мүшесінің коэффициенті 7, бос мүше -3 екенін көреміз.
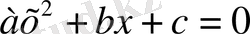 теңдеуіндегі
b
мен
c
-ның ең болмағанда бірі нольге тең болатын теңдеуді
толымсыз екінші дәрежелі теңдеу
дейміз.
теңдеуіндегі
b
мен
c
-ның ең болмағанда бірі нольге тең болатын теңдеуді
толымсыз екінші дәрежелі теңдеу
дейміз.
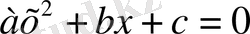 (
а
≠0) теңдеуін квадратқа толықтыру тәсілі бойынша түрлендірейік. Теңдеудің екі жағын
а
-ға бөлсек және бос мүшені теңдеудің оң жағына шығарсақ,
(
а
≠0) теңдеуін квадратқа толықтыру тәсілі бойынша түрлендірейік. Теңдеудің екі жағын
а
-ға бөлсек және бос мүшені теңдеудің оң жағына шығарсақ,
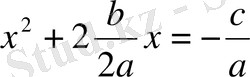 . Осы теңдеудің екі жағына бірінші дәрежелі мүшенің коэффициентінің жартысының квадратын қосақ,
. Осы теңдеудің екі жағына бірінші дәрежелі мүшенің коэффициентінің жартысының квадратын қосақ,
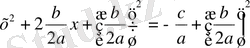 .
.
Бұдан
(1)
шығады.
1)
а
≠0 болғандықтан
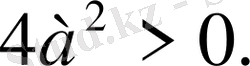
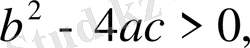 болғанда (яғни
болғанда (яғни
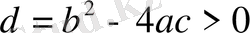 ) .
) .
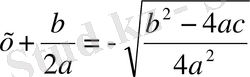 немесе
немесе
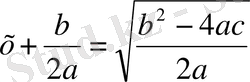 Бұдан
Бұдан
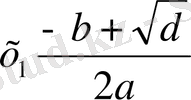 ;
;
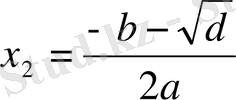 . (2)
. (2)
Мұндағы
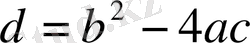 квадрат теңдеудің дискориминанты деп аталады. (2) формула
квадрат теңдеудің дискориминанты деп аталады. (2) формула
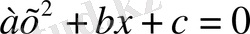 теңдеуінің түбірлерін табатын формула болып табылады. (1) теңдеудегі
d
=0 болса, онда
теңдеуінің түбірлерін табатын формула болып табылады. (1) теңдеудегі
d
=0 болса, онда
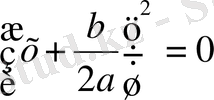 . Бұдан
. Бұдан
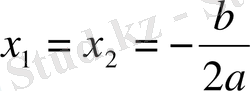 теңдеуінің өзара тең екі түбірі бар. 2)
d
<0 болса, онда
теңдеуінің өзара тең екі түбірі бар. 2)
d
<0 болса, онда
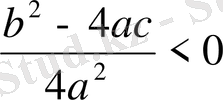 сондықтан (1) теңдеудің түбірі блмайды.
сондықтан (1) теңдеудің түбірі блмайды.
Сонымен,
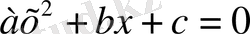 теңдеуінің түбірлері
a, b, c
коэффициентіне тәуелді екенін байқауға болады. Бір белгісізі бар екінші дәрежелі теңдеуді шешу үшін алдымен теңдеуді
теңдеуінің түбірлері
a, b, c
коэффициентіне тәуелді екенін байқауға болады. Бір белгісізі бар екінші дәрежелі теңдеуді шешу үшін алдымен теңдеуді
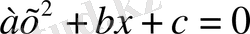 түрге келтіреді. Теңдеудегі
a, b, c-
ның мәндерін формулаға қойып түбірлерін табады.
түрге келтіреді. Теңдеудегі
a, b, c-
ның мәндерін формулаға қойып түбірлерін табады.
Екінші дәрежелі квадрат теңдеудің түбірлерін басқа тәсілмен табуға болады. Ол үшін
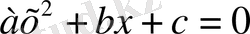 теңдеуінің екі бөлігін де 4
а
-ға көбейтеміз, сонда
теңдеуінің екі бөлігін де 4
а
-ға көбейтеміз, сонда
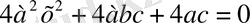 немесе
немесе
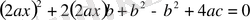 ,
,
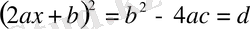 тікелей түбір тапсақ,
тікелей түбір тапсақ,
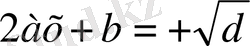 ,
,
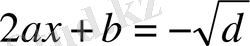 бұл арадан
х
-ті тапсақ,
бұл арадан
х
-ті тапсақ,
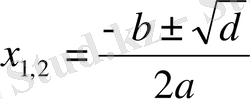 (2) формула шығады.
(2) формула шығады.
1-мысал
.
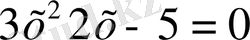 теңдеуін шешейік.
а
=3
, b=
2
, c=-5
болғандықтан,
теңдеуін шешейік.
а
=3
, b=
2
, c=-5
болғандықтан,
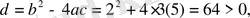
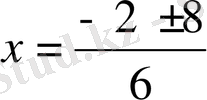 , бұдан
, бұдан
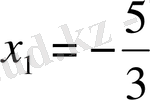 ,
,
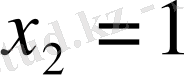 .
.
2-мысал
.
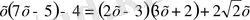 теңдеуін шешейік. Берілген теңдеуді
теңдеуін шешейік. Берілген теңдеуді
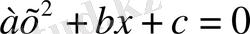 түрінде жазамыз:
түрінде жазамыз:
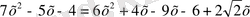 ,
,
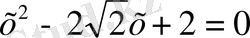 . Соңғы теңдеудегі
а=1, b=-2
. Соңғы теңдеудегі
а=1, b=-2
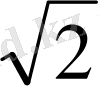 ,
c=2, d=b
2
-4ac=
,
c=2, d=b
2
-4ac=
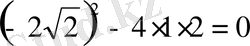 ,
d=0.
Бұдан
,
d=0.
Бұдан
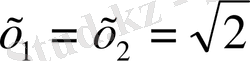 .
.
Егер квадрат теңдеудің бірінші дәрежелі қосылғышының коэффициенттері жұп сан, яғни
b=
2
k
болса, онда теңдеудің дискриминанты
d=4k
2
-4ac=4(k
2
-ac),
мұны (2) формулаға қойсақ,
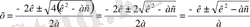
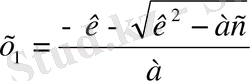 ,
,
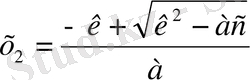 (3)
(3)
Сонымен, квадрат теңдеудің бірінші дәрежелі қосылғышының
коэффициенттері жұп сан болғанда теңдеудің түбірлерін (3) формуламен табу тиімді болады.
3-мысал
.
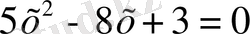 теңдеуін шешейік.
b=8
жұп сан болғандықтан (3) үшінші формуланы пайдаланамыз:
d
=
теңдеуін шешейік.
b=8
жұп сан болғандықтан (3) үшінші формуланы пайдаланамыз:
d
=
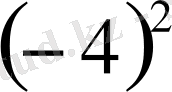 -5·3=1,
-5·3=1,
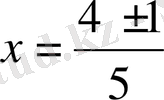 , бұдан
, бұдан
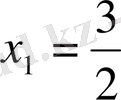 ;
;
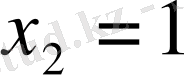 .
.
Толымсыз квадрат теңдеулерді шешу жолдарын қарастырайық.
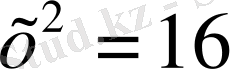 теңдеуін шешсек,
х
шамасы 16-ның квадра түбірі болғандықтан,
теңдеуін шешсек,
х
шамасы 16-ның квадра түбірі болғандықтан,
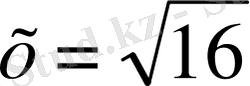 , яғни
, яғни
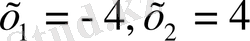 . Мұндағы
. Мұндағы
 және
және
 бір белгісізі бар екінші дәрежелі толымсыз квадрат теңдеудің түбірлері. Көрсетілген толымсыз квадрат теңдеуді шешудің мұндай жолы
тікелей түбір табу тәсілі
деп аталады.
бір белгісізі бар екінші дәрежелі толымсыз квадрат теңдеудің түбірлері. Көрсетілген толымсыз квадрат теңдеуді шешудің мұндай жолы
тікелей түбір табу тәсілі
деп аталады.
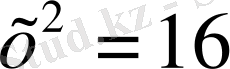 теңдеуді
теңдеуді
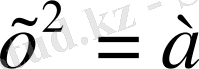 теңдеуінің дербес жағыдайы болады.
теңдеуінің дербес жағыдайы болады.
Теорема.
Егер
 болса, онда
болса, онда
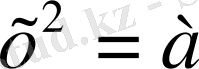 теңдеуінің
теңдеуінің
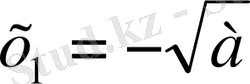 ,
,
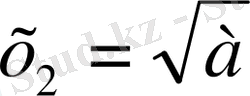 қарама-қарсы таңбалы екі шешуі болады.
а
санын теңдеудің сол жағына шығарсақ,
қарама-қарсы таңбалы екі шешуі болады.
а
санын теңдеудің сол жағына шығарсақ,
 ,
,
 болғандықтан арифметикалық квадрат теңдеудің анықтамасы бойынша
болғандықтан арифметикалық квадрат теңдеудің анықтамасы бойынша
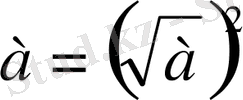 . Сондықтан
. Сондықтан
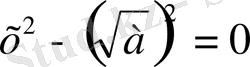 теңдеуін жазуға болады. Мұны көбейткіштерге жіктесек,
теңдеуін жазуға болады. Мұны көбейткіштерге жіктесек,
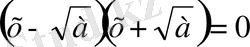 . Яғни
. Яғни
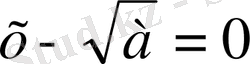 немесе
немесе
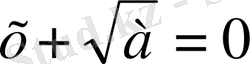 .
.
Бұдан
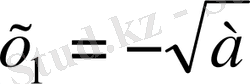 ,
,
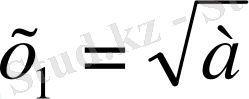 .
.
1-мысал
.
 теңдеуін шешейік.
теңдеуін шешейік.
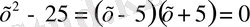 екенін ескерсек, бұдан
екенін ескерсек, бұдан
 немесе
немесе
 , бұдан
, бұдан
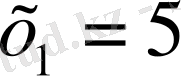 ,
,
 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz