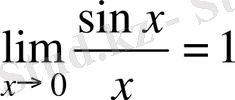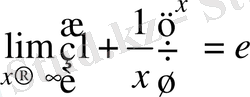Дифференциалдық есептер: функция ұғымы, шектер, үзіліссіздік және туындының экономикалық мағынасы


ІІ- МОДУЛЬ. ДИФФЕРЕНЦИАЛДЫҚ ЕСЕПТЕУЛЕР
БЕСІНШІ ЛЕКЦИЯ
ФУНКЦИЯ ҰҒЫМЫ
Функция немесе функциялық тәуелділік ұғымы түрлі шамалар, экономикалық көрсеткіштер арасындағы байланыстарды моделдейтін математиканың маңызды ұғымы.
Анықтама.
Х жиынының әрбір х элементіне (
 ) белгілі бір заң немесе ереже бойынша У жиынының у элементі сәйкес қойылса, онда Х жиынында
функция
берілген деп атайды.
) белгілі бір заң немесе ереже бойынша У жиынының у элементі сәйкес қойылса, онда Х жиынында
функция
берілген деп атайды.
х және у шамаларының арасындағы функциялық тәуелділікті y=f(x) деп белгілейді, мұндағы х - аргумент(тәуелсіз айнымалы), у - функция(тәуелді айнымалы), f - ереже немесе заң.
Берілген функция анықталатын х аргументтерінің жиынын функцияның анықталу облысы деп, ал сәйкес у айнымалылардың жиынын функцияның мәндер жиыны деп атайды. Әдетте анықталу облысын D(f) деп, ал мәндер жиынын E(f) деп белгілейді.
Функция түрлі тәсілдермен берілуі мүмкін. Ең көп және маңызды берілу түрлері: аналитикалық(формула түрінде), кестелік және графиктік.
Мысал ретінде заттың бағасы ( р ) мен сол затқа деген сұраныс ( q ) арасындағы байланысты қарастырайық:
Кестеден көрініп тұрғандай, заттың бағасы артқан сайын, оған деген сұраныс төмендейді екен. Бұл байланысты графиктік түрде де беруге болады (1-сурет) .
Р
300
250
200
150
100
0 6 9 12 15 18 q
Заттың бағасы мен сұраныс арасында түзу сызықты p=kq+b байланыс байқалады. Берілген мәндерді пайдаланып бұл байланысты табу қиын емес:
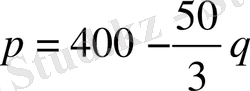 .
.
Кестенің төменгі жолындағы сұраныстың мәндерін q орнына қойсақ жоғары жолдағы бағаның сәйкес мәндері шығып отырады. Сонымен, функцияның аналитикалық берілуінен оның кестелік және графиктік түрлерін оңай алуға болады екен.
Функция қасиеттері. y=f(x) функциясын қарастырайық.
1. Шенелген функция . Егер функцияның анықталу облысындағы кез келген х үшін қандай да бір М нақты сан табылып f(x) <M теңсіздігі орындалса функция жоғарыдан шенелген , ал f(x) >M теңсіздігі орындалса функция төменнен шенелген деп аталады (2 а, б-сурет) .
Егер функцияның анықталу облысындағы кез келген х үшін қандай да бір М нақты сан табылып f(x) <M теңсіздігі орындалса функция шенелген деп аталады (2 в-сурет) .
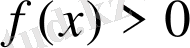
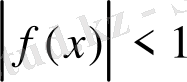
2 а-сурет 2 б-сурет 2 в-сурет
2. Жұп және тақ функция . Егер функцияның анықталу облысындағы кез келген х үшін
f(-x) =f(x)
теңдігі орындалса функция жұп деп, ал
f(-x) =-f(x)
теңдігі орындалса функция
тақ
деп аталады. Мысалы,
y=x
2n
, y=x
функциялары жұп, ал y
=x
2n+1
,
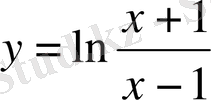 функциялары тақ болады.
функциялары тақ болады.
Жұп функция графигі Оу осіне, ал тақ функция графигі О(0, 0) - координаталар басына қарағанда симметриялы болады.
Жұп функциялардың қосындысы, айырымы, көбейтіндісі, бөліндісі - жұп функция болады.
Тақ функциялардың қосындысы мен айырымы - тақ, ал көбейтіндісі мен бөліндісі - жұп функция болады.
Егер функция үшін f(-x) =f(x) және f(-x) =-f(x) теңдіктерінің екеуі де орындалмаса функция жұп та, тақ та емес (бейтарап) болады. Мысалы, y=x 2 +х функциясы жұп та, тақ та емес.
3. Периодты функциялар . Егер функцияның анықталу облысындағы кез келген х үшін
f(x+Т) =f(x)
теңдігі орындалатындай
Т
сан табылса функция
периодты
деп аталады. Осындай
Т
сандардың ең кішісі функцияның
негізгі периоды
деп аталады. Мысалы,
y=sin(x), y=cos(x)
(бұлардың негізгі периоды 2
 ),
y=tg(x), y=ctg(x)
(бұлардың негізгі периоды
),
y=tg(x), y=ctg(x)
(бұлардың негізгі периоды
 ) - периодты функциялар.
) - периодты функциялар.
4. Бірсазды (монотонды) функциялар. Егер функцияның анықталу облысындағы кез келген х 1 , х 2 ( х 1 < х 2 ) мәндер үшін
f(х 1 ) < f(х 2 ) теңсіздігі орындалса, функция өспелі (3 а-сурет),
f(х 1 ) > f(х 2 ) теңсіздігі орындалса, функция кемімелі (3 б-сурет) ,
f(х
1
)
 f(х
2
)
теңсіздігі орындалса, функция
кемімейтін
(3 в-сурет),
f(х
2
)
теңсіздігі орындалса, функция
кемімейтін
(3 в-сурет),
f(х
1
)
 f(х
2
)
теңсіздігі орындалса, функция
өспейтін
(3 г-сурет)
f(х
2
)
теңсіздігі орындалса, функция
өспейтін
(3 г-сурет)
деп аталады.
3 а-сурет 3 б-сурет 3 в-сурет 3 г-сурет
Егер қандай да бір аралықта функция не тек өспелі немесе тек кемімелі болса, оны осы аралықта монотонды (бірсазды) деп айтады.
5. Кері функция . y=f(x) функциясының кері функциясын табу үшін алдымен х аргументті у айнымалы арқылы өрнектейміз, х=g(у) , одан кейін, тәуелсіз аргумент х деп ал ал тәуелді айнымалы у деп белгілеу қалыптасқандықтан, алынған өрнектегі х пен у орындарын алмастырамыз, у=g(х) . Пайда болған g(х) функция берілген f(x) функцияға кері функция болады.
Өзара кері функциялардың графигі y=x (бірінші және үшінші декарттық бұрыштардың биссектрисасы) түзуіне қарағанда симметриялы болады.
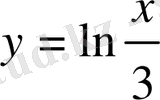 Мысалы
,
Мысалы
,
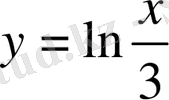 функциясының кері функциясын табау керек (4-сурет) .
функциясының кері функциясын табау керек (4-сурет) .
Шешуі . Алдымен теңдеудегі х аргументті у айнымалы арқылы өрнектеу үшін х -ке қатысты шешеміз:
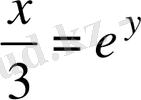 осыдан
осыдан
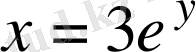 .
.
Енді алынған өрнектегі
х
пен
у
орындарын алмастырамыз:
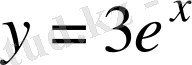 . Сонда берілген
. Сонда берілген
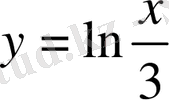 функцияға кері функция
функцияға кері функция
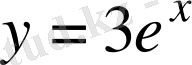 болады.
болады.
Берілген функцияның анықталу облысы оған кері функцияның мәндер жиыны болады да, мәндер жиыны кері функцияның анықталу облысы болады.
Аралықта монотонды өсетін немесе монотонды кемитін функциялардың ғана кері функциялары табылады.
6. Күрделі функция . y=f(g(x) ) түрінде берілген функцияны күрделі функция дейді. Кейде күрделі функцияны мынадай түрде де береді: y=f(u) мұндағы u=g(x) . Бұл жағдайда u - аралық айнымалы, ал х - тәуелсіз аргумент болады.
Мысалы
,
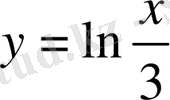 функциясы күрделі функция. Оны
функциясы күрделі функция. Оны
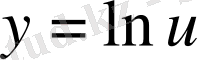 , мұндағы
, мұндағы
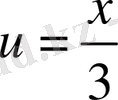 түрінде жазуға болады.
түрінде жазуға болады.
7. Айқын емес түрде берілген функция. Егер функция
F(x, y) =0 ,
яғни
y
айнымалыға қатысты шешілмеген түрінде, берілсе функция айқын емес түрде берілген дейміз. Жоғарыда қарастырылған
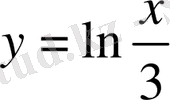 функцияны айқын емес түрде былай жазамыз:
функцияны айқын емес түрде былай жазамыз:
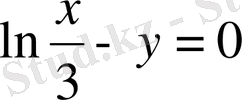 .
.
КҮРДЕЛІ ФУНКЦИЯ ГРАФИГІН БЕЛГІЛІ ФУНКЦИЯ ГРАФИГІН ТҮРЛЕНДІРУ АРҚЫЛЫ САЛУ
y=f(х) функция графигі белгілі болса төмендегі функциялардың графиктерін салуға болады:
- y=f(х) +b. Бұл функция графигі берілген функция графигін Оу осі бойыменbшамаға (b>0болса жоғары, b<0болса төмен) жылжыту арқылы салынады (5а-сурет) .
- y=f(х+a) . Бұл функция графигі берілген функция графигін Ох осі бойыменaшамаға (a>0болса солға, a<0болса оңға) жылжыту арқылы салынады (5б-сурет) .
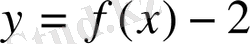
- y= - f(х) . Бұл функция графигі берілген функция графигіне Ох осіне қарағанда симметриялы орналасады (6а-сурет) .
- y=f(-х) . Бұл функция графигі берілген функция графигіне Оу осіне қарағанда симметриялы орналасады (6б-сурет) .

6а-сурет 6б-сурет
- y=kf(х) . Егерk>1болса функция мәніkесе артады, яғни график Оу осі бойымен созылады. Егерk<1болса функция мәніkесе кемиді, яғни график Оу осі бойымен сығылады (7а-сурет) .
- y=f(kх) . Егерk>1болса берілген функция графигін Ох осі бойыменkесе сығылады. Егерk<1болса берілген функция графигін Ох осі бойыменесе созылады (7б-сурет) .
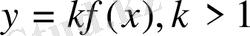
7а-сурет 7б-сурет
- y=f(х) . Егерболса, болады, яғни Ох осінің жоғары жағында жатқан функция графигін өзгертусіз қалдыру керек. Егерболса, болады, яғни Ох осінің төменгі жағында жатқан функция графигін Ох осіне қарағанда симметриялы жоғары бөлікке бейнелеу керек (8а-сурет) .
- y=f(х) . Функция жұп, сондықтан функция графигі Оу осіне қарағанда симметриялы болады. болса, болады, яғни Оу осінің оң жағында жатқан функция графигін өзгертусіз қалдыру керек және осы бөлікті Оу осіне қарағанда симметриялы сол бөлікке бейнелеу керек (8б-сурет) .
8а-сурет 8б-сурет
ШЕК ҰҒЫМЫ
Экономикада көптеген шамалардың орташа мәндерін қарастырады. Мысалы, орташа шығын, орташа табыс, орташа пайда, т. с. с. Сонымен қатар, қандай да бір шаманы көбейткенде немесе азайтқанда нәтиже қаншалықты өзгеретіндігін білу үшін математиканың шектік талдау әдісін қолдану керек болады. Шектік талдау негізінде сіздерге мектептен таныс шек ұғымы жатыр.
Демография саласындағы адам жасының орташа ұзақтығын есептеу де шекке мысал бола алады. Айталық х жастағы адамның енді алдында жасайтын өмірінің орташа ұзақтығы е х дейік. Әрине, жас балаға қарағанда 80 жастағы қарт адам үшін бұл орташа ұзақтық бірталай аз екенін түсіну қиын емес. Жас ұлғайған сайын алдымыздағы жастың ұзақтығы е х әрине қысқарады. Бірақ, алдын ала е х нолге тең болатын х -ті көрсету мүмкін емес. Олай болғанда адам сол жасқа келгенде бірден өлу керек болар еді. Сонымен е х шамасы, х өскен сайын, біртіндеп нолге ұмтылады.
Енді функция шегінің анықтамасына көшейік. y=f(х) функциясы қандай да бір х 0 нүкте маңайында анықталған болсын.
Анықтама.
Егер алдын ала берілген, мейілінше аз
 санына
санына
 саны табылып,
саны табылып,
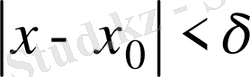 шартын қанағаттандыратын барлық х үшін
шартын қанағаттандыратын барлық х үшін
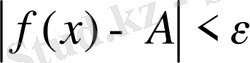 теңсіздігі орындалса, онда А саны
f(x) функциясының х аргумент х
0
-ге ұмтылғандағы шегі
деп аталады да, былай жазылады:
теңсіздігі орындалса, онда А саны
f(x) функциясының х аргумент х
0
-ге ұмтылғандағы шегі
деп аталады да, былай жазылады:
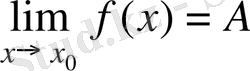 .
.
Анықтамадағы
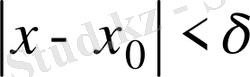 теңсіздікті ашсақ, мынадай қос теңсіздік аламыз:
теңсіздікті ашсақ, мынадай қос теңсіздік аламыз:
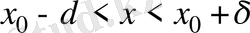 .
.
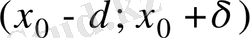 интервалды
интервалды
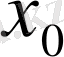 нүктесінің
нүктесінің
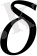 -маңайы
дейді.
-маңайы
дейді.
Сол сияқты
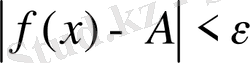 теңсіздікті ашсақ:
теңсіздікті ашсақ:
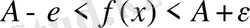 .
.
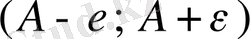 интервалды
А
нүктесінің
интервалды
А
нүктесінің
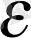 -маңайы
дейді.
-маңайы
дейді.
y
А+

y=f(x)
A
A+

0 x
0
-
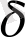 x
0
х
0
+
x
0
х
0
+
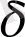 x
x
Енді анықтаманы сурет бойынша айтсақ: Алдын ала берілген,
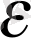 санына
санына
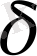 саны табылып, аргумент мәндері
саны табылып, аргумент мәндері
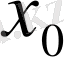 нүктесінің
нүктесінің
 -маңайына тиісті болғанда функцияның сәйкес мәндері
А
нүктесінің
-маңайына тиісті болғанда функцияның сәйкес мәндері
А
нүктесінің
 -маңайында жатса, А саны
f(x)
функциясының
х
аргумент
х
0
-ге ұмтылғандағы шегі деп аталады.
-маңайында жатса, А саны
f(x)
функциясының
х
аргумент
х
0
-ге ұмтылғандағы шегі деп аталады.
Мысал . Өндіріс орны шығаратын заттың бір данасының бағасы y пен оған деген сұраныс x (мың дана) арасындағы байланыс мынадай қатынаспен анықталған:
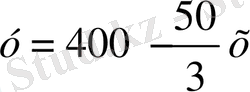 .
.
Заттың бір данасының бағасы 190 - 210 теңге арасында тұруы үшін өндіріс орнының өнім көлемі қалай өзгеруі керек (9-сурет) ?
у
210
200
190
0 11, 4 12 12, 6 х
Шешуі.
(190; 210) интервалының ортасы
А=200
теңге, олай болса
 =
10
. Шек анықтамасындағы
=
10
. Шек анықтамасындағы
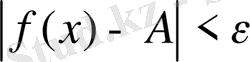 теңсіздігін қолданайық:
теңсіздігін қолданайық:
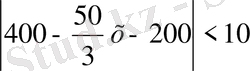 . Осы теңсіздікті түрлендіріп ықшамдасақ мынадай теңсіздік аламыз:
. Осы теңсіздікті түрлендіріп ықшамдасақ мынадай теңсіздік аламыз:
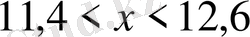 .
.
Соңғы теңсіздікті мынадай
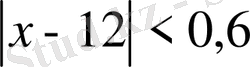 түрге келтіріп жазсақ, есеп сұрағына жауап беруге болады: Заттың бір данасының бағасының 200 теңгеден ауытқуы 10 теңгеден артпауы үшін, өндіріс орны өнім көлемінің өзгеруін 0, 6 мың данадан асырмауы керек екен.
түрге келтіріп жазсақ, есеп сұрағына жауап беруге болады: Заттың бір данасының бағасының 200 теңгеден ауытқуы 10 теңгеден артпауы үшін, өндіріс орны өнім көлемінің өзгеруін 0, 6 мың данадан асырмауы керек екен.
Функция шегінің қасиеттері.
Айталық
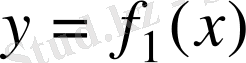 және
және
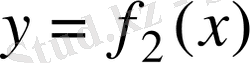 функцияларының
функцияларының
 жағдайда
жағдайда
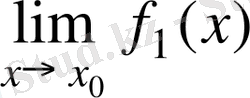 және
және
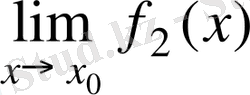 шектері бар болсын.
шектері бар болсын.
- Екі функцияның алгебралық қосындысының шегі шектердің алгебралық қосындысына тең болады, яғни
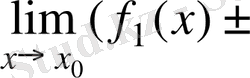
=
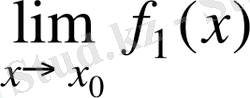
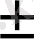
.
- Екі функцияның көбейтіндісінің шегі шектердің көбейтіндісіне тең болады, яғни
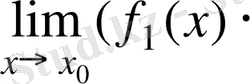
=
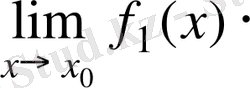
.
Салдар.
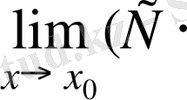
= С
, мұндағы С - const.
- Екі функцияның қатынасының шегі шектердің қатынасына тең болады (әрине, егер бөлімдегі функция нолден өзгеше болса), яғни
=
.
Мысал
.
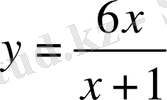 функциясының
функциясының
 жағдайдағы шегін табу керек.
жағдайдағы шегін табу керек.
Шешуі
. Қысқаша айтсақ
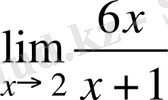 шек есептеу керек. Функция шегінің қасиеттерін қолданып есептейік:
шек есептеу керек. Функция шегінің қасиеттерін қолданып есептейік:
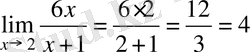 .
.
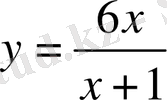 функциясының
функциясының
 жағдайдағы шегі 4 болады екен.
жағдайдағы шегі 4 болады екен.
БІРІНШІ ЖӘНЕ ЕКІНШІ ТАМАША ШЕКТЕР
Теорема.
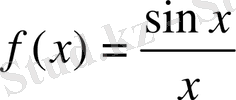 функциясы x=0 нүктеде анықталмаған, бірақ
функциясы x=0 нүктеде анықталмаған, бірақ
 жағдайда шегі бар және
жағдайда шегі бар және
Осы шекті бірінші тамаша шек деп атайды.
Бірінші тамаша шек салдары:
1)
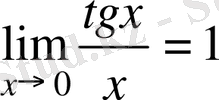 , 2)
, 2)
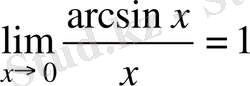 , 3)
, 3)
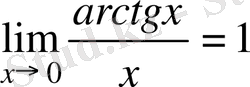 .
.
Мысал.
а)
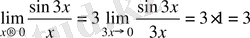 .
.
б)
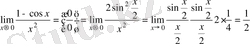 .
.
Теорема.
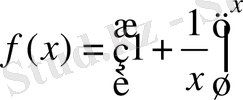 функциясының
функциясының
 жағдайда шегі бар және
жағдайда шегі бар және
Осы шекті
екінші тамаша шек
деп атайды. Мұндағы
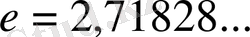 иррационал саны Эйлер саны екені белгілі.
иррационал саны Эйлер саны екені белгілі.
Екінші тамаша шек салдары:
1)
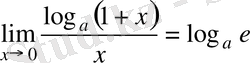 ,
a=e болғанда
,
a=e болғанда
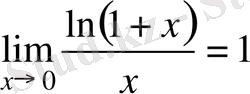 ;
;
2)
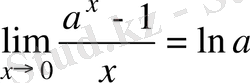 ,
a=e болғанда
,
a=e болғанда
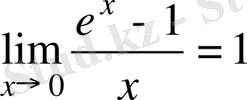 ;
;
3)
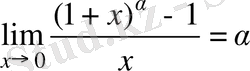
Мысал. а)
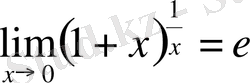 екенін көрсет.
екенін көрсет.
Шешуі
.
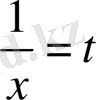 деген білгілеу енгізейік. Осыдан
деген білгілеу енгізейік. Осыдан
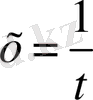 . Және де
. Және де
 кезде
кезде
 . Енді шек есептесек
. Енді шек есептесек
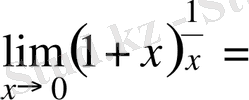
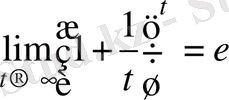 .
.
б)
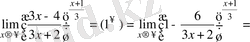
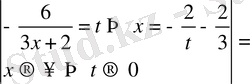
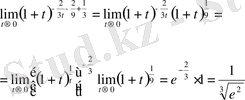
АҚЫРСЫЗ АЗ ЖӘНЕ АҚЫРСЫЗ ҮЛКЕН ФУНКЦИЯЛАР
Анықтама.
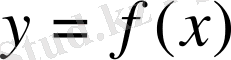 функциясының
функциясының
 жағдайда шегі ноль болса, яғни
жағдайда шегі ноль болса, яғни
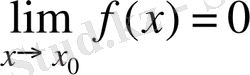 , онда
, онда
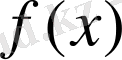 функциясы
функциясы
 жағдайда
ақырсыз аз функция
деп аталады.
жағдайда
ақырсыз аз функция
деп аталады.
Осы анықтаманы “
 ” тілінде былай да айтуға болады: Кез келген
” тілінде былай да айтуға болады: Кез келген
 үшін
үшін
 саны табылып,
саны табылып,
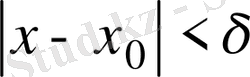 теңсіздігін қанағаттандыратын барлық х-тер үшін
теңсіздігін қанағаттандыратын барлық х-тер үшін
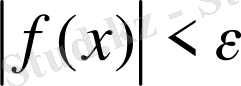 теңсіздігі орындалса,
теңсіздігі орындалса,
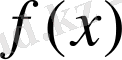 функциясы
функциясы
 жағдайда
ақырсыз аз функция
деп аталады.
жағдайда
ақырсыз аз функция
деп аталады.
Ақырсыз аз функция қасиеттері.
- бар болса, ондафункциясын осы А саны менжағдайда ақырсыз аз болатынфункция қосындысы түрінде жазуға болады, яғни.
- Ақырсыз аз функцияның шенелген функцияға (сонмен қатар, тұрақтыға, басқа ақырсыз азға) көбейтіндісі ақырсыз аз функция болады.
- Ақырсыз аз функцияның шегі нолден өзге функцияға қатынасы ақырсыз аз функция болады.
Анықтама.
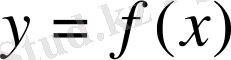 функциясының
функциясының
 жағдайда шегі шексіздік болса, яғни
жағдайда шегі шексіздік болса, яғни
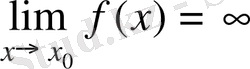 , онда
, онда
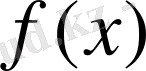 функциясы
функциясы
 жағдайда
ақырсыз үлкен функция
деп аталады.
жағдайда
ақырсыз үлкен функция
деп аталады.
Ақырсыз аз функция мен ақырсыз үлкен функция арасында мынадай байланыс бар:
Егер
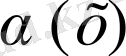 функциясы
функциясы
 жағдайда ақырсыз аз болса,
жағдайда ақырсыз аз болса,
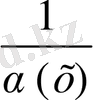 функциясы
функциясы
 жағдайда ақырсыз үлкен болады.
жағдайда ақырсыз үлкен болады.
Мысалы
,
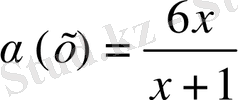 функциясы
функциясы
 жағдайда ақырсыз аз функция болады.
жағдайда ақырсыз аз функция болады.
Шынында да,
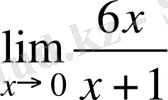 шегін есептейік.
шегін есептейік.
.
Ал
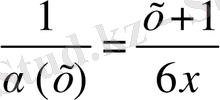 функциясы
функциясы
 жағдайда ақырсыз үлкен функция болады, яғни оның шегі шексіздік.
жағдайда ақырсыз үлкен функция болады, яғни оның шегі шексіздік.
Шынында да, шегін есептейік.
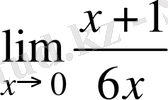
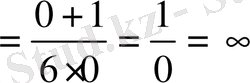 .
.
Мұндағы
 қатынасты шектер тілінде “ақырсыз азға кері шама ақырсыз үлкен” дейді де, шексіздікке теңестіреді.
қатынасты шектер тілінде “ақырсыз азға кері шама ақырсыз үлкен” дейді де, шексіздікке теңестіреді.
Ақырсыз аз функциялар нолге әртүрлі жылдамдықпен жақындайды. Көптеген жағдайда ақырсыз аздардың нолге ұмтылу жылдамдығын анықтау үшін оларды өзара салыстыру керек болады. Салыстыру үшін олардың қатынасының
 жағдайдағы шегін қарастырады.
жағдайдағы шегін қарастырады.
Айталық
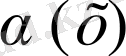 және
және
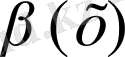
 жағдайда ақырсыз аз функциялар және
жағдайда ақырсыз аз функциялар және
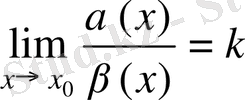 болсын. Онда, егер
болсын. Онда, егер
1)
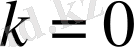 болса
болса
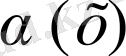
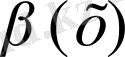 -ға қарағанда жоғары ретті ақырсыз аз деп;
-ға қарағанда жоғары ретті ақырсыз аз деп;
2)
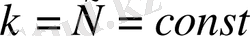
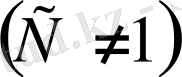 болса
болса
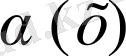 мен
мен
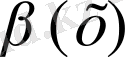 бірдей ретті ақырсыз аз деп;
бірдей ретті ақырсыз аз деп;
3)
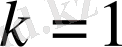 болса
болса
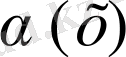 мен
мен
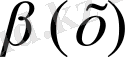 эквивалентті ақырсыз аз деп
эквивалентті ақырсыз аз деп
аталады.
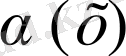 мен
мен
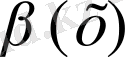 эквивалентті дегенді
эквивалентті дегенді
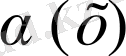 ~
~
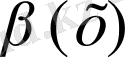 деп жазады.
деп жазады.
Егер
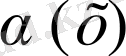 функциясы
функциясы
 жағдайда ақырсыз аз болса, онда
жағдайда ақырсыз аз болса, онда
1.
,
,
,
;
2.
,
;
3.
,
;
4.
,
;
5.
.
1. -5. қатынастар эквивалентті функциялар кестесін береді. Бұл кестені шек есептеу кезінде мына теоремаға сүйеніп қолдануға болады.
Теорема.
Егер
 жағдайда
жағдайда
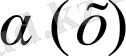 ~
~
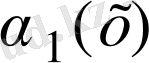 және
және
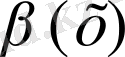 ~
~
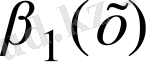 болса, онда
болса, онда
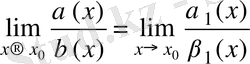 .
.
Мысал.
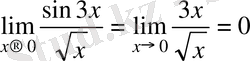 . Мұнда
. Мұнда
 жағдайда
жағдайда
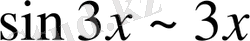 болғандықтан
болғандықтан
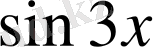 орнына
орнына
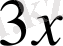 алынды.
алынды.
ФУНКЦИЯ ҮЗІЛІССІЗДІГІ. ҮЗІЛІС ТҮРЛЕРІ
Анықтама.
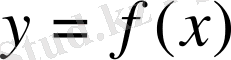 функциясының
функциясының
 жағдайда шегі функцияның сол нүктедегі мәніне тең болса, яғни
жағдайда шегі функцияның сол нүктедегі мәніне тең болса, яғни
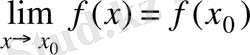 ,
функция
,
функция
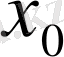 нүктесінде
үзіліссіз
деп аталады.
нүктесінде
үзіліссіз
деп аталады.
Егер
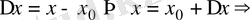
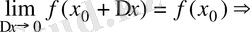
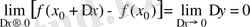 .
.
Сонда функция үзіліссіздігінің анықтамасын былай да айтуға болады: Берілген нүктеде аргументтің ақырсыз аз өсімшесіне функцияның да ақырсыз аз өсімшесі сәйкес келсе, яғни

функция
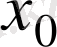 нүктесінде үзіліссіз деп аталады.
нүктесінде үзіліссіз деп аталады.
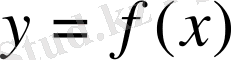 функциясы қандай да бір аралықтың үзіліссіз болуы үшін, ол сол аралықтың әрбір нүктесінде үзіліссіз болуы керек.
функциясы қандай да бір аралықтың үзіліссіз болуы үшін, ол сол аралықтың әрбір нүктесінде үзіліссіз болуы керек.
Үзіліссіз функция қасиеттері.
- функциясынүктесінде үзіліссіз, алфункциясынүктесінде үзіліссіз болса, күрделі функциясынүктесінде үзіліссіз болады және
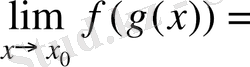
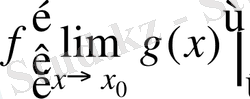 .
.
- Нүктеде үзіліссіз функциялардың алгебралық қосындысы, көбейтіндісі және қатынасы (бөліміндегі функция нолден өзге болғанда) үзіліссіз функция болады.
Анықтама.
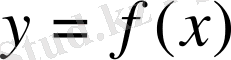 функциясының
функциясының
 жағдайда шегі функцияның сол нүктедегі мәніне тең болмаса, яғни
жағдайда шегі функцияның сол нүктедегі мәніне тең болмаса, яғни
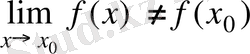 ,
функция
,
функция
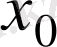 нүктесінде үзілісті функция
деп, ал
нүктесінде үзілісті функция
деп, ал
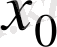 нүктені функцияның үзіліс нүктесі
деп атайды.
нүктені функцияның үзіліс нүктесі
деп атайды.
Біржақты шектер ұғымын енгізейік.
Айталық
 және
және
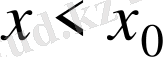 , онда
, онда
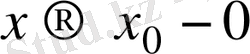 деп жазады, ал осы жағдайдағы
деп жазады, ал осы жағдайдағы
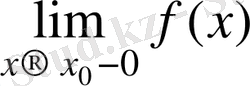 шекті функцияның
сол жақты шегі
деп атайды. Дәл осылайша функцияның
оң жақты
шекті функцияның
сол жақты шегі
деп атайды. Дәл осылайша функцияның
оң жақты
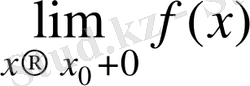 шегі де анықталады. Функцияның сол жақты және оң жақты шектерін
біржақты шектер
дейді.
шегі де анықталады. Функцияның сол жақты және оң жақты шектерін
біржақты шектер
дейді.
Енді үзіліс түрлерін ажыратайық.
Анықтама.
Функцияның
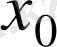 нүктесінде өз-ара тең емес ақырлы біржақты шектері бар болса,
нүктесінде өз-ара тең емес ақырлы біржақты шектері бар болса,
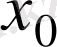 нүктесі функцияның
І-текті үзіліс нүктесі
деп аталады. Кейде оны ақырлы секіріс деп
(10а-сурет)
атайды.
нүктесі функцияның
І-текті үзіліс нүктесі
деп аталады. Кейде оны ақырлы секіріс деп
(10а-сурет)
атайды.
Анықтама.
Функцияның
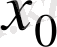 нүктесіндегі ақырлы біржақты шектердің ең болмағанда біреуі жоқ болса,
нүктесіндегі ақырлы біржақты шектердің ең болмағанда біреуі жоқ болса,
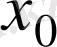 нүктесі функцияның
ІІ-текті үзіліс нүктесі
деп аталады
(10б-сурет)
.
нүктесі функцияның
ІІ-текті үзіліс нүктесі
деп аталады
(10б-сурет)
.
Мысал.
а)
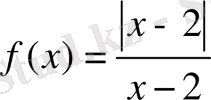 функциясы
функциясы
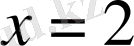 нүктесінде үзіліссіздікке зертте.
нүктесінде үзіліссіздікке зертте.
Шешуі.
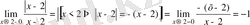
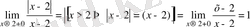 ,
,
яғни сол жақты шегі -1, ал оң жақты шегі 1, ақырлы сандар, өз-ара тең емес, олай болса
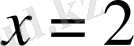 нүктесі І-текті үзіліс нүктесі болады (10а-сурет) .
нүктесі І-текті үзіліс нүктесі болады (10а-сурет) .
б)
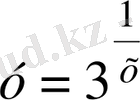 функциясын үзіліссіздікке зертте.
функциясын үзіліссіздікке зертте.
Шешуі
. Функция
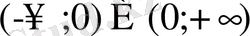 аралығында анықталған.
аралығында анықталған.
 нүктесіндегі біржақты шектерді табайық.
нүктесіндегі біржақты шектерді табайық.
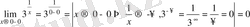
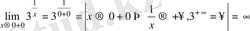 ,
,
яғни сол жақты шегі 0, ал оң жақты шегі шексіздік. Олай болса
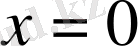 нүктесі ІІ-текті үзіліс нүктесі болады (10б-сурет) .
нүктесі ІІ-текті үзіліс нүктесі болады (10б-сурет) .
в)
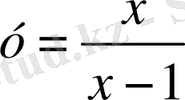 функциясын үзіліссіздікке зертте.
функциясын үзіліссіздікке зертте.
Шешуі.
Функция
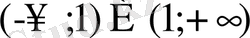 аралығында анықталған.
аралығында анықталған.
 нүктесіндегі біржақты шектерді табайық.
нүктесіндегі біржақты шектерді табайық.
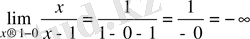
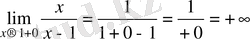 ,
,
яғни сол жақты де, оң жақты шегі де шексіздік. Олай болса
 нүктесі ІІ-текті үзіліс нүктесі болады (10в-сурет) .
нүктесі ІІ-текті үзіліс нүктесі болады (10в-сурет) .
ТЕОРИЯЛЫҚ СҰРАҚТАР
- Функция шегі анықтамасын есіңе түсір.
- Бірінші және екінші тамаша шектер деп қандай шектерді айтамыз?
- Ақырсыз аз функцияларды қалай салыстырады?
- Үзіліссіз функция деп қандай функцияны айтамыз?
- Үзіліс түрлерін анықта.
АЛТЫНШЫ ЛЕКЦИЯ
ТУЫНДЫ
Көп жағдайда функция мәнін білумен қатар аргументтің өзгерісіне байланысты функцияның өзгеру жылдамдығын білу де маңызды болады.
y
=f(x)
функциясын қарастырайық (1-сурет)
.
Осы функция
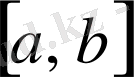 кесіндісінде анықталған және үзіліссіз болсын. Кез келген
кесіндісінде анықталған және үзіліссіз болсын. Кез келген
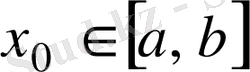 үшін
үшін
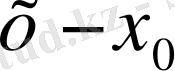 айырма
х
аргументтің
айырма
х
аргументтің
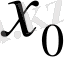 нүктесіндегі
өсімшесі
деп аталады да,
нүктесіндегі
өсімшесі
деп аталады да,
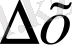 деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен,
=
x =
+
.
Ал
 айырма
f(x)
функциясының
айырма
f(x)
функциясының
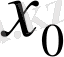 нүктесіндегі
өсімшесі
деп аталады да,
нүктесіндегі
өсімшесі
деп аталады да,
 деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен,
=
=
.
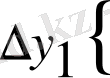
2-суретте көрсетілген
y=f
1
(x
) және
y=f
2
(x)
функцияларды қарастырайық. Аргумент мәні
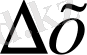 шамаға өзгергенде бұл функциялардың мәндері де белгілі бір шамаға өзгереді. Суретте
f
2
(x)
функцияның мәні
f
1
(x
) функцияға қарағанда көп өзгереді (өседі) .
шамаға өзгергенде бұл функциялардың мәндері де белгілі бір шамаға өзгереді. Суретте
f
2
(x)
функцияның мәні
f
1
(x
) функцияға қарағанда көп өзгереді (өседі) .
Аргумент мәні бірдей шамаға өзгерген кездегі функциялардың өзгерістерін салыстыру үшін функцияның өзгеріс жылдамдығы ұғымын енгізеді. Оны орташа жылдамдық дейді де, функция өзгерісінің аргумент өзгерісіне қатынасымен анықтайды:

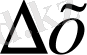
Орташа жылдамдық
х
0
нүктесіне ғана қатысты қарастырылмай, аргумент өзгерісінен де байланысты болады. Функция жылдамдығын аргумент өзгерісінен байланыссыз қарастыру үшін функцияның нүктедегі жылдамдығын қарастырады. Функцияның нүктедегі жылдамдығын анықтау үшін
х
-ті
х
0
аргументке шексіз жақындатады, немесе
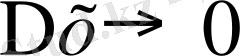 . Осы кезде үзіліссіз функция өзгерісі нолге жақындайды, яғни
. Осы кезде үзіліссіз функция өзгерісі нолге жақындайды, яғни
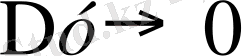 . Нолге шексіз жақындайтын функция өзгерісінің нолге шексіз жақындайтын аргумент өзгерісіне қатынасы функцияның
х
0
нүктедегі өзгеріс жылдамдығын береді. Функцияның
х
0
нүктедегі осы өзгеріс жылдамдығын
f(x)
функциясының
х
0
нүктедегі туындысы деп атайды:
. Нолге шексіз жақындайтын функция өзгерісінің нолге шексіз жақындайтын аргумент өзгерісіне қатынасы функцияның
х
0
нүктедегі өзгеріс жылдамдығын береді. Функцияның
х
0
нүктедегі осы өзгеріс жылдамдығын
f(x)
функциясының
х
0
нүктедегі туындысы деп атайды:
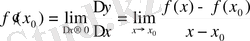 .
.
Сонымен, функция туындысының анықтамасын берейік.
Анықтама.
Функция өсімшесінің аргумент өсімшесіне қатынасының аргумент өсімшесі нолге ұмтылған кездегі шегі
функция туындысы
деп аталады. Әдетте оны
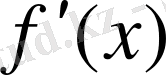 немесе
немесе
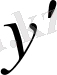 деп белгілейді:
деп белгілейді:
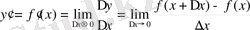 (1)
(1)
Функцияның туындысын алуды - функцияны дифференциалдау дейді.
(а; в) интервалының әрбір нүктесінде туындысы бар функцияны сол интервалда дифференциалданады дейді.
Мынадай тұжырым дұрыс болады: Егер f(x) функцисы х 0 нүктеде дифференциалданса, онда функция х 0 нүктеде үзіліссіз болады.
Бірақ осыған кері тұжырым дұрыс бола бермейді. Мысалы , y= x функциясы x=0 нүктеде үзіліссіз. Бірақ оның x=0 нүктедегі туындысы болмайды. Шынында да, егер бар болса, туындыны мына формуламен табар едік:
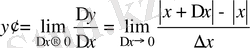 .
.
Ал x=0 нүктеде
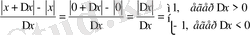
 болғандықтан
болғандықтан
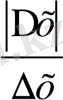 қатынастың шегі болмайды. Шек болмаса туындысы да жоқ.
қатынастың шегі болмайды. Шек болмаса туындысы да жоқ.
Туындының геометриялық мағнасы. y=f(x) функциясы
х
0
нүктесінде дифференциал- дансын. Осы функцияның
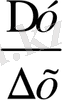 қатынасы
қатынасы
 бұрыштың тангенсіне тең.
бұрыштың тангенсіне тең.
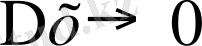 жағдайда
жағдайда
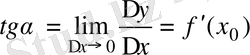 .
.
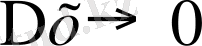 жағдайда М
0
М қима функция графигіне
х
0
нүктесінде жүргізілген жанамаға айналады. Ал
tg
жағдайда М
0
М қима функция графигіне
х
0
нүктесінде жүргізілген жанамаға айналады. Ал
tg
 жанаманың (түзудің) бұрыштық коэффициенті, яғни
жанаманың (түзудің) бұрыштық коэффициенті, яғни
k= tg
 .
.
Сонымен,
туындының геометриялық мағнасы:
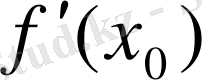 туынды дегеніміз y=f(x) функция графигіне х
0
нүктесінде жүргізілген жанаманың бұрыштық коэффициенті:
туынды дегеніміз y=f(x) функция графигіне х
0
нүктесінде жүргізілген жанаманың бұрыштық коэффициенті:
k= tg
 =
=
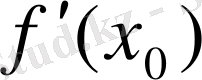 (2)
(2)
Сонда y=f(x) функция графигіне х 0 нүктесінде жүргізілген жанама теңдеуі мынадай түрде жазылады:
у -
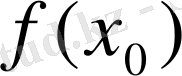 =
=
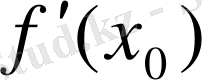 (x-x
0
)
(3)
(x-x
0
)
(3)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz