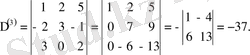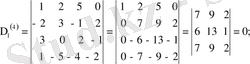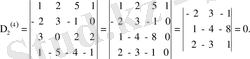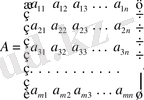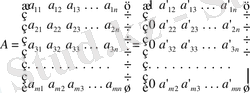Біртекті сызықтық теңдеулер системалары

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

Қазақстан Республикасы Білім және ғылым
министрлігі Ы.Алтынсарин атындағы Арқалық
мемлекеттік педагогикалық институты

Жаратылыстану және ақпараттандыру факультеті

Тақырыбы:
Матрицаның (векторлар системасының) рангісі және оны есептеу.
Rп кеңістіктегі п векторлардың сызықтық
тәуелсіз (тәуелді) болуының қажетті
және жеткілікті шарты.
Кронекер – Капелли теоремасы.
Біртекті сызықтық теңдеулер системалары.

Орындаған: И-21 тобының студенті
Дюсембекова А.

Тексерген: Сабитбекова Г.С.

Арқалық, 2008жыл.

Жоспар:

1) Матрицаның (векторлар системасының) рангісі және оны есептеу.

2) Rп кеңістіктегі п векторлардың сызықтық тәуелсіз (тәуелді) болуының
қажетті және жеткілікті шарты.

3) Кронекер – Капелли теоремасы.

4) Біртекті сызықтық теңдеулер системалары.

Матрицаның (векторлар системасының) рангісі және оны есептеу. Айталық,
өлшемдері болатын қайсыбір матрица берілген болсын. Осы
матрицаның қалауымызша алынған k жолдары мен k бағандарының қиылысуында
орналасқан аij элементтерден құралған анықтауыш A матрицаның k -сыншы ретті
миноры деп аталады және деп белгіленеді. А матрицаның элементтерінің
өздерін бірінші ретті минорлар деп атайды.
1-анықтама. Нольдік емес А матрицаның рангісі деп А матрицаның
ең болмағанда нольден өзгеше r-інші ретті бір миноры бар
болатындай, ал қалған (r+1)-інші және одан жоғары ретті барлық
минорлары нольге тең болатындай r санын айтады.
Нольдік емес кез келген А матрицаның ең болмағанда нольден өзге бір
элементі бар болады (бірінші ретті минор). Сондықтан А матрицаның r рангісі
бірден кем болмайды. Сондай-ақ осы матрица элементтерінен реттілігі т мен п
екі санның кішісінен жоғары болатын минорлар құрастыруға болмайды. Олай
болса, r саны (матрица рангісі) 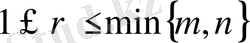теңсіздігін қанағаттандырады.
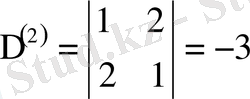
1-мысал. Мына матрицаның
рангісін есептегі шығару керек.
Алынған матрицаның нольден өзгеше екінші дәрежелері миноры бар болады

3-інші ретті минорлардың барлығы да (ондайлар төртеу) нольге тең:

Алынған матрицаның реттілігі бұдан жоғары минорлары болмайды. Олай болса,
бұл матрицаның рангісі r =2.
1 - анықтама бойынша матрица рангісін тапқанда есептеуге тура келетін
минорлардың саны едәуір көп болады. Мына келесі ескертуге (ережеге)
сүйеніп, ол есептеулерді біршама ықшамдауға болады.
Рангіні есептеу е р е ж е с і: матрицаның рангісін есептегенде
реттілігі төмен минорлардан реттілігі жоғары минорларға көшіп
отыру жөн; сонда егер нольден өзгеше k-сыншы ретті минор
табылған болса, онда тек минорларды айнала қоршап жиектеуші
(k+1)-інші ретті минорларды ғана есептеу қажет болады. (k+1)-
інші ретті жиектеуші минорлардың барлығы нольге тең болатын
жағдайда матрицаның рангісі k -ға тең болады.
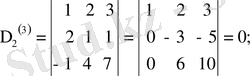
2-мысал. Мына матрицаның
рангісін есептеу керек.
Алынған матрицаның сол жақ жоғарғы бұрышында тұрған екінші ретті минор
нольден өзгеше

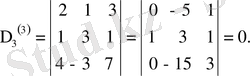
Сондай-ақ оны ж и е к т е у ш і үшінші ретті минор да нольден өзгеше

Алайда 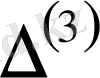минорды жиектеуші төртінші ретті екі минор да нольге тең

Олай болса, алынған матрицаның рангісі r =3.
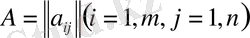Айталық өлшемдері матрицаның рангісі r-ге тең болсын.
Нольден өзгеше r-інші ретті минор А матрицаның б а з и с т і к м и н о р
ы деп, ал осы минордың жолдары мен бағандары базистік деп аталады. Келесі
негізгі теорема тура.
1-теорема. (базистік минор жайлы). Базистік жолдар (базистік жолдар)
сызықтық тәуелді емес. А матрицаның кез келген жолы (кез келген бағаны)
базистік жолдардың (базистік бағандардың) сызықтық комбинациясы болып
табылады.
Теореманың дәлелдемесін матрицаның жолдары үшін орындаймыз (бағандар
үшін оысған ұқсас түрде дәлелденеді).
Айталық, қарсы жорып, базистік жолдар сызықтық тәуелді дейік, онда осы
жолдардың бірі қалғандарының сызықтық комбинациясы болып табылады. Енді осы
жолдан сол аталған сызықтық комбинацияны шегерсек, онда анықтауыштардың
қаситеі бойынша базистік минордың мәні өзгермейді, ал мұнымен қоса, ол тік
минордың мәні өзгермейді, ал мұнымен қоса, ол жолдардың бірі ылғи
нольдерден құралатын болып шығады, сондықтан да минордың өзі де нольге тең
болады. Ал мұның өзі базистік минор анықтамасына қайшы келеді. Ендеше,
базистік жолдар сызықтық тәуелсіз болғаны.
Енді А матрицаның қай жолы да оның базистік жолдарының сызықтық
комбинациясы екендігін дәлелдейік.
Өзіміз білетіндей, жолдардың (бағандардың) орнын қалауымызша
өзгерткенде анықтауыш нольге тең болу қасиетін сақтап қалады. Сондықтан,
жалпылыққа нұқсан келтірмей-ақ, базистік минор А матрицаның сол жақ
жоғарғы бұрышында, яғни алғашқы r жолдарда және алғашқы r бағандарда жатады
деуге болады. Енді, айталық, k мен s қалауымызша алынған натурал сандар да,
олар мына 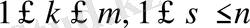теңсіздіктерді қанағаттандырады дейік. Сонда келесі
анықтауыштың

(14)
нольге тең болатындығына көз жеткіземіз.
Шынында да, егер 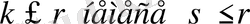болса, онда (14) анықтауыш нольге тең болады,
өйткені оның екі жолы не екі бағаны бірдей болып отыр. Ал егерде kr және
sr болса, онда аталған анықтауыш матрицаның (r+1)- інші ретті миноры болып
шығады, ал мұндай минордың қай-қайсысы да нольге тең (базистік минордың
анықтамасы бойынша). Олай болса, k-ның 1-ден m-ге дейінгі және s-тің 1-ден
n-ге дейінгі барлық мәндерінде (14) анықтауыш нольге тең болады.
(14) анықтауыштың соңғы бағаны элементтерінің s нөміріне тәуелсіз
алгебралық толықтауыштарын былай белгілейік:

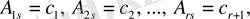
сонымен бірге оны соңғы бағанның элементтері бойынша жіктейік. Сонда 1-
ден n-ге дейінгі әрбір s үшін мына теңдік орындалады.
(15)
(15) теңдікте коэффициент cr+1=Aks0, өйткені ол базистік минормен дәл
бірдей. Егер (15) теңдікті 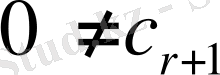коэффициентке бөліп және де мына
белгілеулерді 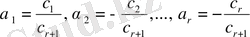енгізсек, онда 1-ден n-ге дейінгі барлық s үшін мынау
табылады
(16)
(16) теңідік болса, k-сыншы жолдың 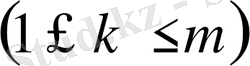алдыңғы (базисік) r жолдардың
сызықтық комбинациясы екендігін білдіреді.
Өзіміз алдыңғы айтылғаннан білетініміздей, өлшемдері болатын А
матрицаны әрқайсысы n өлшемді векторлардың (осы мартица жолдарының)
системасы ретінде қарасрытуға болады. Сонда матрица жолдарының немесе
бағандарының сызықтық тәуелді (тәуелсіз) болуы сәкес векторлар системесының
сызықтық тәуелді (тәуелсіз) болатындығын білдіреді. 1-теоремадан матрица
рангісі мен векторлар системасы рангісі арасындағы байланыс салдар ретінде
шығады.
С а л д а р. А матрицаның рангісі r осы матрицаның жолдары (бағандары)

құрайтын векторлар системасының рангісімен дәл бірдей
болады.
Шынында да, А матрицаның жолдары құрайтын векторлар системасын
қарастырайық. 1-теорема бойынша осы матрицаның әрбір жолы оның сызықтық
тәуелсіз базистік r жолдарының сызықтық комбинациясы болып табылады. Ал
мұның өзі базистік жолдардың қарастырылып отырған векторлар системасының
базисін құрайтынын білдіреді. Осы сияқты, А матрицаның сызықтық тәуелсіз
базистік r бағандардың басқа векторлар (бағандар) системасыньщ базисін
құрайтындығы тағайындалады. Олай болса, векторлардың осы аталған екі
системасының да бірдей r рангісі А матрицаның рангісімен дәл бірдей
болады. Осы айтылғанға қарағанда, матрица рангісін жолдар (бағандар)
системасының рангісі, яғни сызыктық тәуелсіз жолдардың (бағандардың)
барынша үлкен саны, ретінде анықтауға болады екен.
Сол салдарды ескере отырып, матрицаның немесе векторлар системасының
рангісін есептеу үшін элементар түрлендірулерді қолданып орындалатын басқа
тәсілді қарастырамыз. Матрицаны элементар түрлендірулер деген (векторлар
системасы жағдайына ұқсас) мыналар
1) матрицаның жолдарын (бағандарын) ауыстырып қою;
2) тұтастай нольдерден тұратын жолды(бағанды) сызып тастау;
3) кез келген жолдың барлық элементтерін нольден
өзге санға көбейту;
4) кез келген жолдың элементтеріне басқа бір жолдың нолъден өзге санға
көбейтілген сәйкес элементтерін қосу.
Келесі ұйғарым тура: элементар түрлендірулер орындалғанда матрица
рангісі өзгермейді. Егер матрицаны векторлардың (жолдардың немесе
бағандардың) системасы ретінде қарастырып және де векторлар системасының
рангісі өзгермейтіні жайлы сәйкес теореманы ескеретін болсақ, бұл ұйғарымды
арнайы дәлелдеудің қажеті болмай шығады. Рангісі бірдей А мен В екі матрица
б а р а б а р делінеді және былай А~В белгіленеді.
Осы айтылған тәсілдің мәнісі мынау: алынған матрицаны онымен барабар,
ал рангісі оның түріне қарап та оңай тағайындалатын матрицаға түрлендіру.
Ондайларға, мысалы, диагональ түрдегі матрицалар жатады. Өлшемдері
болатын А = aij матрица, егер оның а11, а22, . . . аrr (r=mіn{m,n})
диагональдық элементтерінен өзге барлық элементтері нольге тең болса, оны
диагональ түрдегі матрица деп атайды. Ондай матрицаның рангісі r -ге тең
екендігі айқын. Енді қажетті түрлендірулердің орындалу ретін толығырақ
қарастырайық.
Айталық, алынған мына матрицаның

анықтық үшін тп деп алайық (өйтпегенде жолдарды бағандармен алмастырып
аламыз). Енді осы матрицаның, әрбір бағанын бірлік бағанға келтіре отырып,
оның жолдарын элементар түрлендіретін боламыз.
Айталық, 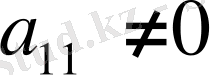болсын (егер а11=0 болса, онда а11 орнында нольдік емес
элемент тұратындай етіп жолдар мен бағандардың орындарын алмастырамыз), оны
басты элемент деп атап, айнала қоршап қоямыз. Енді басты элемент тұрған жол
мен бағанды сәйкесінше басты жол және басты баған дейтін боламыз. Ал енді
бірінші (басты) жолды 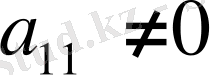элементке бөлеміз, бұдан кейін бірінші жолдағы
бірінші элемент бірге тең болып шығады. Әрі қарай түрлендірілген бірінші
жолды тізбектей мына элементтерге а21, а31,...,аm1 көбейтіп және екінші,
үшінші, ..., m-інші жолдардан сәйкесшше шегергенде бірінші бағанның,
екіншіден бастап, барлық элементгері ноль болып шығады. Нәтижеде, А матрица
өзімен барабар жаңа матрицаға түрленеді, ал жазылуы былай

мұндағы штрихпен жазылған элементтер жаңа матрицанікі.
Енді екінші бағанды бірлік бағанға келтіреміз. Егер элемент
болса, оны басты элемент деп қабылдап, алдыңғыдағыға ұқсас түрде оның
орнында бірді шығарып аламыз, ал екінші бағанның қалған барлық
элементтерін нольге айналдырамыз.
Егер болса, орнында нольдік емес элемент шығатындай ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.